Robust squeezed light against mode mismatch using a self imaging optical parametric oscillator

ABSTRACT We present squeezed light that is robust against spatial mode mismatch (beam displacement, tilt, and beam-size difference), which is generated from a self-imaging optical parametric

oscillator below the threshold. We investigate the quantum properties of the generated light when the oscillator is detuned from the ideal self-imaging condition for stable operation. We

find that the generated light is more robust to mode mismatch than single-mode squeezed light having the same squeezing level, and it even outperforms the single-mode infinitely squeezed

light as the strength of mode mismatch increases. SIMILAR CONTENT BEING VIEWED BY OTHERS GENERATION OF TWO MODE MECHANICAL SQUEEZING INDUCED BY NONDEGENERATE PARAMETRIC AMPLIFICATION Article

Open access 08 November 2024 STRUCTURED LIGHT ANALOGY OF QUANTUM SQUEEZED STATES Article Open access 21 October 2024 OVERCOMING DETECTION LOSS AND NOISE IN SQUEEZING-BASED OPTICAL SENSING

Article Open access 12 May 2021 INTRODUCTION Squeezed light is a versatile quantum resource for quantum information technologies1,2,3,4,5,6,7. In particular, in quantum metrology, it reduces

noises in measurement below the standard quantum limit8,9,10; a notable application is gravitational wave detectors11,12. The quality of squeezed light is typically measured by the

squeezing level (the degree of noise reduction compared with the vacuum noise), which is reported up to 15 dB by using an optical parametric oscillator (OPO)13. To exploit the full potential

of squeezed light in quantum technologies, however, a precise mode matching with subsequent operations is required14,15,16. Mismatch of modes results in a loss of original properties of

light, e.g. degradation of the squeezing level15. For classical light, mode mismatch is not a critical issue because the loss of light can be simply compensated by means of increasing the

optical power. However, for squeezed light, there is a limit on compensation by increasing the initial squeezing level, e.g., if the mode matching efficiency is less than 50%, there is no

way to obtain more than 3 dB squeezing. Moreover, if mode mismatch varies dynamically or even fluctuates stochastically, its correction is a very challenging problem14,17. A way of

circumventing this problem is to prepare squeezed light in a few additional modes, so that, in case of mode mismatch, squeezed light from the additional modes is coupled into a target

mode18,19. Recently, such an idea is demonstrated by employing an additional OPO operating in a Hermite–Gaussian \({\hbox{HG}}_{{01}}\) mode for a vertical mode mismatch16. However, to be

robust against more general and stronger mode mismatch, it is required to build many phase-locked OPOs, each operating in a different \({\hbox{HG}}_{{mn}}\) mode20, which is technically

demanding. Here we show that a single OPO in a self-imaging configuration can generate squeezed light that is robust against various cases of mode mismatch. The self-imaging OPO is based on

a fully degenerate optical cavity in spatial modes, called a self-imaging cavity21,22, hence it can support spatially multimode quantum states generated by a parametric down-conversion

process23,24,25. However, the ideal self-imaging condition leads to cavity instability, and thus, a small detuning is necessary for stable operation22. In this work, we characterize the

quantum properties of the light from a self-imaging OPO with a small detuning (parametrized by the Gouy phase shift) and an intracavity loss, and we find that squeezed vacua at multiple

\({\hbox{HG}}_{{mn}}\) modes are simultaneously generated without much degradation from the ideal self-imaging condition. We then investigate the injection of the generated multimode light

into a target mode in the presence of mode mismatch (beam displacement, tilt, and beam-size difference both for horizontal and vertical directions) and optical losses. We find that the

multimode squeezed light is more robust to mode mismatch than single-mode squeezed light with the same squeezing level, and at sufficiently large mode mismatch, it even outperforms the

single-mode infinitely squeezed light. Such robustness to mode mismatch can be achieved in a detuning range of a self-imaging OPO within reach of the experimental control. QUANTUM PROPERTIES

OF MULTIMODE SQUEEZED LIGHT SPATIAL PROPERTIES OF PARAMETRIC DOWN CONVERSION To generate squeezed light, we consider a degenerate type-I parametric down conversion in a \(\chi

^{(2)}\)nonlinear crystal in the low gain regime26. The interaction Hamiltonian can be described as $$\begin{aligned} {\hat{H}} = -{i\hbar{g} \over 2} \int d^{2}{\vec{q}}_{s}

d^{2}{\vec{q}}_{i}\, {\tilde{K}}({\vec{q}}_{s},{\vec{q}}_{i}) \, {\hat{a}}^{\dagger }({\vec{q}}_{s}) {\hat{a}}^{\dagger }({\vec{q}}_{i})+h.c., \end{aligned}$$ (1) where \({\vec{q}}_{s(i)}\)

is the transverse component of the wave vector for the signal (idler) field, \({\hat{a}}^{\dagger }({\vec{q}})\) is the creation operator at \({\vec{q}}\) and \(t=0\), and _g_ is the gain

parameter proportional to the crystal nonlinearity \(\chi ^{(2)}\), the length of the nonlinear crystal \(l_{c}\), and the maximum pump amplitude \(A_{p}\). The kernel

\(K({\vec{q}}_{s},{\vec{q}}_{i})\) determines the spatial properties of the generated light, which depends on the pump beam distribution and the phase matching condition. For a monochromatic

Gaussian pump beam focused at the center of the crystal, the kernel is given by23, 27 $$\begin{aligned} {\tilde{K}}({\vec{q}}_{s},{\vec{q}}_{i})&= \exp \left( {-{w_{p}^{2} \over 4}\vert

{\vec{q}}_{s}+{\vec{q}}_{i} \vert ^{2}} \right) {\text{sinc}}\left( {l_{c} \over 4k_{p}} \left| {\vec{q}}_{s} - {\vec{q}}_{i} \right| ^{2} \right) , \end{aligned}$$ (2) where \(k_{p}\) and

\(w_{p}\) are the wavenumber and the waist of the pump beam, respectively. The Gaussian function originates from the pump distribution (making the anticorrelation between \({\vec{q}}_{s}\)

and \({\vec{q}}_{i}\)), and the sinc function is by the phase matching condition (making the correlation between \({\vec{q}}_{s}\) and \({\vec{q}}_{i}\)). The Hamiltonian \({\hat{H}}\) in

Eq. (1) can be described by the transverse position operator \({\hat{a}}^\dagger ({\vec{x}}) (= {1 \over 2\pi } \int d^{2}{\vec{q}}\, e^{{-i{\vec{q}}} \cdot {\vec{x}}}\,{\hat{a}}^{\dagger

}({\vec{q}}))\) as well, using the inverse Fourier transform, $$\begin{aligned} {\hat{H}} = -{i\hbar{g} \over 2} \int d^{2}{\vec{x}}_{s} d^{2}{\vec{x}}_{i}\, K({\vec{x}}_{s},{\vec{x}}_{i})

\, {\hat{a}}^{\dagger }({\vec{x}}_{s}) {\hat{a}}^{\dagger }({\vec{x}}_{i})+h.c. \end{aligned}$$ (3) The associated kernel \(K({\vec{x}}_{s},{\vec{x}}_{i})\) is decomposed with

\({\hbox{HG}}_{{mn}}\) functions (\(\psi ^H_{mn}(x,y)\)) by approximating the sinc function in \({\tilde{K}}({\vec{q}}_{s},{\vec{q}}_{i})\) to the Gaussian function (\({\mathrm{sinc}}(x^{2})

\approx \exp (-\alpha x^{2})\))28,29, $$\begin{aligned} K({\vec{x}}_{s},{\vec{x}}_{i}) = \sum _{m,n=0}^{\infty }\mu ^{m+n}\, \psi ^H_{mn}({\vec{x}}_{s}) \,\psi ^H_{mn}({\vec{x}}_{i}),

\end{aligned}$$ (4) where $$\begin{aligned} \psi ^H_{mn}(x,y)&= { \exp \left( -{{ x^{2}+ y^{2}} \over w_{H}^{2} }\right) H_m\left( {\sqrt{2} x \over w_{H} }\right) H_n\left( { \sqrt{2} y

\over w_{H} }\right) \over {w_{H} \sqrt{2^{m+n-1} \pi m!n!}} } \nonumber \\ \mu&= {1 - \sqrt{\xi } \over 1+\sqrt{\xi }} \nonumber \\ \xi&= \alpha l_{c}/2z_{p} \nonumber \\

w_{H}&= \sqrt{2} \xi ^{1/4} w_{p}. \end{aligned}$$ (5) The pump beam property has been expressed in terms of the Rayleigh range \(z_{p}= k_{p} w_{p}^{2}/2\), and \(H_n(x)\) is the _n_-th

order Hermite polynomial. The key parameters determining the kernel are a modified (by \(\alpha\)) focusing parameter of the pump \(\xi\) and the waist size \(w_{H}\). \(\xi\) determines

the eigenvalues \(\mu ^{m+n}\), where \(\left| {\mu }\right| ^{m+n} < 1\), and \(w_{H}\) determines the width of HG modes \(\psi ^H_{mn}(x,y)\). The Schmidt number _M_, quantifying the

average number of modes30, can be also expressed as a function of the focusing parameter \(\xi\), $$\begin{aligned} M = {1 \over 4} \left( \sqrt{\xi }+\sqrt{1/\xi }\right) ^{2}.

\end{aligned}$$ (6) _M_ has the minimum value of one at \(\xi =1\), and _M_ increases as \(\xi\) deviates from one. With this kernel decomposition, the Hamiltonian in Eq. (3) can be

expressed in a decoupled form $$\begin{aligned} {\hat{H}} = -{i\hbar g \over 2} \sum _{mn} \mu ^{m+n} \left( {\hat{A}}^{H}_{mn}\right) ^{\dagger }\left( {\hat{A}}^{H}_{mn}\right) ^{\dagger }

+ h.c., \end{aligned}$$ (7) where $$\begin{aligned} \left( {\hat{A}}^{H}_{mn}\right) ^{\dagger } = \int d^{2}{\vec{x}} \, \psi ^H_{mn}({\vec{x}}) \, {\hat{a}}^{\dagger } ({\vec{x}})

\end{aligned}$$ (8) are the creation operators of the eigenmodes of the interaction Hamiltonian, which are in the \({\text{HG}}_{mn}\) modes \(\psi ^H_{mn}({\vec{x}})\). The operators

satisfy the bosonic commutation relation \([{\hat{A}}^{H}_{mn},\left( {\hat{A}}^{H}_{kl}\right) ^{\dagger }] = \delta _{mn,kl}\), constructing an orthonormal HG mode basis. Note that the

Hamiltonian is a direct sum of \(\left( {\hat{A}}^{H}_{mn}\right) ^{\dagger }\left( {\hat{A}}^{H}_{mn}\right) ^{\dagger } + {\hat{A}}^{H}_{mn} {\hat{A}}^{H}_{mn}\) from different

\({\hbox{HG}}_{{mn}}\) modes, which means that it generates squeezed light in each of the multiple spatial modes. The eigenvalues \(\mu ^{m+n}\) are associated with the relative squeezing

levels in different modes, which will be discussed in the following section. SELF-IMAGING OPO Let us construct a cavity that is compatible with the spatially multimode Hamiltonian in Eq. 

(7). While a typical cavity resonates on a single \({\hbox{HG}}_{{00}}\) mode13, for our purpose, we require a degenerate cavity resonant on all \({\hbox{HG}}_{{mn}}\) modes. The cavity

degeneracy is determined by the Gouy phase shift (\(\theta _{G}\)) accumulated by the \({\hbox{HG}}_{{00}}\) mode along one cavity round-trip31,32. A confocal cavity has \(\theta _{G}=\pi \,

{\mathrm{mod}}(2\pi )\), which is resonant only on half of \({\hbox{HG}}_{{mn}}\) modes having either an even or an odd number of \(m+n\)18. On the other hand, a self-imaging cavity

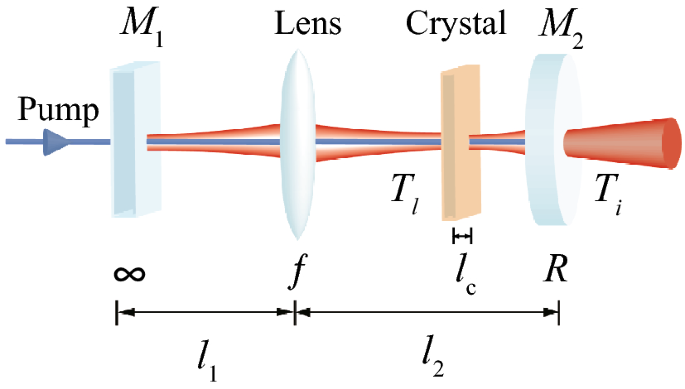
exhibits \(\theta _{G}=0 \, {\mathrm{mod}}(2\pi )\): it is a fully resonant cavity for all \({\hbox{HG}}_{{mn}}\) modes21,22. Figure 1 describes a self-imaging OPO, which consists of a plane

mirror \(M_{1}\), a lens of focal length _f_, a nonlinear crystal of length \(l_{c}\), and a curved mirror \(M_{2}\) of a radius of curvature _R_. The lengths \(l_{1}\) and \(l_{2}\) can be

expressed as $$\begin{aligned} l_{1}&= f+f^{2}/R+\Delta l_{1} \nonumber \\ l_{2}&= f+R+\Delta l_{2}. \end{aligned}$$ (9) When \(\Delta l_{1} = \Delta l_{2} = 0\), the OPO becomes

fully degenerate for all \({\hbox{HG}}_{{mn}}\) modes. This ideal condition, however, leads to cavity instability22, and thus, small detunings (\(\Delta l_{1}, \Delta l_{2}\)) are required

for stable operation. The Gouy phase shift with such a detuning is $$\begin{aligned} \theta _{G} = \cos ^{-1} \left( 1 + 2 {\Delta l_{2} \over R} \left( {\Delta l_{1} \over R} + {\Delta

l_{2} \over R} - {\Delta l_{1} \over R} {\Delta l_{2} \over R} \right) \right) , \end{aligned}$$ (10) where we have assumed \(f=R\). As a result, when the cavity is locked for

\({\hbox{HG}}_{{00}}\) mode, a high-order \({\hbox{HG}}_{{mn}}\) mode attains a phase shift of \((m+n)\theta _{G}\)31. The cavity has HG eigenmodes $$\begin{aligned} \psi _{mn}(x,y) = {\exp

\left( -{x^{2}+y^{2} \over w_{c}^{2}}\right) H_m \left( {\sqrt{2}x \over w_{c}}\right) H_n\left( {\sqrt{2}y \over w_{c}}\right) \over w_{c} \sqrt{2^{m+n-1}\pi m! n!}} \end{aligned}$$ (11)

with the waist size of \(w_{c} = \sqrt{R\lambda _0/2\pi }\) (\(\lambda _0\): the free space wavelength) for small detunings \(\Delta l_{1}, \Delta l_{2} \ll R\), and the associated creation

operators are $$\begin{aligned} {\hat{A}}_{mn}^\dagger = \int d^{2}{\vec{x}} \, \psi _{mn}({\vec{x}}) \, {\hat{a}}^{\dagger } ({\vec{x}}). \end{aligned}$$ (12) To match the cavity modes with

the eigenmodes of the Hamiltonian in Eq. (4), we position the crystal at the cavity waist and set \(R=2\pi w_{H}^{2} / \lambda _0\), while a more general case of mismatch between the modes

will be discussed in “Effect of mode mismatch inside the OPO” section. In this configuration, we obtain a decoupled quantum-Langevin-equation for each \({\hat{A}}_{mn}\)33, $$\begin{aligned}

{d \over dt}{\hat{A}}_{mn}(t) = {1 \over i\hbar }[{\hat{A}}_{mn}(t),{\hat{H}}] -\left( \gamma _{i}+\gamma _{l}-i\Delta _{mn}\right) {\hat{A}}_{mn}(t) +\sqrt{2\gamma _{i}}{\hat{A}}^i_{mn}(t)

+ \sqrt{2{\gamma }_{l}} {\hat{A}}_{mn}^l (t), \end{aligned}$$ (13) where \({\hat{A}}_{mn}^i\) and \({\hat{A}}_{mn}^l\) are the annihilation operators of the input and the intra-cavity loss

modes, respectively, and the corresponding decay rates are given by \(\gamma _{i}=T_{i}/2\tau\) and \(\gamma _{l} = T_{l}/2\tau\) (\(T_{i}\) and \(T_{l}\) are shown in Fig. 1, \(\tau\): the

round trip time). As we consider a cavity locked for the \({\hbox{HG}}_{{00}}\) mode, the cavity detuning frequency of \({\hbox{HG}}_{{mn}}\) mode, \(\Delta _{mn}\), is given by

\((m+n)\theta _{G}/\tau\). We have used the approximation \(T_{i}, T_{l}, \theta _{G} \ll 1\). Using Eq. (7), $$\begin{aligned} {1 \over i\hbar }[{\hat{A}}_{mn}(t),{\hat{H}}] = -g \mu ^{m+n}

{\hat{A}}_{mn}^{\dagger }(t), \end{aligned}$$ (14) and then, the Fourier transform of Eq. (13) becomes $$\begin{aligned} (\gamma _{i}+\gamma _{l}-i\omega -i\Delta _{mn})

{\hat{A}}_{mn}(\omega ) + g \mu ^{m+n} {\hat{A}}^{\dagger }_{mn}(-\omega ) = \sqrt{2\gamma _{i}}{\hat{A}}^{i}_{mn}(\omega ) +\sqrt{2\gamma _{l}}{\hat{A}}^l_{mn}(\omega ) \end{aligned}$$ (15)

at frequency \(\omega\). To investigate quantum correlations of the generated light at sidebands frequency \(\omega\), we employ a vector of quadrature operators in \({\hbox{HG}}_{{mn}}\)

modes, $$\begin{aligned} {\hat{\mathbf{Q}}}(\omega ) = [{\hat{X}}_{00}(\omega ),{\hat{X}}_{01}(\omega ),\ldots ,{\hat{P}}_{00}(\omega ),{\hat{P}}_{01}(\omega ),\ldots ]^T, \end{aligned}$$

(16) where \({\hat{X}}_{mn}(\omega ) = {\hat{A}}_{mn}(\omega )+{\hat{A}}_{mn}^{\dagger }(-\omega )\) and \({\hat{P}}_{mn}(\omega ) = ({\hat{A}}_{mn}(\omega )-{\hat{A}}_{mn}^{\dagger

}(-\omega ))/i\). Express Eq. (15) with this vector operator as $$\begin{aligned} {\mathbf{M}}(\omega ){\hat{\mathbf{Q}}}(\omega ) = \sqrt{2\gamma _{i}}{\hat{\mathbf{Q}}}^{i}(\omega )

+\sqrt{2\gamma _{l}} {\hat{\mathbf{Q}}}^{l}(\omega ) \end{aligned}$$ (17) with $$\begin{aligned} {\mathbf{M}}(\omega ) = \left[ \begin{matrix} (\gamma _{i}+\gamma _{l} -i\omega ){\mathbf{I}}

+ {\mathbf{G}} &{} \quad {\mathbf{D}} \\ -{\mathbf{D}} &{}\quad (\gamma _{i}+\gamma _{l} -i\omega ){\mathbf{I}} - {\mathbf{G}}\\ \end{matrix} \right] , \end{aligned}$$ (18) where

\({\mathbf{I}}_{kl,mn}=\delta _{kl,mn}, {\mathbf{G}}_{kl,mn} = g\mu ^{k+l}\,\delta _{kl,mn}, {\mathbf{D}}_{kl,mn} = \Delta _{kl}\,\delta _{kl,mn}\). Using the input–output relation at the

coupler \({\hat{\mathbf{Q}}}^i+{\hat{\mathbf{Q}}}^o = \sqrt{2\gamma _{i}}{\hat{\mathbf{Q}}}\) (\({\hat{\mathbf{Q}}}^i\) and \({\hat{\mathbf{Q}}}^o\) are the quadrature vectors of input and

output modes), Eq. (17) becomes $$\begin{aligned} {\hat{\mathbf{Q}}}^o(\omega )=(2\gamma _{i}{\mathbf{M}}^{-1}(\omega )-{\mathbf{I}}){\hat{\mathbf{Q}}}^i(\omega )+2\sqrt{\gamma _{i} \gamma

_{l}}{\mathbf{M}}^{-1}(\omega ){\hat{\mathbf{Q}}}^l(\omega ). \end{aligned}$$ (19) As the input is the vacuum state, we obtain the covariance matrix generated from the OPO as follows

$$\begin{aligned} {\mathbf{V}}(\omega ) = 4\gamma _{i} \gamma _{l} {\mathbf{M}}^{-1}(\omega )({\mathbf{M}}^{-1}(-\omega ))^T + (2\gamma _{i}{\mathbf{M}}^{-1}(\omega )-{\mathbf{I}})(2\gamma

_{i}{\mathbf{M}}^{-1}(-\omega )-{\mathbf{I}})^T. \end{aligned}$$ (20) Note that the covariance matrix \({\mathbf{V}}(\omega )\) does not exhibit any coupling between different

\({\hbox{HG}}_{{mn}}\) modes. We can therefore characterize it by considering each \({\hbox{HG}}_{{mn}}\) mode individually. The quantum state in each \({\hbox{HG}}_{{mn}}\) mode turns out

to be a squeezed vacuum aligned with rotated quadratures \({\hat{X}}_{mn}^{(\Theta )}(\omega ), {\hat{P}}_{mn}^{(\Theta )}(\omega )\): $$\begin{aligned} {\hat{X}}_{mn}^{(\Theta )}(\omega

)&={\hat{X}}_{mn}(\omega ) \cos \Theta + {\hat{P}}_{mn}(\omega ) \sin \Theta \nonumber \\ {\hat{P}}_{mn}^{(\Theta )}(\omega )&= - {\hat{X}}_{mn}(\omega ) \sin \Theta +

{\hat{P}}_{mn}(\omega ) \cos \Theta \nonumber \\ \langle \Delta ^{2} {\hat{X}}_{mn}^{(\Theta )}(\omega )\rangle&= 1 - \eta { {4 \left| {{\tilde{g}}_{mn}}\right| } \over { 2 \left|

{{\tilde{g}}_{mn}}\right| + \sqrt{({\tilde{\omega }}^{2}-{\tilde{\Delta }}_{mn}^{2}+{\tilde{g}}_{mn}^{2}+1)^{2} +4 {\tilde{\Delta }}_{mn}^{2}}}} \nonumber \\ \langle \Delta ^{2}

{\hat{P}}_{mn}^{(\Theta )}(\omega )\rangle&= 1 - \eta { {4 \left| {{\tilde{g}}_{mn}}\right| } \over { 2 \left| {{\tilde{g}}_{mn}}\right| - \sqrt{({\tilde{\omega }}^{2}-{\tilde{\Delta

}}_{mn}^{2}+{\tilde{g}}_{mn}^{2}+1)^{2} +4 {\tilde{\Delta }}_{mn}^{2}}}} \nonumber \\ \langle \{ \Delta {\hat{X}}_{mn}^{(\Theta )}(\omega ), \Delta {\hat{P}}_{mn}^{(\Theta )}(\omega ) \}

\rangle&= 0 \nonumber \\ \tan \Theta&= {2 {\tilde{\Delta }}_{mn} \over ({\tilde{\omega }}^{2}-{\tilde{\Delta }}_{mn}^{2}+ {\tilde{g}}_{mn}^{2} +1) +{\text{sgn}}[{\tilde{g}}_{mn}]

\sqrt{({\tilde{\omega }}^{2}-{\tilde{\Delta }}_{mn}^{2}+ {\tilde{g}}_{mn}^{2} +1)^{2} + 4 {\tilde{\Delta }}_{mn}^{2}}}, \end{aligned}$$ (21) where all the parameters are real numbers, and

$$\begin{aligned} \eta&= \frac{\gamma _{i}}{\gamma _{i}+\gamma _{l}} = \frac{T_{i}}{T_{i}+T_{l}} \nonumber \\ {\tilde{\omega }}&= \frac{\omega }{\gamma _{i}+\gamma _{l}} \nonumber \\

{\tilde{g}}_{mn}&= \frac{g}{\gamma _{i}+\gamma _{l}} \mu ^{m+n} \nonumber \\ {\tilde{\Delta }}_{mn}&= \frac{\Delta _{mn}}{\gamma _{i}+\gamma _{l}} = \frac{2\theta _{G}}{T_{i}+T_{l}}

(m+n). \end{aligned}$$ (22) Note that \(\langle \Delta ^{2} {\hat{X}}_{mn}^{(\Theta )}(\omega )\rangle \le 1\) and \(\langle \Delta ^{2} {\hat{P}}_{mn}^{(\Theta )}(\omega )\rangle \ge 1\),

and as \({\tilde{\Delta }}_{mn} \rightarrow 0\), the angle \(\Theta\) is 0 if \(0 \le {\tilde{g}}_{mn}\) or \(\pi /2\) if \({\tilde{g}}_{mn} < 0\). Without loss of generality, we will

focus on the case of \(0 \le {\tilde{g}}_{mn}\) by setting \(0 \le g\) and \(0 \le \mu < 1\) (equivalently, \(0 < \xi \le 1\)). One can further note that the intracavity loss \(T_{l}\)

makes reduction on the cavity escape efficiency \(\eta\). The generated multimode light from the OPO is therefore a collection of individual squeezed vacua in multiple

\({\hbox{HG}}_{{mn}}\) modes, whose modal structure and quantum correlations are described by Eqs. (5) and (21), respectively. In more detail, the spectrum of quantum correlations is

determined by the focusing parameter \(\xi\), modifying \({\tilde{g}}_{mn}\) in Eq. (22), and the waist size is by \(\xi\) and the pump waist \(w_{p}\), as discussed in Eq. (5). For \(\xi =

1\), making \(\mu = 0\), the generated light is a single-mode squeezed vacuum: \({\hbox{HG}}_{{00}}\) contains a squeezed vacuum (\(\langle \Delta ^{2} {\hat{X}}_{00}^{(\Theta )}(\omega

)\rangle < 1\)), but all high-order \({\hbox{HG}}_{{mn}}\) modes (\(m,n\ne 0\)) are vacuum states (\(\langle \Delta ^{2} {\hat{X}}_{mn}^{(\Theta )}(\omega )\rangle = 1\)). On the other

hand, as \(\xi\) becomes smaller than one, \(\mu\) becomes positive, and high-order modes also exhibit squeezing (\(\langle \Delta ^{2} {\hat{X}}_{mn}^{(\Theta )}(\omega )\rangle < 1\)).

Figure 2a compares the squeezing levels \(\langle \Delta ^{2} {\hat{X}}_{mn}^{(\Theta )}(\omega )\rangle\) for different values of \(\xi\). The smaller \(\xi\) exhibits higher squeezing

levels than the larger one for all high orders of \({\hbox{HG}}_{{mn}}\), and the associated Schmidt numbers calculated from Eq. (6) are 8.3 (\(\xi =1/9\)) and 20.7 (\(\xi =1/81\)). The

angles \(\Theta\) for \({\hat{X}}_{mn}^{(\Theta )}(\omega )\) quadratures are all zero as expected. Figure 2b,c show the effects of the Gouy phase shift \(\theta _{G}\) on the generated

light. The Gouy phase creates the detuning \({\tilde{\Delta }}_{mn}\), which affects both the squeezing level and the squeezing angle. For small detunings, the squeezing level and the

squeezing angle remain similar to the ideal self-imaging case, but as \(\theta _{G}\) increases, the squeezing level \(\langle \Delta ^{2} {\hat{X}}_{mn}^{(\Theta )}(\omega )\rangle\)

gradually degrades to zero, and the squeezing angle \(\Theta\) increases to \(\pi /2\). Such effects are stronger for a smaller transmittance \(T_{i}\) and a higher \({\hbox{HG}}_{{mn}}\)

mode, as expected from Eq. (22). In addition, the squeezing level and the squeezing angle depend on the sideband frequency \({\tilde{\omega }}\), as shown in Fig. 2d,e. As

\({\hbox{HG}}_{{00}}\) mode exhibits \({\tilde{\Delta }}_{mn}=0\), it behaves as a common OPO, where the squeezing level decreases while the squeezing angle remains constant as

\({\tilde{\omega }}\) increases. On the other hand, for higher modes where \({\tilde{\Delta }}_{mn} \ne 0\), both of the squeezing level and the squeezing angle depend on the sideband

frequency \({\tilde{\omega }}\). The rotated squeezing angle due to non-zero \({\tilde{\Delta }}_{mn}\) returns to zero as \({\tilde{\omega }}\) increases. The squeezing level, in most

cases, gradually decreases to zero by increasing \({\tilde{\omega }}\), but there is a special case showing a non-monotonic behavior (the blue dashed line for \({\hbox{HG}}_{{02}}\) in Fig. 

2d), which is because a non-zero value of \({\tilde{\omega }}\) makes the minimum value for \(\langle \Delta ^{2} {\hat{X}}_{mn}^{(\Theta )}(\omega )\rangle\): such a case can take place at

\({\tilde{\omega }} = \sqrt{{\tilde{\Delta }}_{mn}^{2} - {\tilde{g}}_{mn}^{2}-1}\) for \({\tilde{\Delta }}_{mn}^{2} > {\tilde{g}}_{mn}^{2}+1\), which can be derived from Eq. (21).

ROBUSTNESS ON SPATIAL MODE MISMATCH Spatial mode mismatch occurs when the mode of quantum light is different from a target mode, e.g. due to beam displacement, tilting, and beam size

difference. Mode mismatch is especially detrimental for couplings with single-mode elements and processes, e.g., optical cavities, optical fibers, frequency conversion, and homodyne

detection. In this section, we will show that the multimode squeezed light from the self-imaging OPO is robust on various types of spatial mode mismatch. When deriving the result, we will

consider mode mismatch only in the _x_-direction, but the same result can be equally obtained for the _y_-direction because of the symmetry of the multimode squeezed light described in Eqs.

(4,5,21). MODE-MISMATCH MODEL To model the spatial mode mismatch, instead of fixing a target mode and varying the modes of quantum light, we will use an equivalent way for the simplicity of

mathematical description: _we fix the quantum light but make deviations on the target mode._ We consider a target mode of \({\hbox{HG}}_{{00}}\) with the waist size of \(w_{t}\)

$$\begin{aligned} \phi _{00} (x,y) = \sqrt{2 \over \pi }{1 \over w_{t}} \exp {\left( -{x^{2} +y^{2} \over w_{t}^{2}}\right) }, \end{aligned}$$ (23) and its deviations due to mode mismatches

[displacement (_d_), tilt (\(\varphi\)), and size difference (_w_)] are $$\begin{aligned} \phi ^{\mathrm{disp}} (x,y;d)&= \sqrt{2 \over \pi }{1 \over w_{t}} \exp {\left( -{(x-d)^{2}

+y^{2} \over w_{t}^{2}}\right) }, \nonumber \\ \phi ^{\mathrm{tilt}} (x,y;\varphi )&= \sqrt{2 \over \pi }{1 \over w_{t}} \exp \left( -{x^{2}+y^{2} \over w_{t}^{2}} + i {2\pi \over

\lambda _0} x \sin \varphi \right) , \nonumber \\ \phi ^{\mathrm{size}} (x,y;w)&= \sqrt{2 \over \pi }{1 \over w} \exp {\left( -{x^{2} +y^{2} \over w^{2}}\right) }, \end{aligned}$$ (24)

respectively. Figure 3a describes the mode mismatches on a target plane. One can expand a mismatched mode \(\phi ^{\mathrm{mis}}\) based on the HG modes \(\phi _{mn}\) stemming from Eq. (23)

$$\begin{aligned} \phi ^{\mathrm{mis}} (x,y;p) = \sum _{mn} \beta _{mn}^{\mathrm{mis}}(p)\, \phi _{mn} (x,y), \end{aligned}$$ (25) where \({\mathrm{mis}} \in \{ {\text{disp,tilt,size}} \}\)

and a mode-mismatching parameter \(p \in \{ d, \varphi , w \}\), and $$\begin{aligned} \beta _{mn}^{\mathrm{disp}} (d)&= {\delta _{n,0} \over \sqrt{m!}} \left( {d \over w_{t}}\right) ^m

\exp \left( -{d^{2} \over 2w_{t}^{2}}\right) , \nonumber \\ \beta _{mn}^{\mathrm{tilt}} (\varphi )&= i^{m+n} {\delta _{n,0} \over \sqrt{m!}} \left( {\pi w_{t} \sin \varphi \over \lambda

_0}\right) ^m \exp \left( -{\pi ^{2} w_{t}^{2} \sin ^{2} \varphi \over 2 \lambda _0^{2}}\right) , \nonumber \\ \beta _{mn}^{\mathrm{size}} (w)&= {\left\{ \begin{array}{ll} 0

&{}\quad n { \text{ or } } m {\text{: } \text{ odd }} \\ {\sqrt{m!n!}\,\left( {1\over 2}\tanh (\ln {w \over w_{t}})\right) ^{m+n \over 2} \over {m \over 2}!{n \over 2}! \cosh ( \ln {w

\over w_{t}})}&{}\quad n { \text{ and } } m {\text{: } \text{ even }} \end{array}\right. }, \end{aligned}$$ (26) and $$\begin{aligned} \phi _{mn} (x,y) ={ \exp \left( {-{{x^{2}+y^{2}}

\over w_{t}^{2}} }\right) H_m\left( {\sqrt{2}x \over w_{t}}\right) H_n\left( {\sqrt{2}y \over w_{t}}\right) \over {w_{t} \sqrt{2^{m+n-1} \pi m!n!} } }. \end{aligned}$$ (27) Figure 4 shows

the coefficients \(\beta _{mn}^{\mathrm{disp}}\), \(\beta _{mn}^{\mathrm{tilt}} (-i)^{m+n}\), and \(\beta _{mn}^{\mathrm{size}}\), which are all real values. As \(d, \varphi , {\text{ and }}

w\) deviate from the ideal mode-matching condition more, \({\hbox{HG}}_{{00}}\) contributes less, which is replaced by the contributions from high-order \({\hbox{HG}}_{{mn}}\) modes. By

defining the creation operator \(({\hat{B}}^{\mathrm{mis}})^\dagger\) for mode \(\phi ^{\mathrm{mis}}\) and \({\hat{B}}^\dagger _{mn}\) for mode \(\phi _{mn}\), Eq. (25) can be expressed as

$$\begin{aligned} ({\hat{B}}^{\mathrm{mis}})^\dagger = \sum _{mn} \beta _{mn}^{\mathrm{mis}}\, {\hat{B}}^\dagger _{mn}. \end{aligned}$$ (28) The effect of mode mismatch can therefore be

understood as contributions from high-order \({\hbox{HG}}_{{mn}}\) modes due to the emergence of non-zero coefficients \(\beta _{mn}^{\mathrm{mis}}\). More specifically, a quadrature

operator for the mismatched mode is written as $$\begin{aligned} {\hat{B}}^{\mathrm{mis}} + \big ({\hat{B}}^{\mathrm{mis}}\big )^{\dagger } = \sum _{mn} {\text{Re}}\left[\beta

_{mn}^{\mathrm{mis}}\right]\big ({\hat{B}}_{mn} + {\hat{B}}^{\dagger }_{mn}\big ) + {\text{Im}}\left[\beta _{mn}^{\mathrm{mis}}\right] \big ({\hat{B}}_{mn} - {\hat{B}}^{\dagger }_{mn}\big

)/i. \end{aligned}$$ (29) When the coefficients are real (\(\beta _{mn} \in {\mathbb{R}}\)) and no correlation exists between different \({\hbox{HG}}_{{mn}}\) and \({\hbox{HG}}_{{kl}}\),

i.e., \(\langle \Delta ({\hat{B}}_{mn} + {\hat{B}}^{\dagger }_{mn}) \Delta ({\hat{B}}_{kl} + {\hat{B}}^{\dagger }_{kl}) \rangle = 0\), the quadrature variance in the mismatched mode is

$$\begin{aligned} \left\langle \Delta ^{2} \left( {\hat{B}}^{\mathrm{mis}} + \big ({\hat{B}}^{\mathrm{mis}}\big )^{\dagger } \right) \right\rangle = \sum _{mn} \, \beta _{mn}^{2} \,

\left\langle \Delta ^{2} \left( {\hat{B}}_{mn} + {\hat{B}}^{\dagger }_{mn} \right) \right\rangle , \end{aligned}$$ (30) which is the weighted mean of the quadrature variances in the

\({\hbox{HG}}_{{mn}}\) modes with the weighting factors of \(\beta _{mn}^{2}\). As the mode mismatch increases, the weight for \({\hbox{HG}}_{{00}}\) decreases, and the noises from

high-order \({\hbox{HG}}_{{mn}}\) come in. Since single-mode squeezed light exhibits a squeezed noise in \({\hbox{HG}}_{{00}}\) and the vacuum noise in \({\hbox{HG}}_{{mn}}\), the squeezing

level quickly degrades to the vacuum noise due to mode mismatch. On the other hand, multimode squeezed light exhibits squeezed noises in high-order \({\hbox{HG}}_{{mn}}\) modes together. As

a result, multimode light can show less degradation on the squeezing level, which, therefore, tolerates more mode mismatch than single-mode light does. MODE-MISMATCH TOLERANCE OF MULTIMODE

SQUEEZED LIGHT We will use the multimode squeezed light in “Quantum properties of multimode squeezed light” section to investigate its robustness on mode mismatch. We first consider the

ideal mode matching of the multimode light with a target mode and then, to account for mode mismatch, we will make deviations on the target mode, as discussed in “Mode-mismatch model”

section. Figure 3b,c depicts linear optical elements through which the multimode light propagate from the OPO to a target plane. The optical elements transform the HG modes \(\psi _{mn}\) in

Eq. (11) into new modes \({\mathscr {I}} [\psi _{mn}]\), which can be obtained by Huygen-Fresnel’s integral \({\mathscr {I}}\) through the associated ABCD matrix31: $$\begin{aligned}

{\mathscr {I}} [\psi _{mn}] ={ 1 \over {w_{1} \sqrt{2^{m+n-1} \pi m!n!} } } \left( {w_{1} \over A w_{c}+2i B/k w_{c}}\right) ^{m+n+1} H_m \left( {\sqrt{2} x \over w_{1}}\right) H_n \left(

{\sqrt{2}y \over w_{1}}\right) \exp \left( {i k{{x^{2}+y^{2}} \over 2 q} }\right) , \end{aligned}$$ (31) where _A_, _B_, _C_,  and _D_ are the matrix elements, and $$\begin{aligned} q&=

{-A (i k w_{c}^{2} /2) + B \over -C (i k w_{c}^{2} /2) + D}, \\ w_{1}^{2}&= A^{2} w_{c}^{2} + (2 B/ k w_{c})^{2}. \end{aligned}$$ First, let us consider the transformation into the image

plane (IP) in Fig. 3b. By choosing focal lengths satisfying \({f_{2} / f_{1}} = {w_{t} / w_{c}}\), the new modes become $$\begin{aligned} {\mathscr {I}}^{\mathrm{IP}} [\psi _{mn}] =

(-1)^{m+n+1} \phi _{mn} (x,y), \end{aligned}$$ (32) which coincides with \(\phi _{mn}\) in Eq. (27) with the additional phase factor \((-1)^{m+n+1}\). Denoting the unitary operation for

\({\mathscr {I}}^{\mathrm{IP}}\) by \({\hat{U}}_{\mathrm{IP}}\), the associated creation operators show a simple relation $$\begin{aligned} {\hat{A}}^\dagger _{mn} =

(-1)^{m+n+1}\,{\hat{U}}_{\mathrm{IP}}^\dagger {\hat{B}}^\dagger _{mn} {\hat{U}}_{\mathrm{IP}}. \end{aligned}$$ (33) Together with Eq. (28), $$\begin{aligned} {\hat{U}}_{\mathrm{IP}}^\dagger

({\hat{B}}^{\mathrm{mis}})^\dagger {\hat{U}}_{\mathrm{IP}} = \sum _{mn} \beta _{mn}^{\mathrm{mis}}\,(-1)^{m+n+1}\, {\hat{A}}^\dagger _{mn}. \end{aligned}$$ (34) We thus obtain the expression

of a quadrature variance at the mismatched mode at sideband frequency \(\omega\): $$\begin{aligned}&\left\langle \Delta ^{2} \left( {\hat{U}}_{\mathrm{IP}}^\dagger

{\hat{X}}^{\mathrm{mis}}(\omega ) {\hat{U}}_{\mathrm{IP}} \right) \right\rangle = {\mathbf{r}} ^ T {\mathbf{V}}(\omega ) {\mathbf{r}}, \end{aligned}$$ (35) where the sideband quadrature

operator \({\hat{X}}^{\mathrm{mis}}(\omega )\) is \({\hat{B}}^{\mathrm{mis}}(\omega ) + ({\hat{B}}^{\mathrm{mis}})^\dagger (-\omega )\), the covariance matrix \({\mathbf{V}}(\omega )\) is

given in Eqs. (20,21), and $$\begin{aligned} {\mathbf{r}}&= [\mathrm{Re}(\gamma _{00}),\ldots ,\mathrm{Im}(\gamma _{00}),\ldots ]^T \nonumber \\ \gamma _{mn}&=\beta

_{mn}^{\mathrm{mis}}\,(-1)^{m+n+1}. \end{aligned}$$ (36) As \({\mathbf{V}}(\omega )\) contains \({\hat{X}}\)-quadrature squeezed vacua in \({\hbox{HG}}_{{mn}}\) modes when \(\theta _{G} =

0\) and \({\tilde{g}}_{mn} > 0\), if \(\gamma _{mn} \in {\mathbb{R}}\), only squeezed-quadrature noises are coupled into the mismatched mode, which makes the multimode squeezed light

robust on mode mismatch. In the image plane, such a condition is satisfied for mode mismatches by displacement and beam-size difference, $$\begin{aligned} \gamma _{mn}^{\mathrm{disp}}&=

\beta _{mn}^{\mathrm{disp}} (-1)^{m+n+1} \in {\mathbb{R}} \nonumber \\ \gamma _{mn}^{\mathrm{size}}&= \beta _{mn}^{\mathrm{size}} (-1)^{m+n+1} \in {\mathbb{R}}. \end{aligned}$$ (37)

Second, we investigate the mode mismatch in the Fourier plane (FP), described in Fig. 3c. The focal length of the lens is chosen as \(f_{1} = w_{t} w_{c} \pi / \lambda _0\). Denoting the

unitary operation for transforming into the Fourier plane by \({\hat{U}}_{\mathrm{FP}}\), the associated creation operators are related as $$\begin{aligned} {\hat{A}}^\dagger _{mn} =

i^{m+n+1}\, {\hat{U}}_{\mathrm{FP}}^\dagger {\hat{B}}^\dagger _{mn} {\hat{U}}_{\mathrm{FP}}, \end{aligned}$$ (38) and thus, the variance by the sideband operator

\({\hat{X}}^{\mathrm{mis}}(\omega ) = {\hat{B}}^{\mathrm{mis}}(\omega ) + ({\hat{B}}^{\mathrm{mis}})^\dagger (-\omega )\) is $$\begin{aligned}&\left\langle \Delta ^{2} \left(

{\hat{U}}_{\mathrm{FP}}^\dagger {\hat{X}}^{\mathrm{mis}}(\omega ) {\hat{U}}_{\mathrm{FP}} \right) \right\rangle = {\mathbf{s}} ^ T {\mathbf{V}}(\omega ) {\mathbf{s}}, \end{aligned}$$ (39)

where $$\begin{aligned} {\mathbf{s}}&= [\mathrm{Re}(\zeta _{00}),\ldots ,\mathrm{Im}(\zeta _{00}),\ldots ]^T \nonumber \\ \zeta _{mn}&=\beta _{mn}^{\mathrm{mis}}\,(-i)^{m+n+1}.

\end{aligned}$$ (40) Like the case of the image plane, the condition \(\zeta _{mn} \in {\mathbb{R}}\) makes the multimode squeezed light robust on mode mismatch. In the Fourier plane,

mismatches by tilt and beam-size difference with an additional \(\pi /2\)-phase shift satisfy the condition, $$\begin{aligned} \zeta _{mn}^{\mathrm{tilt}}&= \beta _{mn}^{\mathrm{tilt}}

(-i)^{m+n+1} e^{i \pi /2} \in {\mathbb{R}} \nonumber \\ \zeta _{mn}^{\mathrm{size}}&= \beta _{mn}^{\mathrm{size}} (-i)^{m+n+1} e^{i \pi /2} \in {\mathbb{R}}. \end{aligned}$$ (41) Figure

5 shows the robustness of the multimode squeezed light \({\mathbf{V}}(\omega )\) on mode mismatch, compared with the result of a single-mode squeezed light in \({\hbox{HG}}_{{00}}\). We

first consider the multimode light by the ideal self-imaging condition (\(\theta _{G}/2\pi =0\), black solid line), and more general cases will be discussed later. As shown in Fig. 5a, when

mode mismatch by displacement (in the image plane) or tilt (in the Fourier plane) occurs, the squeezing level by the single-mode light (original squeezing of 9.5 dB, blue dashed line)

quickly degrades, e.g., less than 3 dB for \(d/w_{t} > 1\) or \(\pi w_{t} \sin \varphi / \lambda _0 > 1\). On the other hand, the multimode light with the same squeezing in

\({\hbox{HG}}_{{00}}\) maintains the squeezing level very well by tolerating the mode mismatch, exhibiting more than 7 dB in the same condition. It is noteworthy that, at sufficiently large

mode mismatch, the multimode light even outperforms single-mode light with infinite squeezing (black dashed line). Furthermore, the multimode squeezed light is robust on beam-size mismatch

on both the image plane and the Fourier plane, as shown in Fig. 5b. Similar to the previous case, the multimode light maintains the squeezing level very well in the influence of mode

mismatch, even outperforming the single-mode infinitely squeezed light. EFFECT OF LOSS Here we investigate the effect of loss on the multimode light in terms of the mode mismatch. In Eqs.

(21,22), the escape efficiency \(\eta\) accounts for the intracavity loss, but it can be generalized to incorporate the total loss in the system, \(1-\eta\), e.g. propagation and detection

losses. Figure 6 shows the squeezing level by mode mismatch for different amounts of losses. \(\eta =1\) corresponds to no loss in the total system (\(1-\eta =0\)), which is identical with

the black solid lines (\(\theta _{G}/2\pi =0\)) in Fig. 5a,b. As the loss increases by reducing \(\eta\), the squeezing level decreases for all the three cases of infinitely squeezed

single-mode light, single-mode squeezed light (9.5 dB), and the multimode light (9.5 dB in \({\hbox{HG}}_{{00}}\) mode). Although such losses exist, we still find that the multimode light is

more robust on mode mismatch than the single-mode light (9.5 dB), and for a sufficiently large mismatch, it again outperforms the infinitely squeezed light. EFFECT OF MODE MISMATCH INSIDE

THE OPO In “Self-imaging OPO”, we assumed that the eigenmodes of the interaction Hamiltonian (4) perfectly match with the cavity modes (11), i.e., the same waist size, \(w_{H} = w_{c}\).

However, mode mismatch can take place inside the OPO due to waist size difference (\(w_{H} \ne w_{c}\)) or the Gaussian approximation (\({\mathrm{sinc}}(x^2) \approx \exp (-\alpha x^{2})\))

used for the Kernel. We investigate how the mode mismatch inside the OPO affects the robustness of multimode light on mode mismatch to a target mode. At first, we consider the waist size

difference (\(w_{H} \ne w_{c}\)) while keeping the Gaussian approximation. To deal with the size difference, we employ a change of basis from the eigenmodes of the interaction Hamiltonian to

the cavity modes $$\begin{aligned} \psi _{mn}(x,y) = \sum _{m',n'} {\mathbf{U}}_{mn,m'n'}(w_{c},w_{H}) \psi ^H_{m',n'}(x,y) \end{aligned}$$ (42) where the

basis change matrix \({\mathbf{U}}(w_{c},w_{H})\) is given as34 $$\begin{aligned} {\mathbf{U}}_{mn,m'n'}(w_{c},w_{H})&= {\left\{ \begin{array}{ll} {\sqrt{m! m'! n!

n'!} \over \cosh ^{m+n+1} \left( \ln {w_{H} \over w_{c}}\right) } \left( {\tanh \left( \ln {w_{H} \over w_{c}}\right) \over 2}\right) ^{m'+n'-m-n\over 2} f\left( \ln {w_{H}

\over w_{c}},m,m'\right) f\left( \ln {w_{H} \over w_{c}},n,n'\right) &{} \vert m-m'\vert \; {\text{and}} \; \vert n-n'\vert {\text{: even}} \\ 0 &{} {\text{else}}

\end{array}\right. } \end{aligned}$$ (43) $$\begin{aligned} f(r,m,m')&= \sum _{ {m-m'\over 2} \le k \le {m\over 2} } \, {(-1)^{k} \left( {\sinh r \over 2}\right) ^{2k} \over

k!(m-2k)!\left( k+{m-m' \over 2}\right) }. \end{aligned}$$ (44) By describing the interaction Hamiltonian in the cavity mode basis, one obtains a modified gain matrix

\(\mathbf{G'}\) $$\begin{aligned} \mathbf{G'} = {\mathbf{U}}(w_{c},w_{H})\,{\mathbf{G}}\,{\mathbf{U}}^{\dagger }(w_{c},w_{H}), \end{aligned}$$ (45) where \({\mathbf{G}}\) is the

original gain matrix in Eq. (18). Differently from \({\mathbf{G}}\), \(\mathbf{G'}\) is a non-diagonal matrix in general. One can use \(\mathbf{G'}\) instead of \({\mathbf{G}}\)

for calculating the covariance matrix (20) and the squeezing levels in target modes (35,39). Figure 7a,b shows that, even with a large difference in waist sizes (\(w_{H} = 1.4 w_{c}\)), the

light from the self-imaging OPO still exhibits robustness on mode mismatch: displacement or tilt in Fig. 7a and beam size in Fig. 7b. This robustness is due to the multimode nature of the

interaction Hamiltonian: although the waist size of the interaction Hamiltonian varies, the interaction Hamiltonian can still provide a multimode gain (\(\mathbf{G'}\)) in the multiple

cavity modes, which in turn generates multimode squeezed light required for robustness on mode mismatch. Second, we consider the interaction Hamiltonian without using the Gaussian

approximation. Let us rewrite the associated kernel (2) using \(w_{p}\), \(\xi\), and \(\alpha\): $$\begin{aligned} {\tilde{K}}({\vec{q}}_{s},{\vec{q}}_{i}) = \exp \left( -{w_{p}^{2}\over 4}

\vert {\vec{q}}_{s}+{\vec{q}}_{i}\vert ^{2}\right) {\mathrm{sinc}} \left( {w_{p}^{2} \over 4} {\xi \over \alpha } \vert {\vec{q}}_{s}-{\vec{q}}_{i}\vert ^{2}\right) . \end{aligned}$$ (46)

We decompose the kernel numerically since analytical expression is unknown due to the inclusion of the sinc function28. The Schmidt number solely depends on \(\xi / \alpha\) because

\(w_{p}\) just acts as the scaling factors of \({\vec{q}}_{s}\) and \({\vec{q}}_{i}\). To compare the properties of the original Hamiltonian (2,46) and those by the approximated one (4), we

find, for a given \(\xi\), the coefficient \(\alpha\) that gives the same Schmidt number as the Gaussian approximation (6); this way of choosing \(\alpha\) is justified because the

robustness on mode mismatch originates from the occupation of squeezed light in multiple modes, depending highly on the Schmidt number. For \(\xi =1/81\), the corresponding \(\alpha\) is

0.46. In addition, \(w_{p}\) is determined by maximizing the overlap between the first eigenmode of Eq. (46) and the \({\hbox{HG}}_{{00}}\) cavity mode. A modified gain matrix

\(\mathbf{G'}\) is then obtained by $$\begin{aligned} \mathbf{G'}_{mn,m'n'} = g\int d^{2}{\vec{x}}_{s} d^{2}{\vec{x}}_{i} \, K'({\vec{x}}_{s},{\vec{x}}_{i})\psi

_{mn}({\vec{x}}_{s})\psi _{m'n'}({\vec{x}}_{i}), \end{aligned}$$ (47) where \(K'({\vec{x}}_{s},{\vec{x}}_{i})\) is the inverse Fourier transform of Eq. (46), and \(\psi

_{mn}(x,y)\) are the cavity modes defined in Eq. (11). \(\mathbf{G'}\), being a non-diagonal matrix, is used instead of \({\mathbf{G}}\) to find the covariance matrix (20) and the

squeezing levels in target modes (35,39). In Fig. 7c,d, we compare the robustness of mode mismatch by the original Hamiltonian and by the approximated Hamiltonian. It is evident that both

cases exhibit robustness on mode mismatch by outperforming the single-mode squeezed light. In Fig. 7c with \(\theta _{G}/2\pi = 0\), one can find that the original Hamiltonian shows a

slightly better performance than the approximated one. It is because, while the Schmidt numbers are the same, the eigenvalue spectrum of the original Hamiltonian is distributed more toward

lower-order eigenmodes than that of the approximated Hamiltonian, which is advantageous for a small amount of mode mismatch. At \(\theta _{G}/2\pi = 0.002\), their difference becomes

negligible because of the squeezing angle rotation in high-order modes. In Fig. 7d with \(\theta _{G}/2\pi = 0\), the original Hamiltonian shows better squeezing level for \(w/w_{t} > 1\)

but worse for \(w/w_{t} < 1\) when compared with the approximated Hamiltonian: the asymmetry comes from the negative correlations between even-order \({\hbox{HG}}_{{mn}}\) modes for the

original Hamiltonian (e.g., \(\mathbf{G'}_{00,04}\), \(\mathbf{G'}_{00,22} < 0\) in Eq. (47)). At \(\theta _{G}/2\pi = 0.001\), the difference in the performances of the two

Hamiltonians is negligible as in the case of Fig. 7c. EFFECT OF GOUY PHASE SHIFT Until now, we have explored the robustness on mode mismatch in the ideal self-imaging condition. For stable

operation of the OPO, however, a small detuning by the Gouy phase shift is necessary22. The detuning degrades the squeezing level and rotates the squeezing angle for high-order HG modes, as

discussed in Fig. 2. Here we investigate whether the robustness on mode mismatch can still be sustained with detunings from the ideal condition. Figure 5 compares the squeezing levels

coupled in a target mode with non-zero Gouy phase shifts, \(\theta _{G} / 2\pi = 0.002, 0.004\), and 0.006 for the displace/tilt mismatching and \(\theta _{G} / 2\pi = 0.001, 0.002\), and

0.003 for the size mismatching. As expected, the squeezing level becomes degraded as more Gouy phase shift is introduced. For \(\theta _{G} / 2\pi = 0.002\) in (a) and \(\theta _{G} / 2\pi =

0.001\) in (b), the generated multimode light can still beat the performance of the infinitely squeezed single-mode light for a sufficiently large mismatch. The cases of \(\theta _{G} /

2\pi = 0.004\) in (a) and \(\theta _{G} / 2\pi = 0.002\) in (b) exhibit a squeezing level worse than the infinitely squeezed light but better than 9.5 dB squeezed single-mode light. However,

we find no advantage in using the multimode light with \(\theta _{G} / 2\pi = 0.006\) in (a) and \(\theta _{G} / 2\pi = 0.003\) in (b), being worse than the 9.5 dB single-mode light; in

this regime, due to the rotations of the squeezing angles of high-order HG modes in Fig. 2c, \({\hat{X}}_{mn}(\omega )\) quadratures exhibit larger noises than the vacuum noise. To take

advantage of using multimode light, keeping a small-enough Gouy phase shift is required. We, therefore, investigate how small Gouy phase shift is required to exhibit advantages of using

multimode squeezed light. For the quantification, we define an enhancement factor \({\mathscr {F}}\) in decibels, $$\begin{aligned} {\mathscr {F}} = -10 \log _{10} \left[ { \Delta ^{2}

{\hat{X}}^{({\mathrm{mul}})} \over \Delta ^{2} {\hat{X}}^{({\mathrm{sin}})} } \right] , \end{aligned}$$ (48) where \(\Delta ^{2} {\hat{X}}^{({\mathrm{sin}})}\) is the squeezing level by

single-mode squeezed light, and \(\Delta ^{2} {\hat{X}}^{({\mathrm{mul}})}\) is the squeezing level by multimode squeezed light (having the same initial squeezing level in

\({\hbox{HG}}_{{00}}\) as the single-mode light). A positive value of \({\mathscr {F}}\) indicates that the multimode squeezed light is more robust to mode mismatch than the single-mode

squeezed light. As the Gouy phase shift is determined by the detuning ratios \(\Delta l_{1} /R\) and \(\Delta l_{2} /R\), as given in Eq. (10), we calculate the enhancement factor as varying

the detunings. Figure 8 shows the enhancement factor of using the multimode squeezed light when the mode overlap by mismatch is 50% (corresponding to the dashed lines at \(d/w_{t} = \pi

w_{t} \sin \varphi /\lambda _0 =0.83\) and \(w/w_{t}=2.45\) in Fig. 4). A broad range of \(\Delta l_{1} /R\) and \(\Delta l_{2} /R\) exhibits enhancements compared with the single-mode case.

Comparing (a) and (b) in Fig. 8, mode mismatch by size difference requires more stringent conditions for the enhancement; this is because size difference involves higher-orders of HG modes

than those by displacement and tilt, as shown in Fig. 4, and the squeezed lights in higher-order modes are more susceptible to the Gouy phase shift as shown in Fig. 2b,c. However, these

stringent conditions are still achievable using only off-the-shelf positioning devices: a typical OPO employs a curved mirror with the radius of the curvature in the order of \(R=100\) mm,

and position controllability in the order of 100 \(\upmu\)m (e.g. by using a linear stage) can readily achieve very small values of \(\Delta l_{1} /R, \Delta l_{2} /R = 0.001\). CONCLUSION

In this paper, we have shown that multimode squeezed light generated from a self-imaging OPO is robust on spatial mode mismatch. First, we found an analytic form of the quantum properties of

the multimode light at sidebands frequency by taking into account the Gouy phase shift (required for OPO stability) and the intracavity loss. By decomposing mode mismatches of displacement,

tilt, and size difference into a \({\hbox{HG}}_{{mn}}\) mode basis, we found that the mode mismatches induce contributions from high-order \({\hbox{HG}}_{{mn}}\) modes, which makes the

multimode squeezed light robust on mode mismatch. We showed that the multimode light from the self-imaging OPO with a small Gouy phase shift can even outperform the single-mode infinitely

squeezed light, in terms of displacement and size difference in the image plane and of tilt and size difference in the Fourier plane. Such robustness on the multiple cases of mode mismatch

is made possible because of the fully degenerate nature of the self-imaging OPO, which cannot be accomplished by using a confocal OPO18 or two single-mode OPOs16. Our work of mitigating the

mode mismatching loss will have broad applications to quantum technologies based on squeezed light, e.g., quantum-enhanced gravitational-wave detection11,12, deterministic quantum

teleportation7, measurement-based quantum computing1,2,3,4, and Gaussian boson sampling5,6. REFERENCES * Asavanant, W. _et al._ Generation of time-domain-multiplexed two-dimensional cluster

state. _Science (New York, NY)_ 366, 373–376 (2019). Article  ADS  MathSciNet  CAS  Google Scholar  * Larsen, M. V., Guo, X., Breum, C. R., Neergaard-Nielsen, J. S. & Andersen, U. L.

Deterministic generation of a two-dimensional cluster state. _Science (New York, NY)_ 366, 369–372 (2019). Article  ADS  MathSciNet  CAS  Google Scholar  * Ra, Y.-S. _et al._ Non-Gaussian

quantum states of a multimode light field. _Nat. Phys._ 16, 144–147 (2020). Article  CAS  Google Scholar  * Pfister, O. Continuous-variable quantum computing in the quantum optical frequency

comb. _J. Phys. B At. Mol. Opt. Phys._ 53, 012001 (2020). Article  ADS  CAS  Google Scholar  * Zhong, H.-S. _et al._ Quantum computational advantage using photons. _Science (New York, NY)_

370, 1460–1463 (2020). Article  ADS  CAS  Google Scholar  * Arrazola, J. M. _et al._ Quantum circuits with many photons on a programmable nanophotonic chip. _Nature_ 591, 54–60 (2021).

Article  ADS  CAS  Google Scholar  * Liu, S., Lou, Y. & Jing, J. Orbital angular momentum multiplexed deterministic all-optical quantum teleportation. _Nat. Commun._ 11, 3875 (2020).

Article  ADS  CAS  Google Scholar  * Giovannetti, V., Lloyd, S. & Maccone, L. Quantum-enhanced measurements: Beating the standard quantum limit. _Science_ 306, 1330–1336 (2004). Article

  ADS  CAS  Google Scholar  * Taylor, M. A. _et al._ Biological measurement beyond the quantum limit. _Nat. Photonics_ 7, 229–233 (2013). Article  ADS  CAS  Google Scholar  * Guo, X. _et

al._ Distributed quantum sensing in a continuous-variable entangled network. _Nat. Phys._ 16, 281–284 (2020). Article  CAS  Google Scholar  * Tse, M. _et al._ Quantum-enhanced advanced LIGO

detectors in the era of gravitational-wave astronomy. _Phys. Rev. Lett._ 123, 231107 (2019). Article  ADS  CAS  Google Scholar  * Acernese, F. _et al._ Increasing the astrophysical reach of

the advanced virgo detector via the application of squeezed vacuum states of light. _Phys. Rev. Lett._ 123, 231108 (2019). Article  ADS  CAS  Google Scholar  * Vahlbruch, H., Mehmet, M.,

Danzmann, K. & Schnabel, R. Detection of 15 dB squeezed states of light and their application for the absolute calibration of photoelectric quantum efficiency. _Phys. Rev. Lett._ 117,

110801 (2016). Article  ADS  Google Scholar  * Oelker, E., Barsotti, L., Dwyer, S., Sigg, D. & Mavalvala, N. Squeezed light for advanced gravitational wave detectors and beyond. _Opt.

Express_ 22, 21106–21121 (2014). Article  ADS  CAS  Google Scholar  * Töyrä, D. _et al._ Multi-spatial-mode effects in squeezed-light-enhanced interferometric gravitational wave detectors.

_Phys. Rev. D_ 96, 022006 (2017). Article  ADS  Google Scholar  * Steinlechner, S. _et al._ Mitigating mode-matching loss in nonclassical laser interferometry. _Phys. Rev. Lett._ 121, 263602

(2018). Article  ADS  CAS  Google Scholar  * Wittel, H. Active and passive reduction of high order modes in the gravitational wave detector GEO 600. PhD Thesis (2015). * Lugiato, L. A.

& Grangier, P. Improving quantum-noise reduction with spatially multimode squeezed light. _J. Opt. Soc. Am. B_ 14, 225–231 (1997). Article  ADS  CAS  Google Scholar  * Embrey, C. S.,

Turnbull, M. T., Petrov, P. G. & Boyer, V. Observation of localized multi-spatial-mode quadrature squeezing. _Phys. Rev. X_ 5, 1097 (2015). Google Scholar  * Hsu, M. T. L., Delaubert,

V., Lam, P. K. & Bowen, W. P. Optimal optical measurement of small displacements. _J. Opt. B Quantum Semiclass. Opt._ 6, 495–501 (2004). Article  ADS  Google Scholar  * Arnaud, J. A.

Degenerate optical cavities. _Appl. Opt._ 8, 189–196 (1969). Article  ADS  CAS  Google Scholar  * Chalopin, B., Chiummo, A., Fabre, C., Maître, A. & Treps, N. Frequency doubling of low

power images using a self-imaging cavity. _Opt. Express_ 18, 8033–8042 (2010). Article  ADS  CAS  Google Scholar  * Lopez, L. _et al._ Multimode quantum properties of a self-imaging optical

parametric oscillator: Squeezed vacuum and Einstein–Podolsky–Rosen-beams generation. _Phys. Rev. A_ 80, 043816 (2009). Article  ADS  Google Scholar  * Chalopin, B., Scazza, F., Fabre, C.

& Treps, N. Multimode nonclassical light generation through the optical-parametric-oscillator threshold. _Phys. Rev. A_ 81, 061804 (2010). Article  ADS  Google Scholar  * Chalopin, B.,

Scazza, F., Fabre, C. & Treps, N. Direct generation of a multi-transverse mode non-classical state of light. _Opt. Express_ 19, 4405–4410 (2011). Article  ADS  Google Scholar  * Caspani,

L., Brambilla, E. & Gatti, A. Tailoring the spatiotemporal structure of biphoton entanglement in type-I parametric down-conversion. _Phys. Rev. A_ 81, 033808 (2010). Article  ADS 

Google Scholar  * Monken, C. H., Ribeiro, P. H. S. & Pádua, S. Transfer of angular spectrum and image formation in spontaneous parametric down-conversion. _Phys. Rev. A_ 57, 3123–3126

(1998). Article  ADS  CAS  Google Scholar  * Straupe, S. S., Ivanov, D. P., Kalinkin, A. A., Bobrov, I. B. & Kulik, S. P. Angular Schmidt modes in spontaneous parametric down-conversion.

_Phys. Rev. A_ 83, 060302 (2011). Article  ADS  Google Scholar  * Miatto, F. M., Brougham, T. & Yao, A. M. Spatial Schmidt modes generated in parametric down-conversion. _Eur. Phys. J.

D_ 66, 183 (2012). Article  ADS  Google Scholar  * Law, C. K. & Eberly, J. H. Analysis and interpretation of high transverse entanglement in optical parametric down conversion. _Phys.

Rev. Lett._ 92, 127903 (2004). Article  ADS  CAS  Google Scholar  * Siegman, A. E. _Lasers_ (University Science Books, Sausalito, 1986). Google Scholar  * Gigan, S., Lopez, L., Treps, N.,

Maître, A. & Fabre, C. Image transmission through a stable paraxial cavity. _Phys. Rev. A_ 72, 023804 (2005). Article  ADS  Google Scholar  * Gardiner, C. W. & Collett, M. J. Input

and output in damped quantum systems: Quantum stochastic differential equations and the master equation. _Phys. Rev. A_ 31, 3761–3774 (1985). Article  ADS  MathSciNet  CAS  Google Scholar  *

Kim, M. S., De Oliveira, F. A. M. & Knight, P. L. Properties of squeezed number states and squeezed thermal states. _Phys. Rev. A_ 40, 2494 (1989). Article  ADS  CAS  Google Scholar 

Download references ACKNOWLEDGEMENTS This work was supported by the Korea Astronomy and Space Science Institute under the R&D program (Project No. 2021-1-810-04), the Ministry of Science

and ICT (NRF-2019R1C1C1005196), and MSIT of Korea under the ITRC support program (IITP-2021-2020-0-01606). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Physics, Korea

Advanced Institute of Science and Technology, Daejeon, 34141, Korea Chan Roh, Geunhee Gwak & Young-Sik Ra Authors * Chan Roh View author publications You can also search for this author

inPubMed Google Scholar * Geunhee Gwak View author publications You can also search for this author inPubMed Google Scholar * Young-Sik Ra View author publications You can also search for

this author inPubMed Google Scholar CONTRIBUTIONS C.R. and Y.-S.R. developed the theoretical model. C.R. and G.G. performed numerical analysis and simulations. Y.-S.R. supervised the

project. All authors discussed the results and contributed to writing the manuscript. CORRESPONDING AUTHOR Correspondence to Young-Sik Ra. ETHICS DECLARATIONS COMPETING INTERESTS The authors

declare no competing interests. ADDITIONAL INFORMATION PUBLISHER'S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional

affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution

and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if

changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the

material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will

need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE

CITE THIS ARTICLE Roh, C., Gwak, G. & Ra, YS. Robust squeezed light against mode mismatch using a self imaging optical parametric oscillator. _Sci Rep_ 11, 18991 (2021).

https://doi.org/10.1038/s41598-021-98328-7 Download citation * Received: 06 July 2021 * Accepted: 07 September 2021 * Published: 23 September 2021 * DOI:

https://doi.org/10.1038/s41598-021-98328-7 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative