The type-reproduction number of sexually transmitted infections through heterosexual and vertical transmission

ABSTRACT Multiple sexually transmitted infections (STIs) have threatened human health for centuries. Most STIs spread not only through sexual (horizontal) transmission but also through

mother-to-child (vertical) transmission. In a previous work (Ito _et al_. 2019), we studied a simple model including heterosexual and mother-to-child transmission and proposed a formulation

of the basic reproduction number over generations. In the present study, we improved the model to take into account some factors neglected in the previous work: adult mortality from

infection, infant mortality caused by mother-to-child transmission, infertility or stillbirth caused by infection, and recovery with treatment. We showed that the addition of these factors

has no essential effect on the theoretical formulation. To study the characteristics of the epidemic threshold, we derived analytical formulas for three type-reproduction numbers for adult

men, adult women and juveniles. Our result indicates that if an efficient vaccine exists for a prevalent STI, vaccination of females is more effective for containment of the STI than

vaccination of males, because the type-reproduction number for adult men is larger than that for adult women when they are larger than one. SIMILAR CONTENT BEING VIEWED BY OTHERS MODELLING

THE MULTIPLE ANATOMICAL SITE TRANSMISSION OF _MYCOPLASMA GENITALIUM_ AMONG MEN WHO HAVE SEX WITH MEN IN AUSTRALIA Article Open access 27 May 2021 A NEW EPIDEMIC MODEL OF SEXUALLY

TRANSMITTABLE DISEASES: A FRACTIONAL NUMERICAL APPROACH Article Open access 30 January 2025 ON MATERNITY AND THE STRONGER IMMUNE RESPONSE IN WOMEN Article Open access 18 August 2022

INTRODUCTION Although sex is a private and pleasurable activity, it may result in disease1. Largely because of human instinct, sexually transmitted infections (STIs) have continued to exist

alongside human beings for a long time. In fact, STIs were described in ancient records such as the Ebers Papyrus and the Old Testament of the Bible in Leviticus 15: 2–332. STIs remain a

worldwide health concern, with a global estimate of 340 million new cases of “curable” infections (e.g., syphilis, gonorrhea, chlamydia, and trichomoniasis) and millions of “incurable”

infections (e.g., human immunodeficiency virus [HIV], herpes simplex viruses [HSV], human papillomaviruses [HPV], hepatitis B virus [HBV], and human T-lymphotropic virus type 1 [HTLV-1])

occurring annually among men and women aged 15–49 years3,4. The “incurable” viral STIs cannot be eradicated through medications that are currently available. Presently, some STIs that were

formerly considered “curable” are spreading as STIs that are “incurable” because of resistance to antibiotics5,6. It is difficult to accurately estimate mortality due to STIs because death

certificates generally only record prevalent conditions, and STIs are rarely recorded on death certificates7. However, STIs contribute both directly and indirectly to human death. HIV has

been well known as the virus that causes AIDS, which has a high mortality rate. In 2017, although the number of new infected people with HIV has begun to decline gradually, 36.9 million

people were living with HIV/AIDS, and 940,000 people died of HIV-related illnesses, worldwide8,9. Hepatitis B and hepatitis C are also dangerous STIs, which increase the mortality rates from

cirrhosis and liver cancer10. From 1990 to 2013, the estimated number of deaths caused by hepatitis, globally, increased from around 0.9 million to around 1.5 million10. HPV causes

virtually all cervical cancer and associated cancers (i.e., oropharyngeal, vulvar, vaginal, penile, and anal cancers)11. Cervical cancer is among the most common cancers causing death for

women in developing countries12. In 2018, there were 570,000 new cases of cervical cancer, worldwide, and 311,000 women died from cervical cancer13. Reviewing the current situation, Chesson

_et al_. estimated the direct costs of major STIs at US$16.7 billion, including costs for gonorrhea, chlamydia, syphilis, trichomoniasis, hepatitis B, diseases associated with sexually

transmitted HPV, genital HSV-2 infection, and HIV infection14,15. In light of these concerns, mathematical models can provide ideas and knowledge that are helpful for understanding the

epidemiology and control of STIs16. Many mathematical models have been built to understand the infection dynamics of STIs, including HIV/AIDS, syphilis, and gonorrhea16,17. The first

mathematical model used for the explicit study of an STI (gonorrhea) was developed by Cooke and Yorke in 197318. The mathematical model of HIV transmission has been extensively studied since

the late 1980s19,20,21. Simple models have the advantage of analytical tractability and can be used to explain the relative merits of various prevention options. However, the real world is

replete with complexities22. STIs occur through sexual contact networks, which are extremely complex. The overall picture of sexual networks is unclear because information about who has sex

with whom is considered extremely sensitive. We do know that human sexual networks are highly heterogeneous: Most individuals have only a few sexual partners, but a few have

hundreds23,24,25,26. Therefore, the heterogeneity of sexual contact is an important factor of the spread of STIs. Most STIs can also be spread vertically over generations through

mother-to-child transmission. There are various types of STIs, and their transmission processes are diverse. For example, the primary route of mother-to-child (vertical) transmission of

HTLV-1 is breastfeeding; intrauterine transmission and transmission via saliva are also possible infection routes, but their transmission rates are low27. For HTLV-1 and HBV, children who

are infected through mother-to-child transmission spread STIs through sexual contact after they become adults because HTLV-1 and HBV have long latency periods before the onset of symptoms

and extremely low or zero mortality among infants infected through mother-to-child transmission28,29. In contrast, many other STIs (e.g., congenital syphilis, neonatal herpes, congenital

HIV, and many other bacterial STIs) have high infant mortality rates or other serious consequences for infants30,31,32,33,34. Clearly, these high-mortality STIs will lead to different

infection dynamics, compared with low-mortality STIs. Understanding the long-term dynamics of various STIs requires a comprehensive model that includes both horizontal and vertical

transmission. In a previous study, we tested a susceptible–infected model with horizontal and vertical transmission35. However, the previous model assumed that the pathogenic death rate

coincided with the non-pathogenic death rate, that an individual could have sexual contact soon after birth, and that infections were incurable. In the present study, we improved the

previous model and constructed a comprehensive model that takes into account adult mortality from infection, infant mortality caused by mother-to-child transmission, infertility or

stillbirth caused by infection, and recovery with treatment. Thus, the comprehensive model can be considered a susceptible–infected–susceptible (SIS) model. This model includes three types

of individuals: juveniles, adult women, and adult men. Here, juveniles are individuals who are not mature enough to have sexual intercourse. In addition, to reproduce heterogeneous sexual

contacts, we assume that each individual has their own sexual activity. In the previous study, we considered the dynamics of sexual networks35; however, for simplicity, we assume sexual

contacts to be well mixed in the present study. When considering homogeneous populations, epidemiologists frequently use the basic reproduction number (_R_0), which is the number of

secondary cases that one case would produce in a completely susceptible population. However, because our model includes three types of individuals, it was convenient to calculate a

type-reproduction number for each type category rather than for the population as a whole36,37. If the type-reproduction numbers are larger than one, the basic reproduction number is also

larger than one. The type-reproduction numbers have a significant meaning from a long-term public health perspective: STIs can spread when the type-reproduction numbers are larger than one,

and STIs cannot survive in the long term when the type-reproduction numbers are less than one. In this article, we derive analytical formulas for the three type-reproduction numbers using

the comprehensive model we propose. We show that the type-reproduction number for adult women is qualitatively the same as the basic reproduction number proposed in our previous work35.

MODEL We consider a compartment model with six compartments: susceptible juveniles _S_j(_t_), susceptible adult female _S_f(_t_), susceptible adult male _S_m(_t_), infected juveniles

_I_j(_t_), infected adult female _I_f(_t_), and infected adult male _I_m(_t_). These variables represent the numbers of individuals belonging to the compartments at time _t_. Juveniles

cannot have sexual intercourse, whereas adults can. Moreover, we assume that each adult has different sexual activity, as a congenital attribute. The model variables and parameters are

summarized in Table 1. DYNAMICS OF JUVENILES The dynamics of _S_j(_t_) and _I_j(_t_) are assumed to be $$\begin{array}{ccc}\frac{d{S}_{{\rm{j}}}(t)}{dt} & = &

B\frac{{S}_{{\rm{f}}}(t)+(1-\alpha )(1-\delta ){I}_{{\rm{f}}}(t)}{{I}_{{\rm{f}}}(t)+{S}_{{\rm{f}}}(t)}-(\lambda +{\mu }_{{\rm{j}}}){S}_{{\rm{j}}}({\rm{t}})+{\eta

}_{{\rm{j}}}{I}_{{\rm{j}}}(t),\\ \frac{d{I}_{{\rm{j}}}(t)}{dt} & = & B\frac{\alpha (1-\delta ){I}_{{\rm{f}}}(t)}{{I}_{{\rm{f}}}(t)+{S}_{{\rm{f}}}(t)}-(\lambda ^{\prime} +{\eta

}_{{\rm{j}}}+{\mu }_{{\rm{j}}}^{\text{'}}){I}_{{\rm{j}}}(t).\end{array}$$ (1) Here, _B_ is the number of births per unit of time, _δ_ is the rate of infertility or stillbirth, and _α_

is the rate of vertical transmission from mother to infant. The parameters _λ_ and _λ_′ are the maturing rates for susceptible and infected juveniles, respectively. Juveniles become adults

at the maturing rate. Because the pathogenicity of infection may reduce the growth of infected juveniles, we set _λ_′ ≤ _λ_. The parameter _η_j stands for the juvenile cure rate, where an

infected juvenile becomes susceptible with the cure rate of _η_j. The pathogenic premature mortality rate \({\mu }_{{\rm{j}}}^{\text{'}}\) is at least as large as the natural premature

mortality rate _μ_j (thus, \({\mu }_{{\rm{j}}}^{\text{'}}\ge {\mu }_{{\rm{j}}}\)). Here, the juvenile’s sex is not considered because there is no need to distinguish between sexes in

the juvenile stage in this model. SEXUAL ACTIVITY We assume that each adult individual has sexual activity _a_ as part of their constitution. Anderson and May defined the degree of sexual

activity as the number of sexual partners per unit of time17,21. In contrast, in network science, the degree of sexual activity is often defined as the number sexual partners that an

individual has at the same time38. Here, we generalize degree of sexual activity to be a real number and define it as follows39,40. We assume that the sexual activity levels of women and men

follow the distributions _p_f(_a_) and _p_m(_a_), respectively. We set the mean sexual activity levels _a_ of women and men to one without losing generality: $$\langle a\rangle ={\int

}_{0}^{\infty }\,a{p}_{{\rm{f}}}(a)da={\int }_{0}^{\infty }\,a{p}_{{\rm{m}}}(a)da=1.$$ (2) The total number of sexual contacts per unit of time is assumed to be _f_(_N_f(_t_), _N_m(_t_)),

where _N_f(_t_) = _S_f(_t_) + _I_f(_t_) and _N_m(_t_) = _S_m(_t_) + _I_m(_t_). Thus, the rates of having a sexual contact for a woman and a man are

$$af({N}_{{\rm{f}}}(t),{N}_{{\rm{m}}}(t))/{N}_{{\rm{f}}}(t),\,af({N}_{{\rm{f}}}(t),{N}_{{\rm{m}}}(t))/{N}_{{\rm{m}}}(t),$$ (3) respectively. For example, if sexual contacts are modeled by

mass action, _f_(_N_f(_t_), _N_m(_t_)) ∝ _N_f(_t_)_N_m(_t_). In this case, the rates of having a sexual contact for a woman and a man are proportional to _aN_m(_t_) and _aN_f(t),

respectively. This is not very realistic because the number of sexual contacts a person has increases along with the population. Alternatively, if women dominate sexual contact,

_f_(_N_f(_t_), _N_m(_t_)) ∝ _N_f(_t_). In this case, the rates of having a sexual contact for a woman and a man are proportional to _a_ and _aN_f(t)/_N_m(_t_), respectively. This may be more

suitable because men have less chance of contacting women when the number of women per men decreases. In any case, the sexual contacts are assumed to be well mixed. The average numbers of

sexual contacts per unit of time for women and men are given as

$${k}_{{\rm{f}}}=\frac{f({N}_{{\rm{f}}}(t),{N}_{{\rm{m}}}(t))}{{N}_{{\rm{f}}}(t)},\,{k}_{{\rm{m}}}=\frac{f({N}_{{\rm{f}}}(t),{N}_{{\rm{m}}}(t))}{{N}_{{\rm{m}}}(t)},$$ (4) respectively,

because we set 〈_a_〉 = 1. Moreover, it is convenient to define the averages weighted by sexual activity: $$\begin{array}{ccc}{c}_{{\rm{f}}} & = &

\frac{f({N}_{{\rm{f}}}(t),{N}_{{\rm{m}}}(t))}{{N}_{{\rm{f}}}(t)}{\int }_{0}^{\infty }\,{a}^{2}{p}_{{\rm{f}}}(a)da,\\ {c}_{{\rm{m}}} & = &

\frac{f({N}_{{\rm{f}}}(t),{N}_{{\rm{m}}}(t))}{{N}_{{\rm{m}}}(t)}{\int }_{0}^{\infty }\,{a}^{2}{p}_{{\rm{m}}}(a)da.\end{array}$$ (5) These values correspond to the effective average over the

distribution by degree of sexual activity, as defined by May and Anderson21, where _c_f and _c_m are not simply the mean but the mean plus the ratio of variance to the mean. High

heterogeneity of sexual contacts means _c_f ≫ _k_f and _c_m ≫ _k_m. DYNAMICS OF ADULTS The number of susceptible adult women whose sexual activity is in the infinitesimal interval [_a_, _a_ 

+ _da_] is denoted as _S_f(_t_, _a_)_da_. The same applies to _S_m(_t_, _a_), _I_f(_t_, _a_) and _I_m(_t_, _a_). Thus, we have $$\begin{array}{ccc}{S}_{{\rm{f}}}(t) & = & {\int

}_{0}^{\infty }\,{S}_{{\rm{f}}}(t,a)da,\,{S}_{{\rm{m}}}(t)={\int }_{0}^{\infty }\,{S}_{{\rm{m}}}(t,a)da,\,\\ {I}_{{\rm{f}}}(t) & = & {\int }_{0}^{\infty

}\,{I}_{{\rm{f}}}(t,a)da,\,{I}_{{\rm{m}}}(t)={\int }_{0}^{\infty }\,{I}_{{\rm{m}}}(t,a)da.\end{array}$$ (6) The dynamics of _S_f(_t_, _a_), _I_f(_t_, _a_), _S_m(_t_, _a_) and _I_m(_t_, _a_)

are expressed as $$\begin{array}{ccc}\frac{{\rm{\partial }}{S}_{{\rm{f}}}(t,a)}{{\rm{\partial }}t} & = & \lambda (1-\gamma ){S}_{{\rm{j}}}(t){p}_{{\rm{f}}}(a)-{\mu

}_{{\rm{f}}}{S}_{{\rm{f}}}(t,a)+{\eta }_{{\rm{f}}}{I}_{{\rm{f}}}(t,a)\\ & & -\,a{\beta }_{{\rm{m}}\to {\rm{f}}}{S}_{{\rm{f}}}(t,a){{\rm{\Theta

}}}_{{\rm{m}}}(t)\frac{f({N}_{{\rm{f}}}(t),{N}_{{\rm{m}}}(t))}{{N}_{{\rm{f}}}(t)},\\ \frac{{\rm{\partial }}{S}_{{\rm{m}}}(t,a)}{{\rm{\partial }}t} & = & \lambda \gamma

{S}_{{\rm{j}}}(t){p}_{{\rm{m}}}(a)-{\mu }_{{\rm{m}}}{S}_{{\rm{m}}}(t,a)+{\eta }_{{\rm{m}}}{I}_{{\rm{m}}}(t,a)\\ & & -\,a{\beta }_{{\rm{f}}\to {\rm{m}}}{S}_{{\rm{m}}}(t,a){{\rm{\Theta

}}}_{{\rm{f}}}(t)\frac{f({N}_{{\rm{f}}}(t),{N}_{{\rm{m}}}(t))}{{N}_{{\rm{m}}}(t)},\\ \frac{{\rm{\partial }}{I}_{{\rm{f}}}(t,a)}{{\rm{\partial }}t} & = & {\lambda }^{^{\prime}

}(1-\gamma ){I}_{{\rm{j}}}(t){p}_{{\rm{f}}}(a)-({\mu }_{{\rm{f}}}^{^{\prime} }+{\eta }_{{\rm{f}}}){I}_{{\rm{f}}}(t,a)\\ & & +\,a{\beta }_{{\rm{m}}\to

{\rm{f}}}{S}_{{\rm{f}}}(t,a){{\rm{\Theta }}}_{{\rm{m}}}(t)\frac{f({N}_{{\rm{f}}}(t),{N}_{{\rm{m}}}(t))}{{N}_{{\rm{f}}}(t)},\\ \frac{{\rm{\partial }}{I}_{{\rm{m}}}(t,a)}{{\rm{\partial }}t}

& = & {\lambda }^{^{\prime} }\gamma {I}_{{\rm{j}}}(t){p}_{{\rm{m}}}(a)-({\mu }_{{\rm{m}}}^{^{\prime} }+{\eta }_{{\rm{m}}}){I}_{{\rm{m}}}(t,a)\\ & & +\,a{\beta }_{{\rm{f}}\to

{\rm{m}}}{S}_{{\rm{m}}}(t,a){{\rm{\Theta }}}_{{\rm{f}}}(t)\frac{f({N}_{{\rm{f}}}(t),{N}_{{\rm{m}}}(t))}{{N}_{{\rm{m}}}(t)}.\end{array}$$ (7) The parameter _γ_ in the first terms on the right

hand side of the above equations represents the proportion of men at the time of coming of age. If _γ_ = 0.5, the same number of male and female juveniles grow to adulthood. The parameters

_μ_f, \({\mu }_{{\rm{f}}}^{\text{'}}\), _μ_m, and \({\mu }_{{\rm{m}}}^{\text{'}}\) are the death rates for susceptible adult women, infected adult women, susceptible adult men, and

infected adult men, respectively. Here, we set \({\mu }_{{\rm{f}}}^{\text{'}}\) ≥ _μ_f and \({\mu }_{{\rm{m}}}^{\text{'}}\) ≥ _μ_m because of pathogenicity. The parameters _η_f

and _η_m are the cure rates for women and men, respectively. Note that the death and cure rates are assumed not to be directly dependent on sexual activity _a_. If _η_j = _η_f = _η_m = 0,

the infection is incurable, meaning that the model is of the susceptible–infected type. The probabilities of transmission per sexual contact are _β_m→f and _β_f→m for male-to-female and

female-to-male transmission, respectively (0 ≤ _β_m→f, _β_f→m ≤ 1). Here, the variables _Θ_f(_t_) and _Θ_m(_t_) stand for the probabilities that the sexual partners of a man and a woman are

infected, respectively. Because a sexual partner with sexual activity _a_ is selected with the probability _aN_f(_t_, _a_)/_N_f(_t_) or _aN_m(_t_, _a_)/_N_m(_t_) and the probability that the

sexual partner is infected is _I_f(_t_, _a_)/_N_f(_t_, _a_) or _I_m(_t_, _a_)/_N_m(_t_, _a_), we have $$\begin{array}{ccc}{\Theta }_{{\rm{f}}}(t) & = & {\int }_{0}^{\infty

}\,\frac{a{I}_{{\rm{f}}}(t,a)}{{N}_{{\rm{f}}}(t)}da,\\ {\Theta }_{{\rm{m}}}(t) & = & {\int }_{0}^{\infty }\,\frac{a{I}_{{\rm{m}}}(t,a)}{{N}_{{\rm{m}}}(t)}da.\end{array}$$ (8) RESULTS

DISEASE-FREE CASE First, we consider the disease-free case (_I_j = _I_f = _I_m = _Θ_f = _Θ_m = 0). The dynamics of population are rewritten as

$$\begin{array}{ccc}\frac{d{S}_{{\rm{j}}}(t)}{dt} & = & B-(\lambda +{\mu }_{{\rm{j}}}){S}_{{\rm{j}}}({\rm{t}}),\\ \frac{{\rm{\partial }}{S}_{{\rm{f}}}(t,a)}{{\rm{\partial }}t} &

= & \lambda (1-\gamma ){S}_{{\rm{j}}}(t){p}_{{\rm{f}}}(a)-{\mu }_{{\rm{f}}}{S}_{{\rm{f}}}(t,a),\\ \frac{{\rm{\partial }}{S}_{{\rm{m}}}(t,a)}{{\rm{\partial }}t} & = & \lambda

\gamma {S}_{{\rm{j}}}(t){p}_{{\rm{m}}}(a)-{\mu }_{{\rm{m}}}{S}_{{\rm{m}}}(t,a).\end{array}$$ (9) There is a stable equilibrium state $${\tilde{S}}_{{\rm{j}}}=\frac{B}{\lambda +{\mu

}_{{\rm{j}}}},\,{\tilde{S}}_{{\rm{f}}}(a)=\frac{\lambda B(1-\gamma )}{{\mu }_{{\rm{f}}}(\lambda +{\mu }_{{\rm{j}}})}{p}_{{\rm{f}}}(a),\,{\tilde{S}}_{{\rm{m}}}(a)=\frac{\lambda B\gamma }{{\mu

}_{{\rm{m}}}(\lambda +{\mu }_{{\rm{j}}})}{p}_{{\rm{m}}}(a),$$ (10) where the tildes over the variables indicate that the values are for the disease-free equilibrium. In this case, from Eq.

(4), we have $$\frac{{k}_{{\rm{f}}}}{{k}_{{\rm{m}}}}=\frac{{\tilde{N}}_{{\rm{m}}}}{{\tilde{N}}_{{\rm{f}}}}=\frac{{\tilde{S}}_{{\rm{m}}}}{{\tilde{S}}_{{\rm{f}}}}=\frac{{\mu }_{{\rm{f}}}\gamma

}{{\mu }_{{\rm{m}}}(1-\gamma )}.$$ (11) LINEARIZATION To derive the basic reproduction number, we linearize Eqs. (1) and (7) near the disease-free case—that is, we consider only the first

order of _I_j, _I_f(_a_), _I_m(_a_), _Θ_f, _Θ_m and replace

\({S}_{{\rm{j}}}={\tilde{S}}_{{\rm{j}}},\,{S}_{{\rm{f}}}(a)={\tilde{S}}_{{\rm{f}}}(a),\,{S}_{{\rm{m}}}(a)={\tilde{S}}_{{\rm{m}}}(a)\) in Eqs. (1) and (7).

$$\begin{array}{ccc}\frac{d{I}_{{\rm{j}}}(t)}{dt} & = & \frac{\alpha (1-\delta ){\mu }_{{\rm{f}}}(\lambda +{\mu }_{{\rm{j}}})}{\lambda (1-\gamma )}{I}_{{\rm{f}}}(t)-({\lambda

}^{{\rm{^{\prime} }}}+{\eta }_{{\rm{j}}}+{\mu }_{j}^{^{\prime} }){I}_{{\rm{j}}}(t),\\ \frac{{\rm{\partial }}{I}_{{\rm{f}}}(t)}{{\rm{\partial }}t} & = & {\lambda }^{{\rm{^{\prime}

}}}(1-\gamma ){I}_{{\rm{j}}}(t)-({\mu }_{{\rm{f}}}^{^{\prime} }+{\eta }_{{\rm{f}}}){I}_{{\rm{f}}}(t)+{\beta }_{{\rm{m}}\to {\rm{f}}}\frac{\lambda B(1-\gamma )}{{\mu }_{{\rm{f}}}(\lambda

+{\mu }_{{\rm{j}}})}{k}_{{\rm{f}}}{\Theta }_{{\rm{m}}}(t),\\ \frac{{\rm{\partial }}{I}_{{\rm{m}}}(t)}{{\rm{\partial }}t} & = & {\lambda }^{{\rm{^{\prime} }}}\gamma

{I}_{{\rm{j}}}(t)-({\mu }_{{\rm{m}}}^{^{\prime} }+{\eta }_{{\rm{m}}}){I}_{{\rm{m}}}(t)+{\beta }_{{\rm{f}}\to {\rm{m}}}\frac{\lambda B\gamma }{{\mu }_{{\rm{m}}}(\lambda +{\mu

}_{{\rm{j}}})}{k}_{{\rm{m}}}{\Theta }_{{\rm{f}}}(t),\\ \frac{{\rm{\partial }}{\theta }_{{\rm{f}}}(t)}{{\rm{\partial }}t} & = & {\lambda }^{{\rm{^{\prime} }}}\frac{{\mu

}_{{\rm{f}}}(\lambda +{\mu }_{{\rm{j}}})}{\lambda B}{I}_{{\rm{j}}}(t)-({\mu }_{{\rm{f}}}^{^{\prime} }+{\eta }_{{\rm{f}}}){\theta }_{{\rm{f}}}(t)+{\beta }_{{\rm{m}}\to

{\rm{f}}}{c}_{{\rm{f}}}{\Theta }_{{\rm{m}}}(t),\\ \frac{{\rm{\partial }}{\theta }_{{\rm{m}}}(t)}{{\rm{\partial }}t} & = & {\lambda }^{{\rm{^{\prime} }}}\frac{{\mu

}_{{\rm{m}}}(\lambda +{\mu }_{{\rm{j}}})}{\lambda B}{I}_{{\rm{j}}}(t)-({\mu }_{{\rm{m}}}^{^{\prime} }+{\eta }_{{\rm{m}}}){\theta }_{{\rm{m}}}(t)+{\beta }_{{\rm{f}}\to

{\rm{m}}}{c}_{{\rm{m}}}{\Theta }_{{\rm{f}}}(t).\end{array}$$ (12) CASE WITHOUT SEXUAL TRANSMISSION Here, we consider a simple case where there is only mother-to-child transmission (_β_m→f = 

_β_f→m = 0). In this case, Eq. (12) is simplified to a three-dimensional system: $$\begin{array}{ccc}\frac{d{I}_{{\rm{j}}}(t)}{dt} & = & \frac{\alpha (1-\delta ){\mu

}_{{\rm{f}}}(\lambda +{\mu }_{{\rm{j}}})}{\lambda (1-\gamma )}{I}_{{\rm{f}}}(t)-({\lambda }^{^{\prime} }+{\eta }_{{\rm{j}}}+{\mu }_{{\rm{j}}}^{^{\prime} }){I}_{{\rm{j}}}(t),\\

\frac{{\rm{\partial }}{I}_{{\rm{f}}}(t)}{{\rm{\partial }}t} & = & {\lambda }^{^{\prime} }(1-\gamma ){I}_{{\rm{j}}}(t)-({\mu }_{{\rm{f}}}^{^{\prime} }+{\eta

}_{{\rm{f}}}){I}_{{\rm{f}}}(t),\\ \frac{{\rm{\partial }}{I}_{{\rm{m}}}(t)}{{\rm{\partial }}t} & = & {\lambda }^{^{\prime} }\gamma {I}_{{\rm{j}}}(t)-({\mu }_{{\rm{m}}}^{^{\prime}

}+{\eta }_{{\rm{m}}}){I}_{{\rm{m}}}(t).\end{array}$$ (13) In this case, we do not need to consider the dynamics of _θ_f(_t_) and _θ_m(_t_) because they do not affect _I_j(_t_), _I_f(_t_) or

_I_m(_t_). We write the linearized system Eq. (13) in the form \(\dot{x}=(T+Q)x\), where matrix _T_ corresponds to transmissions and matrix _Q_ to transitions: $$\begin{array}{rcl}T & =

& (\begin{array}{ccc}0 & \frac{\alpha (1-\delta ){\mu }_{{\rm{f}}}(\lambda +{\mu }_{{\rm{j}}})}{\lambda (1-\gamma )} & 0\\ \frac{\alpha (1-\delta ){\mu }_{{\rm{f}}}(\lambda +{\mu

}_{{\rm{j}}})}{\lambda (1-\gamma )} & 0 & 0\\ \frac{\alpha (1-\delta ){\mu }_{{\rm{f}}}(\lambda +{\mu }_{{\rm{j}}})}{\lambda (1-\gamma )} & 0 & 0\end{array}),\\ Q & =

& (\begin{array}{ccc}-({\lambda }^{\text{'}}+{\eta }_{{\rm{j}}}+{\mu }_{j}^{\text{'}}) & 0 & 0\\ 0 & -\frac{\alpha (1-\delta ){\mu }_{{\rm{f}}}(\lambda +{\mu

}_{{\rm{j}}})}{\lambda (1-\gamma )} & 0\\ 0 & 0 & -({\mu }_{{\rm{f}}}^{\text{'}}+{\eta }_{{\rm{f}}})\end{array}).\end{array}$$ (14) Then, the spectral radius (dominant

eigenvalue) of the next generation matrix −_TQ_−1 gives the reproduction number41,42. After some elementary algebra, we obtain the basic reproduction number for the case without sexual

transmission. $${\alpha }_{{\rm{eff}}}=\frac{\alpha (1-\delta ){\mu }_{{\rm{f}}}(\lambda +{\mu }_{{\rm{j}}}){\lambda }^{\text{'}}}{\lambda ({\mu }_{{\rm{f}}}^{\text{'}}+{\eta

}_{{\rm{f}}})(\lambda ^{\prime} +{\eta }_{{\rm{j}}}+{\mu }_{{\rm{j}}}^{\text{'}})}.$$ (15) Here, the amount _α_eff is the efficient vertical transmission rate. Equation (15) can be

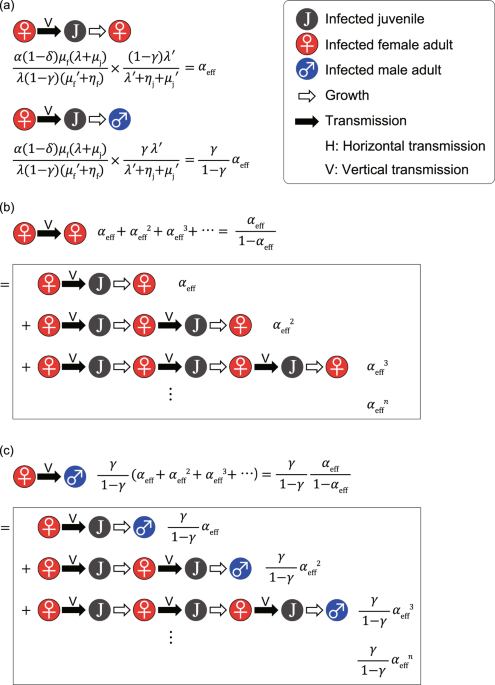
intuitively understood as follows (see Fig. 1a). The number of births per unit of time in the disease-free equilibrium is $$B=\frac{{\mu }_{{\rm{f}}}(\lambda +{\mu }_{{\rm{j}}})}{\lambda

(1-\gamma )}{\tilde{S}}_{{\rm{f}}},$$ (16) as is apparent from Eq. (10). Referring to Eq. (1), the average number of children born to an infected adult women per unit of time is

$$\frac{\alpha (1-\delta ){\mu }_{{\rm{f}}}(\lambda +{\mu }_{{\rm{j}}})}{\lambda (1-\gamma )}.\,$$ (17) Because the average duration for infected adult women is 1/(\({\mu

}_{{\rm{f}}}^{\text{'}}\) + _η_f), the average number of children born to an infected adult woman is $$\frac{\alpha (1-\delta ){\mu }_{{\rm{f}}}(\lambda +{\mu }_{{\rm{j}}})}{\lambda

(1-\gamma )({\mu }_{{\rm{f}}}^{^{\prime} }+{\eta }_{{\rm{f}}})}.\,$$ (18) The probability that a juvenile survives and becomes an adult woman is $$\frac{(1-\gamma )\lambda ^{\prime}

}{\lambda ^{\prime} +{\eta }_{{\rm{j}}}+{\mu }_{{\rm{j}}}^{\text{'}}}.$$ (19) The average number of daughters infected vertically by an infected adult woman is given by the product of

Eqs. (18) and (19), which leads to Eq. (15). The value of _α_eff represents the average number of infected adult daughters of an infected adult woman in a completely susceptible population.

Thus, the epidemic threshold is given by _α_eff = 1. Because _α_ ≤ 1, _λ_′ ≤ _λ_, \({\mu }_{{\rm{j}}}^{\text{'}}\ge {\mu }_{{\rm{j}}}\), \({\mu }_{{\rm{f}}}^{\text{'}}\) ≥ _μ_f,

_η_f ≥ 0, _η_j ≥ 0, and _δ_ ≥ 0, _α_eff is always less than one. Therefore, STIs cannot survive if they spread only by mother-to-child transmission. In the same way (see Fig. 1a), we can

show that the average number of sons infected vertically by an infected adult woman is $$\frac{\gamma }{1-\gamma }\,{\alpha }_{{\rm{eff}}}.$$ (20) As is shown in Fig. 1b, the average number

of adult women infected through consecutive mother-to-child transmissions from an infected adult woman is $$\frac{{\alpha }_{{\rm{eff}}}}{1-{\alpha }_{{\rm{eff}}}}.$$ (21) As is shown in

Fig. 1c, the average number of adults men infected through consecutive mother-to-child transmissions from an infected adult woman is $$\frac{\gamma }{1-\gamma }\,\frac{{\alpha

}_{{\rm{eff}}}}{1-{\alpha }_{{\rm{eff}}}}.$$ (22) TYPE-REPRODUCTION NUMBERS FOR THE GENERAL CASE Here, we calculate the type-reproduction numbers for three compartments. First, to derive the

type-reproduction number for women infected horizontally, we focus on adult women infected through sexual transmission and regard vertical transmissions as transitions. We rewrite the

linearized system Eq. (12) in the form \(\dot{x}\) = (_T_ + _Q_)_x_—that is, $$\begin{array}{ccc}T & = & (\begin{array}{ccccc}0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0

& 0 & {A}_{25}\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & {A}_{45}\\ 0 & 0 & 0 & 0 & 0\end{array}),\\ Q & = &

(\begin{array}{ccccc}-{A}_{11} & {A}_{12} & 0 & 0 & 0\\ {A}_{21} & -{A}_{22} & 0 & 0 & 0\\ {A}_{31} & 0 & -{A}_{33} & {A}_{34} & 0\\ {A}_{41}

& 0 & 0 & -{A}_{44} & 0\\ {A}_{51} & 0 & 0 & {A}_{54} & -{A}_{55}\end{array}).\end{array}$$ (23) Here, for example, _A_11 = _λ_′ + _η_j + \({\mu

}_{{\rm{j}}}^{\text{'}}\) and \({A}_{25}={\beta }_{{\rm{m}}\to {\rm{f}}}\frac{\lambda B(1-\gamma )}{{\mu }_{{\rm{f}}}(\lambda +{\mu }_{{\rm{j}}})}{k}_{{\rm{f}}}\). Calculating the

dominant eigenvalue of −_TQ_−1, we obtain the type-reproduction number for adult women: $${R}_{{\rm{f}}}=\frac{{\beta }_{{\rm{f}}\to {\rm{m}}}{c}_{{\rm{f}}}}{{\mu

}_{{\rm{f}}}^{\text{'}}+{\eta }_{{\rm{f}}}}\frac{{\beta }_{{\rm{m}}\to {\rm{f}}}{c}_{{\rm{m}}}}{{\mu }_{{\rm{m}}}^{\text{'}}+{\eta }_{{\rm{m}}}}+\frac{{\alpha

}_{{\rm{eff}}}}{1-{\alpha }_{{\rm{eff}}}}\frac{{\beta }_{{\rm{f}}\to {\rm{m}}}{k}_{{\rm{f}}}}{{\mu }_{{\rm{f}}}^{\text{'}}+{\eta }_{{\rm{f}}}}\frac{{\beta }_{{\rm{m}}\to

{\rm{f}}}{c}_{{\rm{m}}}}{{\mu }_{{\rm{m}}}^{\text{'}}+{\eta }_{{\rm{m}}}}+\frac{\gamma }{1-\gamma }\frac{{\alpha }_{{\rm{eff}}}}{1-{\alpha }_{{\rm{eff}}}}\frac{{\beta }_{{\rm{m}}\to

{\rm{f}}}{k}_{{\rm{m}}}}{{\mu }_{{\rm{m}}}^{\text{'}}+{\eta }_{{\rm{m}}}}.$$ (24) If _R_f > 1, the STI can spread over the population. Our previous study treating a simpler model

gave a similar formula35, where we called Eq. (24) the basic reproduction number over generations. This metric is the average number of sexually infected adult women generated from a

sexually infected woman in a completely susceptible population. As is shown in Fig. 2b, the first term represents the propagation through only two types of horizontal transmission

(female-to-male and male-to-female); the second term represents the propagation through vertically infected women and these two types of horizontal transmission; and the third term

represents the propagation through vertically infected men and male-to-female horizontal transmission. Note that the first term is dominant in Eq. (24) because _c_m ≫ _k_m and _c_f ≫ _k_f if

_α_eff is not close to one. Second, focusing on adult men infected through sexual transmission, the linearized system Eq. (12) in the form \(\dot{x}\) = (_T_ + _Q_)_x_ is given by

$$\begin{array}{ccc}T & = & (\begin{array}{ccccc}0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & {A}_{34} & 0\\ 0 & 0 & 0

& 0 & 0\\ 0 & 0 & 0 & {A}_{54} & 0\end{array}),\\ Q & = & (\begin{array}{ccccc}-\,{A}_{11} & {A}_{12} & 0 & 0 & 0\\ {A}_{21} & -\,{A}_{22}

& 0 & 0 & {A}_{25}\\ {A}_{31} & 0 & -\,{A}_{33} & 0 & 0\\ {A}_{41} & 0 & 0 & -\,{A}_{44} & {A}_{45}\\ {A}_{51} & 0 & 0 & 0 &

-\,{A}_{55}\end{array}).\end{array}$$ (25) Calculating the dominant eigenvalue of −_TQ_−1, we obtain the type-reproduction number for adult men: $${R}_{{\rm{m}}}=\frac{\frac{{\beta

}_{{\rm{f}}\to {\rm{m}}}{c}_{{\rm{f}}}}{{\mu }_{{\rm{f}}}^{\text{'}}+{\eta }_{{\rm{f}}}}\frac{{\beta }_{{\rm{m}}\to {\rm{f}}}{c}_{{\rm{m}}}}{{\mu }_{{\rm{m}}}^{\text{'}}+{\eta

}_{{\rm{m}}}}+\frac{{\alpha }_{{\rm{eff}}}}{1-{\alpha }_{{\rm{eff}}}}\frac{{\beta }_{{\rm{f}}\to {\rm{m}}}{k}_{{\rm{f}}}}{{\mu }_{{\rm{f}}}^{\text{'}}+{\eta }_{{\rm{f}}}}\frac{{\beta

}_{{\rm{m}}\to {\rm{f}}}{c}_{{\rm{m}}}}{{\mu }_{{\rm{m}}}^{\text{'}}+{\eta }_{{\rm{m}}}}}{1-\frac{\gamma }{1-\gamma }\frac{{\alpha }_{{\rm{eff}}}}{1-{\alpha }_{{\rm{eff}}}}\frac{{\beta

}_{{\rm{m}}\to {\rm{f}}}{k}_{{\rm{m}}}}{{\mu }_{{\rm{m}}}^{\text{'}}+{\eta }_{{\rm{m}}}}}.$$ (26) We can intuitively derive Eq. (26) by enumerating all of the infection paths (see Fig. 

2c). In the case of $$\frac{\gamma }{1-\gamma }\frac{{\alpha }_{{\rm{eff}}}}{1-{\alpha }_{{\rm{eff}}}}\frac{{\beta }_{{\rm{m}}\to {\rm{f}}}{k}_{{\rm{m}}}}{{\mu

}_{{\rm{m}}}^{\text{'}}+{\eta }_{{\rm{m}}}} < 1,$$ Equation (26) is meaningful, representing the average number of sexually infected adult men generated from a sexually infected man

in a completely susceptible population. Otherwise, _R_m diverges to infinity. It is obvious that _R_m > 1 if and only if _R_f > 1. Moreover, we emphasize that _R_m > _R_f if _R_f

> 1. Finally, focusing juveniles infected through mother-to-child transmission, the linearized system Eq. (12) in the form \(\dot{x}\) = (_T_ + _Q_)_x_ is given by $$\begin{array}{ccc}T

& = & (\begin{array}{ccccc}0 & {A}_{12} & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0

& 0 & 0 & 0 & 0\end{array}),\\ Q & = & (\begin{array}{ccccc}-{A}_{11} & 0 & 0 & 0 & 0\\ {A}_{21} & -{A}_{22} & 0 & 0 & {A}_{25}\\

{A}_{31} & 0 & -{A}_{33} & {A}_{34} & 0\\ {A}_{41} & 0 & 0 & -{A}_{44} & {A}_{45}\\ {A}_{51} & 0 & 0 & {A}_{54} &

-{A}_{55}\end{array}).\end{array}$$ (27) Calculating the dominant eigenvalue of −_TQ_−1, we obtain the type-reproduction number for adult men: $${R}_{{\rm{j}}}={\alpha

}_{{\rm{eff}}}(1+\frac{\frac{{\beta }_{{\rm{f}}\to {\rm{m}}}{k}_{{\rm{f}}}}{{\mu }_{{\rm{f}}}^{\text{'}}+{\eta }_{{\rm{f}}}}\frac{{\beta }_{{\rm{m}}\to {\rm{f}}}{c}_{{\rm{m}}}}{{\mu

}_{{\rm{m}}}^{\text{'}}+{\eta }_{{\rm{m}}}}+\frac{\gamma }{1-\gamma }\frac{{\beta }_{{\rm{m}}\to {\rm{f}}}{k}_{{\rm{m}}}}{{\mu }_{{\rm{m}}}^{\text{'}}+{\eta

}_{{\rm{m}}}}}{1-\frac{{\beta }_{{\rm{f}}\to {\rm{m}}}{c}_{{\rm{f}}}}{{\mu }_{{\rm{f}}}^{\text{'}}+{\eta }_{{\rm{f}}}}\frac{{\beta }_{{\rm{m}}\to {\rm{f}}}{c}_{{\rm{m}}}}{{\mu

}_{{\rm{m}}}^{\text{'}}+{\eta }_{{\rm{m}}}}\,}).$$ (28) We can intuitively derive Eq. (28) by enumerating all of the infection paths (see Fig. 2d). In the case of $$\frac{{\beta

}_{{\rm{f}}\to {\rm{m}}}{c}_{{\rm{f}}}}{{\mu }_{{\rm{f}}}^{\text{'}}+{\eta }_{{\rm{}}}}\frac{{\beta }_{{\rm{m}}\to {\rm{f}}}{c}_{{\rm{m}}}}{{\mu }_{{\rm{m}}}^{\text{'}}+{\eta

}_{{\rm{m}}}} < 1,$$ Equation (28) is meaningful because it represents the average number of vertically infected juveniles generated from a vertically infected juvenile in a completely

susceptible population. If sexual transmission is frequent enough (i.e., \(\frac{{\beta }_{{\rm{f}}\to {\rm{m}}}{c}_{{\rm{f}}}}{{\mu }_{{\rm{f}}}^{\text{'}}+{\eta

}_{{\rm{f}}}}\frac{{\beta }_{{\rm{m}}\to {\rm{f}}}{c}_{{\rm{m}}}}{{\mu }_{{\rm{m}}}^{\text{'}}+{\eta }_{{\rm{m}}}} > 1\)), _R_j diverges to infinity. The divergence of _R_j means

that the spread of the STI cannot be stopped even if we eliminate mother-to-child transmission completely. It is obvious that _R_j > 1 if and only if _R_f > 1. The type-reproduction

numbers in Eqs. (24), (26) and (28) are independent of the number of births per unit of time _B_. Thus, regardless of the details of the birth process, these formulas are always valid for

the equilibrium. Without mother-to-child transmission (_α_ = 0 or _α_eff = 0), we obtain $${R}_{{\rm{f}}}={R}_{{\rm{m}}}=\frac{{\beta }_{{\rm{f}}\to {\rm{m}}}{c}_{{\rm{f}}}}{{\mu

}_{{\rm{f}}}^{\text{'}}+{\eta }_{{\rm{f}}}}\frac{{\beta }_{{\rm{m}}\to {\rm{f}}}{c}_{{\rm{m}}}}{{\mu }_{{\rm{m}}}^{\text{'}}+{\eta }_{{\rm{m}}}},$$ (29) which agrees with May and

Anderson’s result for heterosexual transmission, where they presented \({R}_{0}=\sqrt{{\beta }_{{\rm{f}}\to {\rm{m}}}{c}_{{\rm{f}}}{\beta }_{{\rm{m}}\to {\rm{f}}}{c}_{{\rm{m}}}}\) when _η_f 

= _η_m = 0 and \({\mu }_{{\rm{f}}}^{\text{'}}\) = \({\mu }_{{\rm{m}}}^{\text{'}}\) = 121. In this case, _R_f and _R_m coincide with the square of the conventional _R_0. GRAPHICAL

ANALYSIS In Fig. 3, we show the relationship between the infection rate (vertical and horizontal) and the three type of reproduction numbers. Here, we set _k_f, _k_m = 0.8, _c_f, _c_m = 20,

_μ_f, \({\mu }_{{\rm{f}}}^{\text{'}}\), _μ_m, \({\mu }_{{\rm{m}}}^{\text{'}}\), _μ_j, \({\mu }_{{\rm{j}}}^{\text{'}}\) = 1/50, _η_f, _η_m, _η_j =0, _δ_ = 0, and _λ_ = _λ_′ = 

1/15, and then _α_eff = _α_. When the vertical transmission rate is low or _β_m→f≪_β_f→m, there is almost no difference between _R_f and _R_m. Otherwise, when STI is not widespread, the

type-reproduction number of females exceeds that of males (i.e., 1 > _R_f > _R_m); when the STI has already spread, the type-reproduction number of males is larger than that of females

(i.e., _R_m > _R_f > 1). This result means that if an efficient vaccine for the STI exists, vaccination of females is more effective for containment of the STI than vaccination of

males because herd immunity would be possible at vaccination rates above 1 − 1/_R_f for females or 1 − 1/_R_m for males. As far as the type-reproduction numbers are concerned, the effective

increase in the cure rate _η_m is equivalent to the effective decrease in _β_m→f. Similarly, the increase in mortality \({\mu }_{{\rm{m}}}^{\text{'}}\) due to the STI is equivalent to

the decrease in _β_m→f. On the other hand, the increase in cure rate _η_f is equivalent to the decrease in both _β_f→m and _α_eff, and the increase in mortality \({\mu

}_{{\rm{f}}}^{\text{'}}\) is equivalent to the decrease in both _β_f→m and _α_eff. Equations (24), (26) and (28) do not explicitly include the mortality rate of juveniles (_μ_j,\({\mu

}_{{\rm{j}}}^{\text{'}}\)), but the type-reproduction numbers depend on _μ_j and \({\mu }_{{\rm{j}}}^{\text{'}}\) through the efficient vertical transmission rate _α_eff, which

decreases when \({\mu }_{{\rm{j}}}^{\text{'}}\) increases. Keeping _c_f/_k_f (_c_m/_k_m) constant, increasing _k_f (_k_m) corresponds to increasing _β_f→m (_β_m→f). DISCUSSION In this

article, we have presented a compartment model of STIs, considering both mother-to-child transmission and sexual transmission. The proposed model is of major importance because it takes into

account the heterogeneity of sexual contacts, adult mortality from infection, infant mortality caused by mother-to-child transmission, infertility or stillbirth caused by infection, and

recovery with treatment. Our model derives analytical formulas for the type-reproduction numbers _R_f, _R_m, and _R_j. Because these metrics give the same epidemic threshold, it is

convenient to use the simplest formula, Eq. (24). Equation (24) coincides qualitatively with the basic production number over generations that we proposed in previous work35. The model

proposed here allows us to understand how the various effects of mother-to-child transmission on juveniles will change the epidemic threshold. It should be emphasized that all effects of

STIs on the juvenile period before reproductive age are expressed mathematically in _α_eff. For example, infant mortality and various disturbances to growth reduce _α_eff. Because _α_eff is

not in the dominant term in Eq. (24), _α_eff does not strongly affect the epidemic threshold. In other words, the spreading efficiency of STIs will not be strongly altered even if various

problems in the juvenile stage (i.e., mortality or stillbirth) are solved. In sum, we suggest that the heterogeneity of sexual contacts highly contributes to the spread of STIs, and

mother-to-child transmission may work as an auxiliary infection route, contributing to the survival of STIs. This fact was derived from the mathematical analysis and is consistent with our

previous work, which did not consider mortality from STIs35. The analytical formulas for type-reproduction numbers can provide us with important insight into strategies to prevent the

spreading of STIs. If there was an efficient vaccine, herd immunity would be possible at vaccination rates above 1 − 1/_R_f for women or 1 − 1/_R_m for men. _R_m > _R_f, as was shown

above, because of mother-to-child transmission; therefore, our result means that if the number of vaccines and the amount of funds are limited, it is more efficient to concentrate the

vaccine in women only. For example, in many countries, publicly funded HPV immunization programs target young adolescent girls, who are at the border between the juvenile period and

adulthood43. According to our results, this intensive vaccination investment in young girls makes sense mathematically. To apply our results quantitatively to actual STIs, we need to

estimate the model parameters using clinical epidemiological and demographic data on sexual behavior. However, it is difficult to estimate the infection rate (i.e., _β_m→f, _β_f→m, and _α_)

and mortality rate (i.e., \({\mu }_{{\rm{j}}}^{\text{'}}\), \({\mu }_{{\rm{f}}}^{\text{'}}\), and \({\mu }_{{\rm{m}}}^{\text{'}}\)) of specific individual STIs because people

frequently have more than one STI at the same time44. In addition, the data on the distribution of human sexual activity are insufficient45. Nevertheless, we are able to form some

preliminary qualitative conclusions. Many STIs have serious fetal consequences, such as TORCH infections46,47, which include toxoplasmosis, other diseases (syphilis, varicella-zoster,

parvovirus), rubella, cytomegalovirus, and herpes infections. Most TORCH infections cause mild maternal morbidity and have serious fetal consequences, and the treatment of maternal

infections often has no impact on fetal outcomes; thus, the recovery rate _η_j for juveniles is nearly zero47. For incurable STIs such as HIV, HSV, HPV, HTLV-1, and antibiotic-resistant

STIs, the proposed model is a susceptible–infected model (_η_j = _η_f = _η_m = 0). For recovery with treatment, the recovery rates depend on the medical systems and treatment strategy. For

example, it is possible that infected women are less aware of their infections than are infected men with the same STIs, _η_f < _η_m because the treatment of infected women and is not

promoted to the same extent as is the treatment of infected men48,49. In addition, some STIs may inhibit children’s growth even when the infections are not fatal. For example, HSV can bring

on central nervous system disorder30, and cytomegalovirus can lead to long-term neurological sequelae including unilateral and bilateral sensorineural hearing loss, mental retardation,

cerebral palsy, and impaired vision from chorioretinitis50,51,52. In these cases, the maturing rate _λ_' for infected juveniles is lower than the maturing rate _λ_ for susceptible

juveniles. The model proposed here did not consider some important factors that are related to the diffusion of STIs. First, we neglected some routes of transmission, such as needle

sharing53,54,55 and blood transfusion56, because these routes were rare in ancient times and there are many efforts to reduce them now57,58. Moreover, only a few STIs are known to be

transmitted by mosquito bites59. Here, we focused on understanding the diffusion contribution of sexual and mother-to-child transmission. Second, our model assumed that sexual contacts are

well mixed, and the effects of sex workers55, marital status and age structure were not taken into account. The presence of sex workers will increase the heterogeneity of sexual contact.

Marital status will affect the infection dynamics of STIs because marriage yields sustained sexual activity with a specific partner60. The age structure also will influence the diffusion of

STIs61. Sexual transmission tends to occur among people of the same generation, whereas mother-to-child transmission propagates infections across generations; thus, our model may slightly

underestimate the contribution of mother-to-child transmission. Third, homosexual contact was not considered here, although homosexual transmission is important, especially for the spread

not of only HIV but also of HBV, syphilis etc.62. In this article, our aim was to understand the complex infection dynamics, simultaneously considering both unequal sexual transmission rates

between males and females and mother-to-child transmission. If we also considered homosexual and bisexual networks, the infection dynamics would become extremely complicated. Thus, here, we

have not discussed the spread of STIs through homosexual networks, such as men who have sex with men. Fourth, we have assumed that sexual activity is not inherited and does not depend on

whether an individual is infected or not. In addition, we did not consider the correlation between sexual activity and fecundity. Constructing a model that takes into account the inheritance

of sexual activity may reproduce the heterogeneous distribution of this variable. These limitations should be addressed in future research. In conclusion, the comprehensive model proposed

in this article can clarify the complex transmission of STIs. This model is prospective: It is meant to predict the spread of various STIs. We derived analytical formulas for three

type-reproduction numbers, _R_f, _R_m, and _R_j, and elucidated the relationships among them. However, the quantitative evaluation of these metrics for actual STIs remains a topic for future

research. The quantitative application of our model has the potential to clarify which kinds of countermeasures will be effective in combating STIs. DATA AVAILABILITY The authors declare

that all data supporting the findings of this study are available within the article or from the corresponding author upon reasonable request. REFERENCES * Oriel, J. D. The Scars of Venus: A

History of Venereology (Springer-Verlag, 1994). * Waugh, M. History of sexually transmitted infections. In _Sexually Transmitted Infections and Sexually Transmitted Diseases_ (eds Gross, G.

& Tyring, S. K.) 3–11 (Springer-Verlag, 2011). * Gewirtzman, A., Bobrick, L., Conner, K. & Tyring, S. K. Epidemiology of sexually transmitted infections. In _Sexually Transmitted

Infections and Sexually Transmitted Diseases_ (eds Gross, G. & Tyring, S. K.) 13–34 (Springer-Verlag, 2011). * World Health Organization. _Global Strategy for the Prevention and Control

of Sexually Transmitted Infections, 2006–2015: Breaking the Chain of Transmission_ (WHO Press, 2007). * Erbelding, E. & Quinn, T. C. The impact of antimicrobial resistance on the

treatment of sexually transmitted diseases. _Inf. Dis. Clin. North Am._ 11, 889–903 (1997). Article  CAS  Google Scholar  * Ison, C. A. Antimicrobial resistance in sexually transmitted

infections in the developed world: implications for rational treatment. _Curr. Opin. Infect. Dis._ 25, 73–78 (2012). Article  CAS  PubMed  Google Scholar  * McElligott, K. A. Mortality from

sexually transmitted diseases in reproductive-aged women: United States, 1999–2010. _Am. J. Public Health_ 104, e101–e105 (2014). Article  PubMed  PubMed Central  Google Scholar  * World

Health Organization. _Global Health Observatory (GHO) data_, https://www.who.int/gho/hiv/en/ (Accessed March 12, 2019). * UNAIDS. _Global HIV & AIDS statistics – 2018 fact sheet_,

http://www.unaids.org/en/resources/fact-sheet (Accessed April 4, 2019). * Stanaway, J. D. _et al_. The global burden of viral hepatitis from 1990 to 2013: findings from the Global Burden of

Disease Study 2013. _Lancet_ 388, 1081–1088 (2016). Article  PubMed  PubMed Central  Google Scholar  * Lowy, D. R. & Schiller, J. T. Reducing HPV-associated cancer globally. _Cancer

Prev. Res. (Phila)_ 5, 18–23 (2012). Article  Google Scholar  * Denny, L. Cervical cancer: prevention and treatment. _Discov. Med._ 14, 125–131 (2012). PubMed  Google Scholar  * Bray, F. _et

al_. Global cancer statistics 2018: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. _CA: Cancer J. Clin._ 68, 394–424 (2018). Google Scholar  *

Chesson, H. W., Kirkcaldy, R. D., Gift, T. L., Owusu-Edusei, K. Jr. & Weinstock, H. S. Ciprofloxacin resistance and gonorrhea incidence rates in 17 cities, United States, 1991–2006.

_Emerg. Infect. Dis._ 20, 612–619 (2014). Article  CAS  PubMed  PubMed Central  Google Scholar  * Chesson, H. W., Mayaud, P. & Aral, S. O. Sexually transmitted infections: impact and

cost-effectiveness of prevention. In _Major Infectious Diseases, 3rd ed_. (eds Holmes, K. K., Bertozzi, S., Bloom, B. R. & Jha, P.) 203–232 (World Bank, 2017). * Garnett, G. An

introduction to mathematical models in sexually transmitted disease epidemiology. _Sex. Transm. Infect._ 78, 7–12 (2002). Article  CAS  PubMed  PubMed Central  Google Scholar  * Anderson, R.

M. & May, R. M. _Infectious Diseases of Humans: Dynamics and Control_ (Oxford University Press, 1991). * Cooke, K. L. & Yorke, J. A. Some equations modelling growth processes and

gonorrhea epidemics. _Math. Biosci._ 16, 75–101 (1973). Article  MathSciNet  MATH  Google Scholar  * Anderson, R. M., Medley, G. F., May, R. M. & Johnson, A. M. A preliminary study of

the transmission dynamics of the human immunodeficiency virus (HIV), the causative agent of AIDS. IMA. _J. Math. Med. Biol._ 3, 229–263 (1986). Article  MathSciNet  CAS  MATH  Google Scholar

  * Anderson, R. M. _et al_. The invasion, persistence and spread of infectious diseases within animal and plant communities. _Phil. Trans. R. Soc. B._ 314, 533–570 (1986). Article  ADS  CAS

  PubMed  Google Scholar  * May, R. M. & Anderson, R. M. Transmission dynamics of HIV infection. _Nature_ 326, 137–142 (1987). Article  ADS  CAS  PubMed  Google Scholar  * Anderson, R.

M. & Garnett, G. P. Mathematical models of the transmission and control of sexually transmitted diseases. _Sex. Transm. Dis._ 27, 636–643 (2000). Article  CAS  PubMed  Google Scholar  *

Liljeros, F., Edling, C. R., Amaral, L. A., Stanley, H. E. & Aberg, Y. The web of human sexual contacts. _Nature_ 411, 907–908 (2001). Article  ADS  CAS  PubMed  Google Scholar  *

Schneeberger, A. _et al_. Scale-free networks and sexually transmitted diseases: a description of observed patterns of sexual contacts in Britain and Zimbabwe. _Sex. Transm. Dis._ 31,

380–387 (2004). Article  PubMed  Google Scholar  * Latora, V. _et al_. Network of sexual contacts and sexually transmitted HIV infection in Burkina Faso. _J. Med. Virol._ 78, 724–729 (2006).

Article  PubMed  Google Scholar  * Ito, H., Tamura, K., Wada, T., Yamamoto, T. & Morita, S. Is the network of heterosexual contact in Japan scale free? _PLoS One._ 14, e0221520 (2019).

Article  PubMed  PubMed Central  Google Scholar  * Yamamoto, T. _et al_. Inhibitory activity in saliva of cell-to-cell transmission of human T-cell lymphotropic virus type 1 _in vitro_:

evaluation of saliva as an alternative source of transmission. _J. Clin. Microbiol._ 33, 1510–1515 (1995). CAS  PubMed  PubMed Central  Google Scholar  * Tajima, K. The T- and B-Cell

Malignancy Study Group. The 4th nation‐wide study of adult T‐cell leukemia/lymphoma (ATL) in Japan: estimates of risk of ATL and its geographical and clinical features. _Int. J. Cancer._ 45,

237–243 (1990). Article  CAS  PubMed  Google Scholar  * Eriksen, E. M. _et al_. Lack of association between hepatitis B birth immunization and neonatal death: a population-based study from

the vaccine safety datalink project. _Pediatr. Infect. Dis. J._ 23, 656–662 (2004). Article  PubMed  Google Scholar  * Whitley, R. J. _et al_. Vidarabine therapy of neonatal herpes simplex

virus infection. _Pediatrics_ 66, 495–501 (1980). CAS  PubMed  Google Scholar  * Gust, D. A., Levine, W. C., St Louis, M. E., Braxton, J. & Berman, S. M. Mortality associated with

congenital syphilis in the United States, 1992–1998. _Pediatrics_ 109, E79 (2002). Article  PubMed  Google Scholar  * Kapogiannis, B. G. _et al_. Mortality trends in the US Perinatal AIDS

Collaborative Transmission Study (1986–2004). _Clin. Infect. Dis._ 53, 1024–1034 (2011). Article  PubMed  PubMed Central  Google Scholar  * Bristow, B. N., O’Keefe, K. A., Shafir, S. C.

& Sorvillo, F. J. Congenital cytomegalovirus mortality in the United States, 1990–2006. _PLoS Negl. Trop. Dis._ 5, e1140 (2011). Article  PubMed  PubMed Central  Google Scholar  *

Sampath, A., Maduro, G. & Schillinger, J. A. Infant death: Due to herpes simplex virus, congenital syphilis, and HIV in New York City. _Pediatrics_ 137, e20152387 (2016). Article  PubMed

  Google Scholar  * Ito, H., Yamamoto, T. & Morita, S. Demography of sexually transmitted infections with vertical transmission. _Appl. Math. Comput._ 348, 363–370 (2019). MathSciNet 

Google Scholar  * Roberts, M. G. & Heesterbeek, J. A. P. A new method for estimating the effort required to control and infectious disease. _Proc. Biol. Sci._ 270, 1359–1364 (2003).

Article  CAS  PubMed  PubMed Central  Google Scholar  * Heesterbeek, J. A. P. & Roberts, M. G. The type-reproduction number T in models for infectious disease control. _Math. Biosci._

206, 3–10 (2007). Article  MathSciNet  CAS  PubMed  MATH  Google Scholar  * Castellano, C. & Pastor-Satorras, R. Thresholds for epidemic spreading in networks. _Phys. Rev. Lett._ 105,

218701 (2010). Article  ADS  PubMed  CAS  Google Scholar  * Caldarelli, G., Capocci, A., De Los Rios, P. & Muñoz, M. A. Scale-Free Networks from Varying Vertex Intrinsic Fitness. _Phys.

Rev. Lett._ 89, 258702 (2002). Article  ADS  CAS  PubMed  Google Scholar  * Morita, S. Crossovers in scale-free networks on geographical space. _Phys. Rev. E._ 73, 035104R (2006). Article 

ADS  CAS  Google Scholar  * Diekmann, O., Heesterbeek, J. A. P. & Metz, J. A. J. On the definition and the computation of the basic reproduction ratio R0 in models for infectious disease

in heterogeneous populations. _J. Math. Biol._ 28, 365–382 (1990). Article  MathSciNet  CAS  PubMed  MATH  Google Scholar  * Diekmann, O., Heesterbeek, J. A. P. & Metz, M. G. The

construction of next-generation matrices for compartmental epidemic models. _J. R. Soc. Interface_ 7, 873–885 (2010). Article  CAS  PubMed  Google Scholar  * Bruni, L. _et al_. Global

estimates of human papillomavirus vaccination coverage by region and income level: a pooled analysis. _Lancet Glob Health._ 4, e453–463 (2017). Article  Google Scholar  * Pakianathan, M. R.,

Ross, J. D. & McMillan, A. Characterizing patients with multiple sexually acquired infections: a multivariate analysis. _Int. J. STD AIDS_ 7, 359–361 (1996). Article  CAS  PubMed 

Google Scholar  * Aral, S. O. & Ward, H. Behavioral convergence: implications for mathematical models of sexually transmitted infection transmission. J. Infect. _Dis._ 210(Suppl 2),

S600–S604 (2014). Google Scholar  * Fine, J. D. & Arndt, K. A. The TORCH syndrome: a clinical review. _J. Am. Acad. Dermatol._ 12, 697–706 (1985). Article  CAS  PubMed  Google Scholar  *

Stegmann, B. J. & Carey, J. C. TORCH infections: toxoplasmosis, other (syphilis, varicella-zoster, parvovirus B19), rubella, cytomegalovirus (CMV), and herpes infections. _Curr. Womens

Health Rep._ 2, 253–258 (2002). PubMed  Google Scholar  * Voeten, H. A. _et al_. Gender differences in health care-seeking behavior for sexually transmitted diseases: a population-based

study in Nairobi, Kenya. _Sex. Transm. Dis._ 31, 265–272 (2004). Article  PubMed  Google Scholar  * Adeyemi, E. O. Gender inequities in sexually transmitted infections: implications for HIV

infection and control in Lagos State, Nigeria. _Infect. Dis. Rep._ 3, e7 (2011). Article  PubMed  PubMed Central  Google Scholar  * Boppana, S. B., Pass, R. F., Britt, W. J., Stagno, S.

& Alford, C. A. Symptomatic congenital cytomegalovirus infection: neonatal morbidity and mortality. _Prediatr. Infect. Dis. J._ 11, 93–99 (1992). Article  CAS  Google Scholar  * Boppana,

S. B., Fowler, K. B., Britt, W. J., Stagno, S. & Pass, R. F. Symptomatic congenital cytomegalovirus infection in infants born to mothers with preexisting immunity to cytomegalovirus.

_Pediatrics_ 104, 55–60 (1999). Article  CAS  PubMed  Google Scholar  * Boppana, S. B., Ross, S. A. & Fowler, K. B. Congenital cytomegalovirus infection: clinical outcome. _Clin. Infect.

Dis._ 15, S178–S181 (2013). Article  Google Scholar  * Vlahov, D. & Junge, B. The role of needle exchange programs in HIV prevention. _Public Health Rep._ 113(Suppl 1), 75–80 (1998).

PubMed  PubMed Central  Google Scholar  * Lowndes, C. M., Alary, M. & Platt, L. Injection drug use, commercial sex work, and the HIV/STI epidemic in the Russian Federation. _Sex. Transm.

Dis._ 30, 46–48 (2003). Article  PubMed  Google Scholar  * Mashkilleyson, N. & Lazarus J. V. HIV in Eastern Europe. In _Sexually Transmitted Infections and Sexually Transmitted

Diseases_ (eds Gross, G. & Tyring, S. K.) 319–336 (Springer-Verlag, 2011). * Bihl, F., Castelli, D., Marincola, F., Dodd, R. Y. & Brander, C. Transfusion-transmitted infections. _J.

Transl. Med._ 5, 25 (2007). Article  PubMed  PubMed Central  Google Scholar  * Hurley, S. F., Jolley, D. J. & Kaldor, J. M. Effectiveness of needle-exchange programmes for prevention of

HIV infection. _Lancet._ 349, 1797–1800 (1997). Article  CAS  PubMed  Google Scholar  * Burr, C. K. _et al_. Integrating health and prevention services in syringe access programs: a strategy

to address unmet needs in a high-risk population. _Public Health Rep._ 129(Suppl 1), 26–32 (2014). Article  PubMed  PubMed Central  Google Scholar  * Gao, D. _et al_. Prevention and control

of Zika as a mosquito-borne and sexually transmitted disease: a mathematical modeling analysis. _Sci. Rep._ 6, 28070 (2016). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  *

Taylor, E. M., Adimora, A. A. & Schoenbach, V. J. Marital status and sexually transmitted infections among African Americans. _J. Fam. Issues_ 31, 1141–1165 (2010). Article  Google

Scholar  * Li, J. & Brauer, F. Continuous-time age-structured models in population dynamics and epidemiology. In _Mathematical Epidemiology_. (eds Brauer, F., van den Driessche, P. &

Wu, J.) 205–227 (Springer, 2008). * Blythe, S. P. & Anderson, R. M. Heterogeneous sexual activity models of HIV transmission in male homosexual populations. _IMA J. Math. Appl. Med.

Biol._ 4, 237–260 (1988). Article  MathSciNet  MATH  Google Scholar  Download references ACKNOWLEDGEMENTS This work was supported by the Japan Society for the Promotion of Science,

Grants-in-Aid for Scientific Research (grants 17J06741 and 17H04731 to H.I., 17H04659 to T.Y., and 18K03453 to S.M.), research grants from the Japan Prize Foundation and the Pfizer Health

Research Foundation to HI, and the Joint Usage/Research Center on Tropical Disease, Institute of Tropical Medicine, Nagasaki University (2019-Ippan-23) and the Japan Science and Technology

Agency Crest to SM. We thank Jin Yoshimura and Takayuki Wada for valuable feedback and discussions. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of International Health and

Medical Anthropology, Institute of Tropical Medicine, Nagasaki University, Nagasaki, 852-8523, Japan Hiromu Ito & Taro Yamamoto * Department of Environmental Sciences, Zoology,

University of Basel, 4051, Basel, Switzerland Hiromu Ito * Department of Mathematical and Systems Engineering, Shizuoka University, Hamamatsu, Shizuoka, 432-8561, Japan Satoru Morita *

Department of Environment and Energy Systems, Graduate School of Science and Technology, Shizuoka University, Hamamatsu, Shizuoka, 432-8561, Japan Satoru Morita Authors * Hiromu Ito View

author publications You can also search for this author inPubMed Google Scholar * Taro Yamamoto View author publications You can also search for this author inPubMed Google Scholar * Satoru

Morita View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS H.I., T.Y. and S.M. conceived the study and wrote the manuscript. H.I. and S.M.

constructed the mathematical model. T.Y. and S.M. assisted in the interpretation of the results. H.I. and S.M. generated the figures. H.I., T.Y. and S.M. revised the references and data.

CORRESPONDING AUTHOR Correspondence to Satoru Morita. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer

Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative

Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the

original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in

the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended

use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit

http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Ito, H., Yamamoto, T. & Morita, S. The type-reproduction number of sexually

transmitted infections through heterosexual and vertical transmission. _Sci Rep_ 9, 17408 (2019). https://doi.org/10.1038/s41598-019-53841-8 Download citation * Received: 06 June 2019 *

Accepted: 06 November 2019 * Published: 22 November 2019 * DOI: https://doi.org/10.1038/s41598-019-53841-8 SHARE THIS ARTICLE Anyone you share the following link with will be able to read

this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative