Why scanning tunneling spectroscopy of sr2ruo4 sometimes doesn’t see the superconducting gap

ABSTRACT Scanning tunneling spectroscopy (STS) and scanning tunneling microscopy (STM) are perhaps the most promising ways to detect the superconducting gap size and structure in the

canonical unconventional superconductor Sr2RuO4 directly. However, in many cases, researchers have reported being unable to detect the gap at all in STM conductance measurements. Recently,

an investigation of this issue on various local topographic structures on a Sr-terminated surface found that superconducting spectra appeared only in the region of small nanoscale canyons,

corresponding to the removal of one RuO surface layer. Here, we analyze the electronic structure of various possible surface structures using first principles methods, and argue that bulk

conditions favorable for superconductivity can be achieved when removal of the RuO layer suppresses the RuO4 octahedral rotation locally. We further propose alternative terminations to the

most frequently reported Sr termination where superconductivity surfaces should be observed. SIMILAR CONTENT BEING VIEWED BY OTHERS OBSERVATION OF YU-SHIBA-RUSINOV-LIKE STATES AT THE EDGE OF

CRBR3/NBSE2 HETEROSTRUCTURE Article Open access 22 November 2024 SPECTROSCOPIC SIGNATURE OF OBSTRUCTED SURFACE STATES IN SRIN2P2 Article Open access 22 May 2023 EVIDENCE OF TOPOLOGICAL

BOUNDARY MODES WITH TOPOLOGICAL NODAL-POINT SUPERCONDUCTIVITY Article 25 October 2021 INTRODUCTION The superconducting order parameter of Sr2RuO41,2,3,4 is thought to be of unconventional

nature, but has proven unexpectedly difficult to identify. Soon after its discovery in 1994, it was proposed as a promising candidate for a chiral _p_-wave, spin triplet superconductor by

analogy to superfluid 3He-A, based in particular on early evidence from NMR5. Muon-spin rotation6 and Kerr effect7 measurements suggested intrinsic time-reversal symmetry (TRS) breaking8

below _T__c_, consistent with this proposal. Thermodynamic measurements provided clear evidence for low-energy quasiparticle states, however, suggesting the existence of gap nodes or deep

minima9,10,11,12. In 2019, the authors of ref. 13 challenged the chiral _p_-wave paradigm with in-plane 17O nuclear magnetic resonance measurements that found a significant decrease in the

Knight shift below _T_c13,14. Spin-triplet pairing was then definitively ruled out by comparison to the change of the entropy from earlier specific heat experiments15. These measurements

were accompanied by observations of shifts in the elastic constants16,17 together with experiments under strain18 suggesting a two component nature of the order parameter. All these results

led to renewed theoretical attempts to calculate the superconducting ground state of Sr2RuO4 within a spin singlet picture19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37, leading to

a variety of proposals, including the even-parity 1D irreducible representation \({B}_{1g}({d}_{{x}^{2}-{y}^{2}})\), multi-component orders such as

\({d}_{{x}^{2}-{y}^{2}}+i{g}_{xy({x}^{2}-{y}^{2})}\) and \(s^{\prime} +i{d}_{xy}\), as well as the 2D irreducible representation _E_1_g_(_d__x__z_ + _i__d__y__z_). A two-component state is

thought to be required to explain ultrasound measurements16,17 and recent _μ_SR experiments under strain18 (see however refs. 36,38), but other recent measurements provide evidence for a

single order parameter component39,40. While the experiments cited above and many others provide indirect evidence in support of one superconducting pairing channel or another, the

community’s ability to definitively identify the order parameter is severely hindered by the difficulty of making _direct_ measurements of the superconducting gap over the Fermi surface. The

extremely small gap (∣Δ∣ ≤ 350 _μ_eV)41,42 of the superconducting order parameter Δ(K) in Sr2RuO4 means that angle-resolved photoemission (ARPES) experiments do not currently have the fine

energy and momentum resolution to detect spectral features reflecting the gap. Scanning tunneling spectroscopy experiments that detect Bogoliubov quasiparticle interference (BQPI) provide,

on the other hand, good momentum resolution and finer energy resolution in the best circumstances. Recently, the BQPI technique was used for Sr2RuO442. This analysis, based on comparison

with a simple lattice calculation of the joint density of states, suggested a \({d}_{{x}^{2}-{y}^{2}}\) superconducting gap symmetry for Sr2RuO4. A somewhat more sophisticated calculation

involving first-principles surface Wannier functions was also compared to the same data43, but more than one gap function appeared to fit nearly equally well. Nevertheless, BQPI appears to

be the best possibility of “directly” measuring the superconducting gap in this canonical unconventional superconductor. There is however one enduring, poorly understood puzzle regarding

scanning tunneling spectroscopy (STS) and scanning tunneling microscopy (STM) studies of superconducting Sr2RuO4. While some STS/STM measurements have reported signatures of

superconductivity on the surface of Sr2RuO4 for many years41,42,44, others on apparently equivalent surfaces under similar conditions are unable to detect any gap at all45,46,47,48.

Interestingly, superconductivity was reported in samples with regions of RuO2 termination41, while most of the investigations where superconductivity was not detected were performed on the

the usual SrO termination. Recognizing that this question was an important one to resolve in order to properly interpret STS/STM data on the Sr2RuO4 surface, the authors of refs. 49,50,51

performed a systematic study of local STS/STM conductance spectra at several distinct types of local topographic structures on the surface with different termination layers. They found that

superconducting spectra with coherence peaks appeared only in the region of small nanoscale “pits” on the surface, corresponding to the removal of one RuO surface layer. Since the Sr2RuO4

surface is thought to be reconstructed in a pattern of RuO6 octahedral rotation similar to that of bulk Sr3Ru2O7 and calcium doped bulk Sr2RuO447,52,53,54,55, it is natural to ask if the

atomic layer on the surface might be electronically different to that placed immediately underneath it, such that conditions favorable to superconductivity are “masked”. As stated in refs.

47,53, superconductivity is not observed although the surfaces are pristine. In other words, is it possible that superconductivity in Sr2RuO4 can never be observed on a hypothetical perfect

but reconstructed Sr2RuO4 surface, but is only revealed when such pits form? Or, alternatively, are there other possible Sr2RuO4 surfaces, with little reconstruction compared to the bulk

case, that might actually reveal the superconducting gap as in the bulk? Here we investigate the plausibility of such a scenario by performing first-principles-based electronic structure

simulations. RESULTS In the following we examine how the surface termination and rotation angles of the RuO6 octahedra in Sr2RuO4 affect its electronic structure employing density functional

theory (DFT), which has provided reliable results for the Fermi-liquid normal state of bulk Sr2RuO456. We determine the optimal rotation angle depending on the type of termination, and

perform large-scale canyon structure simulations to investigate the above scenario predicting that pits in the surface allow to observe signatures of bulk physics. To understand better the

changes induced by the octahedral rotation in Sr2RuO4 we first focus on a Sr-terminated monolayer for which we consider different RuO6 rotation angles. The effect of the rotation on the band

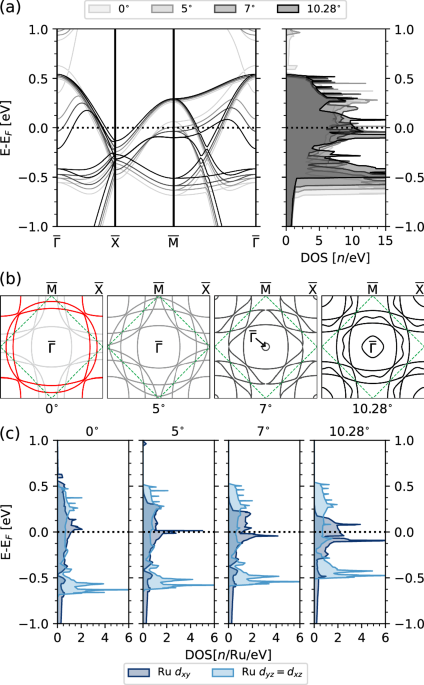
structure, Fermi surface, total density of states (DOS) and projected DOS is visualized in Fig. 1 and is in agreement with previous results57 as well as recently reported ARPES

measurements58, with the exception that the pocket opening around the \({\bar{\Gamma}}\) point is at smaller values of the octahedral rotation - which is a known shortcoming of DFT57. As

shown in Fig. 1, the octahedral rotation pushes the van-Hove singularity (vHs) – located in the _d__x__y_ orbital – from a position above the Fermi level at 0∘ rotation, as in the bulk

case21,28,56,59,60,61, to a position below the Fermi level at the optimal octahedral rotation value. As a consequence of this, the _d__x__y_-orbital dominated Fermi surface section near the

\(\bar{M}\)-point vanishes (see the band structure and Fermi surface plotted in Fig. 1a, b. Furthermore, a pocket at the \(\bar{\Gamma }\) point in the _d__x__y_ orbital opens up at

approximately 6∘ octahedral rotation. This feature has been identified as a source of suppressed superconductivity in a recent theoretical investigation by some of the authors62 by

performing functional renormalization group (FRG) calculations for wannierized tight-binding models for the surface of Sr2RuO4. In the same spirit and motivated by recent strain dependent

experiments18,40,63,64,65 indicating a strong effect of the vHs position on _T__c_, we investigate different possible realizations of surfaces with the aim to recover bulk-like behavior in

the surface layer, which would support the scenario that the detection of superconductivity on the surface is directly related to the surface having similar electronic properties as the

bulk. By cleaving such surfaces, surface sensitive probes, like STS, as mentioned in the introduction, can then be utilized to image the superconducting order parameter. We consider four

different charge neutral surface configurations in Sr2RuO4 including the experimentally realized Sr termination47, a Ru termination, and a 2Sr termination (see Fig. 2a). While the latter two

terminations, to our knowledge, have not yet been reported as a clean surface, our findings indicate that trying to cleave or grow these is highly desirable in order to restore bulk physics

on the surface. As a fourth configuration, we examine a canyon-like structure, i. e. along _a_ the periodicity is shown in Fig. 2b, while along _b_ it continues the structure as it is

depicted. This structure is similar to the suggested pit in refs. 49,50 and investigate how the electronic structure of Sr2RuO4 is affected thereby. The optimized RuO6 rotation angles for

slabs with Sr surface termination (Fig. 2a, left panel) are summarized in Fig. 3 as a function of number of layers _n_ (see also Table S1). We find that the octahedral rotation in both

surface and subsurface show rapid convergence to stable values with the number of layers considered in the slab calculation, indicating the presence of small interlayer couplings, as

expected from resistivity measurements66. Incorporating spin-orbit coupling (SOC) in the structural slab relaxations is not found to play a crucial role for the rotation angles, in contrast

to the role it plays for the electronic properties near the Fermi surface56,59,61 where it was found to be essential. In other words, even though to reproduce the experimental Fermi-surface

shape spin-orbit coupling is essential, it has negligible effect on the structural relaxation which is the central focus of this study. The optimal rotation angle of 7.17∘ at the surface

layer obtained in non-relativistic calculations is in agreement with experiments53,67 and earlier theoretical investigations57,68. Therefore, for the structure optimization we neglect the

effect of SOC in multilayered slabs. Furthermore, we checked that structure optimization using different setups, like surface and subsurface optimization or structural optimization of the

full slab with different depths, leads to changes in the rotation angle of the RuO6 octahedra of at most 0.1∘. We next consider slabs with Ru termination (Fig. 2a, middle panel). In this

case the surface RuO6 octahedra don’t have top apex oxygens and the surface reconstruction after relaxation is less severe. The optimized rotation angles are therefore much smaller than in

the previous case as summarized in Fig. 3 and in Table S2. The slabs exhibit once again a fast convergence in rotation angles with number of layers considered within the slab (see inset of

Fig. 3). We also performed relaxations by considering a 2Sr termination (Fig. 2a, right panel), where the surface is assumed to be terminated at a SrO layer, two layers away from the RuO

plane. In this case we observe, similarly to the Ru termination, a strong suppression of the RuO6 octahedral rotation in the most outer RuO surface (see Fig. 3 and Table S2). The rotation

angles again converge quickly with the number of layers within the slab. As expected from the electronic structure analysis of the effect of RuO6 octahedral rotations in Sr2RuO4 (Fig. 1), we

find bulk-like behavior in the absence of the octahedral rotation for both the 2Sr and Ru terminations. We proceed now with a more complex slab termination. As reported in ref. 49

imperfections in the cleaving process of the crystal, which create small canyon-like structures, enable the observation of a superconducting state in STM. Here, we perform DFT calculations

for one such case, a 2Sr canyon termination (Fig. 2b). For that we choose a trade-off between numerical feasibility and complexity of the structure. The canyon-like structure is built from

previously relaxed Sr-terminated slabs. After removing the atoms in order to resemble the structures suggested in ref. 49, we perform a relaxation of the whole structure. We find that near

the edges of the canyon, a substantial displacement of the atoms occurs - while at the bottom of the pit, the RuO6 octahedral rotation is nearly zero. Figure 4 shows the orbitally resolved

DOS for the 2Sr canyon (Fig. 2b) where the contribution of the surface Ru is shown in shades of dashed blue (Fig. 4a) and the contribution coming from subsurface Ru is shown in shades of

solid red (Fig. 4b). Figure 4c depicts the comparison of the _d__x__y_ orbital projected DOS for the surface and subsurface. By this direct comparison it is visible that the subsurface layer

has a clear bulk-like feature, with a clear peak close to the Fermi level (compare, for instance, with ref. 47, and with Fig. 1c left panel where the electronic structure of bulk Sr2RuO4 is

emulated). As can be seen in Fig. 4 the influence of the RuO6 octahedral rotation is quite drastic - the electronic structure of the subsurface Ru layer retains the position of the bulk

system’s van-Hove singularity while the vHs of the surface Ru is shifted below the Fermi level, again resembling what we observed in the Sr-terminated slab (Fig. 1). This indicates that the

subsurface electronic structure is the same as for bulk Sr2RuO4, since it is not affected by the octahedra rotation. Therefore, bulk-like behavior is expected, i.e. the layer should show

superconductivity when the tip is placed in the area of the canyon, as indicated by STM measurements49,50. DISCUSSION In this work, we investigated via DFT calculations the surface

reconstruction of different charge-neutral surfaces of Sr2RuO4, including experimentally observed canyon structures. Our motivation was to understand the microscopic origin of contradictory

reports of detection of superconductivity in STS/STM measurements of Sr2RuO4. The results of our calculations are condensed into two main quantities which are (i) the structural properties

in terms of the behavior of the RuO6 octahedra at the surface and layers below and (ii) the (partial) density of states of the Ru-d states in the corresponding layers. To examine whether to

expect a structure to have bulk-like behavior, we compare the bulk and relaxed surface electronic structures. From experiments, we know that the bulk system is superconducting1 while clean

SrO-terminated surface samples show no superconductivity45,46,47,48,49. As a probe for whether superconductivity is expected or not, we use the position of the vHs of the band with mainly

_d__x__y_ orbital character relative to the Fermi-level. Experiments under uniaxial strain demonstrated that its position has drastic effects on the critical transition

temperature18,40,63,64,65, both allowing an increase of _T__c_ when approaching the Fermi-level and fueling a rapid suppression once the vHs is pushed below _E__F_. In contrast to the strain

experiments, the movement of the vHs is not the only change induced by the surface reconstruction, i.e. at large octahedral rotation (_θ_ ≥ 6∘) the van-Hove singularity lies below the Fermi

level (_E__F_) and the DOS at _E__F_ is predominantly provided by the new _d__x__y_ pocket opening near the \({\bar{\Gamma}}\) point (see Fig. 1b) right panel), unlike the bulk-like

electronic structure (no RuO6 rotation, Fig. 1b) left panel) where this pocket is absent. We stress that while the property of a single orbital is central in determining _T__c_, the order

parameter is a fully multi-orbital object and the gap on the out-of-plane orbitals is sizable. Thereby we expect that STS/STM can detect the order even though the _d__x__y_-orbital couples

only weakly to the out of plane tunneling. The evolution of the electronic structure under strain was recently reported from ARPES measurements58, where shifts of the surface bands and a

sequence of Lifshitz transitions were detected. We note that our finding of the Lifshitz transition is in line with this observation. The interpretation of the shifts of the surface

electronic structure in terms of bond length changes rather than octahedral rotation58 is a different picture. We note however that application of strain is qualitatively different than

removing a surface layer in a canyon as we simulate in our work, but still could be a potential avenue to expose superconductivity to the surface. We note that the \({\bar{\Gamma}}\) pocket

is slightly higher in energy in ARPES measurements58. This additional feature was however recently argued to be irrelevant for the pairing62 and thereby the suppression of superconductivity

can be understood in rough analogy with the experiments under uniaxial strain. Considering these arguments, it is to be expected that the modifications in the surface electronic structure

also change the tendency towards superconductivity on the surface. As a consequence, searching for a bulk-like electronic structure would potentially enable to observe bulk-like physics. As

a last note, while _T__c_ is mainly influenced by specifics of the _d__x__y_ orbital, the gap is known to be of roughly equal size on all three orbitals from specific heat experiments12,39

which seems at first glance contradictory since the orbitals are only weakly coupled in the kinetic sector. However, as was demonstrated in numerical studies, the interactions in between the

orbitals lead to an enhanced amplitude in all orbitals due to the feedback of one to another19,69. Using this qualitative understanding of how superconductivity is influenced by the

structural state of the Sr2RuO4 and by examining the signatures of the density of states, we can indirectly connect the tendency towards superconducting pairing to the structural state of

the RuO6 octahedra. We find that the density of states in the layers without rotation exhibits similar positions of the van Hove peaks as that of an unreconstructed (bulk) system; in

contrast to layers with significant octahedra rotation, thus connecting the electronic structures in the corresponding layers to the bulk electronic structure. Our calculations corroborate

that for Sr-terminated surfaces, the RuO6 octahedra show a rotation of about 7∘, in agreement with previous investigations53,57,67,68. However, for both the rare 2Sr- and Ru-terminated

surfaces, no significant octahedral rotation angle was found. This suggests that if these latter terminations could be successfully grown or cleaved, superconducting surfaces should be

observed. This in turn would allow for direct measurements of the superconducting order parameter utilizing Bogoliubov quasiparticle interference. Importantly, since the surface electronic

structure in these cases does not essentially deviate from the bulk electronic structure, it is expected that the superconducting order parameter is identical to the bulk as well. In

experiments on these proposed surfaces, it will be crucial to ensure that the observed order parameter indeed matches the bulk one by comparing properties of the surface order to the bulk

order. Natural consistency checks include those between STS spectra/QPI analysis and the nodal positions expected from bulk transport12,16. This suggestion is supported by our 2Sr canyon

slab simulations resembling reported surface imperfections in ref. 49 where we found that the octahedral rotation in the subsurface is essentially absent. Accordingly, the electronic

structure does not differ substantially from bulk - explaining why within these canyons a superconducting gap is observed in STM measurements49,50. Therefore, we argue that STM (or other

surface) experiments do not see the superconducting gap if they are located with their tip on the Sr-terminated surface with a reconstructed surface that contains octahedral rotation. While

so far there has been no report of a clean 2Sr or Ru surface termination, our results suggest that fabricating such a termination could help significantly in determining the gap structure in

Sr2RuO4. Furthermore, this could settle the longstanding debate of whether there is a second order parameter or not16,17,18,36,39,40,70. While a relatively clean surface might be required

to obtain Bogoliubov quasiparticle interference patterns, the observation of a STS/STM gap in canyon defects already allows for a more thorough investigation of the gap structure. METHODS

FIRST PRINCIPLES CALCULATIONS We performed ab initio electronic structure calculations within density functional theory (DFT)71,72 by using the Vienna Ab initio Simulation Package

(VASP)73,74,75 within the pseudo-potential augmented plane-wave76,77 (PAW) basis set. The calculations were performed with the Perdew-Burke-Ernzerhof (PBE)78 exchange correlation functional

as a generalized gradient approximation (GGA), and a plane-wave cutoff of 800 eV was chosen. First the bulk structure was relaxed on a 16 × 16 × 4 _k_-point mesh using the conventional unit

cell of Sr2RuO4. The relaxed unit cell was then transformed to a tetragonal \(\sqrt{2}\times \sqrt{2}\times 1\) unit cell in order to have two inequivalent Ru sites and four inequivalent O

sites in the _a__b_ plane. The convergence criterion was chosen to be 2 ⋅ 10−3 _e__V_/Å for these slabs and 1 ⋅ 10−3 _e__V_/Å for the bulk. From the optimized bulk unit cell we generated

slabs with up to 5 Ru layers with Sr, 2Sr or Ru termination on both ends. A void of 15 Å was set on top of the surfaces. In these slab unit cells we rotated the RuO6 octahedra starting form

their initial position, i. e. 180∘ between two neighboring Ru atoms and the O in between, by adding a displacement DO for the O atoms in the Ru plane dependent on the rotation angle _θ_

$${{\bf{d}}}_{{\rm{O}}}(\theta )=\left(\begin{array}{ccc}0&\tan (\theta )&0\\ -\tan (\theta )&0&0\\ 0&0&0\end{array}\right)\cdot {{\bf{r}}}_{{\rm{O}}},$$ (1) where RO

is the initial positions of the O atoms in the Ru plane. For all slabs we optimized every pair of Ru layers symmetrically. Crosscheck for non symmetric setups were done, however, these had

a higher total energy. The scheme of optimizing was done carefully for all terminations as follows: (i) We first started with one Ru layer. (ii) This was optimized first with a low

resolution energy landscape. (iii) Then we relocated and zoomed in to restart with a higher resolution. (iv) We repeated this procedure until we had a sufficient amount of resolution. (v) As

a last step of refinement we let VASP internally relax, to printout the forces and confirm that we are in a minimum. (vi) Restart with an additional Ru layer, and use the previous optimal

rotation angle as new starting rotation angle. The _k_ mesh for optimizing these structures was 6 × 6 × 1. For the 2Sr canyon structure, we started from the relaxed 3 layer Sr-terminated

slab and expanded the unit cell by \(\sqrt{2}\times \sqrt{2}\times 1\). This supercell was then extended in one direction 3 × 1 × 1. Finally we dug a hole on both surfaces and started a

relaxation. The forces were reduced to 5 ⋅ 10−3_e__V_/Å with a _k_-mesh of 2 × 6 × 1. DATA AVAILABILITY All simulation data is available upon reasonable request. CODE AVAILABILITY

VASP73,74,75 is a commercial program. For plotting the crystal structure vesta79 was used. The Fermi surface cuts were obtained from FermiSurfer80. REFERENCES * Mackenzie, A. P. & Maeno,

Y. The superconductivity of Sr2RuO4 and the physics of spin-triplet pairing. _Rev. Mod. Phys._ 75, 657–712 (2003). Article  ADS  Google Scholar  * Maeno, Y., Kittaka, S., Nomura, T.,

Yonezawa, S. & Ishida, K. Evaluation of spin-triplet superconductivity in Sr2RuO4. _J. Phys. Soc. Jpn._ 81, 011009 (2012). Article  ADS  Google Scholar  * Kallin, C. & Berlinsky, J.

Chiral superconductors. _Rep. Prog. Phys._ 79, 054502 (2016). Article  ADS  Google Scholar  * Mackenzie, A. P., Scaffidi, T., Hicks, C. W. & Maeno, Y. Even odder after twenty-three

years: the superconducting order parameter puzzle of Sr2RuO4. _npj Quantum Mater._ 2, 40 (2017). Article  ADS  Google Scholar  * Ishida, K. et al. Spin-triplet superconductivity in Sr2RuO4

identified by 17o Knight shift. _Nature_ 396, 658–660 (1998). Article  ADS  Google Scholar  * Luke, G. M. et al. Time-reversal symmetry-breaking superconductivity in Sr2RuO4. _Nature_ 394,

558–561 (1998). Article  ADS  Google Scholar  * Xia, J., Maeno, Y., Beyersdorf, P. T., Fejer, M. M. & Kapitulnik, A. High resolution polar Kerr effect measurements of Sr2RuO4: Evidence

for broken time-reversal symmetry in the superconducting state. _Phys. Rev. Lett._ 97, 167002 (2006). Article  ADS  Google Scholar  * Rice, T. M. & Sigrist, M. Sr2RuO4: an electronic

analogue of 3He? _J. Phys.: Condens. Matter_ 7, L643–L648 (1995). ADS  Google Scholar  * Bonalde, I. et al. Temperature dependence of the penetration depth in Sr2RuO4: Evidence for nodes in

the gap function. _Phys. Rev. Lett._ 85, 4775–4778 (2000). Article  ADS  Google Scholar  * NishiZaki, S., Maeno, Y. & Mao, Z. Changes in the superconducting state of Sr2RuO4 under

magnetic fields probed by specific heat. _J. Phys. Soc. Jpn._ 69, 572–578 (2000). Article  ADS  Google Scholar  * Deguchi, K., Mao, Z. Q., Yaguchi, H. & Maeno, Y. Gap structure of the

spin-triplet superconductor Sr2RuO4 determined from the field-orientation dependence of the specific heat. _Phys. Rev. Lett._ 92, 047002 (2004). Article  ADS  Google Scholar  * Hassinger, E.

et al. Vertical line nodes in the superconducting gap structure of Sr2RuO4. _Phys. Rev. X_ 7, 011032 (2017). Google Scholar  * Pustogow, A. et al. Constraints on the superconducting order

parameter in Sr2RuO4 from oxygen-17 nuclear magnetic resonance. _Nature_ 574, 72–75 (2019). Article  ADS  Google Scholar  * Ishida, K., Manago, M., Kinjo, K. & Maeno, Y. Reduction of the

17O Knight Shift in the Superconducting State and the Heat-up Effect by NMR Pulses on Sr2RuO4. _J. Phys. Soc. Jpn._ 89, 034712 (2020). Article  ADS  Google Scholar  * Chronister, A. et al.

Evidence for even parity unconventional superconductivity in Sr2RuO4. _Proc. Natl Acad. Sci._ 118, e2025313118 (2021). Article  Google Scholar  * Benhabib, S. et al. Ultrasound evidence for

a two-component superconducting order parameter in Sr2RuO4. _Nat. Phys._ 17, 194–198 (2021). Article  Google Scholar  * Ghosh, S. et al. Thermodynamic evidence for a two-component

superconducting order parameter in Sr2RuO4. _Nat. Phys._ 17, 199–204 (2021). Article  Google Scholar  * Grinenko, V. et al. Split superconducting and time-reversal symmetry-breaking

transitions in Sr2RuO4 under stress. _Nat. Phys._ 17, 748–754 (2021). Article  Google Scholar  * Rømer, A. T., Scherer, D. D., Eremin, I. M., Hirschfeld, P. J. & Andersen, B. M. Knight

shift and leading superconducting instability from spin fluctuations in Sr2RuO4. _Phys. Rev. Lett._ 123, 247001 (2019). Article  ADS  Google Scholar  * Røising, H. S., Scaffidi, T., Flicker,

F., Lange, G. F. & Simon, S. H. Superconducting order of Sr2RuO4 from a three-dimensional microscopic model. _Phys. Rev. Res._ 1, 033108 (2019). Article  Google Scholar  * Gingras, O.,

Nourafkan, R., Tremblay, A.-M. S. & Côté, M. Superconducting symmetries of Sr2RuO4 from first-principles electronic structure. _Phys. Rev. Lett._ 123, 217005 (2019). Article  ADS  Google

Scholar  * Suh, H. G. et al. Stabilizing even-parity chiral superconductivity in Sr2RuO4. _Phys. Rev. Res._ 2, 032023 (2020). Article  Google Scholar  * Kaba, S.-O. & Sénéchal, D.

Group-theoretical classification of superconducting states of strontium ruthenate. _Phys. Rev. B_ 100, 214507 (2019). Article  ADS  Google Scholar  * Ramires, A. & Sigrist, M.

Superconducting order parameter of Sr2RuO4: A microscopic perspective. _Phys. Rev. B_ 100, 104501 (2019). Article  ADS  Google Scholar  * Acharya, S. et al. Evening out the spin and charge

parity to increase T_c_ in Sr2RuO4. _Commun. Phys._ 2, 163 (2019). Article  Google Scholar  * Wang, Z., Wang, X. & Kallin, C. Spin-orbit coupling and spin-triplet pairing symmetry in

Sr2RuO4. _Phys. Rev. B_ 101, 064507 (2020). Article  ADS  Google Scholar  * Rømer, A. T. et al. Theory of strain-induced magnetic order and splitting of T_c_ and Ttrsb in Sr2RuO4. _Phys.

Rev. B_ 102 (2020). * Rømer, A. T. & Andersen, B. M. Fluctuation-driven superconductivity in Sr2RuO4 from weak repulsive interactions. _Mod. Phys. Lett. B_ 34, 2040052 (2020). Article 

ADS  Google Scholar  * Rømer, A. T., Hirschfeld, P. J. & Andersen, B. M. Superconducting state of Sr2RuO4 in the presence of longer-range Coulomb interactions. _Phys. Rev. B_ 104, 064507

(2021). Article  ADS  Google Scholar  * Kivelson, S. A., Yuan, A. C., Ramshaw, B. & Thomale, R. A proposal for reconciling diverse experiments on the superconducting state in Sr2RuO4.

_npj Quantum Mater._ 5, 43 (2020). Article  ADS  Google Scholar  * Clepkens, J., Lindquist, A. W. & Kee, H.-Y. Shadowed triplet pairings in Hund’s metals with spin-orbit coupling. _Phys.

Rev. Res._ 3, 013001 (2021). Article  Google Scholar  * Willa, R., Hecker, M., Fernandes, R. M. & Schmalian, J. Inhomogeneous time-reversal symmetry breaking in Sr2RuO4. _Phys. Rev. B_

104, 024511 (2021). Article  ADS  Google Scholar  * Rømer, A. T., Maier, T. A., Kreisel, A., Hirschfeld, P. J. & Andersen, B. M. Leading superconducting instabilities in

three-dimensional models for Sr2RuO4. _Phys. Rev. Res._ 4, 033011 (2022). Article  Google Scholar  * Roig, M., Rømer, A. T., Kreisel, A., Hirschfeld, P. J. & Andersen, B. M.

Superconductivity in multiorbital systems with repulsive interactions: Hund’s pairing versus spin-fluctuation pairing. _Phys. Rev. B_ 106, L100501 (2022). Article  ADS  Google Scholar  *

Røising, H. S., Wagner, G., Roig, M., Rømer, A. T. & Andersen, B. M. Heat capacity double transitions in time-reversal symmetry broken superconductors. _Phys. Rev. B_ 106, 174518 (2022).

Article  ADS  Google Scholar  * Palle, G. et al. Constraints on the superconducting state of Sr2RuO4 from elastocaloric measurements. _Phys. Rev. B_ 108, 094516 (2023). Article  ADS  Google

Scholar  * Profe, J. B., Beck, S., Kennes, D. M., Georges, A. & Gingras, O. Competition between d-wave superconductivity and magnetism in uniaxially strained Sr2RuO4. _npj Quantum

Mater._ 9, 53 (2024). Article  Google Scholar  * Andersen, B. M., Kreisel, A. & Hirschfeld, P. J. Spontaneous time-reversal symmetry breaking by disorder in superconductors. _Front.

Phys._ 12, 1353425 (2024). Article  Google Scholar  * Li, Y.-S. et al. High-sensitivity heat-capacity measurements on Sr2RuO4 under uniaxial pressure. _Proc. Natl Acad. Sci._ 118,

e2020492118 (2021). Article  Google Scholar  * Li, Y.-S. et al. Elastocaloric determination of the phase diagram of Sr2RuO4. _Nature_ 607, 276–280 (2022). Article  ADS  Google Scholar  *

Firmo, I. A. et al. Evidence from tunneling spectroscopy for a quasi-one-dimensional origin of superconductivity in Sr2RuO4. _Phys. Rev. B_ 88, 134521 (2013). Article  ADS  Google Scholar  *

Sharma, R. et al. Momentum-resolved superconducting energy gaps of Sr2RuO4 from quasiparticle interference imaging. _Proc. Natl Acad. Sci._ 117, 5222–5227 (2020). Article  ADS  Google

Scholar  * Bhattacharyya, S. et al. Superconducting gap symmetry from Bogoliubov quasiparticle interference analysis on Sr2RuO4. _Phys. Rev. B_ 107, 144505 (2023). Article  ADS  Google

Scholar  * Suderow, H. et al. A nodeless superconducting gap in Sr2RuO4 from tunneling spectroscopy. _N. J. Phys._ 11, 093004 (2009). Article  Google Scholar  * Kambara, H. et al. Scanning

Tunneling Microscopy and Spectroscopy of Sr2RuO4. In _AIP Conference Proceedings_, vol. 850, 539–540 (AIP, 2006). * Lupien, C., Dutta, S. K., Barker, B. I., Maeno, Y. & Davis, J. C.

mK-STM studies of the temperature- and field-dependence of the quasiparticle spectrum of Sr2RuO4. _Phys. C. Supercond._ 471, 708–710 (2011). Google Scholar  * Marques, C. A. et al.

Magnetic-field tunable intertwined checkerboard charge order and nematicity in the surface layer of Sr2RuO4. _Adv. Mater._ 33, 2100593 (2021). Article  Google Scholar  * V. Madhavan, private

communication. * Olivares Rodriguez, J. Stress and crystal imperfections: Tools for the exploration of unconventional superconductivity via scanning tunneling microscopy, U. Illinois Ph.D.

thesis (2022). * De Almeida Marques, C. Imaging emergent correlated phases in the strontium ruthenates, University of St Andrews Ph.D. thesis (2022). * Mueller, E. et al. Superconducting

penetration depth through a van Hove singularity: Sr2RuO4 under uniaxial stress. _Phys. Rev. B_ 110, L100502 (2024). * Nakatsuji, S. & Maeno, Y. Quasi-two-dimensional Mott transition

system Ca2−_x_Sr_x_RuO4. _Phys. Rev. Lett._ 84, 2666–2669 (2000). Article  ADS  Google Scholar  * Matzdorf, R., Kimura, T., Tokura, Y. & Plummer, E. W. Surface structural analysis of the

layered perovskite Sr2RuO4 by LEED _I_(_V_). _Phys. Rev. B_ 65, 085404 (2002). Article  ADS  Google Scholar  * Pennec, Y. et al. Cleaving-temperature dependence of layered-oxide surfaces.

_Phys. Rev. Lett._ 101, 216103 (2008). Article  ADS  Google Scholar  * Kreisel, A. et al. Quasi-particle interference of the van hove singularity in Sr2RuO4. _npj Quantum Mater._ 6, 100

(2021). Article  ADS  Google Scholar  * Tamai, A. et al. High-Resolution Photoemission on Sr2RuO4 Reveals Correlation-Enhanced Effective Spin-Orbit Coupling and Dominantly Local

Self-Energies. _Phys. Rev. X_ 9, 021048 (2019). Google Scholar  * Chandrasekaran, A. et al. Engineering higher order Van Hove singularities in two dimensions: the example of the surface

layer of Sr2RuO4 (2023). ArXiv:2310.15331 [cond-mat]. * Abarca Morales, E. et al. Hierarchy of Lifshitz transitions in the surface electronic structure of Sr2RuO4 under uniaxial compression.

_Phys. Rev. Lett._ 130, 096401 (2023). Article  ADS  Google Scholar  * Veenstra, C. N. et al. Spin-orbital entanglement and the breakdown of singlets and triplets in Sr2RuO4 revealed by

spin- and angle-resolved photoemission spectroscopy. _Phys. Rev. Lett._ 112, 127002 (2014). Article  ADS  Google Scholar  * Damascelli, A. et al. Fermi surface, surface states, and surface

reconstruction in Sr2RuO4. _Phys. Rev. Lett._ 85, 5194–5197 (2000). Article  ADS  Google Scholar  * Haverkort, M. W., Elfimov, I. S., Tjeng, L. H., Sawatzky, G. A. & Damascelli, A.

Strong spin-orbit coupling effects on the Fermi surface of Sr2RuO4 and Sr2RhO4. _Phys. Rev. Lett._ 101, 026406 (2008). Article  ADS  Google Scholar  * Profe, J. B. et al. The magic angle of

Sr2RuO4: optimizing correlation-driven superconductivity. arXiv preprint https://arxiv.org/abs/2405.14926 (2024). * Steppke, A. et al. Strong peak in T_c_ of Sr2RuO4 under uniaxial pressure.

_Science_ 355, (2017). * Watson, C. A., Gibbs, A. S., Mackenzie, A. P., Hicks, C. W. & Moler, K. A. Micron-scale measurements of low anisotropic strain response of local _T__c_ in

Sr2RuO4. _Phys. Rev. B_ 98, 094521 (2018). Article  ADS  Google Scholar  * Jerzembeck, F. et al. The superconductivity of Sr2RuO4 under c-axis uniaxial stress. _Nat. Commun._ 13, 4596

(2022). Article  ADS  Google Scholar  * Hussey, N. E. et al. Normal-state magnetoresistance of Sr2RuO4. _Phys. Rev. B_ 57, 5505–5511 (1998). Article  ADS  Google Scholar  * Matzdorf, R. et

al. Ferromagnetism stabilized by lattice distortion at the surface of the p-wave superconductor Sr2RuO4. _Science_ 289, 746–748 (2000). Article  ADS  Google Scholar  * Veenstra, C. N. et al.

Determining the Surface-To-Bulk Progression in the Normal-State Electronic Structure of Sr2RuO4 by Angle-Resolved Photoemission and Density Functional Theory. _Phys. Rev. Lett._ 110, 097004

(2013). Article  ADS  Google Scholar  * Strand, H. U. R., Zingl, M., Wentzell, N., Parcollet, O. & Georges, A. Magnetic response of Sr2RuO4: Quasi-local spin fluctuations due to Hund’s

coupling. _Phys. Rev. B_ 100, 125120 (2019). Article  ADS  Google Scholar  * Mueller, E. et al. Constraints on a split superconducting transition under uniaxial strain in Sr2RuO4 from

scanning squid microscopy. _Phys. Rev. B_ 108, 144501 (2023). Article  ADS  Google Scholar  * Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. _Phys. Rev._ 136, B864–B871 (1964).

Article  ADS  MathSciNet  Google Scholar  * Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. _Phys. Rev._ 140, A1133–A1138 (1965). Article 

ADS  MathSciNet  Google Scholar  * Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. _Phys. Rev. B_ 47, 558–561 (1993). Article  ADS  Google Scholar  * Kresse, G.

& Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. _Phys. Rev. B_ 54, 11169–11186 (1996). Article  ADS  Google Scholar  *

Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. _Computational Mater. Sci._ 6, 15–50 (1996).

Article  Google Scholar  * Blöchl, P. E. Projector augmented-wave method. _Phys. Rev. B_ 50, 17953–17979 (1994). Article  ADS  Google Scholar  * Kresse, G. & Joubert, D. From ultrasoft

pseudopotentials to the projector augmented-wave method. _Phys. Rev. B_ 59, 1758–1775 (1999). Article  ADS  Google Scholar  * Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized

gradient approximation made simple. _Phys. Rev. Lett._ 77, 3865–3868 (1996). Article  ADS  Google Scholar  * Momma, K. & Izumi, F. _V_ESTA3 for three-dimensional visualization of

crystal, volumetric and morphology data. _J. Appl. Crystallogr._ 44, 1272–1276 (2011). * Kawamura, M. Fermisurfer: Fermi-surface viewer providing multiple representation schemes. _Computer

Phys. Commun._ 239, 197–203 (2019). Article  ADS  Google Scholar  Download references ACKNOWLEDGEMENTS The authors are grateful to S. Mukherjee for valuable discussions in the early stages

of this project and H. Suderow and V. Madhavan for providing valuable information concerning STM measurements of Sr2RuO4. R.V., J.B.P. and A.V. gratefully acknowledge support by the Deutsche

Forschungsgemeinschaft (DFG, German Research Foundation) for funding through Project No. 411289067 (VA117/15-1) and TRR 288 — 422213477 (project A05). A.K. acknowledges support by the

Danish National Committee for Research Infrastructure (NUFI) through the ESS-Lighthouse Q-MAT. P.J.H. acknowledges support from NSF-DMR-2231821. FUNDING Open Access funding enabled and

organized by Projekt DEAL. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Institut für Theoretische Physik, Goethe-Universität, 60438, Frankfurt am Main, Germany Adrian Valadkhani, Jonas B.

Profe & Roser Valentí * Niels Bohr Institute, University of Copenhagen, DK-2200, Copenhagen, Denmark Andreas Kreisel * Department of Physics, University of Florida, Gainesville, FL,

32611, USA P. J. Hirschfeld Authors * Adrian Valadkhani View author publications You can also search for this author inPubMed Google Scholar * Jonas B. Profe View author publications You can

also search for this author inPubMed Google Scholar * Andreas Kreisel View author publications You can also search for this author inPubMed Google Scholar * P. J. Hirschfeld View author

publications You can also search for this author inPubMed Google Scholar * Roser Valentí View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS

A.V. performed the DFT simulations. A.V., J.B.P., A.K., P.J.H. and R.V. contributed to the data analysis, discussions and writing of the manuscript. CORRESPONDING AUTHORS Correspondence to

Adrian Valadkhani or Roser Valentí. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains

neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION RIGHTS AND PERMISSIONS OPEN ACCESS This

article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as

you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party

material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s

Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.

To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Valadkhani, A., Profe, J.B., Kreisel, A. _et

al._ Why scanning tunneling spectroscopy of Sr2RuO4 sometimes doesn’t see the superconducting gap. _npj Quantum Mater._ 9, 78 (2024). https://doi.org/10.1038/s41535-024-00687-7 Download

citation * Received: 28 May 2024 * Accepted: 14 September 2024 * Published: 13 October 2024 * DOI: https://doi.org/10.1038/s41535-024-00687-7 SHARE THIS ARTICLE Anyone you share the

following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer

Nature SharedIt content-sharing initiative