Distortion-stabilized ordered structures in a2bb’o7 mixed pyrochlores

ABSTRACT Pyrochlore oxides (A2B2O7) are interesting for a number of technological applications, including radiation damage tolerance and as ionic conductors. Mixed pyrochlores—containing two

A and/or two B site cations—provide even more flexibility for tailoring properties owing to the diverse chemical and configurational degrees of freedom accessible within this chemical

space. Here, we examine relative stability of different cation orderings in one model double pyrochlore Gd2(Zr_x_Ti1−_x_)2O7, as a function of Zr content _x_. Our results show that, in the

presence of some very specific local cation arrangements, certain cation-ordered compositions in this system are highly stabilized as a result of large oxygen relaxation displacements,

leading to the formation of an ordered ‘double’ pyrochlore structure. The origins of these anomalous oxygen relaxations are traced back to both the local cation symmetry and a strong

chemical preference of Zr atoms towards adopting a 7-fold coordination environment, as opposed to a 6-fold coordination available in a regular pyrochlore structure. Subsequently, we examine

the stability of this type of ordering in 131 other pyrochlore compositions. Implications of our findings are discussed in relation to the observed composition-dependent ionic conductivity

in these systems and connections with previously reported experimental findings are made. SIMILAR CONTENT BEING VIEWED BY OTHERS A COMPREHENSIVE EXAMINATION OF THE LOCAL- AND LONG-RANGE

STRUCTURE OF SB6O13 PYROCHLORE OXIDE Article Open access 12 October 2020 ANTIFERROELECTRICITY IN A FAMILY OF PYROXENE-LIKE OXIDES WITH RICH POLYMORPHISM Article Open access 03 August 2020

DYNAMICAL GROUND STATE IN THE XY PYROCHLORE YB2GASBO7 Article Open access 05 May 2021 INTRODUCTION Oxides are an attractive class of materials due to their extreme variety in functionality.

This richness arises from the very flexible chemistry of these materials. Indeed, beyond base compounds such as binaries and ternaries, the possibilities for modifying the chemistry of most

oxides is nearly limitless. Such multicomponent oxides often have significantly improved performance over the end-member compounds, with enhanced scintillation,1 ferroelectricity,2,3

piezoelectricity,4 high temperature stability5 and catalytic response.6 By expanding the chemical space in which compound discovery can occur by considering mixed oxides, the potential for

materials discovery expands exponentially. Thus, in the quest for new materials, understanding the structures that result from mixing simpler compounds to form more complex materials is

critical. This has been extensively studied in some cases. For example, in the perovskite family of compounds (ABO3), the properties of so-called double perovskites have been examined by

multiple groups.7,8 These compounds, containing two A and/or two B cations, can form ordered structures for some chemistries9,10,11 and these orderings are known to modify functional

properties, including oxygen transport12,13 and ferromagnetism.14 In the case of pyrochlores (A2B2O7), the subject of the current work, mixed systems have been used to understand, amongst

other properties, the role of disorder in both radiation damage tolerance and ionic conductivity. Simply, as, for example, the B cation is gradually changed from Ti and Zr, the propensity

for cation disorder increases and this has been correlated to the functionality of the material. In materials such as Gd2(Zr_x_Ti1−_x_)2O7 (GZTO), as the chemistry shifts from _x_ = 0 to _x_

 = 1, disorder increases and so does the resistance to amorphization15,16,17 and the magnitude of ionic conductivity.18 Thus, in many studies of ionic conductivity, disorder is induced in

the system via the introduction of additional cations.18,19,20 These studies have led to conflicting results, with some showing a direct increase in the conductivity vs. disorder18 while

others suggest that the ordered phase has a higher conductivity than the disordered state.19,20 Implicitly, these studies assume a smooth and gradual transition from the ordered state to the

disordered state with changes in chemistry. However, this is not always the case. For example, NMR studies show that, depending on both the A and B chemistry of the compound, mixed

pyrochlores can form either solid solutions or phase separate.21,22 This complicates the establishment of structure-property relationships with disorder. In this work, we consider a further

complication, the possibility that, even in cases where the cations form a solid solution in mixed pyrochlores, they may form ordered structures, reminiscent of the double perovskites,

rather than a disordered solid solution. These ordered structures would naturally exhibit different transport behavior than a random solid solution, as we have seen previously for double

perovskites.13 Thus, in any campaign to establish structure-property relationships for mixed pyrochlores, one must have a solid understanding of what the detailed atomic structure of the

mixed pyrochlore is. We use density functional theory (DFT) to investigate the possible orderings as a function of _x_ in Gd2(Zr_x_Ti1−_x_)2O7. We identify unique ordered ground states that

are stabilized by significant distortions in the oxygen sublattice, distortions that increase the coordination of Zr from 6 to 7. We then examine the stability of this ordering in other

pyrochlore compositions. We find that in many compositions in which the A cation is of sufficient size and the B sublattice contains sufficient Zr and/or Hf, ordered structures are

thermodynamically preferred, at least at low temperature. These results offer new insight into the structures that drive performance in mixed pyrochlores. RESULTS The DFT-computed mixing

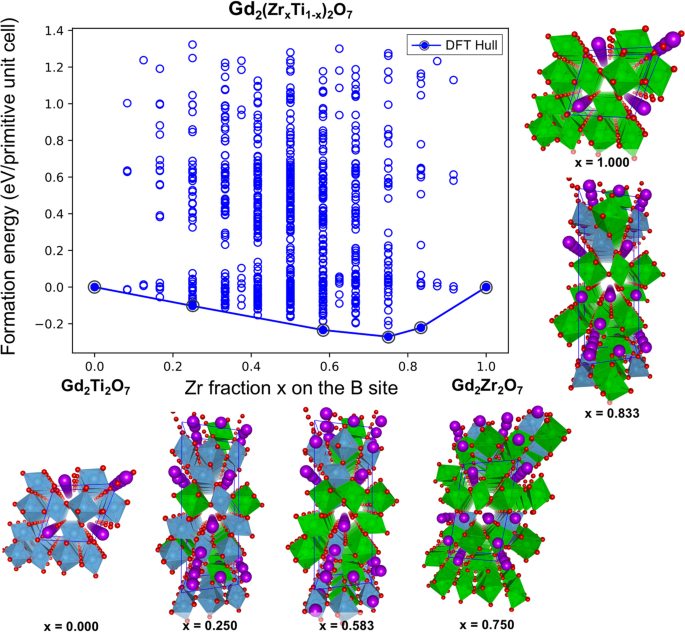
energies (_i_._e_., the formation energies with respect to the pure pyrochlore chemistries with _x_ = 0 and _x_ = 1) for the entire set of 704 configurations enumerated within the

generalized Gd2(Zr_x_Ti1−_x_)2O7 formula unit are presented in Fig. 1. In addition to the end points, the DFT-computed convex hull identifies four different ground-state structures with

compositions x = 0.25, 0.583, 0.75 and 0.833 (the relaxed geometries are provided in the Supporting Information). The atomistic structures for the identified ground-state ordered structures

are also depicted in Fig. 1. The DFT results in Fig. 1 indicate that, as the composition varies from Ti rich to Zr rich, there are ordered structures of Ti and Zr on the B-sublattice that

are thermodynamically stable. Thus, similar to double perovskites, these mixed pyrochlore systems may also exhibit some tendency to form ordered solid solutions. Further, the propensity for

ordering is greatest for a Zr-rich composition of _x_ = 0.75, indicating that the propensity for forming an ordered structure is sensitive to the composition of the mixed system. We further

note that the specific orderings identified in Fig. 1 between _x_ = 0 and _x_ = 1 (_i_._e_., mixed pyrochlores) all have a superstructure that is longer-ranged than simple “single”

pyrochlore structure. In other words, the orderings are not possible with the standard pyrochlore primitive unit cell containing 22 atoms (i.e., two formula units) and need either 44-atom

(for _x_ = 0.75) or 66-atom supercells (for _x_ = 0.25, 0.583, and 0.833). To look for specific signatures for the aforementioned cation ordering, in Fig. 2 we compare the X-ray diffraction

(XRD) patterns for mixed GZTO (using the DFT-computed ground-state structure with _x_ = 0.75 that exhibits the lowest mixing energy) and GZO pyrochlores. It can be seen that as a consequence

of B-site ordering some of the peaks in the “single” pyrochlore GZO are split in the mixed GZTO structure. Furthermore, we also find some new (weak) peaks at various angles that are a

reflection of the ordering in the mixed structure. The DFT calculations provide the zero-Kelvin ground-state structure and a range of higher-energy metastable structures for each

composition. Thus, while the ground states are ordered structures, it is possible that their range of stability versus temperature is rather limited. One approach to understand the

temperature-dependent phase stability of these structures is to use Monte Carlo. Given the expense of doing Monte Carlo directly with DFT energetics, we turn to CE to parameterize an

effective Hamiltonian. As a next step, we use the DFT computations to fit a CE Hamiltonian to describe energetics of any given atomic configuration and composition _x_ for the B-site ordered

pyrochlore chemistries. We included the entire set of 704 configurations in the CE fitting while closely following the approach previously described.23 During the effective cluster

interactions (ECI) optimization procedure, we systematically considered clusters with up to _n_-body interactions with _n_ ∈ [4, 7] while gradually varying the maximum allowed site spacing

between the _n_-body clusters from 7 Å to 10 Å. Our CE analysis showed that while CE fits with small and moderate basis sets failed to describe the DFT grounds states, ECIs chosen from a

much larger set (with up to 7-body interactions and maximum allowed site spacing of 10 Å) were able to adequately capture the relative energetics of the structures in the CE training set

(see Fig. S1 in the Supporting Information). Although the adopted ECI optimization procedure explicitly included a _k_-fold cross-validation strategy to select the best set of ECIs (in order

to avoid overfitting to the training data and thereby leading to a better generalizability on unseen configurations), we found that the unusually large basis sets that were eventually able

to provide a good fit for the entire set of low-energy DFT configurations inevitably led to an overfitting of the training data. To further understand the poor performance of the CE fits to

the DFT-computed energetics, we looked into basis and lattice relaxation patterns of the DFT configurations used in the fitting procedure. Our analysis identifies large basis deformations

for a subset of the compounds as a cause of this problem. More specifically, we find that in certain local chemical environments O atoms display unusually large relaxation displacements

(~1.5 Å), which not only lower the energies and volumes of the supercells significantly, but also result in local coordination environment changes of the nearby cations. Essentially, a

subset of oxygen atoms displace away from their initial pyrochlore lattice positions, forming a structure that does not correspond exactly to that of pyrochlore. Such relaxations have not

been previously reported for any pyrochlore chemistries, to the best of our knowledge. In order to quantify the extent of the basis deformations resulting from the anomalous O relaxations,

we define a cost function that describes the degree to which basis sites have relaxed with respect to the ideal pyrochlore structure. The basis deformation cost function is defined as the

mean squared displacement of atoms from their position in the relaxed ideal structure (i.e., a reference structure accounting for the lattice relaxations but the internal coordinates fixed

to the unrelaxed ideal positions). Figure 3a, b present formation energies and volumes of the relaxed structures per 22 atom primitive cell as a function of composition, with the marker

colors representing the extent of the basis deformation. It is interesting to note that while ground-state compounds with _x_ < 0.5 (i.e., the Ti-rich chemistries) exhibit only minimal

relaxations with respect to the ideal pyrochlore configuration, the ground states with Zr-rich chemistries consistently show a significant amount of basis deformation. Furthermore, these

local relaxations also result in a lowering of the overall volume of the supercells. This can be seen from Fig. 3b, where mixing of the two pyrochlore chemistries, in general, leads to

configurations that show either equal or larger volumes with respect to what is expected from a simple linear interpolation, but those configurations showing relatively large basis

deformations clearly stand out with significantly lower supercell volumes. To illustrate the nature of the local O relaxations, we take the specific example of the _x_ = 0.75 ground-state

configuration. Figure 3c, d present the unrelaxed and DFT-relaxed supercell geometries, respectively, for this ground-state structure. The relaxation amplitudes and directions of the O atoms

that are largely responsible for the large basis deformation are identified with black arrows in Fig. 3c. It can be seen that as a result of the relaxation, O atoms common to the two Ti

octahedra move significantly closer to a nearby Zr octahedron. As a result, the coordination environment of the Zr atom changes from 6-fold to 7-fold, while the two Ti atoms remain 6-fold

coordinated, albeit with slightly distorted octahedra, as shown in Fig. 3e. Our analysis shows that as a general requirement for the aforementioned large O relaxations to occur, the

following two conditions have to be met: (1) an O atom must be common to the two corner sharing Ti octahedra and (2) a nearby Zr atom must have an asymmetric local atomic environment of

surrounding cations. As an example, to illustrate the second condition, Fig. 3f–g depict two representative cases from our DFT-computed dataset where the first condition is met for both

structures, however, owing to the local symmetry breaking, only the Zr atoms in the supercell shown in Fig. 3g can relax to a 7-fold coordinated environment. Note that the symmetry argument

made above also explains why the pure _x_ = 1 case (i.e., the Gd2Zr2O7 single pyrochlore) does not exhibit such O distortions, although Zr atoms favor a 7-fold coordination. To further

understand the O relaxations in the context of well established notions of the “kagome” pattern formed by oxygen in single pyrochlores,24,25 we take a look at the collective patterns of

atoms in a oxygen–metal–oxygen layer stacking normal to the [111] direction corresponding to a pseudo-cubic pyrochlore supercell, as shown in Fig. 4a. We note here that the pyrochlore (with

stoichiometry M4O7, without differentiating the two different metal ions M) structure is fundamentally related to a parent fluorite (MO2) structure. Owing to the different metal–oxygen

stoichiometry, however, the individual structure of oxygen atoms in each layer in the two structures differs. More specifically, pyrochlore differs from fluorite in that half of the oxygen

planes contain structural vacancies that form a “kagome” pattern and have the extra complexity of having two different cationic species. In Fig. 4, we compare the local O relaxation patterns

in relaxed Gd2(Zr0.75Ti0.25)2O7 (Fig. 4d, e) with the corresponding bulk-like single pyrochlore structure (Fig. 4b, c). For easy comparison, we show three stacked oxygen–metal–oxygen layers

(side view shown in Fig. 4a and also identified in the central panel) where the central metal layer contains only Gd and Ti cations and the oxygen layer directly above the metal layer

contains O atoms that exhibit the predicted anomalous relaxations. While oxygen atoms in both the top and the bottom layers are visible in Fig. 4b, d, only top layer oxygen atoms are shown

in Fig. 4c, e, and the “kagome” pattern formed by oxygen atoms in the top layer is highlighted in selected panels as a guide to the eye. From Fig. 4a–e, it can be seen that as a result of

the O relaxations of selected O atoms in the top layer (identified by black arrows in the right panels) alternate triangles in the “kagome” pattern” are affected as the O atoms relax from

the vertices to the near-centroid positions. A physically meaningful CE fit can still be possible in the presence of a limited set of training configurations that lead to large basis

deformations upon relaxation, provided the resulting structures are sufficiently higher in energy with respect to the ground-state structures and therefore minimally contribute to the

determination of lower regions of the potential energy surfaces. In such a situation, omitting these structures from the training dataset used in the CE fitting generally improves the

quality of the resulting fits, without sacrificing the underlying “physics” of the problem. However, in the present case, a large fraction of the identified ground-state chemistries (i.e.,

all the mixed Zr-rich cases) exhibit large basis deformations and therefore an effective Hamiltonian obtained by refitting a CE model after removing the structures that exhibit anomalously

large O relaxations will not be a very realistic one. The inability to fit a CE Hamiltonian for the Gd2(Zr_x_Ti1−_x_)2O7 mixed pyrochlore system within the scope of this work prevents us

from examining the thermal phase diagram and determining the stability field for the ordered structures. While this is a negative result, our DFT-based results clearly show that certain

ordered mixed pyrochlore chemistries are indeed thermodynamically favorable—with a strong theoretical evidence that the local chemical environments in such mixed or _double_ pyrochlores may

significantly deviate from their _single_ pyrochlore bulk counterparts. The results presented thus far naturally lead to the following question: “How general are these findings?” To address

this question as to whether the theoretical findings are specific to the Gd2(Zr_x_Ti1−_x_)2O7 mixed pyrochlore system or represent the behavior of a much wider class of chemistries, we next

explore chemical trends within a set of 132 different mixed pyrochlore chemistries of A2(B0.25B'0.75)2O7-type. The details of the specific choices considered for A, B and B’ chemistries

are provided in the Methods section, towards the end of the manuscript. An analysis identical to that for Gd2(Zr_x_Ti1−_x_)2O7 across this entire chemical space would require

DFT-computations of 704 compounds for each of these chemistries—beyond the scope of the present study. Therefore, the mixed pyrochlores are simulated using the supercell configuration that

exhibits the lowest mixing enthalpies for the Gd2(Zr_x_Ti1−_x_)2O7 system. We note that the specific ordering we have chosen to study relative trends across different chemistries may not

represent ground-state configurations for the respective chemistries, but mixing energies computed with this ordering certainly constitute an upper bound on the minimum energy of mixing for

the corresponding A2(B0.25B'0.75)2O7-type double pyrochlores. More importantly, using this structure and the associated cation ordering for the target chemical space exploration allows

for O relaxations that are responsible for Zr coordination switching from a 6-fold to a 7-fold environment upon relaxation in Gd2(Zr0.75Ti0.25)2O7 with a large energetic contribution to the

mixing energy. Thus, this also allows us to gain further insight into the chemical driver of the large O relaxation. Figure 5a presents results of our DFT-computed mixing energies for the

aforementioned 132 A2(B0.25B'0.75)2O7 double pyrochlores. The chemistries are grouped according to the A-site chemistries in different panels, which are presented in decreasing order of

the A elemental empirical radii going from A = La to A = Lu.26 For a given A-site chemistry, B and B' chemistries are identified along the vertical and horizontal axis, respectively.

Several interesting observations can be made from the results presented in Fig. 5a. Most remarkably, the mixing energy patterns in different panels can be visually classified in to two

different classes. The chemistries with A ∈{La, Pr, Nd, Sm} appear to behave qualitatively different from the rest. A deeper case-by-case analysis reveals that within this set of compounds

the aforementioned O relaxation displacements are not energetically favorable, irrespective of the B and B’ chemistries. In contrast, for the double pyrochlore chemistries with A ∈{Y, Gd,

Tb, Dy, Ho, Er, Lu}, a number of B and B' chemistries exhibit the energetically favorable mixing driven largely by the O relaxation displacements, similar to those identified in Fig. 3

for Gd2(Ti0.25Zr0.75)2O7. In particular, the double pyrochlore chemistries with Zr and Hf atoms at the B’ site generally show both favorable mixing tendencies as well as the anomalous O

relaxation displacements. To further establish the fact that the chemical trends in mixing energies within this subset of compounds are indeed largely dictated by the O relaxation

displacements, in Fig. 5b we present the energy contributions due to O relaxation displacements to the total mixing energies (_cf_. Fig. S2 in the Supporting Information for the associated

supercell volume changes). In each case, the relaxation energies are computed by comparing the energetics of a completely relaxed structure with the one where all internal coordinates are

allowed to relax except the O atom that exhibits anomalous relaxation displacement (_cf_. Fig. 3e). This is practically carried out by restricting the relaxation displacements of the O atom

as well as the nearby B’ site atom whose coordination is altered after the relaxation (note that just restricting the relaxation of the O atoms internal coordinates would not be sufficient,

as the rest of the supercell atoms can then relax relative to the O atom). Figure 5b clearly demonstrates that the mixing energy trends in this set of compounds are indeed largely governed

by the relaxation displacements of the O atom. That is, the most stable of the mixed compounds in Fig. 5a correspond to those in which allowing the O relaxation to occur results in the

biggest lowering of energy in Fig. 5b. Most interestingly, Fig. 5a points to other compositions in which the propensity of ordering of the mixed phases might be even higher than in

Gd2(Zr_x_Ti1−_x_)2O7. For example within the A = Gd system, a composition of 75% Zr and 25% Hf exhibits significantly stronger ordering tendencies. There are also strongly ordered pairings

in the A = Ho, Er, and La families of compounds, many involving mixings of Zr and Hf, but some combinations with Ti and even Sn are relatively stable. Thus, in experimental searches for

ordered mixed pyrochlores, some of these compositions may prove more fruitful. Conversely, compounds involving mixing Sn and Ti on the B sublattice are almost universally unfavorable, at

least with the ordered structure used here. There have been multiple studies, several using NMR, to examine mixed pyrochlores containing Sn. In the case of Sn and Ti pairings, if the A

cation was Y, the system formed a solid solution21 while, when A = La, the system tended to phase separate or even from a perovskite phase.22 Our results are not directly comparable to these

experiments as our calculations are at 0 K and we are unable, because of the lack of a suitable CE, to examine the finite temperature behavior of the mixed systems. That said, Fig. 5a

indicates that Ti/Sn pairings in the A = Y pyrochlore family do not want to adopt the ordered structure found for GZTO. Thus, the fact that it wants to form a solid solution suggests that

other ordered structures might be favorable. On the other hand, electron diffraction and NMR studies of Sn/Zr pairings in A = Y pyrochlores reveal that there is evidence of a longer-ranged

ordering than that of pyrochlore.27 While those authors were not able to identify the nature of the ordering, our results suggest that this system, at least in the Zr-rich case, would tend

to form an ordered structure at low temperature. As always, there is the possibility that another even more stable structure exists for this compound as well. We also note that the double

pyrochlore mixing energies for this set of compounds sensitively depend on the nature of the B’ cations (for a given A site chemistry) and the underlying chemical trends can easily be

rationalized in terms of relative size and chemical bonding tendencies of the B’ elements. While Ti and Sn cations exhibit relatively smaller ionic radii as B'4 + cations and prefer a

6-fold coordinated environment, Zr and Hf possess relatively larger tetravalent ionic radii and have a strong preference for a 7-fold coordinated environment. We note that the chemical

propensity for a 7-fold coordination for Hf and Zr is also a reason for the monoclinic ground states of simple oxides of these metals, _i_._e_., HfO2 and ZrO2, where the metal ions are

7-fold coordinated. These notions are further illustrated in Fig. 6. While Fig. 6a qualitatively depicts the geometrical similarity of a 7-fold coordination for Hf atom in a double

pyrochlore to that in HfO2, the partial density of states (DOS) for Hf presented in Fig. 6b, quantitatively confirms this by comparing electronic structures of 7-fold coordinated Hf atoms in

HfO2 and Gd2(Ti0.25Hf0.75)2O7, respectively. Qualitatively similar results are also obtained for the corresponding Zr-based chemistries. It is also worthwhile to note here that the

stabilization achievable through the O relaxations in mixed pyrochlore chemistries is asymmetry with respect to B and B’ cation species. More specifically, for an A2(B0.25B'0.75)2O7

compound only certain B’ cations can change their coordination from 6-fold to 7-fold as a result of the O relaxations, while all the B cations remain 6-fold coordinated. Therefore, energetic

contributions resulting from the O relaxations to the mixing energies (as shown in Fig. 5b) are predominantly governed by the chemical propensity of the B’ cations towards a 7-fold

coordination. This implies that for chemistries containing both Hf and Zr on the B-sublattice—such as A2(Hf0.25Zr0.75)2O7 and A2(Zr0.25Hf0.75)2O7—the coordination change of the B’ cations

(Zr in the former case and Hf in the latter case) is largely responsible for the lowering of the mixing energies. As a result of the relaxation displacements of the O atom, the compounds

with Zr and Hf atoms at the B’ site are not only able to satisfy their natural propensity for a 7-fold B’ coordination, but also the appropriate ionic size of these cation species allows for

minimization of the local strains caused as result of the O displacements. This is in contrast to the compounds with Ti and Sn as B’ cations. While both Ti4+ and Sn4+ ions intrinsically

prefer a 6-fold coordination, the much smaller ionic radius of Ti4+, as compared to the Zr4+ and Hf4+, further results in energetically unfavorable local strains in case of the O

displacements, leading to relatively larger positive energies of mixing in comparison to the corresponding Sn based compounds. DISCUSSION These findings have important implications for ionic

conductivity in pyrochlores and provide insights into previously observed but yet to be explained trends. For example, Fig. 7 shows experimentally measured ionic conductivities in mixtures

of Y2Ti2O7 and Y2Zr2O7 as a function of both temperature and relative Zr content. Consistent with other studies on mixed Gd2Ti2O7 and Gd2Zr2O7, the conductivity is relatively low for the

pure Ti compound and increases with increasing Zr content _y_. Most interestingly, however, is that the conductivity is not a monotonic function of _y_ but rather exhibits a small dip at a

composition of _y_ = 0.8. The size of this dip is temperature dependent. This result suggests that there is some aspect of this composition that is different from the neighboring ones. We

suggest that this composition might exhibit an ordered structure of Ti and Zr. Indeed, our DFT calculations indicate that for compositions around _y_ = 0.75 the propensity for such ordering

is greatest. We cannot rule out that other effects might be driving this experimental behavior, such as differences in phase separation. Also, the cation mixing in the experimental system

may be more complex than we have examined, with mixing between the A and B cations as well. However, it is intriguing that there is some reduction of conductivity at the composition where we

predict there to be the greatest ordering. In fact, the presence of 7-fold coordinated Zr would be expected to lead to a reduction of conductivity as it would tend to be a bottleneck for

the passage of an oxygen vacancy. As mentioned in the introduction, mixed pyrochlores have been used as a way of systematically introducing disorder into the compound to examine the effects

on ionic conductivity, with conflicting results. Our results suggest that, in addition to introducing two changes to the system at once–a change in chemistry as well as disorder–there may be

other effects, such as compositional ordering, that further complicate analysis and comparison. This is also born out by the measurements on mixed Y2Ti2O7-Y2Zr2O7 discussed above. Thus,

there are potential complications to chemical changes that must be considered when interpreting the results from experiments on mixed pyrochlores. Indeed, changes in Zr coordination, in

which Zr goes from a 6-fold to a 7-fold coordination in the pyrochlore matrix, have been observed before in various experimental studies.28,29,30 However, in all cases, these changes have

been induced by cation mixing and the associated changes in the oxygen distribution. Further, in those studies, any increase in Zr coordination was accompanied by decreases in the

coordination of other cations. To the best of our knowledge, our theoretical calculations are the first to demonstrate the stabilization of an ordered structure because of the shift in

coordination of Zr. Finally, our results provide some insight into the fundamental difference in the ionic conductivity in Zr-based pyrochlores as compared to Ti-based compounds. In

pyrochlores in which B = Ti, all of the B cations are 6-fold coordinated, as they prefer to be. This essentially locks the oxygen in place, as any movement would disrupt, at least

temporarily, the coordination of the Ti cations. However, in the case of B = Zr, the B cations would prefer to have 7-fold coordination. Thus, the system is, in some sense, frustrated. All

of the Zr cations would prefer a higher coordination, and that can be achieved at least transiently by shifting oxygen around. This cannot be done for all Zr simultaneously and so leads to a

system that is more dynamic than if B = Ti. Thus, the origin of higher conductivity in Zr compounds is not due to a stronger Ti-O bond, but rather a stronger Zr–O interaction that drives

the system to constantly shift the oxygen around in a frustrated attempt to increase the Zr coordination. This may lead to longer-range concerted events that drive ionic conductivity in this

type of system. Such effects have been proposed earlier by Mohn et al. in the context of ionic conductivity in Ba2In2O5.31 To conclude, we have found novel low-energy ordered structures for

the mixed Gd2Ti2O7–Gd2Zr2O7 pyrochlores. The lowest energy structures are stabilized by an oxygen relaxation that allows for 7-fold coordination of some of the Zr cations in these

structures. This result has implications not only for interpreting experimental results on mixed pyrochlores, but also on the origins of conductivity in these types of systems. Finally, the

potential presence of ordered structures in mixed pyrochlores opens a new avenue for tailoring the properties of these systems, in much the same way that is being explored for double

perovskites. So-called double pyrochlores extend the functional space of these compounds. METHODS DFT calculations were performed using the Vienna _Ab initio_ Simulation Package (VASP)32,33

and employed the Perdew, Burke, and Ernzerhof (PBE)34 generalized gradient approximation (GGA) exchange-correlation functional. The electronic wave functions were expanded in plane waves up

to a cut-off energy of 600 eV. The pseudopotentials based on the projector augmented wave method35 explicitly included the following valence electronic configurations for different elemental

species in Gd2(Zr_x_Ti1−_x_)2O7 chemistries; Gd: 5_p_65_d_16_s_2, Ti: 3_p_63_d_2 4_s_2, Zr: 4_s_24_p_64_d_25_s_2, and O: 2_s_22_p_4. A Gamma-centered automatically-generated 4 × 4 × 4

Monkhorst-Pack _k_-point mesh36 was used for Brillouin-zone integrations for a supercell containing 22 atoms. For larger supercells, the _k_-point meshes were appropriately scaled to give

the same _k_-point density in the reciprocal space. Spin-unpolarized calculations were employed at large, however tests with spin-polarized calculations were also performed to confirm both

the relative energetics and chemical trends computed with the spin-unpolarized calculations. To obtain a geometry optimized equilibrium structure, atomic positions as well as the supercell

lattice parameters were fully relaxed using the conjugate gradient method until all the Hellmann-Feynman forces and the stress component were less than 0.02 eV/Å and 1.0 × 10−2 GPa,

respectively. The enumeration of different Gd2(Zr_x_Ti1−_x_)2O7 chemistries and orderings over the parent crystal structure was performed with the CASM software package

[https://github.com/prisms-center/CASMcode].23,37,38 The primitive cells employed for the mixed pyrochlore chemistries contained 22 atoms and configurations spanned by supercells containing

up to 66 atoms were enumerated exhaustively. This enumeration resulted in a total of 704 different configurations, for which total energy minimizations and computations were performed within

DFT. Different configurations represent different arrangements of Ti and Zr on the B sublattice within the pyrochlore structure. An effort was also made using CASM to construct and

parametrize cluster expansion (CE) Hamiltonians in order to perform subsequent finite temperature Monte Carlo simulations.39,40,41,42 However, as discussed further in the results section,

large basis deformations encountered during structural relaxations for a subset of Gd2(Zr_x_Ti1−_x_)2O7 chemistries prevented us from fitting CE Hamiltonians reproducing the relative

energetics of DFT computations with a high fidelity. To evaluate the relative tendency of B-site mixing in different pyrochlores as a function of chemistry, mixing energies of 132 “double”

pyrochlores (each containing a single A-site and two different B-site cations) were computed. Specifically, the 11 element choices considered for the A-site chemistry were Y, La, Pr, Nd, Sm,

Gd, Tb, Dy, Ho, Er and Lu, while the two different elements mixing on the B sub-lattice were selected form a pool of four species, _viz_., Ti, Zr, Sn and Hf. For these elements, the

specific choices of the VASP pseudopotentials (along with the associated number of valance electrons) employed in the DFT computations are listed in Table 1. Since an explicit exhaustive

enumeration—similar to that for the Gd2(Zr_x_Ti1−_x_)2O7 chemistries described above—for the entire set of 132 double pyrochlores is well beyond the scope of the present work, for practical

reasons, we simulated the double pyrochlores in a composition and configuration that resulted in the lowest energy of mixing for the Gd2(Zr_x_Ti1−_x_)2O7 chemistries. DATA AVAILABILITY The

data that support the findings of this study are available from the corresponding authors upon reasonable request. REFERENCES * Kimble, T., Chou, M. & Chai, B. Scintillation properties

of LYSO crystals. _IEEE Nucl. Sci. Symp. Conf. Rec._ 3, 1434–1437 (2002). Google Scholar  * Fukushima, T., Stroppa, A., Picozzi, S. & Perez-Mato, J. M. Large ferroelectric polarization

in the new double perovskite NaLaMnWO6 induced by non-polar instabilities. _Phys. Chem. Chem. Phys._ 13, 12186 (2011). Article  CAS  Google Scholar  * Pilania, G. & Uberuaga, B. P.

Cation ordering and effect of biaxial strain in double perovskite CsRbCaZnCl. _J. Appl. Phys._ 117, 114103 (2015). Article  Google Scholar  * Heitmann, A. A. & Rossetti, G. A.

Thermodynamics of ferroelectric solid solutions with morphotropic phase boundaries. _J. Am. Ceram. Soc._ 97, 1661 (2014). Article  CAS  Google Scholar  * Rost, C. M. et al.

Entropy-stabilized oxides. _Nat. Commun._ 6, 8485 (2015). Article  CAS  Google Scholar  * Suntivich, J., May, K. J., Gasteiger, H. A., Goodenough, J. B. & Shao-Horn, Y. A perovskite

oxide optimized for oxygen evolution catalysis from molecular orbital principles. _Science_ 334, 1383 (2011). Article  CAS  Google Scholar  * Vasala, S. & Karppinen, M.

A2B'B''O6 perovskites: a review. _Prog. Solid State Chem._ 43, 1 (2015). Article  CAS  Google Scholar  * Karppinen, M. & Yamauchi, H. In (Ed. Narlikar, A. V.) _Frontiers

in Magnetic Materials_ 153–184 (Springer-Verlag, Berlin, 2005). * King, G. & Woodward, P. M. Cation ordering in perovskites. _J. Mater. Chem._ 20, 5785 (2010). Article  CAS  Google

Scholar  * Davies, P., Wu, H., Borisevich, A., Molodetsky, I. & Farber, L. Crystal chemistry of complex perovskites: new cation-ordered dielectric oxides. _Annu. Rev. Mater. Res._ 38,

369 (2008). Article  CAS  Google Scholar  * Howard, C. J., Kennedy, B. J. & Woodward, P. M. Ordered double perovskites - a group-theoretical analysis. _IUCr. Acta Crystallogr. Sect. B

Struct. Sci._ 59, 463 (2003). Article  Google Scholar  * Goodenough, J. B. Electronic and ionic transport properties and other physical aspects of perovskites. _Rep. Progress. Phys._ 67,

1915 (2004). Article  CAS  Google Scholar  * Uberuaga, B. P. & Pilania, G. Effect of cation ordering on oxygen vacancy diusion pathways in double perovskites. _Chem. Mater._ 27, 5020

(2015). Article  CAS  Google Scholar  * Serrate, D., Teresa, J. M. D. & Ibarra, M. R. Double perovskites with ferromagnetism above room temperature. _J. Phys. Condens. Matter_ 19, 023201

(2007). Article  Google Scholar  * Sickafus, K. E. et al. Radiation tolerance of complex oxides. _Science_ 289, 748 (2000). Article  CAS  Google Scholar  * Lang, M. et al. Structural

modifications of Gd2Zr2- xTixO7 pyrochlore induced by swift heavy ions: disordering and amorphization. _J. Mater. Res._ 24, 1322 (2009). Article  CAS  Google Scholar  * Hess, N. J. et al.

Spectroscopic investigations of the structural phase transition in Gd2(Ti1-yZry)2O7 pyrochlores. _J. Phys. Chem. B_ 106(18), 4663–4677 (2002). Article  CAS  Google Scholar  * Tuller, H. L.

J. Oxygen ion conduction and structural disorder in conductive oxides. _Phys. Chem. Solids_ 55, 1393 (1994). Article  CAS  Google Scholar  * Díaz-Guillén, J. et al. The effect of homovalent

A-site substitutions on the ionic conductivity of pyrochloretype Gd2Zr2O7. _J. Power Sources_ 186, 349 (2009). Article  Google Scholar  * Moreno, K. J. et al. Influence of thermally induced

oxygen order on mobile ion dynamics in Gd2(Ti0.65Zr0.35)2O7. _Phys. Rev. B_ 75, 184303 (2007). Article  Google Scholar  * Reader, S. W. et al. Cation disorder in pyrochlore ceramics: Y MAS

NMR and first-principles calculations. _J. Phys. Chem. C._ 113, 18874 (2009). Article  CAS  Google Scholar  * Fernandes, A. et al. Phase composition and disorder in La (Sn,Ti) O ceramics:

new insights from NMR crystallography. _J. Phys. Chem. C._ 120, 20288 (2016). Article  CAS  Google Scholar  * Thomas, J. C. & der Ven, A. V. Finite-temperature properties of strongly

anharmonic and mechanically unstable crystal phases from rst principles. _Phys. Rev. B_ 88, 214111 (2013). Article  Google Scholar  * Uberuaga, B. P. & Sickafus, K. E. Interpreting

oxygen vacancy migration mechanisms in oxides using the layered structure motif. _Comput. Mater. Sci._ 103, 216 (2015). Article  CAS  Google Scholar  * O’Keeffe, M. & Hyde, B. G. Plane

nets in crystal chemistry. _Philos. Trans. R. Soc. A: Math., Phys. Eng. Sci._ 295, 553 (1980). Article  Google Scholar  * Slater, J. C. Atomic radii in crystals. _J. Chem. Phys._ 41, 3199

(1964). Article  CAS  Google Scholar  * de los Reyes, M. et al. The pyrochlore to defect fluorite phase transition in Y2Sn2-xZrxO7. _RSC Adv._ 3, 5090 (2013). Article  Google Scholar  * Liu,

Y., Withers, R. L. & Noren, L. The pyrochlore to ‘defect fluorite’ transition in the Y2(ZryTi1−y)2O7 system and its underlying crystal chemistry. _J. Solid State Chem._ 177, 4404

(2004). Article  CAS  Google Scholar  * Norberg, S. T. et al. Pyrochlore to fluorite transition: the Y2(Ti1–xZrx)2O7 (0.0 ≤ x ≤ 1.0) system. _Chem. Mater._ 24, 4294 (2012). Article  CAS 

Google Scholar  * Zhang, Z. et al. Gradual structural evolution from pyrochlore to defect-fluorite in Y2Sn2–xZrxO7: average vs local structure. _J. Phys. Chem. C._ 117, 26740 (2013). Article

  CAS  Google Scholar  * Mohn, C. E., Allan, N. L., Freeman, C. L., Ravindran, P. & Stølen, S. Order in the disordered state: local structural entities in the fast ion conductor

Ba2In2O5. _J. Solid State Chem._ 178, 346 (2005). Article  CAS  Google Scholar  * Kresse, G. & Furthmüller. Efficient iterative schemes for ab initio total-energy calculations using a

planewave basis set. _J. Phys. Rev. B_ 54, 11169 (1996). * Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. _Phys. Rev. B_ 59, 1758

(1999). Article  CAS  Google Scholar  * Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. _Phys. Rev. Lett._ 77, 3865 (1996). Article  CAS  Google

Scholar  * Blöchl, P. E. Projector augmented-wave method. _Phys. Rev. B_ 50, 17953 (1994). Article  Google Scholar  * Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone

integrations. _Phys. Rev. B_ 13, 5188 (1976). Article  Google Scholar  * Puchala, B. & Van der Ven, A. Thermodynamics of the Zr-O system from rst-principles calculations. _Phys. Rev. B_

88, 094108 (2013). Article  Google Scholar  * Van der Ven, A., Thomas, J., Xu, Q. & Bhattacharya, J. Linking the electronic structure of solids to their thermodynamic and kinetic

properties. _Math. Comput. Simul._ 80, 1393 (2010). Article  Google Scholar  * Sanchez, J., Ducastelle, F. & Gratias, D. Generalized cluster description of multicomponent systems. _Phys.

A: Stat. Mech. its Appl._ 128, 334 (1984). Article  Google Scholar  * Sanchez, J. M. Cluster expansion and the congurational theory of alloys. _Phys. Rev. B_ 81, 224202 (2010). Article 

Google Scholar  * Asta, M., Wolverton, C., de Fontaine, D. & Dreyssé, H. Effective cluster interactions from cluster-variation formalism. _Phys. Rev. B_ 44, 4907 (1991). Article  CAS 

Google Scholar  * Fontaine, D. D. Cluster approach to order-disorder transformations in alloys. _Solid State Phys._ 47, 33 (1994). Article  CAS  Google Scholar  * Crystal Diffract 6.

http://crystalmaker.com/crystaldiffract/. * Mathew, K. et al. A materials project based Python tool for high-throughput computational screening of interfacial systems. _Comput. Mater. Sci._

122, 183 (2016). Article  CAS  Google Scholar  * Heremans, C., Wuensch, B. J., Stalick, J. K. & Prince, E. Fast-ion conducting Y2(ZryTi1-y)2O7 pyrochlores: neutron Rietveld analysis of

disorder induced by Zr substitution. _J. Solid State Chem._ 117, 108 (1995). Article  CAS  Google Scholar  Download references ACKNOWLEDGEMENTS We thank Neil Allan for useful discussions and

the group of Richard G. Hennig for help in orthogonalizing the structure used in the simulation of the XRD pattern shown in Fig. 2. BPU and GP were supported by the U.S. Department of

Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division. The work was performed at the Los Alamos National Laboratory (LANL), an affirmative action

equal opportunity employer, operated by Los Alamos National Security, LLC, for the National Nuclear Security Administration of the U.S. DOE under contract DE-AC52-06NA25396. Computational

support for this work was provided by LANL’s high performance computing clusters. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Materials Science and Technology Division, Los Alamos National

Laboratory, Los Alamos, NM, 87545, USA Ghanshyam Pilania & Blas P. Uberuaga * Materials Science and Engineering Department, University of Michigan, Ann Arbor, MI, 48109, USA Brian

Puchala Authors * Ghanshyam Pilania View author publications You can also search for this author inPubMed Google Scholar * Brian Puchala View author publications You can also search for this

author inPubMed Google Scholar * Blas P. Uberuaga View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS B.P.U. designed the study. G.P. and

B.P.U. performed the high-throughput computations and wrote the manuscript. B.P. helped with CASM computations and analysis of the results. All authors discussed the results and commented on

the manuscript. CORRESPONDING AUTHORS Correspondence to Ghanshyam Pilania or Blas P. Uberuaga. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no Competing Interests. ADDITIONAL

INFORMATION PUBLISHER’S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY

INFORMATION RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution

and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if

changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the

material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to

obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS

ARTICLE Pilania, G., Puchala, B. & Uberuaga, B.P. Distortion-stabilized ordered structures in A2BB’O7 mixed pyrochlores. _npj Comput Mater_ 5, 7 (2019).

https://doi.org/10.1038/s41524-018-0144-1 Download citation * Received: 23 July 2018 * Accepted: 12 December 2018 * Published: 14 January 2019 * DOI:

https://doi.org/10.1038/s41524-018-0144-1 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative