Out-of-sample extrapolation utilizing semi-supervised manifold learning (ose-ssl): content based image retrieval for histopathology images

ABSTRACT Content-based image retrieval (CBIR) retrieves database images most similar to the query image by (1) extracting quantitative image descriptors and (2) calculating similarity

between database and query image descriptors. Recently, manifold learning (ML) has been used to perform CBIR in a low dimensional representation of the high dimensional image descriptor

space to avoid the curse of dimensionality. ML schemes are computationally expensive, requiring an eigenvalue decomposition (EVD) for every new query image to learn its low dimensional

representation. We present out-of-sample extrapolation utilizing semi-supervised ML (OSE-SSL) to learn the low dimensional representation without recomputing the EVD for each query image.

OSE-SSL incorporates semantic information, partial class label, into a ML scheme such that the low dimensional representation co-localizes semantically similar images. In the context of

prostate histopathology, gland morphology is an integral component of the Gleason score which enables discrimination between prostate cancer aggressiveness. Images are represented by shape

features extracted from the prostate gland. CBIR with OSE-SSL for prostate histology obtained from 58 patient studies, yielded an area under the precision recall curve (AUPRC) of 0.53 ± 0.03

comparatively a CBIR with Principal Component Analysis (PCA) to learn a low dimensional space yielded an AUPRC of 0.44 ± 0.01. SIMILAR CONTENT BEING VIEWED BY OTHERS ADVANCING PROSTATE

CANCER DETECTION: A COMPARATIVE ANALYSIS OF PCLDA-SVM AND PCLDA-KNN CLASSIFIERS FOR ENHANCED DIAGNOSTIC ACCURACY Article Open access 23 August 2023 ENHANCING MULTICLASS BRAIN TUMOR DIAGNOSIS

USING SVM AND INNOVATIVE FEATURE EXTRACTION TECHNIQUES Article Open access 29 October 2024 METRICS RELOADED: RECOMMENDATIONS FOR IMAGE ANALYSIS VALIDATION Article 12 February 2024

INTRODUCTION Manual examination of prostate histopathology by an expert pathologist is the current gold standard for prostate cancer diagnosis, with roughly 242,000 new cases ever year1. The

most common system of grading prostate cancer is the Gleason score2, determined as a summation of the two most prevalent Gleason patterns. Low Gleason grade patterns (1–3) are reflective of

less aggressive disease while high Gleason grade patterns (4–5) are reflective of more aggressive disease. The most dominant Gleason patterns, comprising around 90% of needle biopsies

cases, are patterns 3 and 43. Correctly distinguishing between primary Gleason patterns 3 and 4 is critical for determining the appropriate treatment for patients; patients with less

aggressive disease (primary Gleason grade patterns ≤3) are enrolled in active surveillance programs while patients with more aggressive disease (primary Gleason grade patterns ≥4) undergo

treatment4. Additionally, distinguishing between the intermediate Gleason patterns 3 and 4 is a particularly challenging task, with inter-observer agreement between pathologists as low as

0.47–0.64 (reflecting low to moderate agreement). Hence a method to consistently distinguish between these patterns is an important clinical need5. Prostate glands are considered an

important substructure when assessing Gleason grade2 and gland morphology has been shown to discriminate between benign and malignant tissue regions6,7,8. A content-based image retrieval

(CBIR) system which can accurately retrieve prostate histopathology according to Gleason grade pattern can be useful in a clinical, research and educational setting. To enable ease of

reading Table 1 lists common acronyms used throughout this manuscript. An accurate CBIR system for retrieval of Gleason grade patterns can aid in the training of medical students and could

allow pathology residents to hone in on their Gleason grading skills6,7,9. In this work we present Out-of-Sample Extrapolation utilizing Semi-Supervised Learning (OSE-SSL) for CBIR of

prostate histopathology. OSE-SSL allows for CBIR of the prostate histopathology images to be performed in an accurate and computationally efficient manner. To determine image similarity we

leverage our previously developed method, Explicit Shape Descriptors (ESDs)8, to distinguish between prostate glands from different Gleason grade patterns. ESDs involve fitting an explicit

medial axis shape model to each gland of interest, computing pairwise differences between shape models and then extracting a set of feature via manifold learning (ML). ESDs have been shown

to have over 80% classification accuracy in distinguishing prostate glands belonging to Gleason grade patterns 3 and 48. This current work is distinct from8 due to the following reasons: (1)

in this paper we present a computationally efficient method (OSE-SSL) for retrieving images in a low dimensional representation of the feature space, while in8 the methodology for ESDs

extraction was presented; (2) in this paper we focus on evaluating OSE-SSL in terms of computational efficiency and precision-recall accuracy, while in8 we focused specifically on the

classification accuracy of ESDs; and (3) OSE-SSL is a method that can be used in conjunction with any set of image features, while in8 ESDs are a specific method of extracting morphologic

features from an object of interest. CBIR systems attempt to retrieve images from a database identified as being the most similar to the query image in terms of quantitative image

descriptors obtained from the query and database images. In the context of medical imagery, images which are visually similar often have similar pathologies. A CBIR system for histopathology

images could serve as a useful training tool for pathology residents, fellows and medical students and could potentially serve as a decision-support tool in diagnosis and grading of

pathologies6,7,9,10,11,12,13,14,15,16. CBIR systems are particularly relevant in the context of histopathology imagery where (a) the images can be extremely large and described by a very

large set of image descriptors and (b) differences between pathologies may be very subtle and not immediately appreciable visually. Additionally, with the recent advent of whole-slide

digital scanners, pathology labs will soon be routinely generating very large amounts of digitized histopathology imagery, necessitating intelligent and efficient image retrieval systems17.

CBIR systems typically comprise two components: (1) a module for extraction of domain specific image descriptors to quantitatively characterize the images and (2) a module for computation of

the similarity between the query and database images in terms of the quantitative image descriptors. Histopathology images typically comprise several billions worth of pixels17 and hence

histopathology CBIR systems require a large number of image descriptors to accurately describe subtle differences in the complex imagery6,7,9,10,12,13,14,15,16. Such medical imagery can be

represented by a high dimensional space, where each dimension corresponds to a single image descriptor. A high dimensional image descriptor space makes the calculation of similarity between

image descriptors difficult as (a) the number of database images may be small compared to the number of image descriptors giving rise to the curse of dimensionality problem18 and (b) images

often cluster densely in small regions of the high dimensional space19. Hence relationships between image descriptors may be important when calculating image similarity. Consequently, a few

researchers have proposed dimensionality reduction (DR) methods6,7,9,10,16,20 to map the high dimensional image descriptors into a low dimensional representation so that image similarity

calculation and retrieval can be performed directly in the low dimensional space. Retrieval performed in a low dimensional space is often more accurate than retrieval performed in the

original high dimensional space6,7. However, utilizing DR methods to learn a low dimensional space may add computational complexity to the retrieval algorithm. Linear DR methods, such as

Principal Component Analysis (PCA), attempt to find a low dimensional space that is a linear projection of the high dimensional space. Hence linear DR methods only preserve linear

relationships between images9,10. Semi-supervised learning (SSL) methods, such as Linear Discriminant Analysis (LDA), have been proposed to take into account semantic information such as

partial class labels when learning a low dimensional projection in order to co-localize semantically similar images13,21,22. However, these methods assume that a linear projection of the

high dimensional space will best preserve relationships between images. ML schemes attempt to find a low dimensional embedding space which preserves the manifold structure of the image

descriptors in the high dimensional space. Hence ML methods attempt to preserve the non-linear relationships between image descriptors23,24,25. Graph Embedding (GE)23, a specific instance of

a ML scheme, attempts to model the manifold structure using local, pairwise relationships between image descriptors in the high dimensional space thereby preserving these relationships

between images in the low dimensional space. Recent work has demonstrated that ML schemes, such as GE, may result in low dimensional spaces better suited for CBIR when image similarity is

defined by a non-linear manifold in the high dimensional space6,7,16,20. Semi-supervised ML methods, which utilize SSL in conjunction with ML, attempt to learn a low dimensional embedding

space such that semantic, non-linear relationships between images in the high dimensional space are preserved26. To our knowledge no CBIR systems for histopathology have leveraged SSL.

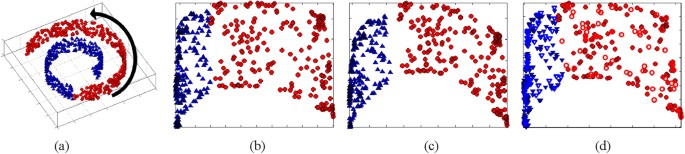
However, CBIR systems for color photography20,27 have been proposed which leverage such methods. Figure 1 demonstrates the ability of GE to preserve non-linear relationships between samples

for the synthetic Swiss Roll dataset. Figure 1(a) shows a synthetic Swiss Roll dataset consisting of 2000 samples described by a 3_D_ space, the arrow demonstrating the direction of greatest

variance along the manifold. In this example GE is able to find a low dimensional space (2_D_) which preserves the underlying structure of the dataset as evidenced by the planar 2_D_

embedding space shown in Fig. 1(b). Figure 1(c) shows the results of semi-supervised GE (SSGE) for the Swiss Roll. Note that for SSGE (Fig. 1(c)) samples from two classes (blue, red) have a

larger separation compared to GE (Fig. 1(b)). Despite the advantages of ML, only a few papers have attempted to use ML in conjunction with CBIR of medical imagery6,7,16, due to its

computational cost. A computationally expensive eigenvalue decomposition (EVD) must be calculated for every new query image28,29. Hence there is a need to develop ML schemes which are more

computationally efficient and do not require a EVD for each new query image. Algorithms have been developed to avoid recomputing the EVD for out-of-sample images, but have not previously

been evaluated in the context of CBIR for medical imagery28,29. Locality Preserving Projections (LPP) attempts to approximate the low dimensional embedding space found by ML as a linear

combination of image descriptors in the high dimensional space28. LPP is reliant on a linear combination of the image descriptors accurately modeling relationships between images and hence

accurately modeling relationships in the low dimensional space. If the low dimensional space found via ML is not approximately linear LPP will not correctly estimate the low dimensional

space. Alternatively, out-of-sample extrapolation (OSE)29 attempts to determine the location (or embedding) of a new query image in the low dimensional embedding space as a weighted sum of

the embeddings already calculated for a set of images. In the context of a CBIR system, the calculated embeddings would correspond to the locations for the database images. Unlike LPP,

non-linear relationships between images are preserved and, hence, OSE may be better able to resolve differences between images belonging to different classes. Figure 1(d) shows the result of

OSE for the Swiss Roll dataset where samples projected into the low dimensional space via OSE are represented by open points. In this paper we present OSE-SSL a novel and unique combination

of SSL13,21,22 and OSE29 into a unified framework. The OSE-SSL algorithm represents a novel, non-obvious combination of these two popular methods. The OSE-SSL algorithm first refines

relationships between images in the low dimensional embedding space according to semantic information via SSL and then utilizes OSE to project never before seen images into the low

dimensional space learned via SSL. PREVIOUS WORK AND NOVEL CONTRIBUTIONS Several CBIR methods for radiological medical imagery have been presented21,30. Such CBIR systems extract relatively

few image descriptors and hence are able to accurately perform image retrieval in the original high dimensional image descriptor space. In comparison, CBIR systems for histopathology imagery

extract a very large number of features to describe the complex imagery6,7,9,10,12,13,14,15,16,31,32,33,34,35,36 and therefore typically perform image retrieval in a reduced dimensional

space to overcome the curse of dimensionality problem. Comaniciu _et al_.10 utilized a weighted sum of image descriptors, where weights were determined by maximizing an objective function,

to retrieve images corresponding to different hemotologic malignancies. This approach is equivalent to a linear DR method as only linear relationships between images are preserved during

retrieval. Yang _et al_.15 utilized a similar approach on a larger database of hemotologic malignancies. Similarly Zhang _et al_.32 determined a weighted sum of image descriptors using a

Pareto archived evolution strategy to learn the best weights for their image retrieval task. Zheng _et al_.9 utilized multi-dimensional scaling (MDS), a linear DR scheme, to compute a low

dimensional space in which image retrieval could be performed for a set of histopathology images taken from different anatomical regions (e.g. spleen, prostate, colon, etc.). Tang _et al_.12

obtained different low dimensional spaces by considering different image descriptors, to obtain a corresponding set of semantic labels. Image retrieval of colon histopathology images was

then performed by returning images with the most similar semantic labels across the different low dimensional spaces. Yu _et al_.14 took a similar approach but introduced spatial constraints

to determine the semantic labels and image similarity for colon histopathology images. Caicedo _et al_.31 used a non-negative matrix factorization to determine a mapping between image

features and semantic terms; new images could be projected into the learned feature space to retrieve similar images. Lessmann _et al_.13 used self organizing maps to determine the most

important image descriptors for meningioma histopathology; the top 6 image descriptors were selected to determine image similarity. Caicedo _et al_.16 determined similarity between

basal-cell carcinoma histopathology images by learning a set of kernels and associated weights for each image descriptors. Such a scheme is equivalent to ML, as non-linear relationships

between image descriptors are taken into account. This method required an extensive offline training phase to learn the kernels and weights utilized in the similarity measure. Zhang _et

al_.33,35 use a semi-supervised hashing method in combination with a set of kernels to learn a non-linear feature space that can quickly and efficiently describe feature similarity between

images using SIFT features. Zhang _et al_.36 applied a semi supervised hashing method to cell-based features for image retrieval of histpathology images. Jiang _et al_.34 used a similar

hashing method, but used a joint kernel representation for both image features and labels to learn a hash representation that could better model class relationships between images. Previous

work from our group used GE to find a low dimensional embedding space and then retrieved prostate histopathology images according to image similarity in the low dimensional space6. This

method was able to take into account non-linear relationships between image samples without an extensive offline learning phase. However, GE must recalculate a computationally expensive EVD

for every out-of-sample image, or every query image not contained in the database images. In this work we have developed OSE-SSL algorithm, which represents a novel combination of SSL and

OSE, designed specifically to be computationally tractable. The novel integration of these two methods involves projecting never-before seen images into a low dimensional embedding space

that takes into account semantic information (class label information). Hence OSE-SSL (a) integrates known label information to learn a low dimensional embedding space and (b) overcomes the

out-of-sample problem. We demonstrate the use of OSE-SSL in the context of CBIR applications. Figure 2 illustrates a flowchart of our OSE-SSL CBIR system. The CBIR system is characterized by

(1) offline database construction where SSL is applied to quantitative image descriptors for a set of database images to obtain a low dimensional embedding space and (2) online image

retrieval where OSE is used to compute the embedding location of a never before seen query image. Offline database construction consists of (a) extracting image descriptors for all database

images and (b) applying SSL to determine the low dimensional embedding space for images contained within the database. Once offline database construction has been completed online image

retrieval is then performed efficiently utilizing OSE. Online image retrieval consists of (c) extracting image descriptors from the query image, (d) OSE of the query image into the low

dimensional embedding space and (e) ranking image similarity in the low dimensional embedding space. The novelty of OSE-SSL is four-fold: (1) OSE-SSL leverages partial class label

information, where available, when learning the low dimensional space by utilizing SSL, (2) OSE-SSL extrapolates a new query image into the low dimensional space without re-computing an EVD

by utilizing OSE, making OSE-SSL computationally tractable compared to SSL and hence, ideally suited to CBIR applications, (3) OSE-SSL represents a novel, non-obvious combination of OSE and

SSL into a single unified framework and (4) OSE-SSL is demonstrated in the context of a novel application of CBIR to the Gleason grading problem. In this work, we demonstrate the application

of OSE-SSL to a CBIR system which retrieves images according to morphologic similarity. Morphologic similarity is determined via ESDs, a morphologic descriptor which is determined by (1)

fitting a medial axis shape model to each shape, (2) determining pairwise similarity between images and (3) performing non-linear dimensionality reduction on the pairwise similarity8. We

evaluate our system on two datasets a digitized prostate histopathology dataset. The prostate histopathology dataset was chosen due to the challenges in accurately distinguishing between

intermediate Gleason grade patterns5; ESDs have been shown to have over 80% classification accuracy in distinguishing between prostate glands from Gleason grade pattern 3 and Gleason grade

pattern 4 as seen on histopathology8. Hence a CBIR system which leverages ESDs should be able to accurately retrieve histopathology images according to Gleason grade pattern. OUT-OF-SAMPLE

EXTRAPOLATION UTILIZING SEMI-SUPERVISED MANIFOLD LEARNING (OSE-SSL) NOTATION Table 2 displays the notation used in the paper. A database of _N_ images is defined by . _r_ denotes that the

image is contained in C, to contrast with where _q_ denotes a query image not contained in database. Each image in the database has a corresponding label defined by L = [_l_1, …, _l__N_].

Every label _l__i_ ∈ L takes on a discrete value _l__i_ ∈ {1, 2, …, _Z_} where C contains images belonging to _Z_ classes. For two images and , _j_ ≠ _i_ we define pairwise dissimilarity as

. The function ϕ(·, ·) can represent any dissimilarity function such that if then it follows that and are more dissimilar than and . The function is evaluated over all _i, j_ ∈ {1, …, _N_},

_j_ ≠ _i_ to obtain _A. A_ is an _N_ × _N_ matrix representing pairwise dissimilarity between all images contained in C. REVIEW OF MANIFOLD LEARNING GRAPH EMBEDDING The goal of GE is to

determine a set of low dimensional embedding locations that preserves the relationships between images in where . GE determines Y by modeling the similarity between images according to a

similarity matrix _W_. Given the dissimilarity matrix _A_ described in the Notation Section, _W_ is found by _W_(_i, j_) = _e_−_A_(_i, j_)/σ, where σ is a user selected scaling parameter. Y

is then found by minimizing the pairwise reconstruction error defined as, where ||·||2 denotes the L2-norm. An image is associated with the embedding location _y__i_. Belkin _et al_.37

demonstrated that Equation 1 is equivalent to the following eigenvalue decomposition (EVD), where _D_ is a diagonal matrix defined as . The smallest _d_ eigenvalues, excluding any 0 valued

eigenvalues, in λ correspond to the _d_ eigenvectors Y which are defined as the _d_ dimensional embedding locations. Y correspond to the projection of the matrix _W_ into such that the

pairwise similarity between the elements in _W_ and hence the pairwise similarity between images, are preserved. Furthermore the eigenvectors Y are orthonormal, hence, each additional

eigenvector (or dimension) provides independent information on the image similarity in _W_. SEMI-SUPERVISED MANIFOLD LEARNING (SSL) For C let a corresponding set of known labels be defined

as L_r_ ⊂ L where L_r_ = [_l_1, …, _l__M_]. Note that _M_ < _N_ as we assume that some labels may be unknown for images contained in C. A similarity matrix _W__r_ is constructed by

altering elements in _W_ according to L_r_. Images which correspond to the same class have higher values in _W__r_ compared to _W_, while images which correspond to different classes have

lower values in _W__r_ compared to _W_. For images where no label information is known the values in _W__r_ and _W_ are equivalent. _W__r_ is calculated as, where γ = _W_(_i, j_). The

“otherwise” case corresponds to instances where label information is unknown for either _l__i_ or _l__j_. Once the similarity matrix _W__r_ has been calculated, the EVD described by Equation

2 is performed on _W__r_ to obtain Y_r_. By altering _W__r_ according to Equation 3, images belonging to the same class (i. e. _l__i_ = _l__j_) will be close together in the low dimensional

embedding space. Images belong to different classes (i. e. _l__i_ ≠ _l__j_) will be farther apart in the low dimensional embedding space. Images where class information is unknown (i.e.

_l__i_ or _l__j_ are undefined) will be near images determined to be similar, in terms of ϕ(·, ·), regardless of class. OUT-OF-SAMPLE EXTRAPOLATION (OSE) OSE uses Y determined from C to

extrapolate _y__q_ for . Assuming that Y accurately describes the non-linear relationships in C, which should be the case when C is sufficiently large, OSE is able to accurately determine

_y__q_38,39. OSE is divided into three steps, * 1 Manifold Learning: A set of low dimensional embeddings Y are learned by performing GE on C as described in the Graph Embedding Section. * 2

Query Image Descriptor Calculation: Pairwise dissimilarity _A_(_i, q_) is calculated between and every image contained in C. _W_(_i, q_) is calculated from _A_(_i, q_). * 3 Query Sample

Extrapolation: The embedding location _y__q_ for is extrapolated via, where _k_ ∈ {1, …, _d_} is the _k_th embedding dimension corresponding to the _k_th smallest eigenvalue λ_k_.

Intuitively, OSE calculates _y__q_ as a weighted sum of the database embeddings _y__i_: _i_ ∈ {1, …, _N_} where weights are based on image similarity described by _W_(_i, q_). OUT-OF-SAMPLE

EXTRAPOLATION FOR SEMI-SUPERVISED MANIFOLD LEARNING OSE-SSL is a novel combination of the previously described SSL and OSE algorithms that projects never-before seen images into a low

dimensional embedding space that incorporates semantic information. OSE-SSL calculates Y_r_ for C such that (a) the image class labels L_r_ are taken into account and (b) image similarity is

optimally represented by Y_r_. After Y_r_ have been calculated for C, a new never before seen image can be extrapolated into the low dimensional space to obtain Y_q_. OSE-SSL calculates the

embedding Y_q_ in a computationally efficient manner. Our novel methodology for OSE-SSL can be divided into an offline _ConstructOSE-SSL_ algorithm and an online _ApplyOSE-SSL_ algorithm

both of which are described in detail below. OSE-SSL ALGORITHM The algorithm for OSE-SSL is divided into two parts, (1) _ConstructOSE-SSL_ which is an offline computationally intensive

algorithm to learn Y_r_ that only needs to be performed once for C and (2) _ApplyOSE-SSL_ which is an online algorithm to extrapolate _y__q_ for . The combination of these two algorithms

results in a low dimensional representation for both C and . The _ConstructOSE-SSL_ algorithm takes into account only images contained in the database C and the corresponding semantic

information L_r_. The algorithm is as follows, ALGORITHM _ConstructOSE-SSL_ INPUT: C, L_r_ OUTPUT: λ_r_, Y_r_ _begin_ * 1 Find , _j_ ∈ {1, …, _N_}. * 2 Find _W__r_ by Equation 3. * 3 Find

λ_r_, Y_r_ by Equation 2. _end_ As with other SSL algorithms the use of labels L_r_ alters the similarity matrix _W__r_ so that images belonging to the same class are more similar. The

structure of _W__r_ is changed such that _W__r_ can be approximated as a block matrix where each block consists of samples belonging to the same class. An approximate block matrix

formulation results in the EVD producing Y_r_ that are more representative of the class differences that exist in the database C. Once the eigenvalues λ_r_ and the embedding locations Y_r_

have been computed, extrapolation of into the low dimensional embedding space can be performed via the _ApplyOSE-SSL_ algorithm, ALGORITHM _ApplyOSE-SSL_ INPUT: _C__q_, λ_r_, Y_r_ OUTPUT:

_y__q_ _begin_ * 1 Find for all _i_ ∈ {1, …, _N_}. * 2 Calculate _W_(_i, q_) = _e_−_A_(_i_,_q_)/σ. * 3 Find _y__q_ by Equation 4. _end_ These two algorithms in combination allow for a low

dimensional embedding space to be found for C and . The use of Y_r_ which are more reflective of the underlying class differences in C to calculate _y__q_ provides two benefits. Firstly,

_y__q_ will capture more information pertaining to class differences in C when using Y_r_ compared to the unsupervised embeddings Y. Secondly, tthe error between _y__q_ and its true location

(determined by performing an EVD) will be smaller when calculated from Y_r_ that contain relevant class differences in C. APPLICATION TO IMAGE RETRIEVAL The goal of a CBIR system is to

retrieve _b_ images in C which are most similar to . The application of OSE-SSL to a CBIR system can be applied to learn the metric where is defined such that smaller values correspond to

more similar images. Offline database construction is an important precursor to image retrieval and is performed using the algorithm _ConstructOSE-SSL_. Online retrieval of the most similar

images in C is performed by the algorithm _RetrieveOSE-SSL_ as follows, ALGORITHM _RetrieveOSE-SSL_ INPUT: _C__q_, Y_r_ OUTPUT: _begin_ * 1 Extrapolation of _y__q_ for via _ApplyOSE-SSL_. *

2 Calculation of similarity between C and by, * 3 Sort from smallest to largest value to give S. * 4 Return corresponding to the smallest _b_ values in S. _end_ OSE-SSL COMPUTATIONAL

COMPLEXITY To analyze the computational complexity of our novel OSE-SSL algorithm we consider _ConstructOSE-SSL_ and _ApplyOSE-SSL_ separately. _ConstructOSE-SSL_ is a SSL algorithm applied

to C. SSL has a computational complexity of _O_(_N_3) due to the EVD in Equation 2 which is the rate limiting step40. However as _ConstructOSE-SSL_ is utilized only to learn a low

dimensional representation of C it is performed offline prior to image retrieval. _ApplyOSE-SSL_ learns _y__q_ for and hence must be performed online. The computational complexity of OSE is

_O_(_N_) due to the weighted summation in Equation 4 40. EXPERIMENTAL DESIGN AND RESULTS We evaluated our _RetrieveOSE-SSL_ algorithm on a prostate histpathology dataset described below.

This dataset demonstrates the application of _RetrieveOSE-SSL_ in retrieving images by Gleason grade using gland morphology. All code was implemented in MatLab® 2012b and run on a computer

with a 3.0 GHz Xeon Quad-Core processor and 16 GB of RAM. PROSTATE HISTOPATHOLOGY DATA DESCRIPTION Prostate tissue biopsy cores were obtained from 58 patient studies. Each tissue biopsy was

stained with Hemotoxylin and Eosin (H&E) and digitized using a ScanScope CSTM whole-slide scanning system at 0.25 _μm_ per pixel (40× optical magnification). An expert pathologist

selected regions of interests (ROIs) on the digitized biopsy image, for a total of 102 ROIs. The expert pathologist then classified each ROI as benign (BE) (24 ROIs), Gleason grade 3 (G3)

(67 ROIs), or Gleason grade 4 (G4) (11 ROIs). Every gland contained within each ROI was segmented by a human expert to obtain lumen and nuclear boundaries, the human expert was blinded to

the Gleason grade for all glands. Glands which did not contain either a nuclear or lumen boundary, or where the contour was not fully contained within the ROI were removed from the study,

resulting in a total of 888 glands. Glands were distributed across the three classes: BE (93), G3 (748) and G4 (47). Dissimilarity between prostate histopathology images is determined

according to morphologic similarity between prostate glands on each image. The function is calculated by leveraging ESDs, a method previously developed by our group8. DATABASE CONSTRUCTION

For the dataset a query image was selected such that each image in the dataset was selected once. C was constructed by randomly selecting _N_ images, where _N_ was empirically determined,

from the dataset in such a way as to always maintain class balance. Class balance was maintained by always selecting the same ratio of each class of images, i.e. constructing C via

stratified sampling of the dataset images. Additionally, the query image was always excluded from C. Construction of L_r_ was performed by randomly selecting _M_ labels, where _M_ was

empirically determined, from the images in C in such a way as to maintain class balance. Additionally for all experiments _M_ ≤ _N_, so that the total number of known labels were always less

than or equal to _N_. The OSE-SSL algorithm has two important empirically determined parameters, dataset size _N_ and number of known labels _M_. To enable direct comparison between _N_ and

_M_ these parameters are evaluated as a fraction of the dataset size. Specifically, we define a parameter _n_ is a value between 0 and 1 such that _N_ = _n_ × _N__all_. Hence _n_ = 0.5

indicates that half of the total dataset available is being used to construct C. Similarly, _m_ is defined to be a value between 0 and _l_ such that _M_ = _m_ × _N_. Hence, _m_ = 0.5

represents half of the labels in the database C being known. EVALUATION MEASURES OSE-SSL was evaluated on (a) Silhouette Index (SI) of Y, a measure of how well images cluster according to

class41 and (b) area under the precision-recall curve (AUPRC) of _RetrieveOSE-SSL_, a description of the behavior of an image retrieval system in terms of how many and in what order relevant

images are returned. Table 3 describes all evaluation measures. EXPERIMENT 1: DISTANCE METRIC FOR PROSTATE HISTOPATHOLOGY DATABASE In this experiment we evaluated the ability of to retrieve

relevant images for the prostate histopathology dataset. Five other distance metrics discussed in Table 4 were used for comparison. is a special case of where is contained in C (equivalent

to _m_ = 0.0 and _n_ = 1.0), hence, _y__q_ is calculated using Equation 2 for GE and is a non-linear unsupervised feature space. Distance metrics were chosen in order to evaluate the

original feature space , a linear unsupervised feature space , a linear approximation of an unsupervised non-linear feature space and a non-linear semi-supervised feature space that uses

kernel-based hashing . For and some labels are known (_m_ = 0.5) and not all images are contained in the database (_n_ = 0.9). For not all images are contained in the database (_n_ = 0.9).

The number of dimensions for , , and as well as the scaling parameter σ corresponding to the best retrieval performance were determined empirically and are reported in Table 5. Parameters

for were determined as described in42. AUPRC and SI were calculated on a set of query images such that each image in the dataset was selected once. In Table 5 we report SI and AUPRC average

value ± standard deviation over all 888 query images in the prostate histopathology databse for each distance metric. Figure 3 displays the AUPRC curves for each distance metric. performs

better retrieval, in terms of higher AUPRC and SI compared to either or . These differences were found to be statistically significant (_p_ < 0.05) using a paired two-sided Student’s

t-test where the null hypothesis was that the performance of was not different compared to another distant metric (, , or ). Additionally, increases in SI and AUPRC for (_n_ = 0.9, _m_ = 

0.5) compared to was found to be statistically significant. Figure 4 displays the top 5 retrieved images for a G4 gland query image. (_n_ = 0.9, _m_ = 0.5) was able to retrieve only glands

belonging to the same class as . retrieved some glands incorrectly, probably due to the retrieved BE and G3 glands being atypical in shape and size for their class. The use of class

information to learn the embeddings most likely allowed to learn a greater range of morphology traits for each class. was unable to retrieve any glands belonging to the same class. The

failure to retrieve G4 glands is most likely due to only capturing the main characteristics of the query gland, being small and roughly circular, while failing to capture the subtle

undulations in the gland boundary that is a distinguishing feature between G3 and G4 glands. Figure 5 shows the top 5 retrieved images for a G3 gland query image. (_n_ = 0.9, _m_ = 0.5) was

able to retrieve only glands belonging to the same class as . All of these images were of small, elongated glands. Both and retrieved the same BE glands mistakenly in addition to G3 glands.

The BE glands are elongated but slightly larger and having different patterns in terms of boundary perturbations. Figure 6 displays a particularly hard to classify of a BE gland and the

corresponding top 5 images retrieved. Further evaluation of this gland showed that due to its small size compared to other BE glands, Φ(·, ·) often resulted in a higher than expected

dissimilarity between this gland and other BE glands, resulting in retrieving glands belonging to other classes. did not retrieve any glands belonging to the same class in this example.

embeddings did note to capture subtle gland features, the gland size and the boundary undulations, that distinguish BE glands from other grades. and were able to retrieve glands belonging to

the same class. However, ranked glands belonging to the same class higher compared to . For both and , glands retrieved from different classes were likely to have subtle differences in the

nuclear and lumen boundary attributes, cues that were not captured by any embedding space. EXPERIMENT 2: PARAMETER SENSITIVITY In this experiment we evaluated the ability of to retrieve

relevant images for the prostate histopathology dataset under for a range of parameter conditions. For there are two parameters which may be selected by the user, _N_ the number of images

contained in C and _M_ the number of labels known for C. Parameters _M_ and _N_ were evaluated independently by holding the parameter not under consideration constant. The defaults for the

parameter not under consideration were _n_ = 1.0 and _m_ = 0.0, as already mentioned when _n_ = 1.0 and _m_ = 0.0 the distance metrics and are equivalent. The parameters _M_ and _N_ were

also evaluated together to explore the synergistic effects of _M_ and _N_ on image retrieval. EFFECT OF KNOWN LABEL SIZE (_M_) We hypothesized that adding label information via SSL would

improve the ability of the low dimensional embedding space to distinguish between images belonging to different classes. Figure 7 displays the SI and AUPRC values of the baseline case of no

labels (pink) and SSL by varying the number of known labels (light blue). Adding label information improved SI and AUPRC for large _M_. EFFECT OF DATABASE SIZE (_N_) We hypothesized for

OSE-SSL small _N_ would be unable to uncover the underlying structure in the database and result in embeddings which are less than optimal. As shown in Fig. 8, for _n_ < 0.9 OSE was

unable to accurately extrapolate embeddings. However, for _n_ ≥ 0.9 there are no statistically significant differences (p-value > 0.05) between embeddings found via OSE and recomputing

the EVD of the similarity matrix (i.e. embeddings found via GE). RELATIONSHIP BETWEEN DATABASE SIZE (_N_) AND KNOWN LABEL SIZE (_M_) The relationships between the SSL and OSE components of

the OSE-SSL were evaluated. Increasing the known labels (_M_) necessitates a concomitant increase in database size (_N_) to appropriately model the embedding space. This trend is shown in

Fig. 9 where for _m_ = 0.0 a training set size of _n_ = 0.9 is able to appropriately extrapolate embeddings. However, when _m_ = 0.85 a training set size of _n_ = 1.0 is required to

appropriately extrapolate embeddings (i.e. GE must be utilized to learn the embeddings). In this database, _N_ is not sufficiently high to capture the underlying structure if _M_ is

increased. Despite not having a large enough _N_ to capture the underlying image structure increasing _M_ does result in better AUPRC and SI measures even for small _N_. EXPERIMENT 3:

COMPUTATIONAL TIME In this experiment we evaluated the time to retrieve images used the three distance metrics: , and to retrieve relevant images for the prostate histopathology dataset

using a range of training database sizes (_N_) and number of query images (_Q_). As shown in Fig. 10 and are able to retrieve images most similar to a query in approximately the same amount

of time while requires more time to perform an equivalent retrieval. Figure 10(c) displays under what conditions the time increases in retrieval for are statistically significant (red). For

larger _N_ and larger _Q_, takes a statistically significant amount of time longer, the higher the values for _N_ and _Q_ the more pronounced this effect is. The increase in time for is due

to two factors (a) requires more pairwise comparisons between and the images contained in C and (b) requires a computationally expensive EVD to compute _y__q_, the low dimensional embedding

for the query image. DISCUSSION In this paper we have presented a novel combination out-of-sample extrapolation with semi-supervised manifold learning (OSE-SSL) that first refines

relationships between images in the low dimensional embedding space according to semantic information via SSL and then utilizes OSE to project never before seen images into the low

dimensional space learned via SSL. We have demonstrated the application of OSE-SSL for content-based image retrieval (CBIR) of prostate histpathology. Image similarity within our CBIR

framework is defined using Explicit Shape Descriptors (ESDs), ESDs were previously developed by our group to classify Gleason grade on prostate histopathology according to gland morphology8.

In this work we leverage the accurate ESDs to determine similarity between images and then apply the OSE-SSL algorithm to retrieve images which are most similar in a computationally

efficient manner. CBIR for histopathology, has as histopathology images require many image descriptors to accurately describe the large amounts of complex data present. Retrieval directly

within the high dimensional feature space for histopathology images is difficult, as demonstrated by the relatively poor retrieval rates in the original high dimensional feature space and

using linear DR approaches . Manifold learning (ML) can be leveraged to find a low dimensional representation where image similarity calculation and retrieval can be performed accurately and

efficiently. In this paper we demonstrated that ML is able to retrieve histopathology images accurately, which has very limited previous work6,7 Our OSE-SSL CBIR algorithm was evaluated for

a prostate histopathology database containing 888 glands. OSE-SSL outperformed image retrieval in the high dimensional space as well as in a low dimension space found by Principal Component

Analysis (PCA) (as described in Experiment 1). We demonstrated that OSE-SSL was able to accurately retrieve images utilized a low dimensional embedding space found via SSL on a training

database that was smaller compared to the full dataset. For the prostate histopathology dataset _M_ = 0.85 of the dataset, or 754 images, was required to achieve retrieval rates comparable

to those achieved by performing an EVD for each new query image. Finally, incorporating known label information was able to improve retrieval rates. The current work is limited in that CBIR

was performed on a per patch basis, where multiple patches are defined over a single slide. However, pathologists typically utilize the whole slide to determine Gleason grade pattern.

Additionally, in this work we have leveraged only gland morphology to determine similarity between image patches. However, pathologists typically evaluate Gleason grade using the morphology

and arrangement of glands and nuclei2. Future work will involve incorporating our gland based retrieval into a whole slide similarity metric, which will be capable of retrieving whole slides

which contain similar image characteristics, likely including measures of nuclei arrangement43 and nuclei morphology44. The current work is also limited by the fact that all 58 patients had

prostate tissue biopsy cores acquired at a single institution. Therefore, the dataset used in this work may be more homogeneous, in terms of tissue staining and digitization of the slides,

compared to a dataset of prostate histopathology images acquired across several institutions. While these differences between institutions will likely affect pre-processing steps such as

automated segmentation, in this work we have limited the effects of a homogeneous dataset by relying on manual segmentation. The variability in gland morphology is independent of

institution, as gland morphology is a function of disease grade. Future work will evaluate the presented methodology on a larger patient cohort acquired across institutions. Additionally,

the current work only evaluated morphologic features (ESDs) of glands present on prostate histopathology. Previous work has shown that texture6,7 and nuclear architecture6,7,11 are also able

to provide accurate image retrieval of prostate histopathology. The OSE-SSL algorithm is not limited to ESDs, hence, alternative dissimilarity measures that combine ESDs with other features

derived from the prostate histopathology images can be implemented within our CBIR framework. Future work will evaluate the dissimilarity measures that combine multiple image features.

ADDITIONAL INFORMATION HOW TO CITE THIS ARTICLE: Sparks, R. and Madabhushi, A. Out-of-Sample Extrapolation utilizing Semi-Supervised Manifold Learning (OSE-SSL): Content Based Image

Retrieval for Histopathology Images. _Sci. Rep._ 6, 27306; doi: 10.1038/srep27306 (2016). REFERENCES * Siegel, R., Naishadham, D. & Jemal, A. Cancer statistics. CA: A Cancer Journal for

Clinicians 62, 10–29 (2012). Google Scholar  * Epstein, J. I., Allsbrook, W. C., Amin, M. B. & Egevad, L. L. The 2005 international society of urological pathology (ISUP) consensus

conference on Gleason grading of prostatic carcinoma. Am. J. Surg. Pathol. 29, 1228–1242 (2005). Article  Google Scholar  * Epstein, J. I. An update of the gleason grading system. The

Journal of Urology 183, 433–440 (2010). Article  Google Scholar  * Madabhushi, A., Agner, S., Basavanhally, A., Doyle, S. & Lee, G. Computer-aided prognosis: Predicting patient and

disease outcome via quantitative fusion of multi-scale, multi-modal data. Computerized Medical Imaging and Graphics 35, 506–514 (2011). Article  Google Scholar  * Allsbrook, W. C. et al.

Interobserver reproducibility of Gleason grading of prostatic carcinoma: General pathologist. Human Pathology 32, 81–88 (2001). Article  Google Scholar  * Doyle, S. et al. Using manifold

learning for content-based image retrieval of prostate histopathology. In _Workshop on Content-Based Image Retrieval for Biomedical Image Archives (in conjunction with MICCAI_) 53–62 (2007).

* Naik, S. et al. A boosted distance metric: Application to content based image retrieval and classification of digitized histopathology. In Proc. SPIE vol. 7260, 72603F (2009). Article 

Google Scholar  * Sparks, R. & Madabhushi, A. Explicit shape descriptors: Novel morphologic features for histopathology classification. Medical Image Analysis 17, 997–1009 (2013).

Article  Google Scholar  * Zheng, L., Wetzel, A. W., Gilbertson, J. & Becich, M. J. Design and analysis of a content-based pathology image retrieval system. Information Technology in

Biomedicine, IEEE Transactions on 7, 249–255 (2003). Article  Google Scholar  * Comaniciu, D., Meer, P. & Foran, D. Image-guided decision support system for pathology. Machine Vision and

Applications 11, 213–224 (1999). Article  Google Scholar  * Wetzel, A. W. et al. Evaluation of prostate tumor grades by content-based image retrieval vol. 3584, 244–252 (SPIE, 1999). Google

Scholar  * Tang, H. L., Hanka, R. & Ip, H. H. S. Histological image retrieval based on semantic content analysis. Information Technology in Biomedicine, IEEE Transactions on 7, 26–36

(2003). Article  Google Scholar  * Lessmann, B., Nattkemper, T. W., Hans, V. H. & Degenhard, A. A method for linking computed image features to histological semantics in neuropathology.

Journal of Biomedical Informatics 40, 631–641 (2007). Article  CAS  Google Scholar  * Yu, F. & Ip, H. H. S. Semantic content analysis and annotation of histological images. Computers in

Biology and Medicine 38, 635–649 (2008). Article  Google Scholar  * Yang, L. et al. Pathminer: a web-based tool for computer-assisted diagnostics in pathology. Trans. Info. Tech. Biomed. 13,

291–299 (2009). Article  Google Scholar  * Caicedo, J. C., González, F. A. & Romero, E. Content-based histopathology image retrieval using a kernel-based semantic annotation framework.

Journal of Biomedical Informatics 44, 519–528 (2011). Article  Google Scholar  * Madabhushi, A. Digital pathology image analysis: Oppurtunities and challenges. Imaging in Medicine 1, 7–10

(2009). Article  Google Scholar  * Bellman, R. Curse of dimensionality. Adaptive control processes: a guided tour. Princeton, NJ (1961). * Lee, G., Rodriguez, C. & Madabhushi, A.

Investigating the efficacy of nonlinear dimensionality reduction schemes in classifying gene and protein expression studies. IEEE/ACM Transactions on Computational Biology and Bioinformatics

5, 368–384 (2008). Article  CAS  Google Scholar  * He, J., Li, M., Zhang, H., Tong, H. & Zhang, C. Generalized manifold-ranking-based image retrieval. IEEE Transactions on Image

Processing 15, 3170–3177 (2006). Article  ADS  Google Scholar  * El-Naqa, I., Yang, Y., Galatsanos, N. P., Nishikawa, R. M. & Wernick, M. N. A similarity learning approach to

content-based image retrieval: application to digital mammography. Medical Imaging, IEEE Transactions on 23, 1233–1244 (2004). Article  Google Scholar  * Bian, W. & Tao, D. Biased

discriminant euclidean embedding for content-based image retrieval. IEEE Transactions on Image Processing 19, 545–554 (2010). Article  ADS  MathSciNet  Google Scholar  * Shi, J. & Malik,

J. Normalized cuts and image segmentation. IEEE Transactions on Pattern Analysis and Machine Learning 22, 888–905 (2000). Article  Google Scholar  * Roweis, S. & Saul, L. Nonlinear

dimensionality reduction by locally linear embedding. Science 290, 2323–2326 (2000). Article  CAS  ADS  Google Scholar  * Tenenbaum, J., de Silvia, V. & Langford, J. A global framework

for nonlinear dimensionality reduction. Science 290, 2319–2323 (2000). Article  CAS  ADS  Google Scholar  * Zhao, H. Combining labeled and unlabeled data with graph embedding. Neurocomputing

69, 2385–2389 (2006). Article  Google Scholar  * He, X. Laplacian regularized d-optimal design for active learning and its application to image retrieval. IEEE Transactions on Image

Processing 19, 254–262 (2010). Article  ADS  MathSciNet  Google Scholar  * He, X. & Niyogi, P. Locality preserving projections. In Advances in Neural Information Processing Systems 16,

153–160 (2004). Google Scholar  * Bengio, Y. et al. Out-of-Sample Extensions for LLE, Isomap, MDS, Eigenmaps and Spectral Clustering. In In Advances in Neural Information Processing Systems

16, 177–184 (2004). Google Scholar  * Shyu, C.-R. et al. Assert: A physician-in-the-loop content-based retrieval system for hrct image databases. Computer Vision and Image Understanding 75,

111–132 (1999). Article  Google Scholar  * Caicedo, J. C., Vanegas, J. A., Páez, F. & González, F. A. Histology image search using multimodal fusion. Journal of Biomedical Informatics

51, 114–128 (2014). Article  Google Scholar  * Zhang, Q. & Izquierdo, E. Histology image retrieval in optimized multifeature spaces. IEEE Journal of Biomedical and Health Informatics 17,

240–249 (2013). Article  Google Scholar  * Zhang, X., Liu, W. & Zhang, S. Mining histopathological images via hashing-based scalable image retrieval. In _Biomedical Imaging (ISBI_),

_2014 IEEE 11th International Symposium on_, 1111–1114, doi: 10.1109/ISBI.2014.6868069 (2014). * Jiang, M., Zhang, S., Huang, J., Yang, L. & Metaxas, D. N. _Medical Image Computing and

Computer-Assisted Intervention_–_MICCAI 2015: 18th International Conference, Munich, Germany, October_ 5–9, 2015, _Proceedings, Part III_, chap. Joint Kernel-Based Supervised Hashing for

Scalable Histopathological Image Analysis, 366–373 (Springer International Publishing, 2015). * Zhang, X., Liu, W., Dundar, M., Badve, S. & Zhang, S. Towards large-scale

histopathological image analysis: Hashing-based image retrieval. IEEE Transactions on Medical Imaging 34, 496–506 (2015). Article  Google Scholar  * Zhang, X., Xing, F., Su, H., Yang, L.

& Zhang, S. High-throughput histopathological image analysis via robust cell segmentation and hashing. Medical Image Analysis 26, 306–315 (2015). Article  Google Scholar  * Belkin, M.

& Niyogi, P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Computation 15, 1373–1396 (2003). Article  Google Scholar  * Fowlkes, C., Belongie, S.,

Chung, F. & Malik, J. Spectral grouping using the Nyström method. IEEE TPAMI 28, 214–225 (2004). Article  Google Scholar  * Ouimet, M. & Bengio, Y. Greedy spectral embedding. In

Proceedings of the Tenth International Workshop on Artificial Intelligence and Statistics Barbados, New Jersey, USA: The Society for Artificial Intelligence and Statistics (Jan. 6, 2005). *

Zhang, K. & Kwok, J. T. Density-weighted Nyström method for computing large kernel eigensystems. Neural Computation 21, 121–146 (2009). Article  MathSciNet  Google Scholar  * Rousseeuw,

P. Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. Journal of Computational Applied Mathematics 20, 53–65 (1987). Article  Google Scholar  * Liu, W.,

Wang, J., Ji, R., Jiang, Y.-G. & Chang, S.-F. Supervised hashing with kernels. In _Computer Vision and Pattern Recognition (CVPR_), _2012 IEEE Conference on_, 2074–2081, doi:

10.1109/CVPR.2012.6247912 (2012). * Doyle, S., Feldman, M., Tomaszewski, J. & Madabhushi, A. A boosted bayesian multi-resolution classifier for prostate cancer detection from digitized

needle biopsies. IEEE Transactions on Biomedical Engineering 59, 1205–1218 (2012). Article  Google Scholar  * Ali, S. & Madabhushi, A. An integrated region-, boundary-, shape-based

active contour for multiple object overlap resolution in histological imagery. Medical Imaging, IEEE Transactions on 31, 1448–1460 (2012). Article  Google Scholar  Download references

ACKNOWLEDGEMENTS Research reported in this publication was supported by the National Cancer Institute of the National Institutes of Health under award numbers 1U24CA199374-01,

R21CA167811-01, R21CA179327-01, R21CA195152-01; the National Institute of Diabetes and Digestive and Kidney Diseases under award number R01DK098503-02; the DOD Prostate Cancer Synergistic

Idea Development Award (PC120857); the DOD Lung Cancer Idea Development New Investigator Award (LC130463); the DOD Prostate Cancer Idea Development Award; the Ohio Third Frontier Technology

development Grant, the CTSC Coulter Annual Pilot Grant, the Case Comprehensive Cancer Center Pilot Grant VelaSano Grant from the Cleveland Clinic the Wallace H. Coulter Foundation Program in

the Department of Biomedical Engineering at Case Western Reserve University. The content is solely the responsibility of the authors and does not necessarily represent the official views of

the National Institutes of Health. We would like to thank Dr. J.E. Tomaszewski from the School of Medicine at the State University of New York, Buffalo as well as Drs. M.D. Feldman and N.

Shih from the Hospital of the University of Pennsylvania for providing prostate histology imagery and corresponding annotations. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * University

College of London, Centre for Medical Image Computing, London, UK Rachel Sparks * Department of Biomedical Engineering, Case Western Reserve University, Cleveland, OH, USA Anant Madabhushi

Authors * Rachel Sparks View author publications You can also search for this author inPubMed Google Scholar * Anant Madabhushi View author publications You can also search for this author

inPubMed Google Scholar CONTRIBUTIONS R.S. and A.M. conceived the experiments and methodology. R.S. conducted the experiments and analyzed the results. All authors reviewed the manuscript.

ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing financial interests. RIGHTS AND PERMISSIONS This work is licensed under a Creative Commons Attribution 4.0

International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the

material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit

http://creativecommons.org/licenses/by/4.0/ Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Sparks, R., Madabhushi, A. Out-of-Sample Extrapolation utilizing Semi-Supervised

Manifold Learning (OSE-SSL): Content Based Image Retrieval for Histopathology Images. _Sci Rep_ 6, 27306 (2016). https://doi.org/10.1038/srep27306 Download citation * Received: 17 December

2015 * Accepted: 16 May 2016 * Published: 06 June 2016 * DOI: https://doi.org/10.1038/srep27306 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content:

Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative