The impact of faulting complexity and type on earthquake rupture dynamics

ABSTRACT The statistical properties of seismicity are known to be affected by several factors such as the rheological parameters of rocks. We analysed the earthquake double-couple as a

function of the faulting type. Here we show that it impacts the moment tensors of earthquakes: thrust-faulting events are characterized by higher double-couple components with respect to

strike-slip- and normal-faulting earthquakes. Our results are coherent with the stress dependence of the scaling exponent of the Gutenberg-Richter law, which is anticorrelated to the

double-couple. We suggest that the structural and tectonic control of seismicity may have its origin in the complexity of the seismogenic source marked by the width of the cataclastic damage

zone and by the slip of different fault planes during the same seismic event; the sharper and concentrated the slip as along faults, the higher the double-couple. This phenomenon may

introduce bias in magnitude estimation, with possible impact on seismic forecasting. SIMILAR CONTENT BEING VIEWED BY OTHERS STRESS LOADING HISTORY OF EARTHQUAKE FAULTS INFLUENCED BY

FAULT/SHEAR ZONE GEOMETRY AND COULOMB PRE-STRESS Article Open access 29 July 2020 INTEGRATED RUPTURE MECHANICS FOR SLOW SLIP EVENTS AND EARTHQUAKES Article Open access 28 November 2022

IRREGULAR RUPTURE PROPAGATION AND GEOMETRIC FAULT COMPLEXITIES DURING THE 2010 MW 7.2 EL MAYOR-CUCAPAH EARTHQUAKE Article Open access 17 March 2022 INTRODUCTION Earthquakes contribute to

dissipating the energy accumulated in the brittle lithosphere due to the tectonic stress arising from the motion of contiguous crustal volumes with respect to each other. Thrust faulting,

usually featured by angles of dip ranging in between 5°−30°, mostly occurs along the margins of plates, where their motions induce elastic strain accumulation, which is released by

multifaceted fault slip dynamics ranging from almost periodic silent events to megathrust earthquakes1. Strike-slip-faulting earthquakes are localized along steeply dipping faults (70°−90°)

or transcurrent plate boundaries and transfer zones, while normal faults develop along rift zones in extensional regimes having intermediate dip (45°−65°). Structural, morphological, and

geophysical differences have been highlighted among the three main tectonic settings2,3,4. Normal faults cause fracturing mainly concentrated in the hanging walls and spaced clusters of

parallel faults across rifting areas5,6,7. Intricated geometries are also typical of transcurrent regions, often accompanied by releasing and restraining bends or step-overs and other

geological structures shedding light on complex spatial stress patterns8,9; experiments in the lab support geological observations10. Conversely, thrust-faulting earthquakes usually occur

along gently dipping subductions characterized by a unique, longitudinally extended front which slip is localized at11,12. The dynamics of fluids has been also noticed to vary with the

faulting type13. In extensional tectonics, fluids percolate into fractures during the interseismic period, whereas they are expelled during the coseismic phase, while the opposite is

observed in compressive geodynamic settings14,15. Such a fan of geological manifestations also mirrors a seismological counterpart16: normal fault earthquakes are featured by a steeper

power-law frequency-size distribution than transcurrent and reverse seismicity respectively17,18,19, with lower cut-off magnitudes20 and higher fractal dimension of the hypocenters’ time

series of aftershocks21,22. The latter property clearly states that the post-seismic relaxation is spread over several fault patches. Recently, sound evidence has been provided that fault

structure plays a key role in driving almost all the crucial large-scale processes characterizing seismic dynamics23 such as the localization of earthquake nucleation, propagation and arrest

of rupture and aftershock occurrence. The rheological properties of fault rocks are related to the dynamics of coseismic slip, which, in turn, is connected to the topological features of

faulting. The roughness of the dislocation surface is proven to affect stress accumulation, strain accommodation and release24. In this regard, geometrical complexities, and heterogeneity,

i.e., state of fracturing and fault topology, represent the hidden factor shaping the seismic dynamics from coseismic to spatial and temporal scale of tectonics25,26,27. Fault topology is in

fact suggested to control the statistical properties of seismicity, producing a wide range of behaviors with different varying recurrence times, periodicity, and consistency over time in

seismic time series, its magnitude and radiation pattern28. The moment tensor is the most complete quantitative information that can be extracted from seismic recordings29. The moment tensor

is symmetric with six independent components. It can be decomposed into an isotropic part (ISO), a double-couple (DC) and a compensated linear vector dipole (CLVD). The isotropic part

provides a measure of the volume change, while the deviatoric contribution, i.e., the second and the third terms, have null trace. In the simplest case, an earthquake can be thought as a

unidirectional slip on a single fault plane, so that its moment tensor can be represented by a double-couple of forces acting with null net torque30. However, real faults are not planar

surfaces, nor have they well-defined simple geometries at all. They are fractals31,32,33 which stem from spatial self-organization. Hence, large-scale heterogeneities34, not only friction,

are likely to control the development of fault systems producing complex ruptures which can lead to low DC components in the moment tensors35. Non-DC events can have different physical

origins: high ISO terms are usually caused by varying fluid flow, landslides, and volcanic eruptions; explosions are classical examples of artificial ISO-earthquakes. Non-planar or

multi-patch ruptures are instead characterized by significant CLVD components, e.g.36,37. They arise from the sum of DC-like moment tensors produced by shear faulting on locally planar

fractures with different spatial orientations38. Other possible origins are shear fractures in heterogeneous and anisotropic media (e.g., facies transitions). Therefore, the CLVD

contribution can be considered a suggestive marker for topological complexity of the seismic source and thus, moment tensors may be suitable to delve into the dynamics of the coseismic

fracture. Nevertheless, above all for shallow seismic events, some moment tensor components may not be accurately determined, producing spurious non-DC39. Wrong hypocentre localizations,

centroid mis-location, and inaccurate velocity models of seismic waves in the crust and in the mantle can also be responsible for spurious non-DC moment tensors40. For these reasons, non-DC

components have been considered to be artifacts in most of the cases41,42. The previous conclusion was also supported by the large scatter of data and errors in different catalogues43

suggesting that better detection procedures should be required before a minimal accuracy could be get for a reliable analysis of CLVDs. Nowadays, much larger and detailed moment tensor

catalogues are available than in the past, which allow us to perform a new analysis. RESULTS The statistical analysis of two global catalogues44,45,46,47 of moment tensors clearly shows that

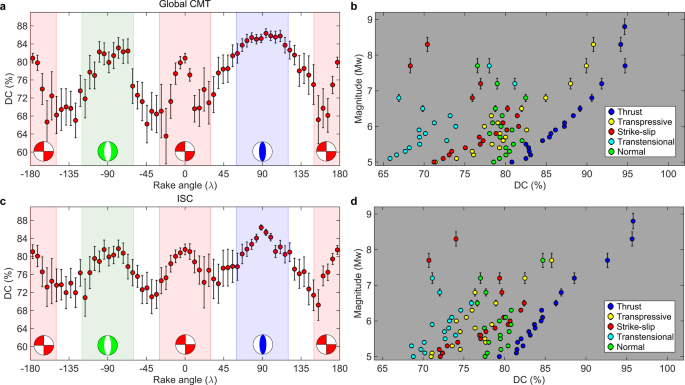
the DC contributions are not uniformly distributed as a function of the angle of rake. The type of event is classified according to the Aki-Richards convention29: an earthquake is a

“thrust-faulting event” if its rake is in the range 90° ± 30°, while normal-faulting earthquakes fall in −90° ± 30° and strike-slip events are in 0° ± 30°, ±180° ∓ 30°. Thrust-faulting

events are characterized by higher DC values, as already reported in42, followed by normal, transpressive and strike-slip ones respectively. Transtensional tectonic settings host seismicity

featured by the largest CLVD contribution (Fig. 1a, c). Data confirms the statistical significance of the variability in the composition of moment tensors in different faulting types (Table 

1) also in regional moment tensor catalogues48,49, even though with less evident outputs, likely because of asymmetric statistics of focal mechanisms (e.g., the NIED database mostly lists

reverse fault earthquakes and only few normal-faulting ones). Different behaviours are also observed regarding the correlation between CLVD values and the size of earthquakes. A clear

increase of the DC with the magnitude is measured for compressive and transpressive data sets, while the size of normal and transtensional events do not seem to affect their non-DC

components. Transcurrent seismicity displays a positive correlation at moderate magnitudes while it turns negative at larger (> 6) ones (Fig. 1b, d). The average DC contributions are

found to be positively correlated with the magnitude of the largest event in the catalogue (Fig. 2a, c), i.e., the corner magnitude of the frequency size-distribution, and negatively

correlated with the b-value of the Gutenberg-Richter law (Fig. 2b, d). This output is coherent with the DC distribution as a function of the rake angle and with its correlation with the size

of earthquakes. Our results for the Global CMT and the ISC reviewed catalogues are compatible with each other. A plot of the normalized frequency of the rake angle as a function of the DC

clarifies that the differences in the mean DC values in Table 1 are only partially produced by displaced statistical modes, while the misfit is mostly due to larger high-order moments of the

distributions. Thrust earthquakes are usually featured by elevated plane shear components of the moment tensors with limited dispersion. The variance of the distribution increases for

normal and strike-slip earthquakes. It reaches its maximum value in the case of transtensional seismicity, whose distribution is markedly spread over a large interval (Fig. 3a). At last, the

geographical localization of seismic events as a function of their moment tensor contents seems to be not spatially homogeneous (Fig. 3b): non-DC earthquakes more likely occur along

transfer zones, intra-plate settings and slow deforming continental regions. Differently, almost pure DC events are clustered along the subduction zones. This qualitative observation is also

coherent with previous results. While the first part of our analysis is focused on shallow seismicity (hypocentral depth lower than 50 km), we also investigate how the composition of moment

tensors is affected by depth (Fig. 4). Our results show that the DC components tend to be more and more uniform as a function of the angle of rake increasing depth. DISCUSSION Moment

tensors are outputs of an inverse problem which can be calculated using different techniques with different strengths and weaknesses. In our analysis we considered catalogues obtained using

different approaches: for instance, the inversion procedure of the GCMT is mainly based on surface waveforms, while the ISC-GEM also derives focal mechanisms via body waves polarities and

amplitudes. The first method usually guarantees higher quality datasets since it takes advantage of the low-frequency information of the entire seismogram; on the other hand, it is rather

sensitive to the adopted seismic velocity model, which can introduce severe errors in the estimation of Mw < 5 earthquakes moment tensors50. In our analysis, we only considered reviewed

seismic events occurred in the last two decades with magnitudes Mw > 5 (compare with Table 1 for details) to guarantee a satisfactory data quality. This choice allows us to reject the

hypothesis of a uniform distribution of the DC component as a function of the rake angle, as proven by the significant _p_-values of the _χ_2 test for both the GCMT and the ISC-GEM

catalogues (_p_ ≪ 0.001, Table 1). Prudence is required because even though heterogeneities in source geometry become smaller and smaller with magnitude so that moment tensor inversions are

more consistent for large earthquakes, Kagan’s angles51 are still large for Mw 6 (up to 30°) in global catalogues and significant values (5°–15°) also affect the largest events. For this

reason, large numbers of events with significant magnitude are needed for keeping uncertainties as small as possible. Despite efforts, the issue of possible systematic errors which may

affect both the DC percentage and its uncertainty remains. In this regard, since a direct inspection is extremely complicated for global and large-scale regional catalogues in which uniform

criteria are adopted for the inversion algorithms, we focused on the strongest arguments against a physical origin of large percentages (>30%) of CLVD component in moment tensor solutions

of moderate and large earthquakes showing that, even though present, they are not sufficient to explain the variability of the non-DC components in moment tensors. The first argument is the

decrease of the non-DC component for larger earthquakes51. The plots in Fig. 1b, d prove something different; the decrease is limited to thrust and transpressive earthquakes, while it is

not observed in other faulting types, at least above magnitude 5.5. This observation suggests a physical reason for this phenomenon. For instance, the finite-source ruptures with variations

in rake and slip amplitude over the fault plane, or multiple rupture planes are known to lead to non-DC moment tensors38. A second argument regards the moment tensor inversion procedure,

which tend to use longer period seismic signals with increasing magnitudes46 reducing the resolution of the inversion producing an apparent smoothing of the earthquake fault rupture. This

effect may contribute to the progressive decrease of the non-DC components in thrust-faulting earthquakes; however, it does not explain why this phenomenon is not observed in other fault

types in the same range of magnitudes. Once again, it is possible that large seismic events, along subduction zones, may involve simpler seismogenic sources than those occurring in other

tectonic settings. Another observation concerns the lack of correlation between non-DC terms between moment tensor catalogues41. We calculated the correlation between the DC values of Mw 

> 5.5 earthquakes of the GCMT and ISC catalogues grouped as a function of the rake angle (intervals of 3°). The Pearson correlation coefficient _ρ_ ≃ 0.81 (compare with Fig. S1 in the

Supplementary Material) clearly states that the accuracy of the measurements of the components of the moment tensor is sufficient to achieve coherent results between different catalogues. An

additional non-physical effect on the inversion should be taken into account before exploring possible mechanisms affecting the composition of the moment tensors: the dip of faults produces

a bias in the estimation of the DC components due to the different radiated wave patterns. In fact, strike-slip events tend to very strongly radiate SH (Love) waves, but weak body waves,

while Rayleigh waves are more dominant in dip-slip mechanisms. For this reason, we also perform an investigation focusing on large (Mw ≥ 7.0) shallow (depth lower than 50 km) events listed

in the GCMT catalog. It shows a weak negative correlation between the values of the DC component of earthquakes and angle of dip of faults (Fig. 5). This effect introduces an underestimation

of DC values in strike-slip events; however, the residual distribution of double-couple percentages is not uniform as a function of the rake angle. Considering together the results shown in

Figs. 1–3, 5, normal-faulting and transtensional events have lower DC components, while thrust-faulting events are those with higher values in agreement with the outcomes reported in42.

Therefore, our results suggest that the variations in the composition of moment tensors may also have physical origins. Their interpretation is rather simple: the complexity of earthquake

ruptures statistically decreases from normal faulting, strike-slip to thrust-faulting earthquakes, being the last ones usually associated to sharper, more continuous faults with respect to

the previous tectonic settings characterized by multiple anastomosed faults and larger damage zones. This structural variation could explain why the coseismic slip along thrust faults shows

higher double couple. However, even inside the same faulting type, a certain degree of variability is observed. Figure 6 shows that thrust-faulting intraplate earthquakes have lower DC

components than subduction events, while there is not a statistically significant difference between mid-ocean and continental rifting events (Fig. 7). This explanation is coherent with

structural and physical observations of a broad fan of dynamic behaviors of seismicity and faulting in different tectonic regimes52 (Fig. 8). Continental normal faults can generate

earthquakes with maximum Mw around 7.5, lower than mid-ocean normal-faulting events (~ Mw 8.0); analogously, intraplate thrusts can nucleate events up to Mw 8.0–8.5, whereas subductions may

reach at least Mw 9.5 because of larger and more uniform active tectonic settings. Therefore, it is counterintuitive that thrusts can produce thinner damage zones and dislocation widths

(Fig. 8). This paradox can be explained by the different degree of complexity of the geological structures and seismogenic sources statistically affected by the local tectonic setting

because of various stress patterns53, different balances of forces generating long-term crustal motion along normal faults versus thrusts54 (i.e., mainly gravitational energy and elastic

energy respectively) and physical properties of rocks55. The wide range of possible rupture dynamics also raises concerns about the appropriateness of using a unique, average moment tensor

for representing earthquakes involving complex ruptures (e.g., simultaneous or cascade fault activations, with large, >30%, CLVD percentages). The most important reason is related to the

estimation of the size of earthquakes56. Because of the triangle inequality, $${M}^{{TH}} = {\int _{{t}_{0}}^{{t}_{f}}}\left[\begin{array}{ccc}{M}_{{rr}}\left(t\right) & {M}_{r\theta

}\left(t\right) & {M}_{r\varphi }\left(t\right)\\ {M}_{\theta r}\left(t\right) & {M}_{\theta \theta }\left(t\right) & {M}_{\theta \varphi }\left(t\right)\\ {M}_{\varphi

r}\left(t\right) & {M}_{\varphi \theta }\left(t\right) & {M}_{\varphi \varphi }\left(t\right)\end{array}\right]{dt}\,\leftrightarrow \,{M}_{0}^{{TH}}\\ = {\int

_{{t}_{0}}^{{t}_{f}}}{\int _{\varSigma }^{}}\,\mu \left(x,t\right)u\left(x,t\right)\,{d\varSigma}\,{dt}\,{\ge \,M}_{0}^{{OB}}\\ = {\int _{\varSigma }^{}}\,\mu

\left(x\right)u\left(x\right)\,{d\varSigma}\leftrightarrow {M}^{{OB}}=\left[\begin{array}{ccc}{M}_{{rr}} & {M}_{r\theta } & {M}_{r\varphi }\\ {M}_{\theta r} & {M}_{\theta \theta

} & {M}_{\theta \varphi }\\ {M}_{\varphi r} & {M}_{\varphi \theta } & {M}_{\varphi \varphi }\end{array}\right]$$ (1) the operational value of the seismic moment is an appropriate

estimation of the energy nucleated during coseismic slip only if the rupture occurs along a perfect fault plane, otherwise it is underestimated. _M__TH_ is the theoretical moment tensor

associated with the theoretical seismic moment \({M}_{0}^{{TH}}\), considering the activation of complex seismogenic structures, _M__OB_ is the output of moment tensor inversion (average),

\({M}_{0}^{{OB}}\) is the operational seismic moment, _μ_(_x_) is the local shear modulus, _u_(_x_) is the local slip in the position _x_, Σ is the fault surface obtained via moment tensor

inversion and interpretation of geophysical data, while _t_0 and _t__f_ represent the times at which nucleation begins and arrest occurs respectively. Therefore, average radiation

coefficients may differ significantly from the pattern produced by the real high-resolution shear slip in the case of roughly non-planar faulting, i.e., non-DC earthquakes (Fig. 9),

underestimating magnitudes. Our conclusions agree with the analysis reported in57. It shows that about ten thousand global event solutions updated from the GCMT catalogue to account for the

effects of Earth’s heterogeneity are featured by larger scalar moments and double-couple components than previously thought. Since a non-uniform distribution of the DC as a function of

magnitude has been highlighted in compressive and transcurrent tectonic settings, further analysis should be done in order to evaluate its impact on the scaling exponent of the

Gutenberg-Richter distribution, which we also proved to be negatively correlated to the percentage of DC. This effect might be an additional source of bias for the estimation of the b-value,

which is already subject to several other pitfalls58,59,60, reducing its potential reliability for seismic hazard assessment. CONCLUSIONS The increasing quality and completeness of global

moment tensor catalogues allow to enhance our knowledge of seismic processes delving into the connection between seismicity, tectonics, and faulting. In our analysis, we draw attention to

different compositions of the moment tensors of moderate and large seismic events as a function of the tectonic setting: thrusts host earthquakes with more elevated DC percentages with

respect to strike-slip and normal faults. The CLVD component decreases as the size of earthquakes increases in reverse faulting, while this trend is weaker or absent in other classes of

seismicity, with also an upstream behavior noticed in transcurrent earthquakes, likely due to noise in the inversion procedure. An apparent significant departure from planar shear, even

though of debated origin, is found to be positively correlated to the _b_-value and negatively related to the corner magnitude of the frequency-size distribution which is compatible with a

systematic magnitude underestimation in low DC earthquakes. Our results suggest that, at least for large seismic events featured by suspiciously high non-DC components (e.g., 30/10/2016 Mw

6.5 Norcia61 and 13/11/2016 Mw 7.8 Kaikoura62 earthquakes) should be considered to better assess their size accurately also because of possible impact on seismic forecasting. METHODS The DC

contributions are calculated starting from the moment tensor components63, so that, given the eigenvalues _M_1 > _M_2 > _M_3, the fractional components are given by

$$\left\{\begin{array}{c}{C}_{{ISO}}=\,\frac{{M}_{1}+\,{M}_{2}+{M}_{3}}{3\,M} \hfill \\ {C}_{{CLVD}}=\,\frac{2({M}_{1}+\,{M}_{3}-{2M}_{2})}{3\,M}\hfill\\

{C}_{{DC}}=\frac{{M}_{1}-{M}_{3}-\left|{M}_{1}+{M}_{3}-{2M}_{2}\right|}{2\,M}\end{array}\right.$$ (2) where \(M=|{C}_{{CLVD}}|+|{C}_{{ISO}}|+{C}_{{DC}}\). Only earthquakes with size above

the completeness magnitude are included in our analysis. Volcanic, anthropic, and collapse-related events are removed (ISO ≈ 0 in shear faulting). The error bars in Figs. 1, 2, 7, 8

represent the standard deviations for the mean of the DC percentages in each rake interval. The compositions of the moment tensors are assumed to be independent and identically distributed

within each rake interval, so that the uncertainties of the DC components are dominated by the statistical fluctuations at least for large catalogues. The classification of earthquakes

according to their focal mechanisms follows the classical definition by Aki and Richards29. An earthquake is a thrust-faulting event if its rake is in the range 90° ± 30°, while

normal-faulting earthquakes fall in −90° ± 30° and strike-slip events are in 0° ± 30°, ±180° ∓ 30°. The b-value is calculated according to the Tinti-Mulargia method64. DATA AVAILABILITY

Global and regional event databases are available at the following links: https://www.globalcmt.org/CMTsearch.html (GCMT), http://www.isc.ac.uk/iscbulletin/search/fmechanisms/ (ISC),

http://rcmt2.bo.ingv.it/ (RCMT), https://www.fnet.bosai.go.jp/event/search.php?LANG=en (NIED). CODE AVAILABILITY The calculation and analysis of double-couple components has been realized

using the software MATLAB® [https://it.mathworks.com/] version 9.10.0.1684407 (R2021a) Update 3 according to the procedure described in the section “Methods”. Scripts and source files are

available from the author [D.Z.] upon request. CHANGE HISTORY * _ 08 DECEMBER 2022 A Correction to this paper has been published: https://doi.org/10.1038/s43247-022-00647-8 _ REFERENCES *

Wang, K., Hu, Y. & He, J. Deformation cycles of subduction earthquakes in a viscoelastic Earth. _Nature_ 484, 327–332 (2012). Article  CAS  Google Scholar  * Doglioni, C. Geological

remarks on the relationships between extension and convergent geodynamic settings. _Tectonophysics_ 252, 253–267 (1995). Article  Google Scholar  * Leonard, M. Earthquake fault scaling:

self-consistent relating of rupture length, width, average displacement, and moment release. _Bull. Seismol. Soc. Am._ 100, 1971–1988 (2010). Article  Google Scholar  * Albano, M. et al.

Numerical analysis of interseismic, coseismic and post-seismic phases for normal and reverse faulting earthquakes in Italy. _Geophys. J. Int._ 225, 627–645 (2021). Article  Google Scholar  *

Sibson, R. H. Frictional constraints on thrust, wrench and normal faults. _Nature_ 249, 542–544 (1974). Article  Google Scholar  * Dewey, J. F. Extensional collapse of orogens. _Tectonics_

7, 1123–1139 (1988). Article  Google Scholar  * Dawers, N. H., Anders, M. H. & Scholz, C. H. Growth of normal faults: displacement-length scaling. _Geology_ 21, 1107–1110 (1993). Article

  Google Scholar  * Rodriguez Padilla, A. M., Oskin, M. E., Milliner, C. W. & Plesch, A. Accrual of widespread rock damage from the 2019 Ridgecrest earthquakes. _Nat. Geosci._ 15,

222–226 (2022). Article  CAS  Google Scholar  * Ross, Z. E., Hauksson, E. & Ben-Zion, Y. Abundant off-fault seismicity and orthogonal structures in the San Jacinto fault zone. _Sci.

Adv._ 3, e1601946 (2017). Article  Google Scholar  * Hatem, A. E., Cooke, M. L. & Toeneboehn, K. Strain localization and evolving kinematic efficiency of initiating strike-slip faults

within wet kaolin experiments. _J. Struct. Geol._ 101, 96-108 (2017). Article  Google Scholar  * Sanderson, D. J. Models of strain variation in nappes and thrust sheets: a review.

_Tectonophysics_ 88, 201–233 (1982). Article  Google Scholar  * Kim, Y. S., Peacock, D. C. & Sanderson, D. J. Fault damage zones. _J. Struct. Geol._ 26, 503–517 (2004). Article  Google

Scholar  * Sibson, R. H. Implications of fault-valve behaviour for rupture nucleation and recurrence. _Tectonophysics_ 211, 283–293 (1992). Article  Google Scholar  * Sibson, R. H. The edge

of failure: critical stress overpressure states in different tectonic regimes. _Geol. Soc. Spec. Publ._ 458, 131–141 (2017). Article  Google Scholar  * Doglioni, C., Barba, S., Carminati, E.

& Riguzzi, F. Fault on–off versus coseismic fluids reaction. _Geosci. Front._ 5, 767–780 (2014). Article  Google Scholar  * Mogi, K. The Influence of Dimensions of Specimens of the

Fracture Strength of Rocks-comparison between the Strength of Rock Specimens and that of the Earth’s Crust. _Bull. Earthq. Res. Inst., Univ. Tokyo_ 40, 175–185 (1962). Google Scholar  *

Scholz, C. H. The frequency-magnitude relation of microfracturing in rock and its relation to earthquakes. _Bull. Seismol. Soc. Am._ 58, 399–415 (1968). Article  Google Scholar  *

Schorlemmer, D., Wiemer, S. & Wyss, M. Variations in earthquake-size distribution across different stress regimes. _Nature_ 437, 539–542 (2005). Article  CAS  Google Scholar  * Amitrano,

D. Variability in the power-law distributions of rupture events. _Eur. Phys. J.-Spec. Top._ 205, 199–215 (2012). Article  Google Scholar  * Bird, P. & Kagan, Y. Y. Plate-tectonic

analysis of shallow seismicity: Apparent boundary width, beta, corner magnitude, coupled lithosphere thickness, and coupling in seven tectonic settings. _Bull. Seismol. Soc. Am._ 94,

2380–2399 (2004). Article  Google Scholar  * Chen, C. C., Wang, W. C., Chang, Y. F., Wu, Y. M. & Lee, Y. H. A correlation between the b-value and the fractal dimension from the

aftershock sequence of the 1999 Chi-Chi, Taiwan, earthquake. _Geophys. J. Int._ 167, 1215–1219 (2006). Article  Google Scholar  * Aki, K. A probabilistic synthesis of precursory phenomena.

_Earthquake Prediction: an International Review_ 4, 566–574 (1981). Google Scholar  * Allam, A. A., Kroll, K. A., Milliner, C. W. D. & Richards‐Dinger, K. B. Effects of fault roughness

on coseismic slip and earthquake locations. _J. Geophys. Res._ 124, 11336–11349 (2019). Article  Google Scholar  * Tal, Y. & Faulkner, D. The effect of fault roughness and earthquake

ruptures on the evolution and scaling of fault damage zones. _J. Geophys. Res._ 127, e2021JB023352 (2022). Article  Google Scholar  * Thakur, P. & Huang, Y. Influence of fault zone

maturity on fully dynamic earthquake cycles. _Geophys. Res. Lett._ 48, e2021GL094679 (2021). Article  Google Scholar  * Tahir, M. & Grasso, J. R. Faulting style controls for the

space–time aftershock patterns. _Bull. Seismol. Soc. Am._ 105, 2480–2497 (2015). Article  Google Scholar  * Zaccagnino, D., Telesca, L. & Doglioni, C. Scaling properties of seismicity

and faulting. _Earth & Planet. Sci. Lett._ 584, 117511 (2022). Article  CAS  Google Scholar  * Madariaga, R. High frequency radiation from dynamic earthquake. _Ann. Geophys._ 1, 17

(1983). Google Scholar  * Aki, K. & Richards, P. G. Quantitative seismology in _University Science Books_(2nd Ed.) 704 pp (2002). * Julian, B. R., Miller, A. D. & Foulger, G. R.

Non‐double‐couple earthquakes 1. _Theory. Rev. Geophys._ 36, 525–549 (1998). Article  Google Scholar  * Kagan, Y. Y. Fractal dimension of brittle fracture. _J. Nonlinear Sci._ 1, 1–16

(1991). Article  Google Scholar  * Robertson, M. C., Sammis, C. G., Sahimi, M. & Martin, A. J. Fractal analysis of three‐dimensional spatial distributions of earthquakes with a

percolation interpretation. _J. Geophys. Res._ 100, 609–620 (1995). Article  Google Scholar  * Telesca, L., Lapenna, V. & Macchiato, M. Mono-and multi-fractal investigation of scaling

properties in temporal patterns of seismic sequences. _Chaos Solit. Fractals_ 19, 1–15 (2004). Article  Google Scholar  * Kagan, Y. Y. Earthquakes: models, statistics, testable forecasts.

_John Wiley & Sons_ (2013). * Miller, A. D., Foulger, G. R. & Julian, B. R. Non‐double‐couple earthquakes 2. Observations. _Rev. Geophys._ 36, 551–568 (1998). Article  Google Scholar

  * Zahradnik, J., Sokos, E., Tselentis, G. A. & Martakis, N. Non‐double‐couple mechanism of moderate earthquakes near Zakynthos, Greece, April 2006; explanation in terms of complexity.

_Geophys. Prospect._ 56, 341–356 (2008). Article  Google Scholar  * Xu, W. et al. Transpressional rupture cascade of the 2016 Mw 7.8 Kaikoura earthquake, New Zealand. _J. Geophys. Res._ 123,

2396–2409 (2018). Article  Google Scholar  * Frohlich, C. Earthquakes with non-double-couple mechanisms. _Science_ 264, 804–809 (1994). Article  CAS  Google Scholar  * Kuge, K. & Lay,

T. Data‐dependent non‐double‐couple components of shallow earthquake source mechanisms: Effects of waveform inversion instability. _Geophys. Res. Lett._ 21, 9–12 (1994). Article  Google

Scholar  * Šílený, J. Resolution of non-double-couple mechanisms: Simulation of hypocenter mislocation and velocity structure mismodeling. _Bull. Seism. Soc. Am._ 99, 2265–2272 (2009).

Article  Google Scholar  * Panza, G. F. & Saraò, A. Monitoring volcanic and geothermal areas by full seismic moment tensor inversion: Are non‐double‐couple components always artefacts of

modelling? _Geophys. J. Int._ 143, 353–364 (2000). Article  Google Scholar  * Rösler, B. & Stein, S. Consistency of non‐double‐couple components of seismic moment tensors with

earthquake magnitude and mechanism. _Seismol. Soc. Am._ 93, 1510–1523 (2022). Google Scholar  * Frohlich, C. & Davis, S. D. How well constrained are well‐constrained T, B, and P axes in

moment tensor catalogs? _J. Geophys. Res._ 104, 4901–4910 (1999). Article  Google Scholar  * Dziewonski, A. M., Chou, T.-A. & Woodhouse, J. H. Determination of earthquake source

parameters from waveform data for studies of global and regional seismicity. _J. Geophys. Res._ 86, 2825–2852 (1981). Article  Google Scholar  * Ekström, G. & Dziewonski, A. M.

Centroid-moment tensor solutions for 35 earthquakes in western North America (1977-1983). _Bull. Seismol. Soc. Am._ 75, 23–39 (1985). Article  Google Scholar  * Ekström, G., Nettles, M.

& Dziewonski, A. M. The global CMT project 2004-2010: Centroid-moment tensors for 13,017 earthquakes. _Phys. Earth Planet. Inter._ 200-201, 1–9 (2012). Article  Google Scholar  *

Storchak, D. A. et al. Public release of the ISC-GEM global instrumental earthquake catalogue (1900–2009). _Seism. Res. Lett._ 84, 810–815 (2013). Article  Google Scholar  * Pondrelli, S.

European-Mediterranean Regional Centroid-Moment Tensors Catalog (RCMT) [Data set]. _Istituto Nazionale di Geofisica e Vulcanologia (INGV)_ https://doi.org/10.13127/rcmt/euromed (2002). *

Fukuyama, E., Ishida, S., Dreger, D. S. & Kawai, H. Automated seismic moment tensor determination by using on-line broadband seismic waveforms. _Zisin (J. Seismol. Soc. Jpn) Ser. 2_ 51,

149–156 (1998). Google Scholar  * Cesca, S., Buforn, E. & Dahm, T. Amplitude spectra moment tensor inversion of shallow earthquakes in Spain. _Geophys. J. Int._ 166, 839–854 (2006).

Article  Google Scholar  * Kagan, Y. Y. 3-D rotation of double-couple earthquake sources. _Geophys. J. Int._ 106, 709–716 (1991). Article  Google Scholar  * Kagan, Y. Y. Seismic moment

distribution revisited: I. Statistical results. _Geophys. J. Int._ 148, 520–541 (2002). Article  Google Scholar  * Sibson, R. H. Fault rocks and fault mechanisms. _J. Geol. Soc._ 133,

191–213 (1977). Article  Google Scholar  * Doglioni, C., Carminati, E., Petricca, P. & Riguzzi, F. Normal fault earthquakes or graviquakes. _Sci. Rep._ 5, 1–12 (2015). Article  Google

Scholar  * Neely, J. S. & Stein, S. Why do continental normal fault earthquakes have smaller maximum magnitudes? _Tectonophysics_ 809, 228854 (2021). Article  Google Scholar  * Ben‐Zion,

Y. Collective behavior of earthquakes and faults: Continuum‐discrete transitions, progressive evolutionary changes, and different dynamic regimes. _Rev. Geophys_. 46, RG4006 (2008). *

Sawade, L., Beller, S., Lei, W. & Tromp, J. Global centroid moment tensor solutions in a heterogeneous earth: the CMT3D catalogue. _Geophys. J. Int._ 231, 1727–1738 (2022). Article 

Google Scholar  * Daniel, G. Bias in magnitude for earthquakes with unknown focal mechanism. _Geophys. Prospect._ 62, 848–861 (2014). Article  Google Scholar  * Marzocchi, W., Spassiani, I.,

Stallone, A. & Taroni, M. How to be fooled searching for significant variations of the b-value. _Geophys. J. Int._ 220, 1845–1856 (2020). Article  Google Scholar  * Herrmann, M. &

Marzocchi, W. Inconsistencies and lurking pitfalls in the magnitude–frequency distribution of high‐resolution earthquake catalogs. _Seismol. Res. Lett._ 92, 909–922 (2021). Article  Google

Scholar  * Scognamiglio, L. et al. Complex fault geometry and rupture dynamics of the Mw 6.5, 30 October 2016, Central Italy earthquake. _J. Geophys. Res: Solid Earth_ 123, 2943–2964 (2018).

Article  Google Scholar  * Cesca, S. et al. Complex rupture process of the Mw 7.8, 2016, Kaikoura earthquake, New Zealand, and its aftershock sequence. _Earth Planet. Sci. Lett._ 478,

110–120 (2017). Article  CAS  Google Scholar  * Vavryčuk, V. Moment tensor decompositions revisited. _J. Seismol._ 19, 231–252 (2015). Article  Google Scholar  * Tinti, S. & Mulargia, F.

Confidence intervals of b values for grouped magnitudes. _Bull. Seismol. Soc. Am._ 77, 2125–2134 (1987). Google Scholar  * Wyss, M., Sammis, C. G., Nadeau, R. M. & Wiemer, S. Fractal

dimension and b-value on creeping and locked patches of the San Andreas fault near Parkfield, California. _Bull. Seismol. Soc. Am._ 94, 410–421 (2004). Article  Google Scholar  * Singh, A.

P., Roy, I. G., Kumar, S. & Kayal, J. R. Seismic source characteristics in Kachchh and Saurashtra regions of Western India: b-value and fractal dimension mapping of aftershock sequences.

_Nat. Hazards_ 77, 33–49 (2015). Article  Google Scholar  * Valerio, E., Tizzani, P., Carminati, E. & Doglioni, C. Longer aftershocks duration in extensional tectonic settings. _Sci.

Rep._ 7, 1–12 (2017). Article  CAS  Google Scholar  * Mondal, S. K., Roy, P. N. S., Catherine, J. K. & Pandey, A. K. Significance of fractal correlation dimension and seismic b-value

variation due to 15th July 2009, New Zealand earthquake of Mw 7.8. _Ann. Geophys._ 62, SE568–SE568 (2019). Article  Google Scholar  Download references ACKNOWLEDGEMENTS We thank the editors

and three anonymous reviewers for their priceless comments and suggestions. We are grateful to Antonella Cirella, Pasquale De Gori and Rita Di Giovambattista for fruitful discussions. The

research is supported by Sapienza University of Rome and INGV. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Earth Sciences Department, Sapienza University, Piazzale Aldo Moro, 5, Rome,

00185, Italy Davide Zaccagnino & Carlo Doglioni * Istituto Nazionale di Geofisica e Vulcanologia (INGV), Via di Vigna Murata, 605, Rome, 00143, Italy Carlo Doglioni Authors * Davide

Zaccagnino View author publications You can also search for this author inPubMed Google Scholar * Carlo Doglioni View author publications You can also search for this author inPubMed Google

Scholar CONTRIBUTIONS D.Z. performed the analyses, contributed to their interpretation, prepared the figures and the table, and wrote the initial draft of the paper. C.D. realized the

geological interpretation of results, prepared Fig. 8 and led the research project. D.Z. and C.D. conceived the key ideas and wrote the final paper. CORRESPONDING AUTHOR Correspondence to

Davide Zaccagnino. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. PEER REVIEW PEER REVIEW INFORMATION _Communications Earth & Environment_ thanks the

anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editors: Sylvain Barbot, Joe Aslin. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature

remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY MATERIAL RIGHTS AND PERMISSIONS OPEN ACCESS

This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as

long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third

party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the

article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright

holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Zaccagnino, D., Doglioni, C. The

impact of faulting complexity and type on earthquake rupture dynamics. _Commun Earth Environ_ 3, 258 (2022). https://doi.org/10.1038/s43247-022-00593-5 Download citation * Received: 21 June

2022 * Accepted: 18 October 2022 * Published: 30 October 2022 * DOI: https://doi.org/10.1038/s43247-022-00593-5 SHARE THIS ARTICLE Anyone you share the following link with will be able to

read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing

initiative