Message passing variational autoregressive network for solving intractable ising models

ABSTRACT Deep neural networks have been used to solve Ising models, including autoregressive neural networks, convolutional neural networks, recurrent neural networks, and graph neural

networks. Learning probability distributions of energy configuration or finding ground states of disordered, fully connected Ising models is essential for statistical mechanics and NP-hard

problems. Despite tremendous efforts, neural network architectures with abilities to high-accurately solve these intractable problems on larger systems remain a challenge. Here we propose a

variational autoregressive architecture with a message passing mechanism, which effectively utilizes the interactions between spin variables. The architecture trained under an annealing

framework outperforms existing neural network-based methods in solving several prototypical Ising spin Hamiltonians, especially for larger systems at low temperatures. The advantages also

come from the great mitigation of mode collapse during training process. Considering these difficult problems to be solved, our method extends computational limits of unsupervised neural

networks to solve combinatorial optimization problems. SIMILAR CONTENT BEING VIEWED BY OTHERS AUTOREGRESSIVE NEURAL-NETWORK WAVEFUNCTIONS FOR AB INITIO QUANTUM CHEMISTRY Article 31 March

2022 VARIATIONAL NEURAL ANNEALING Article 25 October 2021 THE AUTOREGRESSIVE NEURAL NETWORK ARCHITECTURE OF THE BOLTZMANN DISTRIBUTION OF PAIRWISE INTERACTING SPINS SYSTEMS Article Open

access 14 October 2023 INTRODUCTION Many deep neural networks have been used to solve Ising models1,2, including autoregressive neural networks3,4,5,6,7,8, convolutional neural networks9,

recurrent neural networks4,10, and graph neural networks11,12,13,14,15,16,17. The autoregressive neural networks model the distribution of high-dimensional vectors of discrete variables to

learn the target Boltzmann distribution18,19,20,21 and allow for direct sampling from the networks. However, recent works question the sampling ability of autoregressive models in highly

frustrated systems, with the challenge resulting from mode collapse22,23. The convolutional neural networks9 respect the lattice structure of the 2D Ising model and achieve good

performance3, but cannot solve models defined on non-lattice structures. Variational classical annealing (VCA)4 uses autoregressive models with recurrent neural networks (RNN)10 and

outperforms traditional simulated annealing (SA)24 in finding ground-state solutions to Ising problems. This advantage comes from the fact that RNN can capture long-range correlations

between spin variables by establishing connections between RNN cells in the same layer. Those cells need to be computed sequentially, which results in a very inefficient computation of VCA.

Thus, in a particularly difficult class of fully connected Ising models, Wishart planted ensemble (WPE)25, ref. 4 only solves problem instances with up to 32 spin variables. Since a

Hamiltonian with the Ising form can be directly viewed as a graph, it is intuitive to use graph neural networks (GNN)26,27,28 to solve it. While a GNN-based method16 has been employed in

combinatorial optimization problems with system sizes up to millions, which first encodes problems in Ising forms29 and then relaxes discrete variables into continuous ones to use GNN, some

researchers argue that this method does not perform as well as classical heuristic algorithms30,31. In fact, the maximum cut and maximum independent set problem instances with millions of

variables used in ref. 16 are defined on very sparse graphs and are not hard to solve31. Also, a naive combination of graph convolutional networks (GCN)28 and variational autoregressive

networks (VAN)3 (we denote it as ‘GCon-VAN’ in this work) is tried but performs poorly in statistical mechanics problems defined on sparse graphs8. Reinforcement learning has also been used

to find the ground state of Ising models32,33. In addition, recently developed Ising machines have been used to find the ground state of Ising models and have shown impressive performance34,

especially those based on physics-inspired algorithms, such as SimCIM (simulated coherent Ising machine)35,36 and simulated bifurcation (SB)37,38. Exploration of new methods to tackle Ising

problems of larger scale and denser connectivity is of great interest. For example, finding the ground states of Ising spin glasses on two-dimensional lattices can be exactly solved in

polynomial time, while ones in three or higher dimensions are a non-deterministic polynomial-time (NP) hard problem39. Ising models correspond to some problems defined on graphs, such as the

maximum independent set problems, whose difficulty in finding the ground state might depend on the node’s degree being larger than a certain value40,41. The design of neural networks to

solve Ising models on denser graphs would lead to the development of powerful optimization tools and further shed light on the computational boundary of deep-learning-assisted algorithms.

Due to the correspondence between Ising models and graph problems, existing Ising-solving neural network methods can be described by the message passing (MP) neural networks (MPNN)

framework42. MPNN can be used to abstract commonalities between them and determine the most crucial implementation details, which help to design more complex and powerful network

architectures. Therefore, we reformulate existing VAN-based network architectures into this framework and then explore more variants for designing new network architectures with meticulously

designed MP mechanisms to better solve intractable Ising models. Here, we propose a variational autoregressive architecture with a MP mechanism and dub it a message passing variational

autoregressive network (MPVAN). It can effectively utilize the interactions between spin variables, including whether there are couplings and coupling values, while previous methods only

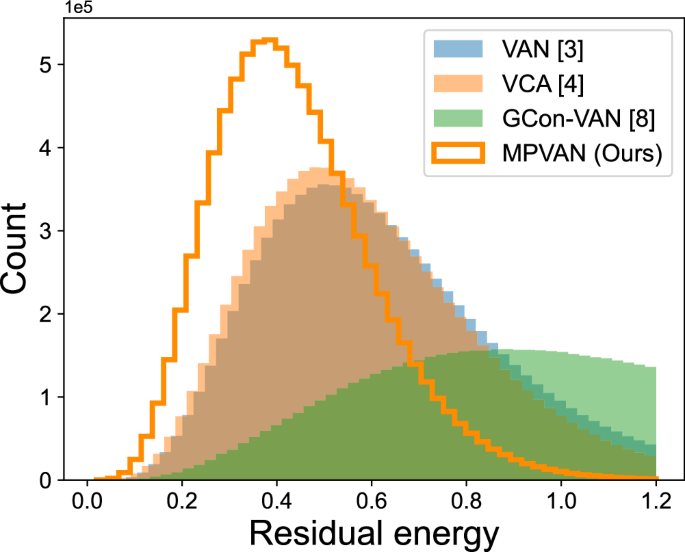
considered the former, i.e., the correlations. We show the residual energy histogram on the Wishart planted ensemble (WPE)25 with a rough energy landscape in Fig. 1. Compared to VAN3, VCA4,

and GCon-VAN8, the configurations sampled from MPVAN are concentrated on the regions with lower energy. Therefore, MPVAN has a higher probability of obtaining low-energy configurations,

which is beneficial for finding the ground state, and it is also what combinatorial optimization is concerned about. Numerical experiments show that our method outperforms the recently

developed autoregressive network-based methods VAN and VCA in solving two classes of disordered, fully connected Ising models with extremely rough energy landscapes, the WPE25 and the

Sherrington–Kirkpatrick (SK) model43, including more accurately estimating the Boltzmann distribution and calculating lower free energy at low temperatures. The advantages also come from the

great delay in the emergence of mode collapse during the training process of deep neural networks. Moreover, as the system size increases or the connectivity of graphs increases, MPVAN has

greater advantages over VAN and VCA in giving a lower upper bound to the energy of the ground state and thus can solve problems of larger sizes inaccessible to the methods reported

previously. Besides, with the same number of samples (which is via the forward process of the network for MPVAN and which is via Markov chain Monte Carlo for SA/parallel tempering

(PT)44,45,46,47,48,49), MPVAN outperforms classical heuristics SA and performs similarly or slightly better than advanced PT in finding the ground state of the extremely intractable WPE and

SK model. Compared to short-range Ising models such as the Edwards–Anderson model50, infinite-ranged interaction models (SK model and WPE) we considered are more challenging since there

exist many loops of different lengths, which leads to more complicated frustrations. Considering these extremely difficult problems to be solved, our method extends the current computational

limits of unsupervised neural networks51 to solve intractable Ising models and combinatorial optimization problems52. METHODS The message passing variational autoregressive network (MPVAN)

is to solve Ising models with the Hamiltonian as $$H=-\sum\limits_{\langle i,j\rangle }{J}_{ij}{s}_{i}{s}_{j},$$ (1) where \({\{{s}_{i}\}}_{i = 1}^{N}\in {\{\pm 1\}}^{N}\) are _N_ spin

variables, and 〈_i_, _j_〉 denotes that there is a non-zero coupling _J__i__j_ between _s__i_ and _s__j_. MPVAN is composed of an autoregressive MP mechanism and a variational autoregressive

network architecture, and its network architecture is shown in Fig. 2a. The input to MPVAN is a configuration \({{{{{{{\bf{s}}}}}}}}={\{{s}_{i}\}}_{i = 1}^{N}\) in a predetermined order of

spins, and the _i__t__h_ component of the output, \({\hat{s}}_{i}\), means the conditional probability of _s__i_ taking + 1 when given values of spins in front of it, S<_i_, i.e.,

\({\hat{s}}_{i}={q}_{\theta }({s}_{i}=+1| {{{{{{{{\bf{s}}}}}}}}}_{ < i})\). As in VAN3, the variational distribution of MPVAN is decomposed into the product of conditional probabilities

as $${q}_{\theta }({{{{{{{\bf{s}}}}}}}})=\prod\limits_{i=1}^{N}{q}_{\theta }({s}_{i}| {s}_{1},{s}_{2},\ldots ,{s}_{i-1}),$$ (2) where _q__θ_(S) represents the variational joint probability

and _q__θ_(_s__i_∣_s_1, _s_2, …, _s__i_−1) denotes the variational conditional probability, both of which are parametrized by trainable parameters _θ_. MPVAN LAYER MPVAN are constructed by

stacking multiple messages passing variational autoregressive network layers. A single MPVAN layer is composed of an autoregressive MP process and nonlinear functions with trainable

parameters defined by VAN3. The input to the MPVAN layer is a set of node features, \({{{{{{{\bf{h}}}}}}}}=\{{\overrightarrow{h}}_{1},{\overrightarrow{h}}_{2},\ldots

,{\overrightarrow{h}}_{N}\},{\overrightarrow{h}}_{i}\in {(0,1)}^{F}\), where _F_ is the number of training samples. The layer produces a new set of node features,

\({{{{{{{{\bf{h}}}}}}}}}^{o}=\{{\overrightarrow{h}}{_{1}^{o}},{\overrightarrow{h}}{_{2}^{o}},\ldots ,{\overrightarrow{h}}{_{N}^{o}}\},{\overrightarrow{h}}{_{i}^{o}}\in {{\mathbb{R}}}^{F}\),

as the output. For brevity, we set _F_ = 1 and donate \({\overrightarrow{h}}_{i}\) and \({\overrightarrow{h}}{_{i}^{o}}\) as _h__i_ and \({h}_{i}^{o}\), respectively. The H_o_ is obtained by

$${{{{{{{{\bf{h}}}}}}}}}^{o}=\sigma ({\langle {{{{{{{\bf{h}}}}}}}}\rangle }_{MP}W+b),$$ (3) where sigmoid activation function \(\sigma (x)=\frac{1}{1+{e}^{-x}}\) ranging in (0, 1) and thus

\({h}_{i}^{o}\in (0,1)\). The \({\langle {{{{{{{\bf{h}}}}}}}}\rangle }_{MP}=\{{\langle {h}_{1}\rangle }_{MP},{\langle {h}_{2}\rangle }_{MP},\ldots ,{\langle {h}_{N}\rangle }_{MP}\}\),

\({\langle {h}_{i}\rangle }_{MP}\in {\mathbb{R}}\), denotes the updated node features from H by MP. The _W_ and _b_ are layer-specific trainable parameters, and _W_ is a triangular matrix to

ensure the autoregressive property3,19,20,21. To show how to get 〈H〉_M__P_, we first review the MP mechanism defined in the MPNN framework42. We describe MP operations on the current layer

with node features _h__i_ and edge features _J__i__j_. The MP phase includes how to obtain neighboring messages _m__i_ and how to update node features _h__i_, which are defined as $${m}_{i}

=\, \sum\limits_{j\in {N}_{a}(i)}M({h}_{i},{h}_{j},{J}_{ij}),\\ {\langle {h}_{i}\rangle }_{MP} =U({h}_{i},{m}_{i}),$$ (4) where _h__j_ is the node feature of _j_, and $${N}_{a}(i)=\{\,j\,|

\,j \, < \, i,{J}_{ij} \,\ne\, 0\},$$ (5) which denotes the neighbors located before node _i_. The _N__a_(_i_) is used to preserve autoregressive property, which is different from general

MP mechanisms42 and graph neural networks28,53,54. The message aggregation function _M_(_h__i_, _h__j_, _J__i__j_) and node feature update function _U_(_h__i_, _m__i_) are different across

MP mechanisms. Now, existing autoregressive network-based methods can be reformulated into combinations of VAN and different MP mechanisms. Then, we explore their variants and propose our

method. In VAN3, there is no MP process from neighboring nodes. Therefore, the node features _h__i_ are updated according to $$\begin{array}{l}{m}_{i}=0,\\ {\langle {h}_{i}\rangle

}_{MP}={h}_{i},\end{array}$$ (6) which is the first MP mechanism in Fig. 2b. Another impressive variational autoregressive network approach is variational classical annealing (VCA)4, which

uses the dilated RNN architecture55 to take into account the correlations between hidden units in the same layer. VCA cannot be represented as a special MPVAN since the MP mechanisms for

utilizing features of neighboring nodes are free of trainable parameters, which are different from the ones in VCA. In GCon-VAN8, a combination of GCN28 and VAN, the \({\langle

{h}_{i}\rangle }_{MP}\) are obtained by $${m}_{i} =\, \sum\limits_{j\in {N}_{a}(i)}{A}_{ij}{h}_{j},\\ {\langle {h}_{i}\rangle }_{MP} =\, \frac{{m}_{i}+{h}_{i}}{deg(i)+1},$$ (7) where _A_ is

the adjacency matrix of the graph, and _d__e__g_(_i_) represents the degree of node _i_. The _h__i_ is updated based on the connectivity of the graph, which is the second MP mechanism in

Fig. 2b. However, GCon-VAN performs poorly on sparse graphs in calculating physical quantities such as correlations and free energy8 and it performs even worse on dense graphs in our trial.

It may be because GCon-VAN only considers connectivity and ignores the weights of neighboring node features. Also, from the results of VAN in Fig. 1, the node feature _h__i_ itself should be

highlighted rather than the small weight \(\frac{1}{deg(i)+1}\) in Eq. (7). Therefore, we explore more variants and propose three MP mechanisms. The _m__i_ are obtained by

$${m}_{i}=\sum\limits_{j\in {N}_{a}(i)}| {J}_{ij}| {h}_{j},$$ (8a) $${m}_{i}=\sum\limits_{j\in {N}_{a}(i)}{J}_{ij}{h}_{j},$$ (8b) $${m}_{i}=\sum\limits_{j\in

{N}_{a}(i)}{J}_{ij}{s}_{j}{h}_{j}^{{\prime} },$$ (8c) where $${h}_{j}^{{\prime} }=\frac{1+{s}_{j}}{2}{h}_{j}+\frac{1-{s}_{j}}{2}(1-{h}_{j}).$$ (9) In above three mechanisms, the \({\langle

{h}_{i}\rangle }_{MP}\) are obtained by $${\langle {h}_{i}\rangle }_{MP}=\frac{{m}_{i}}{{\sum }_{j\in {N}_{a}(i)}| {J}_{ij}| }+{h}_{i}.$$ (10) For the neighboring message _m__i_ in Eq. (8a),

we consider the weight of neighboring node features instead of averagely passing those features in Eq. (7). Also, we increase the weight of _h__i_ in Eq. (10) for all mechanisms we

designed. However, the Eq. (8a) ignores the influence of the sign of couplings {_J__i__j_}. Thus, we propose the MP mechanism made of Eq. (8b) and Eq. (10), which is the third MP mechanism

in Fig. 2b. It uses the values of couplings {_J__i__j_} in the Hamiltonian to weight the neighboring node features. Since it is based on the graph defined by the target Hamiltonian, we dub

it ‘graph MP mechanism’ (Graph MP). Previous methods and the above two MP mechanisms we designed do not make full use of the interactions between spin variables of the Hamiltonian in Eq.

(1), and known values of S<_i_ when updating the _h__i_. Intuitively, it may be helpful to consider those interactions and values of S<_i_ in the MP process. Therefore, we propose the

Hamiltonians MP mechanism composed of Eq. (8c) and Eq. (10), which is the fourth MP mechanism in Fig. 2b and also the mechanism used in MPVAN. The _s__j_ = ± 1 is the known value of the

neighboring spin _j_, and \({h}_{j}^{{\prime} }\in (0,1)\) represents the probability of the spin _j_ taking _s__j_. Based on the above definitions, it is reasonable to use

\({h}_{j}^{{\prime} }\) rather than _h__j_ in MP. To illustrate, suppose for the neighboring spin _j_, _s__j_ = − 1 and _h__j_ = 0.2. Then, if we repeatedly sample spin _j_, we could obtain

_s__j_ = − 1 with a probability of 0.8. It means that neighboring spin _j_ should have a greater impact on _h__i_ when it takes − 1 than + 1, but _h__j_ = 0.2 is not as good as

\({h}_{j}^{{\prime} }=0.8\) to reflect the great importance of _s__j_ = − 1. On the other hand, suppose for the neighboring spin _j_, _s__j_ = − 1 and _h__j_ = 0.8. We could obtain _s__j_ = 

− 1 with a probability of 0.2 if we sample spin _j_ again. At this time, using \({h}_{j}^{{\prime} }\) instead of _h__j_ could show little importance of _s__j_ = − 1. So we think it makes

sense to use \({h}_{j}^{{\prime} }\) to reflect the effect of the spin _j_ taking _s__j_ in MP. Taking the graph with 4 nodes and 3 edges in Fig. 2b as an example, applying the above four MP

mechanisms, the \({\langle {h}_{3}\rangle }_{MP}\) are obtained as $${\langle {h}_{3}\rangle }_{MP\,in\,VAN}={h}_{3},$$ (11a) $${\langle {h}_{3}\rangle

}_{MP\,in\,GCon-VAN}=\frac{{h}_{1}+{h}_{2}+{h}_{3}}{3},$$ (11b) $${\langle {h}_{3}\rangle }_{{{{{{\rm{Graph}}}}}}\,MP}=\frac{{J}_{31}{s}_{1}{h}_{1}+{J}_{32}{s}_{2}{h}_{2}}{| {J}_{31}| +|

{J}_{32}| }+{h}_{3},$$ (11c) $${\langle {h}_{3}\rangle }_{{{{{{\rm{Hamiltonians}}}}}}\,MP}=\frac{{J}_{31}{s}_{1}{h}_{1}^{{\prime} }+{J}_{32}{s}_{2}{h}_{2}^{{\prime} }}{| {J}_{31}| +|

{J}_{32}| }+{h}_{3}.$$ (11d) We also consider more MP mechanisms and compare their performance in Supplementary Note I, where Hamiltonians MP always performs best. In addition, since an

arbitrary MP variational autoregressive network is constructed through stacking MPVAN layers, we also discuss the effect of the number of layers on the performance. MPVAN exhibits

characteristics similar to GNN, i.e., there exists an optimal number of layers, which can be found in Supplementary Note II. TRAINING MPVAN We then describe how to train MPVAN. In alignment

with the variational approach employed in VAN, the variational free energy _F__q_ is used as loss function, $${F}_{q}=\sum\limits_{{{{{{{{\bf{s}}}}}}}}}{q}_{\theta

}({{{{{{{\bf{s}}}}}}}})\left[E({{{{{{{\bf{s}}}}}}}})+\frac{1}{\beta }\ln {q}_{\theta }({{{{{{{\bf{s}}}}}}}})\right],$$ (12) where _β_ = 1/_T_ is inverse temperature, and _E_(S) is the _H_ of

Eq. (1) related to a given configuration S. The configuration S follows Boltzmann distribution _p_(S) = _e_−_β__E_(S)/_Z_, where _Z_ = ∑S_e_−_β__E_(S). Since the Kullback–Leibler (KL)

divergence between the variational distribution _q__θ_ and the Boltzmann distribution _p_ is defined as \({D}_{KL}({q}_{\theta }| | p)={\sum }_{{{{{{{{\bf{s}}}}}}}}}{q}_{\theta

}({{{{{{{\bf{s}}}}}}}})\ln (\frac{{q}_{\theta }({{{{{{{\bf{s}}}}}}}})}{p({{{{{{{\bf{s}}}}}}}})})=\beta ({F}_{q}-F)\) and is always non-negative, _F__q_ is the upper bound to the free energy

\(F=-(1/\beta )\ln Z\). The gradient of _F__q_ with respect to the parameters _θ_ is $${\bigtriangledown }_{\theta }{F}_{q}=\sum\limits_{{{{{{{{\bf{s}}}}}}}}}{q}_{\theta

}({{{{{{{\bf{s}}}}}}}})\left\{\left[E({{{{{{{\bf{s}}}}}}}})+\frac{1}{\beta }\ln {q}_{\theta }\left.({{{{{{{\bf{s}}}}}}}})\right)\right]{\bigtriangledown }_{\theta }\ln {q}_{\theta

}({{{{{{{\bf{s}}}}}}}})\right\}.$$ (13) With the computed gradients ▽_θ__F__q_, we iteratively adjust the parameters of the networks until the _F__q_ stops decreasing. MPVAN is trained under

an annealing framework, i.e., starting from the initial inverse temperature _β_initial and gradually decreasing the temperature by annealing _N_annealing steps until the end temperature

_β_final. We linearly increase the inverse temperature with a step of _β__i__n__c_. During each annealing step, we decrease the temperature and subsequently apply _N_training

gradient-descent steps to update the network parameters using Adam optimizer51, thereby minimizing the variational free energy _F__q_. As with the VAN3, the network is trained using the data

produced by itself, and at each training step, _N_samples samples are drawn from the networks for training. After training, we can sample directly from the network to calculate the upper

bound to the free energy and other physical quantities such as entropy and correlations. THEORETICAL ANALYSIS FOR MPVAN Compared to VAN3, MPVAN has an additional Hamiltonians MP process. In

this section, we will provide a theoretical and mathematical analysis of the advantages of the Hamiltonians MP mechanism in MPVAN in Corollary 1 below. The goal of MPVAN is to be able to

accurately estimate the Boltzmann distribution, i.e., configurations with low energy have a high probability and configurations with high energy have a low probability. Specifically, MPVAN

is trained by minimizing the variational free energy _F__q_, composed of \({{\mathbb{E}}}_{{{{{{{{\bf{s}}}}}}}} \sim {q}_{\theta }({{{{{{{\bf{s}}}}}}}})}E({{{{{{{\bf{s}}}}}}}})\) and

\({{\mathbb{E}}}_{{{{{{{{\bf{s}}}}}}}} \sim {q}_{\theta }({{{{{{{\bf{s}}}}}}}})}\ln {q}_{\theta }({{{{{{{\bf{s}}}}}}}})\). COROLLARY 1 The Hamiltonians MP process makes

\({{\mathbb{E}}}_{{{{{{{{\bf{s}}}}}}}} \sim {q}_{\theta }({{{{{{{\bf{s}}}}}}}})}E({{{{{{{\bf{s}}}}}}}})\) and \({{\mathbb{E}}}_{{{{{{{{\bf{s}}}}}}}} \sim {q}_{\theta

}({{{{{{{\bf{s}}}}}}}})}\ln {q}_{\theta }({{{{{{{\bf{s}}}}}}}})\) smaller, and therefore variational free energy _F__q_ smaller compared to no MP. PROOF We discuss MP process that makes

\({{\mathbb{E}}}_{{{{{{{{\bf{s}}}}}}}} \sim {q}_{\theta }({{{{{{{\bf{s}}}}}}}})}E({{{{{{{\bf{s}}}}}}}})\) and \({{\mathbb{E}}}_{{{{{{{{\bf{s}}}}}}}} \sim {q}_{\theta

}({{{{{{{\bf{s}}}}}}}})}\ln {q}_{\theta }({{{{{{{\bf{s}}}}}}}})\) smaller separately. STEP 1: Making \({{\mathbb{E}}}_{{{{{{{{\bf{s}}}}}}}} \sim {q}_{\theta

}({{{{{{{\bf{s}}}}}}}})}E({{{{{{{\bf{s}}}}}}}})\) smaller. When training MPVAN, it is impossible to exhaust all configurations to calculate the variational free energy _F__q_, so we use the

mathematical expectation of training samples to estimate it. Therefore, we have $${{\mathbb{E}}}_{{{{{{{{\bf{s}}}}}}}} \sim {q}_{\theta

}({{{{{{{\bf{s}}}}}}}})}E({{{{{{{\bf{s}}}}}}}})=\frac{1}{{N}_{samples}}\sum\limits_{k=1}^{{N}_{samples}}E({{{{{{{{\bf{s}}}}}}}}}_{k}),$$ (14) where S_k_ is _k__t__h_ training samples and

_N_samples is the number of training samples. Consider the Hamiltonians MP process (composed of Eq. (8c) and Eq. (10)) for updating the _h__i_ as an example to analyze how MP makes

\({{\mathbb{E}}}_{{{{{{{{\bf{s}}}}}}}} \sim {q}_{\theta }({{{{{{{\bf{s}}}}}}}})}E({{{{{{{\bf{s}}}}}}}})\) smaller. Since the MP process maintains autoregressive property, making _E_(S)

smaller for any configuration is equivalent to making the local Hamiltonian defined as _H_local = − ∑_j_<_i__J__i__j__s__i__s__j_ smaller, when given the values of its neighboring spins

S<_i_. Since _H__l__o__c__a__l_ = − _s__i_∑_j_<_i__J__i__j__s__j_ with known ∑_j_<_i__J__i__j__s__j_, we are concerned about how the MP affects the probability of _s__i_ taking +1

or −1. According to Eq. (10), the value of \({\sum }_{j < i}{J}_{ij}{s}_{j}{h}_{j}^{{\prime} }\) plays an important role in that, and we discuss it in 2 cases. _Case_ 1: if \({\sum }_{j

< i}{J}_{ij}{s}_{j}{h}_{j}^{{\prime} } \, > \, 0\), then according to Eq. (10), we have $${\langle {h}_{i}\rangle }_{MP} \, > \, {h}_{i},$$ (15) i.e., $$Pr[{\langle {s}_{i}\rangle

}_{MP}=+1| {{{{{{{{\bf{s}}}}}}}}}_{ < i}] \, > \, Pr[{s}_{i}=+1| {{{{{{{{\bf{s}}}}}}}}}_{ < i}],$$ (16) where $${\langle {s}_{i}\rangle }_{MP}={{{{{\rm{Bernoulli}}}}}}({\langle

{h}_{i}\rangle }_{MP}),$$ (17a) $${s}_{i}={{{{{\rm{Bernoulli}}}}}}({h}_{i}).$$ (17b) The Bernoulli(_p_) denotes sampling from the Bernoulli distribution to output +1 with a probability _p_.

Thus, we have $$Pr[{\langle {H}_{{{{{\rm{local}}}}}}^{{\prime} }\rangle }_{MP} \, < \, 0] \, > \, Pr[{H}_{{{{{\rm{local}}}}}}^{{\prime} } \, < \, 0],$$ (18) where $${\langle

{H}_{{{{{\rm{local}}}}}}^{{\prime} }\rangle }_{MP}=-{\langle {s}_{i}\rangle }_{MP}\sum\limits_{j < i}{J}_{ij}{s}_{j}{h}_{j}^{{\prime} },$$ (19a) $${H}_{{{{{\rm{local}}}}}}^{{\prime}

}=-{s}_{i}\sum\limits_{j < i}{J}_{ij}{s}_{j}{h}_{j}^{{\prime} },$$ (19b) and _P__r_[ ⋯  ] denotes the probability of something. _Case_ 2: if \({\sum }_{j <

i}{J}_{ij}{s}_{j}{h}_{j}^{{\prime} } < 0\), then according to Eq. (10), we have $${\langle {h}_{i}\rangle }_{MP} \, < \, {h}_{i},$$ (20) i.e., $$Pr[{\langle {s}_{i}\rangle }_{MP}=-1|

{{{{{{{{\bf{s}}}}}}}}}_{ < i}] \, > \, Pr[{s}_{i}=-1| {{{{{{{{\bf{s}}}}}}}}}_{ < i}],$$ (21) and also obtain the Eq. (18). Therefore, regardless of the value of \({\sum }_{j <

i}{J}_{ij}{s}_{j}{h}_{j}^{{\prime} }\), MP process always makes \({H}_{{{{{\rm{local}}}}}}^{{\prime} }\) smaller compared with no MP. It can be found that the difference between _H_local and

\({H}_{{{{{\rm{local}}}}}}^{{\prime} }\) is that the latter has \({h}_{j}^{{\prime} }\). It encapsulates more information about the spin _j_ beyond the current configuration spin value

_s__j_, which can indicate how much influence the message corresponding to the neighboring node features _h__j_ has on \({\langle {h}_{i}\rangle }_{MP}\) and, combining with the coupling

_J__i__j_, performs a weighted MP. Thus, although not identical, it is possible to predict _H__l__o__c__a__l_ through \({H}_{{{{{\rm{local}}}}}}^{{\prime} }\) and thus we get the conclusion

that Hamiltonians MP mechanism makes local Hamiltonian smaller. STEP 2: Making \({{\mathbb{E}}}_{{{{{{{{\bf{s}}}}}}}} \sim {q}_{\theta }({{{{{{{\bf{s}}}}}}}})}\ln {q}_{\theta

}({{{{{{{\bf{s}}}}}}}})\) smaller. Similar to \({{\mathbb{E}}}_{{{{{{{{\bf{s}}}}}}}} \sim {q}_{\theta }({{{{{{{\bf{s}}}}}}}})}E({{{{{{{\bf{s}}}}}}}})\), we have

$${{\mathbb{E}}}_{{{{{{{{\bf{s}}}}}}}} \sim {q}_{\theta }({{{{{{{\bf{s}}}}}}}})}\ln {q}_{\theta

}({{{{{{{\bf{s}}}}}}}})=\frac{1}{{N}_{{{{{\rm{samples}}}}}}}\sum\limits_{k=1}^{{N}_{{{{{\rm{samples}}}}}}}\ln {q}_{\theta }({{{{{{{{\bf{s}}}}}}}}}_{k}).$$ (22) The second derivative of

\(y(x)=\ln (x)\) is _y_(_x_)(2) = −1/_x_2 and thus _y_(_x_) is concave down, which satisfies \(\frac{y(a)+y(b)}{2} < y(\frac{a+b}{2})\)56,57. From the analysis of STEP 1, the MP process

improves (reduces) the probability of configurations with low (high) energy. Therefore, MP makes \({\sum }_{k = 1}^{{N}_{{{{{\rm{samples}}}}}}}\ln {q}_{\theta }({{{{{{{{\bf{s}}}}}}}}}_{k})\)

smaller compared to no MP. □ In summary, combining the analyses of STEP 1 and STEP 2, the MP process makes the variational free energy _F__q_ smaller compared to no MP. RESULTS Since

Hamiltonians MP always performs best, as shown in Supplementary Note I, we only consider this MP mechanism in the following numerical experiments. In addition, for simplicity, we always use

VCA to refer to VCA with the dilated RNN4. We first experimented on the Wishart planted ensemble (WPE)25. The WPE is a class of fully connected Ising models with an adjustable difficulty

parameter _α_ and two planted solutions that correspond to the two ferromagnetic states, which makes it an ideal benchmark problem for evaluating heuristic algorithms. The Hamiltonian of the

WPE is defined as $$H=-\frac{1}{2}\sum\limits_{i\ne j}{J}_{ij}{s}_{i}{s}_{j},$$ (23) where the coupling matrix {_J__i__j_} is a symmetric matrix and satisfies copula distribution. More

details about the WPE can be found in ref. 25. First, we discuss an important issue, mode collapse, which occurs when the target probability distribution has multiple peaks but networks only

learn a few of them. It severely affects the sampling ability of autoregressive neural networks23. Entropy is commonly used in physics to measure the degree of chaos in a system. The

greater the entropy, the more chaotic the system. Therefore, we can use the magnitude of entropy to reflect whether mode collapse occurs for the variational distribution. In our experiments,

we investigate how the negative entropy, a part of variational free energy _F__q_ in Eq. (12), changes during training, which is defined as

$$-S=\sum\limits_{{{{{{{{\bf{s}}}}}}}}}{q}_{\theta }({{{{{{{\bf{s}}}}}}}})\ln {q}_{\theta }({{{{{{{\bf{s}}}}}}}}),$$ (24) where _S_ is entropy. Equivalently, the smaller the negative

entropy, the better the diversity of solutions. As shown in Fig. 3, the change of −_S_ from MPVAN shows an increasing-decreasing-increasing trend, while −_S_ from other methods is monotonely

increasing and quickly convergent. When _t__r__a__i__n__i__n__g __s__t__e__p_ ≥ 500, mode collapse occurs for other methods, while until _t__r__a__i__n__i__n__g __s__t__e__p_ ≥ 2000, it

occurs for MPVAN. Therefore, MPVAN delays the emergence of mode collapse greatly. In addition, we also consider the impact of learning rates on the emergence of mode collapse in

Supplementary Note X, where mode collapse always occurs later in MPVAN than in VAN. Next, we benchmark MPVAN with existing methods when calculating the upper bound to the energy of the

ground state, i.e., finding a configuration S to minimize the Hamiltonian in Eq. (23), which is also the core concern of combinatorial optimization. To facilitate a quantitative comparison,

we employ the concept of residual energy, defined as $${\epsilon }_{{{{{\rm{res}}}}}}={\left[{\left\langle {H}_{{{{{\rm{min}}}}}}\right\rangle

}_{{{{{\rm{ava}}}}}}-{E}_{G}\right]}_{{{{{\rm{ava}}}}}},$$ (25) where _H_min represents the minimum value of the Hamiltonians corresponding to 106 configurations sampled directly from the

network after training, and _E__G_ is the energy of the ground state. The \({\left\langle \ldots \right\rangle }_{{{{{\rm{ava}}}}}}\) denotes the average over 30 independent runs for one

same instance, and \({\left[\ldots \right]}_{ava}\) means averaging on 30 instances. In Figs. 4 and 5, the solid line indicates the average value of the residual energy from 30 instances and

each for 30 independent runs, and the color band indicates the area between the maximum and minimum values of the residual energy of 30 independent runs for the corresponding algorithm.

Both solid lines and color bands are obtained by averaging 30 instances. As in Fig. 4a, the residual energy obtained by our method consistently is lower than that of VAN, VCA, and SA across

all system sizes when averaging 30 instances and each for 30 runs. Even compared with advanced parallel tempering (PT)44,45,46,47,48,49, MPVAN also exhibits similar or slightly better

performance in terms of average residual energy, and significantly better in terms of minimum residual energy. For WPE instances with system size _N_ = 50, MPVAN can still find the ground

state with non-ignorable probability, but other methods cannot. As the system size increases, MPVAN has greater advantages over VAN and VCA in giving a lower residual energy. Since the

number of interactions between spin variables is ∣{_J__i__j_ ≠ 0}∣ = _N_2 for fully connected systems, larger systems have many more interactions between spin variables. The advantages

indicate that using MPVAN to consider these interactions performs better in rougher energy landscapes. We always average 30 instances to reflect the general properties of models, and the

differences between instances can be seen in Supplementary Note I. Also, each method runs independently 30 times on the same instances to weaken the influence of occasionality in the

heuristics training, which can be found in Supplementary Note III. Since these methods are trained in different ways and on different hardware, we keep the total number of training samples

used in training and final sampling after training the same for all methods to achieve a relatively fair comparison. For SA/PT, it is the number of Monte Carlo steps. The training samples of

MPVAN consist of two parts, training samples and final sampling samples. Assuming annealing _N_annealing times, training _N_training steps at each temperature, sampling _N_samples samples

each step in training, and final sampling _N_finsam samples, the total number of training samples for MPVAN is $${N}_{{{{{{\rm{MPsam}}}}}}}={N}_{{{{{\rm{annealing}}}}}}\times

{N}_{{{{{\rm{training}}}}}}\times {N}_{{{{{\rm{samples}}}}}}+{N}_{{{{{\rm{finsam}}}}}}.$$ (26) The training samples for VAN and VCA are the same as those for MPVAN, with some fine-tuning of

parameters. Assuming the number of inner loops of SA is _N_inlop at each temperature, and the total number of training samples for SA is

$${N}_{{{{{\rm{SAsam}}}}}}={N}_{{{{{\rm{annealing}}}}}}\times {N}_{{{{{\rm{inlop}}}}}}.$$ (27) Assuming the number of chains of PT is _N_chain, and the Markov chain Monte Carlo iterations at

each chain is _N__M__C_, then the number of training samples for PT is $${N}_{{{{{\rm{PTsam}}}}}}={N}_{{{{{\rm{chain}}}}}}\times {N}_{MC}.$$ (28) Therefore, corresponding to 1 run of MPVAN,

SA runs ⌈_N_MPsam/_N_SAsam⌉ times independently, and PT runs ⌈_N_MPsam/_N_PTsam⌉ times independently, and then they output their respective best results to benchmark MPVAN. For each

benchmark algorithm, we have fine-tuned the training parameters to maximize its best performance. Moreover, we compare the time-to-target (TTT) metric commonly used in the hardware

community. For finding the target values, MPVAN uses fewer iterations and training samples than PT, SA, VAN, and VCA, but it takes longer compared to PT. More results and details about the

TTT metric can be found in Supplementary Note VI. We also experiment on the Sherrington–Kirkpatrick (SK) model43, which is one of the most famous fully connected spin glass models and has

significant relevance in combinatorial optimization and machine learning applications58,59. Its Hamiltonian is also in the form of Eq. (23), where each coupling _J__i__j_ is randomly

generated from Gaussian distribution with the variance 1/_N_ and the coupling matrix is symmetric. As in Fig. 4b, our method provides significantly lower residual energy than VAN and SA

across all system sizes when averaging 30 instances each for 10 runs. Notably, as the system size increases, the advantages of our method over VAN and SA become even more pronounced, which

is consistent with the trend observed in WPE experiments. Compared to advanced PT, our method achieves close performance. We also show the approximating ratio results on the WPE and the SK

model in Supplementary Note IV, which is of concern to researchers of combinatorial optimization problems. We also use discrete simulated bifurcation (dSB)37, a physics-inspired Ising

machine, as a benchmark algorithm to achieve a more comprehensive performance evaluation of MPVAN. MPVAN achieves higher accuracy than dSB for the same runtime on the WPE with _N_ = 90 and

the SK model with _N_ = 300. It should be noted that dSB has a short single computation time and, therefore, has significant advantages in solving large-scale problems. More results and

details about dSB can be found in Supplementary Note VII. Inspired by the correlations between node’s degree and difficulty in finding the ground state in maximum independent set

problems40,41, in addition to experimenting on fully connected models, we also consider experiments on models with different connectivity, i.e., degrees of nodes in graphs. Since the SK

model has been widely studied, designing models based on it may be meaningful. We construct models defined on graphs with different connectivity by deleting some couplings of the SK model

and naming them variants of the SK model. Its Hamiltonian is in the form of Eq. (1), where each coupling _J__i__j_ is randomly generated from Gaussian distribution with the variance of 1/_N_

and the coupling matrix is symmetric. At each degree, we always randomly generate 30 instances each for 10 runs. As shown in Fig. 5, our method gives a lower residual energy than VAN and SA

at all degrees. Moreover, as the degree increases, the advantages of our method over VAN and SA become even more pronounced. The denser the graph, the larger the number of interactions

between spin variables. The advantages show that our method, which takes into account these interactions, is able to give lower upper bounds to the free energy. Also, MPVAN achieved

performance close to the advanced PT, and the poor performance of the PT on the sparsest problems used in this work may be related to the fact that the hyperparameters of the PT are not easy

to choose at this time. More details about the PT implementation can be found in Supplementary Note VIII. In the following, we focus on estimating the Boltzmann distribution and calculating

the free energy as annealing. As a proof of concept, we use the WPE with a small system size of _N_ = 20, where 2_N_ configurations can be enumerated, and the exact Boltzmann distribution

and exact free energy _F_ can be calculated within an acceptable time. We set _α_ = 0.05, and thus it is difficult to find the ground state due to strong low-energy degeneracy. As shown in

Fig. 6, when the temperature is high, i.e., when _β_ is small, the _D__K__L_(_q__θ_∣∣_p_) and the relative errors of _F__q_ relative to exact free energy _F_ from MPVAN, VAN, and VCA are

particularly small. Therefore, it is necessary to lower the temperature to distinguish them. As the temperature decreases, the probability of the configurations with low (high) energy in the

Boltzmann distribution increases (decreases), thus making it more difficult for neural networks to estimate the Boltzmann distribution. However, we find that the _D__K__L_(_q__θ_∣∣_p_)

obtained by our method is much smaller than that of VAN and VCA, which indicates that the variational distribution _q__θ_(S) parameterized by our method is closer to the Boltzmann

distribution. Similarly, our method gives a better estimation of free energy than VAN and VCA. These results illustrate that our method takes into account the interactions between spin

variables through MP and is more accurate in estimating the relevant physical quantities. CONCLUSIONS In summary, we propose a variational autoregressive architecture with a MP mechanism,

which can effectively utilize the interactions between spin variables, to solve intractable Ising models. Numerical experiments show that our method outperforms the recently developed

autoregressive network-based methods VAN and VCA in more accurately estimating the Boltzmann distribution and calculating lower free energy at low temperatures on two fully connected and

intractable Ising spin Hamiltonians, WPE, and the SK model. The advantages also come from the great mitigation of mode collapse during the training process of deep neural networks. Moreover,

as the system size increases or the connectivity of graphs increases, MPVAN has greater advantages over VAN and VCA in giving a lower upper bound to the energy of the ground state and thus

can solve problems of larger sizes inaccessible to the methods reported previously. Besides, with the same number of samplings (which is via the forward process of the network for MPVAN and

which is via Markov chain Monte Carlo for SA/PT), MPVAN outperforms classical heuristics SA and performs similarly or slightly better than advanced PT in finding the ground state of the

extremely intractable WPE and SK model, which illustrates the enormous potential of autoregressive networks in solving Ising models and combinatorial optimization problems. Formally, MPVAN

and GNN are similar. We notice that some researchers have recently argued that graph neural networks do not perform as well as classical heuristic algorithms on combinatorial optimization

problems30,31 for the method in ref. 16. Our work, however, draws the opposite conclusion. We argue that when the problems are in rough energy landscapes and hard to find the ground state

(e.g., WPE), our method performs significantly better than traditional heuristic algorithms such as SA and even similarly or slightly better than advanced PT. Our method is based on

variational autoregressive networks, which are difficult to train due to slow speed when the systems are particularly large, and thus MPVAN is not easy to expand to very large problems. At

the very least, we argue that MPVAN (or GNN) excels particularly well in certain intractable Ising models with rough energy landscapes and finite size, providing an alternative to

traditional heuristics. Theoretically, being the same with VAN, the computational complexity of MPVAN is _O_(_N_2), due to the nearly fully connected relationship between neighboring hidden

layers when dealing with fully connected models, while VCA with dilated RNNs is \(O(N\log (N))\). It might be interesting to explore how to reduce the computational complexity of MPVAN. In

algorithm implementation, hidden units from the same layer in MPVAN can be computed at once, while hidden units in VCA must be computed sequentially due to the properties of the RNN

architecture. More details about the computational speed of MPVAN, VAN, and VCA can be found in Supplementary Note V. DATA AVAILABILITY The data that support the findings of this study are

available from the corresponding author upon reasonable request. CODE AVAILABILITY The code that supports the findings of this study is available from the corresponding author upon

reasonable request. The hyperparameters we use are provided in Supplementary Note IX. REFERENCES * Carleo, G. et al. Machine learning and the physical sciences. _Rev. Mod. Phys._ 91, 045002

(2019). Article  ADS  Google Scholar  * Tanaka, A., Tomiya, A. & Hashimoto, K. _Deep Learning and Physics_ (Springer Singapore, 2023). * Wu, D., Wang, L. & Zhang, P. Solving

statistical mechanics using variational autoregressive networks. _Phys. Rev. Lett._ 122, 080602 (2019). Article  ADS  Google Scholar  * Hibat-Allah, M., Inack, E. M., Wiersema, R., Melko, R.

G. & Carrasquilla, J. F. Variational neural annealing. _Nat. Mach. Intell._ 3, 952 – 961 (2021). Article  Google Scholar  * McNaughton, B., Milošević, M. V., Perali, A. & Pilati, S.

Boosting Monte Carlo simulations of spin glasses using autoregressive neural networks. _Phys. Rev. E_ 101, 053312 (2020). Article  ADS  Google Scholar  * Gabrié, M., Rotskoff, G. M. &

Vanden-Eijnden, E. Adaptive Monte Carlo augmented with normalizing flows. _Proc. Natl Acad. Sci._ 119, e2109420119 (2022). Article  MathSciNet  Google Scholar  * Wu, D., Rossi, R. &

Carleo, G. Unbiased Monte Carlo cluster updates with autoregressive neural networks. _Phys. Rev. Res._ 3, L042024 (2021). Article  Google Scholar  * Pan, F., Zhou, P., Zhou, H.-J. &

Zhang, P. Solving statistical mechanics on sparse graphs with feedback-set variational autoregressive networks. _Phys. Rev. E_ 103, 012103 (2021). Article  ADS  MathSciNet  Google Scholar  *

van den Oord, A., Kalchbrenner, N. & Kavukcuoglu, K. Pixel recurrent neural networks. In _Proceedings of The 33rd International Conference on Machine Learning_, 48, 1747–1756 (2016). *

Hibat-Allah, M., Ganahl, M., Hayward, L. E., Melko, R. G. & Carrasquilla, J. Recurrent neural network wave functions. _Phys. Rev. Res._ 2, 023358 (2020). Article  Google Scholar  * Dai,

H., Khalil, E. B., Zhang, Y., Dilkina, B. & Song, L. Learning combinatorial optimization algorithms over graphs. In _Proceedings of the 31st International Conference on Neural

Information Processing Systems_, NIPS’17, 6351–6361 (2017). * Li, Z., Chen, Q. & Koltun, V. Combinatorial optimization with graph convolutional networks and guided tree search. In

_Neural Information Processing Systems_ (2018). * Gasse, M., Chetelat, D., Ferroni, N., Charlin, L. & Lodi, A. Exact combinatorial optimization with graph convolutional neural networks.

In _Neural Information Processing Systems_ (2019). * Joshi, C. K., Laurent, T. & Bresson, X. An efficient graph convolutional network technique for the travelling salesman problem.

Preprint at _arXiv_ https://doi.org/10.48550/arXiv.1906.01227 (2019). * Speck, D., Biedenkapp, A., Hutter, F., Mattmüller, R. & Lindauer, M. T. Learning heuristic selection with dynamic

algorithm configuration. _Proceedings of the International Conference on Automated Planning and Scheduling_ 31, 597–605 (2021). * Schuetz, M. J. A., Brubaker, J. K. & Katzgraber, H. G.

Combinatorial optimization with physics-inspired graph neural networks. _Nat. Mach. Intell._ 4, 367–377 (2021). Article  Google Scholar  * Schuetz, M. J. A., Brubaker, J. K., Zhu, Z. &

Katzgraber, H. G. Graph coloring with physics-inspired graph neural networks. _Phys. Rev. Res._ 4, 043131 (2022). Article  Google Scholar  * Larochelle, H. & Murray, I. The neural

autoregressive distribution estimator. _J. Mach. Learn. Res._ 15, 29–37 (2011). Google Scholar  * Gregor, K., Danihelka, I., Mnih, A., Blundell, C. & Wierstra, D. Deep autoregressive

networks. In _Proceedings of the 31st International Conference on Machine Learning_, 32 of _Proceedings of Machine Learning Research_, 1242–1250

https://proceedings.mlr.press/v32/gregor14.html (PMLR, 2014). * Germain, M., Gregor, K., Murray, I. & Larochelle, H. Made: Masked autoencoder for distribution estimation. In _Proceedings

of the 32nd International Conference on Machine Learning_, 37 of _Proceedings of Machine Learning Research_, 881–889 https://proceedings.mlr.press/v37/germain15.html (PMLR, 2015). * Uria,

B., Côté, M., Gregor, K., Murray, I. & Larochelle, H. Neural autoregressive distribution estimation. _J. Mach. Learn. Res._ 17, 7184–7220 (2016). * Inack, E. M., Morawetz, S. &

Melko, R. G. Neural annealing and visualization of autoregressive neural networks in the Newman-Moore model. _Condens. Matter_ 7, 38–52 (2022). * Ciarella, S., Trinquier, J., Weigt, M. &

Zamponi, F. Machine-learning-assisted Monte Carlo fails at sampling computationally hard problems. _Mach. Learn._ 4, 010501 (2023). Google Scholar  * Kirkpatrick, S., Gelatt, C. D. &

Vecchi, A. Optimization by simulated annealing. _Science_ 220, 671–680 (1983). Article  ADS  MathSciNet  Google Scholar  * Hamze, F., Raymond, J., Pattison, C. A., Biswas, K. &

Katzgraber, H. G. Wishart planted ensemble: a tunably rugged pairwise ising model with a first-order phase transition. _Phys. Rev. E_ 101, 052102 (2020). Article  ADS  MathSciNet  Google

Scholar  * Hammond, D. K., Vandergheynst, P. & Gribonval, R. Wavelets on graphs via spectral graph theory. _Appl. Comput. Harmonic Anal._ 30, 129–150 (2011). Article  MathSciNet  Google

Scholar  * Defferrard, M., Bresson, X. & Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. _Adv. Neural Inf. Process. Syst._ 29, 3844–3852

(2016). * Kipf, T. N. & Welling, M. Semi-supervised classification with graph convolutional networks. _Int. Conf. Learn. Represent._ 4, 2713–2726 (2017). * Andrew, L. Ising formulations

of many np problems. _Front. Phys._ 2, 5 (2014). Google Scholar  * Boettcher, S. Inability of a graph neural network heuristic to outperform greedy algorithms in solving combinatorial

optimization problems. _Nat. Mach. Intell._ https://doi.org/10.1088/0305-4470/15/10/028 (2022). * Angelini, M. C. & Ricci-Tersenghi, F. Modern graph neural networks do worse than

classical greedy algorithms in solving combinatorial optimization problems like maximum independent set. _Nat. Mach. Intell._ https://doi.org/10.1038/s42256-022-00589-y (2022). * Mills, K.,

Ronagh, P. & Tamblyn, I. Finding the ground state of spin Hamiltonians with reinforcement learning. _Nat. Mach. Intell._ 2, 509 – 517 (2020). Article  Google Scholar  * Fan, C. et al.

Searching for spin glass ground states through deep reinforcement learning. _Nat. Commun._ 14, 725–737 (2023). * Mohseni, N., McMahon, P. L. & Byrnes, T. Ising machines as hardware

solvers of combinatorial optimization problems. _Nat. Rev. Phys._ 4, 363 – 379 (2022). Article  Google Scholar  * Tiunov, E., Ulanov, A. & Lvovsky, A. Annealing by simulating the

coherent ising machine. _Opt. Express_ 27, 10288–10295 (2019). Article  ADS  Google Scholar  * King, A. D., Bernoudy, W., King, J., Berkley, A. J. & Lanting, T. Emulating the coherent

ising machine with a mean-field algorithm. https://doi.org/10.48550/arXiv.1806.08422 (2018). * Goto, H. et al. High-performance combinatorial optimization based on classical mechanics. _Sci.

Adv._ 7, eabe7953 (2021). Article  ADS  Google Scholar  * Oshiyama, H. & Ohzeki, M. Benchmark of quantum-inspired heuristic solvers for quadratic unconstrained binary optimization.

_Sci. Rep._ https://doi.org/10.1038/s41598-022-06070-5 (2022). * Barahona, F. On the computational complexity of Ising spin glass models. _J. Phys. A_ 15, 3241 (1982). Article  ADS 

MathSciNet  Google Scholar  * Barbier, J., Krzakala, F., Zdeborová, L. & Zhang, P. The hard-core model on random graphs revisited. _J. Phys._ 473, 012021 (2013). Google Scholar  *

Coja-Oghlan, A. & Efthymiou, C. On independent sets in random graphs. _Random Struct. Algorithms_ 47, 436–486 (2015). Article  MathSciNet  Google Scholar  * Gilmer, J., Schoenholz, S.

S., Riley, P. F., Vinyals, O. & Dahl, G. E. Neural message passing for quantum chemistry. In _Proceedings of the 34th International Conference on Machine Learning - Volume 70_, ICML,

1263–1272 (JMLR, 2017). * Sherrington, D. & Kirkpatrick, S. Solvable model of a spin-glass. _Phys. Rev. Lett._ 35, 1792–1796 (1975). Article  ADS  Google Scholar  * Swendsen, R. H. &

Wang, J.-S. Replica monte carlo simulation of spin-glasses. _Phys. Rev. Lett._ 57, 2607–2609 (1986). Article  ADS  MathSciNet  Google Scholar  * Geyer, C. J. Markov chain Monte Carlo

maximum likelihood. https://api.semanticscholar.org/CorpusID:16119249 (1991). * Hukushima, K. & Nemoto, K. Exchange Monte Carlo method and application to spin glass simulations. _J.

Phys. Soc. Jpn._ 65, 1604–1608 (1996). Article  ADS  Google Scholar  * Earl, D. J. & Deem, M. W. Parallel tempering: theory, applications, and new perspectives. _Phys. Chem. Chem. Phys._

7, 3910–3916 (2005). Article  Google Scholar  * Syed, S., Bouchard-Côté, A., Deligiannidis, G. & Doucet, A. Non-reversible parallel tempering: a scalable highly parallel mcmc scheme.

_J. R. Stat. Soc. Ser. B_ 84, 321–350 (2022). Article  MathSciNet  Google Scholar  * Mohseni, M. et al. Nonequilibrium Monte Carlo for unfreezing variables in hard combinatorial

optimization. https://doi.org/10.48550/arXiv.2111.13628 (2021). * Edwards, S. F. & Anderson, P. W. Theory of spin glasses. _J. Phys. F_ 5, 965 (1975). Article  ADS  Google Scholar  *

Goodfellow, I., Bengio, Y. & Courville, A. _Deep Learning_ (MIT Press, 2016). * Bengio, Y., Lodi, A. & Prouvost, A. Machine learning for combinatorial optimization: a methodological

tour d’horizon. _Eur. J. Oper. Res._ 290, 405–421 (2021). Article  MathSciNet  Google Scholar  * Veličković, P. et al. Graph attention networks. _Int. Conf. Learn. Represent._

https://openreview.net/forum?id=rJXMpikCZ (2018). * Hamilton, W., Ying, Z. & Leskovec, J. Inductive representation learning on large graphs. _Adv. Neural Inf. Process.

Syst._https://proceedings.neurips.cc/paper_files/paper/2017/file/5dd9db5e033da9c6fb5ba83c7a7ebea9-Paper.pdf (2017). * Chang, S. et al. Dilated recurrent neural networks. _Adv. Neural Inf.

Process. Syst._ https://proceedings.neurips.cc/paper_files/paper/2017/file/32bb90e8976aab5298d5da10fe66f21d-Paper.pdf (2017). * Weir, M. D., Hass, J. & Giordano, F. R. _Thomas’ Calculus_

(Pearson Education India, 2005). * Banner, A. _The Calculus Lifesaver: All the Tools You Need to Excel at Calculus_ (Princeton University Press, 2007). * Panchenko, D. The

Sherrington-Kirkpatrick model: an overview. _J. Stat. Phys._ 149, 362–383 (2012). Article  ADS  MathSciNet  Google Scholar  * Panchenko, D. _The Sherrington-Kirkpatrick Model_ (Springer New

York, 2013). Download references ACKNOWLEDGEMENTS We thank Pan Zhang for helpful discussions on the manuscript. This work is supported by Project 61972413 (Z.M.) of the National Natural

Science Foundation of China. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Henan Key Laboratory of Network Cryptography Technology, Zhengzhou, 450001, China Qunlong Ma, Zhi Ma, Jinlong Xu 

& Ming Gao * Department of Algorithm, TuringQ Co., Ltd., Shanghai, 200240, China Hairui Zhang Authors * Qunlong Ma View author publications You can also search for this author inPubMed 

Google Scholar * Zhi Ma View author publications You can also search for this author inPubMed Google Scholar * Jinlong Xu View author publications You can also search for this author

inPubMed Google Scholar * Hairui Zhang View author publications You can also search for this author inPubMed Google Scholar * Ming Gao View author publications You can also search for this

author inPubMed Google Scholar CONTRIBUTIONS M.G. conceived and designed the project. Z.M. and M.G. managed the project. Q.M. and H.Z. performed all the numerical calculations and analyzed

the results. M.G., Q.M., Z.M., and J.X. interpreted the results. Q.M. and M.G. wrote the paper. CORRESPONDING AUTHOR Correspondence to Ming Gao. ETHICS DECLARATIONS COMPETING INTERESTS The

authors declare no competing interests. PEER REVIEW PEER REVIEW INFORMATION _Communications Physics_ thanks Thomas Van Vaerenbergh and the other, anonymous, reviewer(s) for their

contribution to the peer review of this work. A peer review file is available. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in

published maps and institutional affiliations. SUPPLEMENTARY INFORMATION PEER REVIEW FILE SUPPLEMENTAL INFORMATION RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a

Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit

to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are

included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and

your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this

licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Ma, Q., Ma, Z., Xu, J. _et al._ Message passing variational

autoregressive network for solving intractable Ising models. _Commun Phys_ 7, 236 (2024). https://doi.org/10.1038/s42005-024-01711-9 Download citation * Received: 22 December 2023 *

Accepted: 21 June 2024 * Published: 14 July 2024 * DOI: https://doi.org/10.1038/s42005-024-01711-9 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this

content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative