Molecular dynamics simulation of film water thickness and properties at different interfaces in partially saturated frozen soil systems

ABSTRACT The film water, with an exceptional capacity to maintain a premelting, liquid-like state even under subzero conditions, provides a potential dynamic conduit for the movement of

water in frozen soils. However, the distinctive structural and dynamic characteristics of film water have not been comprehensively elucidated. In this study, molecular dynamics (MD)

simulations were conducted to examine the freezing of a system containing ice, water, silica, and gas. The simulations revealed that as the temperature approaches the melting point, the

air-water interface tends to possess a thicker layer of unfrozen water, characterized by a higher diffusion coefficient and lower viscosity. In contrast, the film water near the silica-water

interface tends to be thinner and remains relatively unaffected by temperature, with only one twentieth of the diffusion coefficient and nearly 20 times the viscosity observed at the

air-water interface. These distinct characteristics resulted from the varying interactions between water molecules and their immediate surroundings. Consequently, the film water in proximity

of the silica can be assumed to be relatively immobile compared to that of air-water interface. These findings have implications for the study of unsaturated frozen soil systems, in

particular, the importance of considering the film water at the air-water interface in the modeling framework. SIMILAR CONTENT BEING VIEWED BY OTHERS DYNAMIC CONSTITUTIVE MODEL OF FROZEN

SOIL THAT CONSIDERS THE EVOLUTION OF VOLUME FRACTION OF ICE Article Open access 01 December 2020 ANALYSIS OF LIQUID–VAPOR MIXED MIGRATION MECHANISM IN UNSATURATED SOIL BASED ON THE EFFECT OF

TEMPERATURE ON SOIL MICROSTRUCTURE Article Open access 23 November 2023 THE PHYSICS OF FREEZING AND MELTING IN THE PRESENCE OF FLOWS Article 30 September 2024 INTRODUCTION Water is an

exceptionally abundant and essential liquid in nature, facilitating a wide range of critical physical, chemical, and biological processes1,2,3. Although water is composed of simple atoms, it

exhibits complex structures and anomalous behaviors under specific conditions, such as supercooling, interfaces, and confinement2,4,5. Especially, at the interface, it is well acknowledged

that there is a thin layer of disordered film – this phenomenon is referred to as premelting6. Premelting forms a thin, quasi-liquid layer on the surface of a solid due to the interfacial

interactions to minimize interfacial free energy7. This phenomenon can occur at three different types of interfaces: (1) surface melting between a solid and its vapor or gaseous atmosphere,

(2) grain-boundary melting between crystals of the same material, and (3) interfacial melting in contact with foreign solid or liquid8. For the purpose of consistency, quasi-liquid layers at

various interfaces are collectively referred to as “film water” in this study. Premelting in frozen soil has significant implications for various environmental problems in cold regions,

such as frost heave8. Specifically, under unsaturated condition, when the frozen soil contains solid particles, water, ice and air, all three types of interfaces present. To maintain

consistency, the term ‘film water’ in this study refers to the water layer attached to the surface, regardless of the surface material. Film water properties are fundamentally related to its

thickness, as it measures the spatial extent of the film water layer where the chemical reactions and exchange processes are promoted9. The film water thickness undergoes changes with

temperature and diverges as it approaches the melting point8. Nevertheless, a consensus regarding the estimated thickness of the liquid-like layer has not been reached, owing to

discrepancies among various methods such as experimental techniques, numerical simulations and theoretical approaches10. Various experimental methods have been employed to detect the thin

film thickness on ice surfaces, including X-ray diffraction11, ellipsometry12, atomic force microscopy (AFM)13,14, and spectroscopy15,16. Interfacial melting of ice on foreign substrate,

such as silica, can be challenging to investigate, therefore, has been only studied by indirect methods such as NMR17. These measurements typically cover an extent range from 1 to 100 nm.

Molecular dynamics (MD) simulations are also widely used to assess the thickness of film water. Conde et al. (2008) estimated the film water thickness on free ice surfaces to be within 1 nm

with 2 types of water models and 2 types of ice surfaces, and the separation between film water and ice was based on structural arrangement18. Similarly, Gladich et al. (2011) obtained

comparable film water thickness using a different water model, and the separation also considered the dynamic properties19. At the interface between silica and ice, where the silica surfaces

are either amorphous or crystalline, the thickness of the water film was found to be up to 1.1 nm20. Besides MD simulations, Dash et al. (2006) applied a theoretical thermodynamic solution,

and the determined film water thickness can be up to 2 nm8. Both molecular dynamics (MD) simulations and theoretical predictions yielded remarkedly lower results compared to the laboratory

data. This discrepancy can be partially attributed to the fact that MD and theoretical studies assume ideal conditions and pure systems, while the ice surface is sensitive to perturbations

and impurities encountered in the laboratory experiments, as discussed by Mitsui and Aoki (2019)21. In addition, the variation in MD simulations can be attributed to the chosen water models

and exposed surface of ice, and the methods to identify film water. Laboratory data displayed the most substantial variability, especially when different techniques were employed. That is

mainly because distinct physical quantities are measured to determine the film water thickness using different experimental techniques as it is not directly observable, and another reason is

that techniques such as AFM can affect the tested sample22. The mobility of film water is also important, for example, in permafrost, as it measures the ability of this unique water layer

to serve as a potential channel for mass transport and ice growth in cold regions23,24. Viscosity can be the most critical parameter in water dynamic, which is also closely related to the

diffusion coefficient25. However, determining the dynamic properties of film water experimentally can be challenging, due to the microscale of film water and the need for precise laboratory

conditions26. Molecular dynamics (MD) simulations prove to be a useful tool for probing molecular-level phenomena, thus facilitating an in-depth understanding of thin water films. Kling et

al. (2018) found that diffusion coefficient in film water was considerably small at low temperatures, resembling the behavior of amorphous materials22. Pfalzgraff et al. (2011) investigated

various ice planes exposed to vapor, including basal, prismatic, and pyramidal facets, and figured out that the diffusion coefficient is intrinsically connected to the ice morphology27.

Moreover, Gladich et al. (2011) revealed diffusion coefficient anisotropy at lower temperatures (less than 250 K) as film water resembles the structure of ice, but this anisotropy gradually

smears when temperature increases as the structure shifts towards that of water19. Molecular dynamics (MD) studies have also explored the water behavior near the silica surface28,29. These

studies all either focus on ice-air/vacuum interfaces or water-silica interactions, while very few study investigates specific interaction between silica and ice, and even fewer consider the

influence of gas at the same time. In the context of cryosphere hydrological models at the continuum scale, the components of water (such as capillary water and film water) are crucial for

representing the freeze-thaw characteristics of porous media and determining the soil’s hydraulic properties30. This water retention ability in porous media can be described by the soil

freezing characteristic curve (SFCC), which illustrates the relationship between subzero temperatures and unfrozen water content31. In SFCC, it is commonly assumed that soil water is

retained by capillary forces32. Consequently, film water has not been systematically considered in permafrost models. While some models simply do not include film water32,33, other models

with film water in the framework have dynamic properties (e.g., viscosity) assumed to be similar to capillary water or defined arbitrarily34. However, film water becomes dominant at lower

temperatures, as it is typically more resistant to freezing35. Therefore, it is essential to incorporate film water into permafrost models to improve their accuracy and predictive

capabilities. As for film water properties, the characteristics of film water at interfaces differ significantly from those of bulk water, which has been realized36, but not systematically

investigated. Film water may exhibit heterogeneity and anisotropy in its properties27 due to the influences of different interfaces such as water-air and water-minerals and symmetry breaking

the configuration. However, the influences of interfaces on water flow remain unclear, and thus have not been collectively considered in the study of permafrost system. Furthermore,

previous investigations have often examined the diffusion coefficient (_D_) over a broad temperature range, including temperatures as low as − 40 K below the melting point, with coarse

resolution (typically with an interval of 10 K)19. However, in the study of natural frozen soils, it is practically important to consider temperatures within 10 K below the melting point,

and the evolution of 1 K could induce significant changes. In order to bridge these research gaps, the present study utilizes MD simulations to investigate key parameters associated with the

film water, including the thickness of the water film and its dynamic properties (diffusion coefficient _D_, and viscosity). The study places particular emphasis on temperatures close to

the melting point, subjecting this range to a higher resolution (1 K) analysis. We consider two main types of interfaces in the frozen soil system: the air-ice interface, where a thin layer

of water exists on the ice surface and in contact with air, and the soil-ice interface, where water is absorbed onto the soil particle surface and also constrained by ice. These are

differentiated as “film water” at the silica-water (SW) interface and “film water” at the air-water (AW) interface. By doing so, the study aims to draw parallels to the characteristics

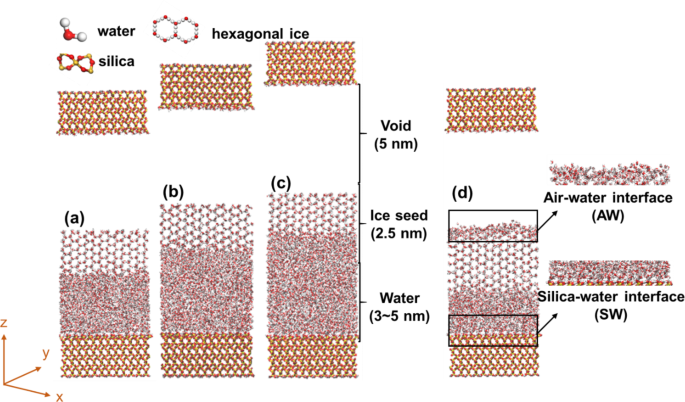
observed in unsaturated frozen soil systems. METHODS MD SIMULATION The initial model configuration, with air, silica, ice, and water coexisting, is depicted in Fig. 1. Silica is suited to

act as a representative of soils in studies examining water-soil interactions, given its status as the most abundant component in soils37. This configuration is achieved through the

coexistence technique38, where each layer of material was placed in direct contact with one another. Within the system, the 5 nm void between the ice and the top silica slab was established

to simulate the gas phase, which was widely adopted by the MD investigations on the premelting of the free ice surface22,27. The silica utilized in this study was represented by the most

stable form found in soils—α-quartz, with the thermodynamically dominant exposed planes (001), and was fully saturated by hydroxyl groups, as a common physicochemical reaction in

nature39,40,41. The unit cell parameters of α-quartz adopted in comparison to the experimental data are listed in Table 1. The simulated ice in the system is the widely occurring hexagonal

ice Ih, with the secondary prismatic plane exposed known for its efficient nucleation rate18. The ice serves as a template to facilitate the crystallization process, considering that

homogeneous nucleation would be extremely time-consuming in the MD simulation42. Additionally, a 5 nm vacuum area from the top silica surface to the edge of the simulation domain was

included to eliminate unwanted interactions across the boundaries. Distances between two silica slabs were varied to test the effect of pore size, which was achieved by applying water layers

of different thicknesses while maintaining the constant 5 nm vacuum area, namely constant gas volume. Specifically, the water layer thickness varied from 3 to 5 nm with the cases labeled as

“siw3,” “siw4,” and “siw5” (Fig. 1a–c). The pore size effect in this study accounts for the joint changes in both the number of water molecules and the interaction distances between water

and silica particles, which are associated with changes in water layer thickness. The unit cell size of the simulation box is 5.88 nm along the x-axis and 4.90 nm along the y-axis. The

z-axis lengths are dependent on the system size. Detailed information regarding the length of z direction of simulation box and the number of molecules in each system is provided in Table 2.

Based on these configurations, the process of water phase change against the silica slab was simulated. To simulate the interaction between water and silica at low temperatures, the

TIP4P/Ice water model43 was utilized in combination with CLAYFF model44. The detailed information of TIP4P/Ice water model and CLAYFF model has been added in the Supporting Information (S1).

During the simulation, all atoms in the silica slab were held fixed, with the exception of -OH groups on the surface. This setting allows the -OH groups to vibrate, imparting the motion

necessary for important physical-chemical processes on the solid surface, while eliminating the risk of slab collapse45. The OH groups are free to move but a constant bond length of 0.1 nm

is maintained, as specified by the CLAYFF force field46. These settings follows the methodology employed in previous studies46,47. The MD simulations were conducted using the open-source

software GROMACS-2021.4 (https://www.gromacs.org/)50. The Newton’s equations of motion are integrated using the leap-frog algorithm, employing a timestep of 2 fs. The NVT ensemble was

applied to keep constant temperature and volume of the system during the simulation. Temperature control was achieved by employing the Nosé-Hoover thermostat with a relaxation time of 1

ps51,52. Periodic boundary conditions (PBC) were implemented in all three spatial dimensions to simulate a parallelly infinite system. To enhance the simulation efficiency, the short-range

interactions and the real part of the long-range interactions were truncated at a distance of 1.2 nm. Long-range interactions beyond this cutoff range were computed using the

three-dimensional particle mesh Ewald summation (PME) package53. The LINCS algorithm was used to maintain the length of the water hydrogen bond constant54. Higher temperatures compared to a

previous study (−40 ℃)19, ranging within 10 K below the melting temperature, were set with an interval of 1 K to generate different simulation cases. Note that this temperature range is of

particular interest for the study for permafrost in nature, as this is a critical temperature range where the water behavior undergoes substantial transformations. Moreover, within this

temperature range, the diffusion coefficient is less influenced by the ice morphology and exhibits isotropic behavior, as highlighted by Gladich et al. (2011)19. As the melting temperature

is subject to the system size (represented by the total water content in this study), the simulation results of systems with different sizes were presented over different temperature ranges.

The lower temperature thresholds for all systems were uniformly established at a frozen temperature of 255 K, whereas the upper temperature boundaries were chosen to be precisely 1 K below

the respective critical points for each distinct system. The melting points of water for all simulation cases were determined using the potential energy method, following the approach

described by Conde et al. (2017)55, and the detailed information regarding this process can be found in the Supporting Information (S2). For all the simulations with different seeds, only

the frozen cases were considered for further analysis, as in melted cases the phenomenon of premelting disappear. ANALYSIS OF FILM WATER PROPERTIES FILM WATER THICKNESS The method of

identifying the liquid-like water molecules from the ice crystal is vital in determination of film water thickness. In previous studies, the order parameter _qt_ was utilized to determine

the quantity of molecules exhibiting liquid-like properties18,19. The order parameter _qt_ distinguishes unfrozen water from ice based on their distinct structures, as water molecules are

randomly distributed, while ice crystals are characterized by the tetrahedral structure. However, as water undergoes supercooling, it also becomes increasingly tetrahedral56. Besides, the

choice of the _qt_ varies across different water models and can be subjective19. Consequently, it is challenging in accurately distinguishing between ice and liquid-like molecules, and this

could result in an inaccurate estimation of the thickness of the water film. The Chill+ algorithm used in this study identifies the state of water molecules based on the correlation of

orientational order with its four closest neighbors57. This Chill+ algorithm is open-source and has been integrated into the visualization software Ovito. By determining the number of

unfrozen water molecules, it is possible to calculate the thickness of the water film using Eq. (1)18: $$\xi =\frac{{N}_{l}M}{\rho {N}_{A}{L}_{x}{L}_{y}}$$ (1) where \(\xi\) represents the

thickness of the film water, \({N}_{l}\) denotes the number of unfrozen water molecules at equilibrium, _M_ represents the molecular weight of water (18.02 g/mol), \({N}_{A}\) is Avogadro’s

number, the product of \({L}_{x}\) and \({L}_{y}\) represents the area of the interface, and ρ denotes the density of liquid water. IN-PLANE DIFFUSION COEFFICIENT The transition of ice from

a solid to a liquid state has been observed to occur through a two-dimensional phase-transition process, taking place layer by layer58,59. As the PBCs were applied, water diffusion along the

coordinates parallel to the interface (_x_ and _y_) is unbounded. As a result, our attention was directed towards understanding _D_ parallel to the silica slab within the interfacial

region, which corresponds to the thickness of the water film. In the context of bulk fluids, the most employed method for determining diffusion coefficient _D_ is the Einstein relation that

relies on the mean square displacement (MSD)60. However, this approach is not applicable to systems with interfaces or confined fluids. In these cases, molecules within the region of

interest only remain for a limited time before entering other regions, and the asymmetry of the interface introduces unique characteristics in interfacial self-diffusion. To address this,

Liu et al. (2004) proposed a method that enforces virtual boundary conditions on the molecular system, enabling the layering of the system in specific regions of interest61. For calculation

of layer-specific _D_, a layer with boundaries _{l_,_ h}_ was assumed, and the MSD within this range in one-dimension (e.g., x-direction) can be expressed as: $${ \langle \varDelta

{x}^{2}({\uptau },{\updelta }) \rangle }_{\{l,h\}}=\frac{1}{{N}_{{\uptau }}}\sum _{\delta =1}^{{N}_{{\uptau }}}\left(\frac{1}{{N}_{p}\left(\delta , \delta +\tau \right)}\sum _{n=1}^{n\in

\zeta (\delta , \delta +{\uptau })}{\left|\overrightarrow{{x}_{n}\left(\delta +{\uptau }\right)}-\overrightarrow{{x}_{n}\left(\delta \right)}\right|}^{2}\right)$$ (2) where the set _ζ(δ_,_ δ

 + τ)_ represents all the particles that remain within the layer during the time interval between _δ_ and _δ + τ_, \({N}_{p}\left(\delta , \delta +\tau \right)\) denotes the number of

particles in this set. It is crucial to mention that only the molecules that remain within the studied regions are taken into account. By doing so, it becomes possible to calculate the

interfacial _D_ by obtaining survival probabilities within these regions, which is determined by Eq. (3): $$P\left({\uptau }\right)=\frac{1}{T}\sum _{\delta =1}^{T}\frac{N\left(\delta

,\delta +{\uptau } \right)}{N\left(\delta \right)}$$ (3) Hence, we can derive the expression for the one-dimensional _D__xx_: $${D}_{xx}\left(\left\{l,h\right\}\right)=\underset{{\uptau }\to

{\infty }}{\text{lim}}\frac{{\langle \varDelta {x}^{2}\left({\uptau }\right) \rangle }_{\{a,b\}}}{2P\left({\uptau }\right)}$$ (4) Based on the same method, _D__yy_ can be calculated, and

then the parallel diffusion coefficient _D__xy_ can be obtained by: $${D}_{xy}\left(\left\{l,h\right\}\right)=\frac{{D}_{xx}+{D}_{yy}}{2}$$ (5) During the calculation, the virtual boundaries

were determined by the thickness of film water. The TIP4P-Ice water model has a known problem of underestimating the diffusion coefficient by nearly 2 times62. Consequently, the

determination of _D_ for film water may be significantly lower than the actual value for bulk water due to the specific water model employed. Therefore, in order to analyze the trend of _D_

in film water, the estimated _D_ will be compared to the bulk value obtained using the same water model, rather than the real value for water. The calculated _D_ of bulk water using the

TIP4P-Ice model, obtained using the same method employed to determine the in-plane diffusion coefficient, is 2.00 × 10−6 cm2/s at 260 K. This value deviates from the reported value of 2.15 ×

 10−6 cm2/s for bulk water applying TIP4P/Ice63 by only 7%, demonstrating the reliability of this method for determining the diffusion coefficient. Furthermore, a series of bulk diffusion

coefficients of pure water was simulated to enable comparisons with the local _D_ at the same temperature ranges. VISCOSITY The viscosity and diffusion coefficient are interrelated, as

proposed by Louden and Gezelter (2018) and mathematically expressed by Eq. (6)25: $${\eta }_{s}=\frac{{D}_{bulk}}{{D}_{s}}{\eta }_{bulk}$$ (6) where \({\eta }_{s}\) and \({\eta }_{bulk}\)

represent viscosity in film water layer and bulk water, respectively, \({D}_{s}\)and \({D}_{bulk}\) represent diffusion coefficient in the film water layer and bulk water, respectively.

Notably, the viscosity of TIP4P-Ice water model is different from the actual water as well. Therefore, the viscosity of bulk water predicted by TIP4P-Ice water model64 was selected for the

calculation of film water viscosity. RESULTS THICKNESS OF FILM WATER LAYER The variation of film water thickness with temperature differs at the two different interfaces for systems of

various sizes according to Fig. 2a. For all the systems, the film water thickness at the air-water interface (AW) is highly dependent on temperature, as an increase in temperature leads to a

substantial thickening in the unfrozen water layer, and the increase rate also rises with temperature. When the temperature approaches the melting point, the thickness of the water film at

the AW increases by up to 154.8–224% compared to that at 255 K. Conversely, the film water thickness at the silica-water interface (SW) appears to be unaffected by temperature variations,

maintaining a value of approximately 0.5 nm. Notably, at the lowest selected temperature of 255 K, the film water thickness at the AW interface is observed to be even marginally thinner than

that at the silica-water (SW) interface. This reaffirms the strong temperature dependence of film water associated with the air interface, in contrast to the relative insensitivity of SW

interface film water to temperature changes. This finding indicates that different interfaces can have distinct impacts on the freezing process. Pore size effect was also observed in the

film water thickness among different systems (Fig. 2a). The thickness of the film water layer connecting to air is subject to influence of the system size, as siw4 and siw5 exhibit thicker

film water layers than siw3, which can also be observed for the layer at the silica side, but to a much less extent. At the AW interface, the influence of pore size contributes to an

increase of 5–45% in the film water thickness from siw3 to siw4 at temperature increases from 255 K to 263 K. The subsequent increase from siw4 to siw5 is relatively moderate, ranging from 1

to 13%. The diminishing rate of increase in the water film thickness as pore size further expands indicates a decreasing influence of pore size on the film thickness, suggesting a

transition towards a nearly size-independent behavior in further larger pores. In contrast, at the SW interface, the impact of pore size results in increases of less than 15% across all

cases. The effects of pore size have been noted in Fig. 2a. These trends in film water thickness can be related to the change in melting point due to the pore size effect. It was observed

that as the pore size increases, the melting point decreases (see Supporting Information S2, Fig. S1), which corresponds to an increase in film water thickness. Systems of varying sizes

require different amounts of time to equilibrate. Figure 2b–d demonstrates the determined water film thickness at two consecutive time intervals. Based on Fig. 2b, it can be observed that in

the smaller siw3 case, the film water thicknesses calculated at 50 ns show minimal variation (within 10%) when compared to those at 40 ns, across different temperatures. This finding

implies that the MD simulation for the siw3 system has reached equilibrium after 50 ns. Similar equilibrium has not been observed until at 80 ns for the larger siw4 case (Fig. 2c), and at

140 ns for the largest siw5 case (Fig. 2d). Film water at the SW interface generally shows less variation compared to that at the AW interface, as indicated by the error bar, which

demonstrates the stability of film water at the SW interface. When approaching the melting point, this variation could become larger, as seen in the siw5 case. In summary, the presence of

water at the air-water (AW) interface (i.e., film water layer between ice and air) is influenced by both the temperature and pore size, and temperature plays a dominant role in thickening

the film water layer. However, film water at the SW interface is much less affected compared to that at the AW interface. DYNAMIC PROPERTIES OF FILM WATER LAYER The average lateral diffusion

coefficients (_D_) within the film water layer vary at the two different interfaces in all systems, as shown in Fig. 3a. The specific ranges of _D_ for AW and SW at different systems are

detailed in Table 3. The average lateral diffusion coefficients of film water are generally lower than those of bulk water (indicated by the dashed line). Lower temperature, such as 255 K in

siw3, results in an in-plane diffusion coefficient nearly two magnitudes lower than that of bulk water for AW. The much lower _D_ is also found in the film water layer at the SW interface

for all the cases with all the temperatures. However, as the temperature increases towards the melting point, the lateral _D_ of film water near the AW interface approaches that of bulk

water. The lateral _D_ of water molecules at the SW interface remains relatively constant regardless of temperature and pore size compared to that at the AW interface, similar to what is

found in the film water thickness. For the small system siw3, the lateral _D_ of film water at AW interface shows a substantial increase as the temperature rises from 255 K to 264 K, by

approximately two orders of magnitude. For larger cases siw4 and siw5, significant increases of 23 and 13 times are observed as the temperature approaches the melting point (262 K and 261 

K), respectively. These findings clearly indicate that the diffusion coefficient at the AW interface is highly dependent on temperature. The error bars represent variations among simulations

with different seeds, which become significant particularly at temperatures near the melting point; note this is clearer with a normal scale along the vertical axis than the log scale here.

The increase in pore size from siw3 to siw4 contributes to an average 1.3-fold increase in lateral _D_ of film water at the AW interface. However, there is an insignificant increase in _D_

from siw4 to siw5. This phenomenon can be attributed to the diminishing impact of pore size as it increases further, indicating that there could be an upper limit for local _D_ with

increasing size prior to reaching the melting temperature. The difference between film water _D_ at different interfaces is represented by the ratio of _D_ at the SW to AW interface (refer

to Fig. 3b). When the temperature is as low as 255 K, siw3 has even lower lateral _D_ of film water at AW than SW. As the temperature rises, _D_ in the AW film water layer increases,

surpassing that of SW film water. At 259 K, the ratio of film water _D_ at the SW to AW interface is approximately 35% in siw3, while at 264 K, this ratio becomes less than 5%. For larger

systems, the differences of film water _D_ between the SW and AW interfaces are relatively small in siw4 and siw5 at low temperatures 255 K. As the temperature approaches the melting point,

the differences enlarge with the ratio of _D_ at SW to AW interface down to approximately 5% for siw4, and even lower for siw5. The general trends agree well with that obtained by Gladich et

al. (2011) (lateral _D_ on the free ice surface)19 and Carignano et al. (2005) (_D_ of bulk water)65, where the diffusion coefficient of film water at free ice surface is observed to be

lower than that of bulk water and always increases with temperature. Data from Gladich et al. (2011) span within a temperature range from 230 to 290 K with a 10 K interval. To facilitate

comparison with our data (255–264 K), we fitted Gladich et al.‘s data to obtain D values at 255–265 K with a 1 K interval. The D values computed by Gladich et al. (2011) at 261 K are very

close to those of siw5 and siw4 at the AW interface in the present study, with a deviation of only 17.51% (Fig. 3a). However, the discrepancy becomes pronounced at temperatures below 261 K,

where the D values determined in this study are notably lower. This discrepancy can be attributed to the different methodologies employed for calculating the local diffusion coefficient. In

the study of Gladich et al. (2011), the in-plane diffusion coefficient of film water is assumed to be proportionable to the bulk system, and the number reported is scaled according to the

volume fraction of film water within a fixed domain. The approach adopted in the present study directly calculates the local diffusion coefficient. Our findings reveal that the film water at

the SW interface exhibits limited mobility with increasing temperature and pore size, indicating a more restrained water molecular environment. In contrast, the film water at the AW

interface demonstrates enhanced mobility, particularly as the temperature is lower than the melting point. VISCOSITY We calculated the viscosity of film water at different interfaces based

on the diffusion coefficient data, as shown in Fig. 4. The viscosity profile mirrors that of the local diffusion coefficient, albeit in an inverse relationship according to Eq. (6).

Specifically, across the three systems examined, viscosities of film water at the AW interface are notably high at low temperatures, declining progressively as temperatures increases, and

eventually converge towards the bulk water viscosity as the temperatures rise to the melting point. In contrast, for the SW interface, the average film water viscosities across systems were

significantly elevated, with an average of 237.68 mPa·s—this is approximately 32 times greater than the bulk water value of the TIP4P-Ice water model (7.2 mPa·s). Besides, these high

viscosities remain largely invariant over the simulated temperature range. A higher viscosity indicates a reduced fluid dynamics rate. Therefore, the water film present on the soil surface

can be considered as being relatively immobile, while that on the free ice surface is more dynamic depending on the temperature. DISCUSSION FILM WATER BEHAVIORS AT TWO INTERFACES The density

profile of oxygen atoms in film water were analyzed to learn more about the layer-specific structural properties (Fig. 5). Using the siw4 system as an example, with the z direction

perpendicular to the ice plane and assuming the lower silica end as the starting point, it was observed that the density at SW interface (as high as 1400 kg/cm3, indicated by yellow dashed

box) is higher than that of bulk water (1000 kg/m3), while density at AW interface (indicated by red dashed box) is always lower. Additionally, the density of film water at the AW interface

is more responsive to temperature changes, displaying a decrease with increasing temperature. In contrast, the density at the SW interface remains relatively unaffected by temperature

variations. The properties of film water at different interfaces have been examined from various dimensions, including film thickness, dynamic properties, and density profiles. The distinct

behaviors of film water at these interfaces in response to temperature can be attributed to the unique bonding interactions between water molecules and their neighboring surfaces. For film

water at the SW interface, the OH groups on the silica surface exhibit strong affinity for water molecules, leading to changes in their distribution and orientation, facilitated the hydrogen

bonding between them20,66. This interaction promotes the formation of hydration layers—a more ordered and dense arrangement of water molecules on the edge surfaces of silica. The effect of

the strong interactions extends to a certain spatial extent, maintaining a stable film thickness even at higher temperatures (still below the melting point) and resisting freezing at low

temperatures. Consequently, water molecules near the SW interface form a solid-like, relatively constant layer that is distinct from ice. The dense structure induced by these interactions

result in lower mobility compared to bulk water. This phenomenon is not limited to systems containing ice but is also observed in configurations consisting of silica and water, where

interfacial water exhibits higher density and slower displacement compared to bulk water67. Therefore, the structural and dynamic properties of the film water layer at the SW interface are

relatively insensitive to changes in temperature. Extensively, we speculate for film water in contact with a hydrophilic foreign material, the water molecules are strongly attracted and

remain relatively stable, forming a solid-like structure with reduced mobility. The formation of film water at the AW interface has been a long-debated topic, as systematically reviewed by

Sun et al. (2023)68. One prominent theory is the molecular undercoordination theory, which points out that surface molecules are inherently unstable due to the lack of neighboring molecules

above, prompting the formation of a liquid phase. According to our simulation results, the film of water observed at the AW interface was generated by simulating initially intact ice at

temperatures even well below the melting point. Despite these low temperatures, the film of water remains unfrozen even at equilibrium. This observation supports the molecular

undercoordination theory. Therefore, the film water at the AW interface is formed by weak bonding interactions at the free ice surface, while the state of ice is highly sensitive to

temperature. As the temperature increases, the ice melts accordingly, leading to the increase in the film water thickness at the AW interface. This results in a higher diffusion coefficient

of the film water at this interface. LIMITATION AND IMPLICATION OF THIS STUDY Although this study discovers distinct film water behavior at different interfaces in the unsaturated frozen

soil systems, we recognize that there are aspects that could benefit from additional investigation. First, the availability of data for validation is limited, and thus the results in this

study are validated indirectly. As discussed in section “Introduction”, there are significant differences (up to two orders of magnitude) in film water thickness measurements among various

techniques, and most of these studies focus on film water at the AW interface. Consequently, it is challenging to directly validate the estimated film water thickness based on data from

previous studies using different techniques. As for molecular dynamics (MD) simulations, previous results vary according to the force field, boundary or initial conditions, and those

conditions are not identical to this study. Overall, we have only compared the general trends rather than exact numbers in the film water thickness. For the diffusion coefficient _D_, we

first compared the _D_ of a pure water system from this study with that reported in a previous study also using TIP4P/Ice water model. The good match supports the rational of chosen model

parameter and calculation method of lateral _D_. Additionally, the lateral _D_ of film water was compared with those from previous studies (Gladich et al., 2011; Carignano et al., 2005)

(Fig. 3a), and the trends show good agreement with our results. The discrepancies in precise values can also be attributed to the specific method used to calculate the local diffusion

coefficient (_D_). Our method is more direct and therefore provides a clearer and more accurate representation of the local diffusion behavior. As the melting point is a vital criterion for

evaluating the performance of water models in phase change simulations, we have added simulations of well-studied systems, including fully saturated systems with varying sizes, to estimate

their melting points as a function of pore size (see Supporting Information S3, Figs. S2, S3). The results show consistency with previous work (Findenegg et al., 2008), further validating

our simulation protocol for the freezing-thawing process. In addition, the simulated results align well with the established theoretical framework proposed by previous studies, which further

validates these outcomes, as discussed in section “Discussion”. Second, pore size effects inherently involve changes in both the number of water molecules and the pore size (interactive

distance). These two effects are difficult to separate and tend to work in tandem. Even when the distance between silica slabs is kept constant, the gap thickness (interactive distance) will

vary as the number of water layers increases. In the current cases, we maintained a constant gap thickness, which resulted in variations in the pore size. To decouple the mixed effects due

to pore size changes, we try to investigate this system in another perspective by establishing new configurations with a constant pore size but varied water number and gap thickness. Three

new cases, labeled siw3*, siw4*, and siw5*, are shown in Fig. S4 in the Supporting Information. The calculated film water thickness in the new cases versus temperature and pore size do not

differ significantly from the previous cases when the gap thickness is changed. For the trend in film water thickness, as temperature and pore size increase, the film water thickness at SW

interface remains relatively insensitive, while a more pronounced increase is observed at the AW interface (Fig. S5). Compared to the siw systems, the siw* systems exhibit a deviation in

film water thicknesses of less than 10% at the SW interface and less than 20% at the AW interface (Fig. S6). A detailed discussion is provided in the Supporting Information (S4). Despite the

different settings for the position of the top silica slab in cases with the minimal gap thickness of 5 nm, we observe similar results in the film water thickness. The strong correlation

between film water thickness and the number of water molecules, still, can be attributed to (1) the thickness of water/ice layer and (2) the interaction distance to the bottom slab. These

two factors are strongly coupled in all cases. In summary, the effect of the number of water molecules and pore size is inherently coupled, while the effect of the distant (> = 5 nm) top

slab is not significant. Third, this work intends to investigate the behavior of water in frozen soil and is grounded in the theoretical frameworks of cryosphere hydrology, where film water

is always neglected or simplified. However, the upscaling directly from the molecular scale to the continuum scale and integrating these findings into mathematical models remains a

significant challenge that requires further study. Nonetheless, our research systematically considered film water at two distinct interfaces within a complex system, and provides valuable

insights into the physical models of frozen soil, which are crucial for simulation settings. The system examined in this study closely mirrors unsaturated frozen soil systems. The

traditional REV (representative elementary volume) scale hydrological model neglects the film water present in the unsaturated frozen soil at the AW, while considering only the film water at

the SW interface. The REV scale is the smallest volume of the porous medium that can be considered statistically representative of the entire medium’s properties, which is essential for

linking microscale phenomena to macroscopic behavior and simplifying the analysis of transport processes. This study suggests that film water at the AW can exhibit higher water content and

faster dynamics within the practical temperature range (within 10 K from the melting point). Consequently, it is imperative to include the film water at the AW within the modeling framework

when the unsaturated frozen soil condition is considered. It is noteworthy that the impact of film water is far beyond hydrology. The study of film water is an important subject in chemical

physics and has been a topic of long-standing debate. As discussed in the introduction, relatively little attention has been paid to film water in complex silica-based solid-ice-water-gas

systems. Due to the limitations of techniques that focus on different physical quantities, a consensus regarding the film water properties has not yet been reached. This study aims to

quantitatively measure the film water thickness and dynamic properties, and proposes assumptions for the underlying mechanisms based on the results, thereby contributing to the film water

study. One of the common questions across various fields is the nature and classification of “water” at interfaces, particularly at the SW interface. These unique water layers raise the need

to consider whether this type of “water” should be regarded as a distinct phase or state of water. This is critical, as there is ongoing controversy over whether describing this unique

layer in analogy to the liquid phase is a valid and realistic approach, which is a prerequisite for the afterward property parameterization. From a practical perspective, water exhibits

active reactions and mass transport. _D_ of the film water at the SW interface falls between the estimated values of bulk water and ice (Fig. 3). At the AW interface, the diffusion

coefficient of the film water is nearer to that of bulk water when the temperature is elevated, whereas it approaches that of ice when the temperature decreases. Therefore, the film water at

SW exhibits properties distinct from both bulk water and solid crystals. Based on the abnormal properties of interfacial water, especially the structured and dynamic behavior, this study

suggests that film water at SW interface may not be classified as conventional liquid water, and that at AW should be considered depending on the temperature. CONCLUSION In this study,

molecular dynamics (MD) simulations were conducted to investigate the film water, with a focus on determining its thickness, layer-specific diffusion coefficient and viscosity at the

silica-water (SW) and air-water (AW) interfaces. The results revealed that the film water at the AW interface is influenced by both temperature and pore size, with temperature exerting a

dominant effect. Moreover, the mobility of this layer gets enhanced with rising temperature and pore size. In contrast, the film water at the SW interface remains relatively unaffected by

temperature and pore size. This distinction can be attributed to the underlying mechanisms governing film water at different interfaces. The hydroxylated silica surface imposes strong

attractive forces and forms hydrogen bonds between water molecules and the -OH groups on the silica surface, leading to the formation of a structured, solid-like layer characterized by high

density and low mobility. In contrast, the film water at the AW interface is dependent on the weak bonding of ice and exhibits sensitivity to temperature variations. The abnormal properties

of the water at the silica-water (SW) interface, such as its high density and solid-like structure, suggest that this “water” may not behave like conventional liquid water, which has

significant implications for many engineering and research applications. The system studied in this research bears resemblance to unsaturated frozen soil systems. Our finding is different

from the traditional Representative Elementary Volume (REV) scale models of unsaturated frozen soil, which typically only considers the water at the SW interface. Instead, it suggests that

the film water at the air-water (AW) interface should be considered for a more accurate representation. The findings from this study contribute to enhancing our understanding and predictive

capabilities regarding the behavior of ice and frozen soil in both natural and engineered systems. DATA AVAILABILITY The datasets generated during the current study are available upon

reasonable request from the corresponding author, Prof. Ling Li ([email protected]). REFERENCES * Longuet-Higgins, M. S. Mass transport in water waves. _Philos. Trans. R Soc. Lond. Ser.

Math. Phys. Sci._ 245(903), 535–581 (1953). ADS  MathSciNet  MATH  Google Scholar  * Levinger, N. E. Water in confinement. _Science_ 298(5599), 1722–1723 (2002). Article  CAS  PubMed  MATH

  Google Scholar  * Wiggins, P. M. Role of water in some biological processes. _Microbiol. Rev._ 54(4), 432–449 (1990). Article  CAS  PubMed  PubMed Central  MATH  Google Scholar  *

Björneholm, O. et al. _Water Interfaces Chem. Rev._ 116(13):7698–7726 (2016). PubMed  Google Scholar  * Gallo, P., Loerting, T. & Sciortino, F. Supercooled water: a polymorphic liquid

with a cornucopia of behaviors. _J. Chem. Phys._ 151, 210401 (2019). Article  ADS  CAS  PubMed  Google Scholar  * Wettlaufer, J. S. & GraeWorster, M. Premelting dynamics. _Annu. Rev.

Fluid Mech._ 38, 427–452 (2006). Article  ADS  MathSciNet  MATH  Google Scholar  * Slater, B. & Michaelides, A. Surface premelting of water ice. _Nat. Rev. Chem._ 3(3), 172–188 (2019).

Article  CAS  MATH  Google Scholar  * Dash, J. G., Rempel, A. W. & Wettlaufer, J. S. The physics of premelted ice and its geophysical consequences. _Rev. Mod. Phys._ 78(3), 695–741

(2006). Article  ADS  CAS  MATH  Google Scholar  * Wren, S. N., & Donaldson, D. J.(2011) Exclusion of Nitrate to the Air–Ice Interface During Freezing. _J. Phys. Chem. Lett. _ 2(16),

1967-1971. https://doi.org/10.1021/jz2007484 * Bartels-Rausch, T. et al. A review of air–ice chemical and physical interactions (AICI): liquids, quasi-liquids, and solids in snow. _Atmos.

Chem. Phys._ 14(3), 1587–1633 (2014). Article  ADS  MATH  Google Scholar  * Lied, A., Dosch, H. & Bilgram, J. H. Glancing angle X-ray scattering from single crystal ice surfaces. _Phys.

B Condens. Matter_. 198(1–3), 92–96 (1994). Article  ADS  CAS  Google Scholar  * Furukawa, Y., Yamamoto, M. & Kuroda, T. Ellipsometric study of the transition layer on the surface of an

ice crystal. _J. Cryst. Growth_. 82(4), 665–677 (1987). Article  ADS  CAS  MATH  Google Scholar  * Pittenger, B. et al. Premelting at ice-solid interfaces studied via velocity-dependent

indentation with force microscope tips. _Phys. Rev. B_. 63(13), 134102 (2001). Article  ADS  MATH  Google Scholar  * Peng, J. et al. Water-solid interfaces probed by high-resolution atomic

force microscopy. _Surf. Sci. Rep._ 77 (1), 100549 (2022). Article  CAS  Google Scholar  * Elbaum, M., Lipson, S. G. & Dash, J. G. Optical study of surface melting on ice. _J. Cryst.

Growth_. 129 (3–4), 491–505 (1993). Article  ADS  CAS  MATH  Google Scholar  * Bluhm, H. et al. The premelting of ice studied with photoelectron spectroscopy. _J. Phys. Condens. Matter_. 14,

L227–L233 (2002). Article  CAS  MATH  Google Scholar  * Ishizaki, T. et al. Premelting of ice in porous silica glass. _J. Cryst. Growth_. 163 (4), 455–460 (1996). Article  ADS  CAS  MATH 

Google Scholar  * Conde, M. M., Vega, C. & Patrykiejew, A. The thickness of a liquid layer on the free surface of ice as obtained from computer simulation. _J. Chem. Phys._ 129 (1),

14702 (2008). Article  ADS  CAS  MATH  Google Scholar  * Gladich, I. et al. Arrhenius analysis of anisotropic surface self-diffusion on the prismatic facet of ice. _Phys. Chem. Chem. Phys._

13 (44), 19960–19969 (2011). Article  CAS  PubMed  Google Scholar  * Uchida, S., Fujiwara, K. & Shibahara, M. Structure of the water molecule layer between ice and amorphous/crystalline

surfaces based on molecular dynamics simulations. _J. Phys. Chem. B_. 125 (33), 9601–9609 (2021). Article  CAS  PubMed  MATH  Google Scholar  * Mitsui, T. & Aoki, K. Fluctuation

spectroscopy of surface melting of ice with and without impurities. _Phys. Rev. E_. 99, 010801 (2019). Article  ADS  CAS  PubMed  MATH  Google Scholar  * Kling, T., Kling, F. & Donadio,

D. Structure and dynamics of the quasi-liquid layer at the surface of ice from molecular simulations. _J. Phys. Chem. C_. 122 (43), 24780–24787 (2018). Article  CAS  MATH  Google Scholar  *

Lebeau, M. & Konrad, J. A new capillary and thin film flow model for predicting the hydraulic conductivity of unsaturated porous media. _Water Resour. Res._ 46(12). (2010). * Teng, J. et

al. A mathematic model for the soil freezing characteristic curve: the roles of adsorption and capillarity. _Cold Reg. Sci. Technol._ 181, 103178 (2021). Article  MATH  Google Scholar  *

Louden, P. B. & Gezelter, J. D. Why is ice slippery? Simulations of shear viscosity of the quasi-liquid layer on ice. _J. Phys. Chem. Lett._ 9 (13), 3686–3691 (2018). Article  CAS 

PubMed  MATH  Google Scholar  * Mamontov, E. et al. Dynamics and structure of hydration water on rutile and cassiterite nanopowders studied by quasielastic neutron scattering and molecular

dynamics simulations. _J. Phys. Chem. C_. 111 (11), 4328–4341 (2007). Article  CAS  MATH  Google Scholar  * Pfalzgraff, W., Neshyba, S. & Roeselova, M. Comparative molecular dynamics

study of vapor-exposed basal, prismatic, and pyramidal surfaces of ice. _J. Phys. Chem. A_. 115 (23), 6184–6193 (2011). Article  CAS  PubMed  MATH  Google Scholar  * Kroutil, O. et al.

Computer simulations of quartz (101)–water interface over a range of pH values. _J. Phys. Chem. C_ 2015(119):9274–9286 . * Bistafa, C. et al. Water on hydroxylated silica surfaces: work of

adhesion, interfacial entropy, and droplet wetting. _J. Chem. Phys._ 155 (6), 64703 (2021). Article  CAS  MATH  Google Scholar  * Wan, X. et al. Prediction of the unfrozen water content in

soils based on premelting theory. _J. Hydrol._ 608, 127505 (2022). Article  MATH  Google Scholar  * Ma, T. et al. Soil freezing and soil water retention characteristics: connection and

solute effects. _J. Performa Constr. Facil_. 31, D4015001 (2015). Article  Google Scholar  * Kurylyk, B. L. & Watanabe, K. The mathematical representation of freezing and thawing

processes in variably-saturated, non-deformable soils. _Adv. Water Resour._ 60, 160–177 (2013). Article  ADS  MATH  Google Scholar  * McKenzie, J. M., Voss, C. I. & Siegel, D. I.

Groundwater flow with energy transport and water–ice phase change: Numerical simulations, benchmarks, and application to freezing in peat bogs. _Adv. Water Resour._ 30 (4), 966–983 (2007).

Article  ADS  Google Scholar  * Ming, F. et al. Estimation of hydraulic conductivity of saturated frozen soil from the soil freezing characteristic curve. _Sci. Total Environ._ 698, 134132

(2020). Article  CAS  PubMed  Google Scholar  * Chen, Y. et al. Quantification and division of unfrozen water content during the freezing process and the influence of soil properties by

low-field nuclear magnetic resonance. _J. Hydrol._ 602, 126719 (2021). Article  MATH  Google Scholar  * Lu, N., Luo, S. & Zhou, B. Water adsorption-induced pore-water pressure in soil.

_J. Geotech. Geoenviron Eng._ 148 (6), 4022042 (2022). Article  MATH  Google Scholar  * Etesami, H. et al. _Silicon and nano-silicon in Environmental Stress Management and crop Quality

Improvement: Progress and Prospects_ (Elsevier, 2022). * Conde, M. M. et al. Determining the phase diagram of water from direct coexistence simulations: the phase diagram of the TIP4P/2005

model revisited. _J. Chem. Phys._ 139 (15), 154505 (2013). Article  ADS  CAS  PubMed  MATH  Google Scholar  * Kim, Y. et al. Dissociation of water on a flat, ordered silica surface.

_Langmuir_, 19. (2003). * Murdachaew, G. et al. Dissociation of HCl into ions on wet hydroxylated (0001)-quartz. _J. Phys. Chem. Lett._ 4 (20), 3500–3507 (2013). Article  CAS  MATH  Google

Scholar  * Yang, J. & Wang, E. G. Reaction of water on silica surfaces. _Curr. Opin. Solid State Mater. Sci._ 10, 33–39 (2006). Article  ADS  CAS  MATH  Google Scholar  * Espinosa, J. R.

et al. Homogeneous ice nucleation evaluated for several water models. _J. Chem. Phys._ 141 (18), 18C529 (2014). Article  CAS  PubMed  MATH  Google Scholar  * Abascal, J. L. F. et al. A

potential model for the study of ices and amorphous water: TIP4P/Ice. _J. Chem. Phys._ 122 (23), 234511 (2005). Article  ADS  CAS  PubMed  MATH  Google Scholar  * Cygan, R. T., Liang, J.

& Kalinichev, A. G. Molecular models of hydroxide, oxyhydroxide, and clay phases and the development of a general force field. _J. Phys. Chem. B_. 108 (4), 1255–1266 (2004). Article  CAS

  MATH  Google Scholar  * Zielke, S. A., Bertram, A. K. & Patey, G. N. Simulations of ice nucleation by kaolinite (001) with rigid and flexible surfaces. _J. Phys. Chem._ 120, 1726–1734

(2015). Article  MATH  Google Scholar  * Soni, A. & Patey, G. N. How microscopic features of mineral surfaces critically influence heterogeneous ice nucleation. _J. Phys. Chem. C_. 125

(19), 10723–10737 (2021). Article  CAS  MATH  Google Scholar  * Soni, A. & Patey, G. N. Simulations of water structure and the possibility of ice nucleation on selected crystal planes of

K-feldspar. _J. Chem. Phys._ 150, 214504 (2019). Article  MATH  Google Scholar  * Mozzi, R. L. & Warren, B. E. The structure of vitreous silica. _J. Appl. Crystallogr._ 2 (4), 164–172

(1969). Article  ADS  CAS  MATH  Google Scholar  * Humphrey, W., Dalke, A. & Schulten, K. VMD: visual molecular dynamics. _J. Mol. Graph_. 14 (1), 33–38 (1996). Article  CAS  PubMed 

Google Scholar  * Van Der Spoel, D. et al. GROMACS: fast, flexible, and free. _J. Comput. Chem._ 26 (16), 1701–1718 (2005). Article  PubMed  MATH  Google Scholar  * Hoover, W. G. Canonical

dynamics: equilibrium phase-space distributions. _Phys. Rev. A_. 31 (3), 1695–1697 (1985). Article  ADS  CAS  MATH  Google Scholar  * Nosé, S. A unified formulation of the constant

temperature molecular dynamics methods. _J. Chem. Phys._ 81, 511–519 (1984). Article  ADS  MATH  Google Scholar  * Darden, T., York, D. & Pedersen, L. Particle mesh Ewald: an N⋅ log (N)

method for Ewald sums in large systems. _J. Chem. Phys._ 98 (12), 10089–10092 (1993). Article  ADS  CAS  MATH  Google Scholar  * Hess, B. et al. LINCS: a linear constraint solver for

molecular simulations. _J. Comput. Chem._ 18 (12), 1463–1472 (1997). Article  CAS  MATH  Google Scholar  * Conde, M. M., Rovere, M. & Gallo, P. High precision determination of the

melting points of water TIP4P/2005 and water TIP4P/Ice models by the direct coexistence technique. _J. Chem. Phys._ 147 (24), 244506 (2017). Article  ADS  CAS  PubMed  MATH  Google Scholar 

* Moore, E. B. et al. Freezing, melting and structure of ice in a hydrophilic nanopore. _Phys. Chem. Chem. Phys._ 12 (16), 4124 (2010). Article  CAS  PubMed  MATH  Google Scholar  * Nguyen,

A. H. & Molinero, V. Identification of clathrate hydrates, hexagonal ice, cubic ice, and liquid water in simulations: the CHILL+ algorithm. _J. Phys. Chem. B_. 119 (29), 9369–9376

(2015). Article  CAS  PubMed  MATH  Google Scholar  * Dash, J. G. Melting from one to two to three dimensions. _Contemp. Phys._ 43 (6), 427–436 (2002). Article  ADS  CAS  MATH  Google

Scholar  * Alejandra Sáncheza T K T I, M. et al. Experimental and theoretical evidence for bilayer-bybilayer surface melting of crystalline ice. Proc. Natl. Acad. Sci. 114(2):227–232.

(2017). * Pranami, G. & Lamm, M. H. Estimating error in diffusion coefficients derived from molecular dynamics simulations. _J. Chem. Theory Comput._ 11, 4586–4592 (2015). Article  CAS 

PubMed  MATH  Google Scholar  * Liu, P., Harder, E. & Berne, B. J. On the calculation of diffusion coefficients in confined fluids and interfaces with an application to the liquid-vapor

interface of water. _J. Phys. Chem. B_. 108, 6595–6602 (2004). Article  CAS  MATH  Google Scholar  * Mukherjee, S. & Bagchi, B. Entropic origin of the attenuated width of the ice–water

interface. _J. Phys. Chem. C_. 124 (13), 7334–7340 (2020). Article  CAS  MATH  Google Scholar  * Weiss, V. C. et al. Kinetic aspects of the thermostatted growth of ice from supercooled water

in simulations. _J. Chem. Phys._ 135 (3), 34701 (2011). Article  MATH  Google Scholar  * Baran, A., Rżysko, W. & MacDowell, L. G. Self-diffusion and shear viscosity for the TIP4P/Ice

water model. _J. Chem. Phys._ 158 (6), 64503 (2023). Article  CAS  MATH  Google Scholar  * Carignano, M. A., Shepson, P. B. & Szleifer, I. Molecular dynamics simulations of ice growth

from supercooled water. _Mol. Phys._ 103 (21–23), 2957–2967 (2005). Article  ADS  CAS  MATH  Google Scholar  * Uchida, S., Fujiwara, K. & Shibahara, M. Microscopic properties of forces

from ice solidification interface acting on silica surfaces based on molecular dynamics simulations. _Phys. Chem. Chem. Phys._ (2023). * Argyris, D., Cole, D. R. & Striolo, A. Dynamic

behavior of interfacial water at the silica surface. _J. Phys. Chem. C_. 113, 19591–19600 (2009). Article  CAS  MATH  Google Scholar  * Sun, C. Q. et al. The physics behind water

irregularity. _Phys. Rep._ 998, 1–68 (2023). Article  ADS  CAS  MATH  Google Scholar  Download references ACKNOWLEDGEMENTS The authors acknowledge funding support from National Natural

Science Foundation of China (Grant 41976162) and computational support from Westlake University HPC Center. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Environmental Science

and Engineering, Fudan University, Shanghai, China Shuting Ji * School of Engineering, Westlake University, Hangzhou, Zhejiang, China Shuting Ji, Sergio Andres Galindo Torres, Liang Lei 

& Ling Li * Key Laboratory of Coastal Environment and Resources of Zhejiang Province, Westlake University, Hangzhou, Zhejiang, China Sergio Andres Galindo Torres, Liang Lei & Ling Li

* School of Life Science, Westlake University, Hangzhou, Zhejiang, China Jinfeng Chen Authors * Shuting Ji View author publications You can also search for this author inPubMed Google

Scholar * Sergio Andres Galindo Torres View author publications You can also search for this author inPubMed Google Scholar * Jinfeng Chen View author publications You can also search for

this author inPubMed Google Scholar * Liang Lei View author publications You can also search for this author inPubMed Google Scholar * Ling Li View author publications You can also search

for this author inPubMed Google Scholar CONTRIBUTIONS S.J. conducted the MD simulation, data analysis and wrote the paper. J.C. supported the methodology and scripts. L.Li, L.Lei and S. G.

T. supported the data interpretation and reviewed the paper. L. Li also secured funding. CORRESPONDING AUTHORS Correspondence to Liang Lei or Ling Li. ETHICS DECLARATIONS COMPETING INTERESTS

The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional

affiliations. ELECTRONIC SUPPLEMENTARY MATERIAL Below is the link to the electronic supplementary material. SUPPLEMENTARY MATERIAL 1 RIGHTS AND PERMISSIONS OPEN ACCESS This article is

licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any

medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed

material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are

included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and

your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this

licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Ji, S., Torres, S.A.G., Chen, J. _et al._ Molecular dynamics

simulation of film water thickness and properties at different interfaces in partially saturated frozen soil systems. _Sci Rep_ 15, 2343 (2025). https://doi.org/10.1038/s41598-025-85975-3

Download citation * Received: 05 October 2024 * Accepted: 07 January 2025 * Published: 17 January 2025 * DOI: https://doi.org/10.1038/s41598-025-85975-3 SHARE THIS ARTICLE Anyone you share

the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer

Nature SharedIt content-sharing initiative KEYWORDS * Unsaturated frozen soil * Film water * Film water thickness, diffusivity * Mobility * Molecular dynamics