Non-uniform failure mechanism and stability control of mining roadway under deviatoric stress field

ABSTRACT Based on the elastic–plastic theory, the analytical formula of the second invariant _J_2 of deviatoric stress at any point around the circular roadway under the non-uniform stress

field is derived. The distribution law of _J_2 of surrounding rock under the three-dimensional non-isobaric stress field is studied by theoretical analysis and numerical simulation. Combined

with the butterfly failure theory of surrounding rock of roadway, the close relationship between the distribution pattern of _J_2 and the distribution pattern of plastic zone is found, and

the failure mechanism of surrounding rock is revealed. The results show that the distribution form of the second invariant _J_2 of deviatoric stress is closely related to the distribution

form of plastic zone. When the distribution of _J_2 of surrounding rock shows ‘round’, ‘oval’ and ‘butterfly’, the plastic zone shows the corresponding consistent form. When the second

invariant _J_2 of deviatoric stress produces stress concentration, the surrounding rock of roadway will produce large-scale damage. When the stress concentration is high, it may lead to

malignant expansion of surrounding rock of roadway. The distribution of the second invariant _J_2 of deviatoric stress is directional. When the principal stress rotates over a certain angle,

the second invariant _J_2 of deviatoric stress rotates over the same angle as the plastic zone. Under the influence of superimposed mining, the second invariant deviatoric stress _J_2 of

the wind tunnel of Yangchangwan 160,206 working face presents butterfly distribution, and the stress butterfly leaves present a certain degree of rotation. Based on the failure mode of

plastic zone, the corresponding optimization support scheme is proposed, and the engineering effect is good. SIMILAR CONTENT BEING VIEWED BY OTHERS ANALYTICAL SOLUTION OF SURROUNDING ROCK

STRESS AND PLASTIC ZONE OF RECTANGULAR ROADWAY UNDER NON-UNIFORM STRESS FIELD Article Open access 11 November 2024 ENERGY DRIVEN MECHANISM OF SURROUNDING ROCK DEFORMATION AND FAILURE OF

MINING ROADWAY AND CLASSIFIED CONTROL TECHNOLOGY Article Open access 30 April 2025 RESEARCH ON THE EVOLUTIONARY PATTERNS AND CONTROL OF SURROUNDING ROCK SUPERIMPOSED STRESS FIELD LOCAL AREA

LOADING IN DOUBLE-LAYER ISLAND FACE MAIN ROADWAY Article Open access 07 August 2024 INTRODUCTION Energy is a major event related to the overall situation of economic and social development,

and coal has long been the ballast and stabilizer of China’s energy security. With the increase of deep mining in coal mines and the increasing complexity of mining conditions, a series of

safety problems such as roadway instability are becoming more and more prominent. The stability control of deep roadway surrounding rock has become one of the research hotspots at home and

abroad1,2. In the problem of plastic mechanics, the development of plastic deformation of roadway surrounding rock is mainly controlled by deviatoric stress3, and deviatoric stress is of

great significance to the study of deformation and failure of roadway surrounding rock. In the problem of plastic mechanics, the development of plastic deformation of roadway surrounding

rock is mainly controlled by deviatoric stress4, and deviatoric stress is of great significance to the study of deformation and failure of roadway surrounding rock. Many scholars have

analyzed the stability of roadway surrounding rock based on deviatoric stress, and have achieved a series of research results5,6,7,8. Zhao et al.9 studied the distribution law of deviatoric

stress and strain energy density of roadway surrounding rock under three-dimensional non-isobaric stress field, deduced the mechanical solution of the maximum principal deviatoric stress

_S_1 and the minimum principal deviatoric stress _S_3 of circular roadway surrounding rock, and analyzed the distribution law of the maximum principal deviatoric stress and strain energy

density of roadway surrounding rock in different dominant stress fields. He et al.10 analyzed the stability of roadway surrounding rock with the maximum principal deviatoric stress as the

index, and obtained the distribution of deviatoric stress under different stress states. Based on this, a high-strength comprehensive control technology was proposed, and the industrial test

results were good. Wang et al.11 took the second invariant of deviatoric stress as the index, combined with the numerical simulation FLAC3D to analyze the stability control of surrounding

rock of coal roadway under the influence of multiple mining, and revealed the deformation and failure mechanism of coal rock under the influence of severe mining. In the aspect of deviatoric

stress distribution and plastic zone evolution law of roadway surrounding rock, Ma et al.12 studied the deviatoric stress field and plastic zone distribution law of roadway surrounding rock

based on the circular hole stress solution in elastic mechanics and the deviatoric stress theory in plastic mechanics, combined with Mohr–Coulomb criterion, and deduced the calculation

expression of deviatoric stress of roadway surrounding rock under non-uniform stress field and the analytical solution of plastic zone radius r. Yu et al.13 established the constitutive

equation of deviatoric stress and plastic zone distribution through the theory of rock mechanics, and proposed that the surrounding rock of roadway will form typical positive symmetric

instability mode and typical angular symmetric instability mode. Based on the plane strain problem, Shi et al.14 found that _J_2 will show a butterfly distribution, and clarified that the

second invariant of deviatoric stress has an important influence on the failure distribution of plastic zone. In this paper, the mining roadway of Yangchangwan Mine is taken as the

engineering background, and the deviatoric stress environment and failure characteristics of the surrounding rock of the mining roadway are taken as the starting point. By introducing the

second invariant _J_2 of the deviatoric stress tensor which can characterize the shear stress failure strength, the relationship between the distribution form and direction of the _J_2

stress field and the plastic zone of the surrounding rock of the roadway under the deviatoric stress field is established, and the mechanical mechanism of the formation of different forms of

the plastic zone of the surrounding rock of the roadway in the deviatoric stress field is revealed. On this basis, the temporal and spatial evolution law of the stress and plastic zone of

the mining roadway in Yangchangwan Mine during the whole process of excavation and mining is studied, and the non-uniform failure mechanism of the surrounding rock of the mining roadway

under the deviatoric stress field is revealed. The stability control principle of surrounding rock of mining roadway under deviatoric stress field is put forward, and the control technology

of surrounding rock of mining roadway under deviatoric stress field is formed, and the field industrial test is carried out, so as to enrich the theory of plastic zone of surrounding rock of

roadway and the practice of stability control. ANALYTICAL SOLUTION OF THE SECOND INVARIANT _J_ 2 OF DEVIATORIC STRESS ELASTIC–PLASTIC ANALYSIS OF SURROUNDING ROCK UNDER NON-UNIFORM STRESS

FIELD In underground engineering, the surrounding rock of roadway is in the three-dimensional stress field. Due to the complexity of its mathematical and mechanical analysis, the previous

scholars usually use the plane strain problem to discuss. However, the model ignores the axial force of the roadway and cannot truly describe the three-dimensional stress environment of the

roadway. Some theoretical studies have shown that the axial force of the roadway has an effect on the range of the plastic zone of the surrounding rock of the roadway, and the influence of

the axial stress is different with the change of the stress state. Therefore, the three-dimensional stress environment of the roadway should be fully considered. When dealing with roadways

with complex stress conditions such as inclined roadways and cross-layer roadways, it should be regarded as a three-dimensional space problem in elastic mechanics1,15. The analysis diagram

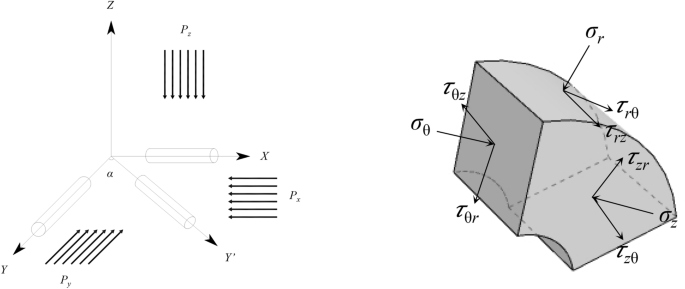
of roadway surrounding rock affected by three-dimensional stress is shown in Fig. 1. In the Figure _P__x_, _P__y_ and _P__z_ represent the three-dimensional stress of _X_, _Y_ and _Z_ axes.

Under the condition of three-dimensional stress, according to the theory of elastic mechanics15, the stress solution of any point around the surrounding rock of circular roadway in polar

coordinate system can be obtained as follows: $$\begin{aligned} \sigma_{r} &= \frac{{p_{x} + p_{z} }}{2}\left( {1 - \frac{{a^{2} }}{{r^{2} }}} \right) + \frac{{p_{x} - p_{z} }}{2}\left(

{1 - 4\frac{{a^{2} }}{{r^{2} }} + 3\frac{{a^{4} }}{{r^{4} }}} \right)\cos 2\theta , \hfill \\ \sigma_{\theta } &= \frac{{p_{x} + p_{z} }}{2}\left( {1 + \frac{{a^{2} }}{{r^{2} }}} \right)

- \frac{{p_{x} - p_{z} }}{2}\left( {1 + 3\frac{{a^{4} }}{{r^{4} }}} \right)\cos 2\theta , \hfill \\ \sigma_{y} &= p_{y} - 2\mu (p_{x} - p_{z} )\frac{{a^{2} }}{{r^{2} }}\cos 2\theta ,

\hfill \\ \tau_{r\theta } &= \frac{{p_{x} - p_{z} }}{2}\left( {1 + 2\frac{{a^{2} }}{{r^{2} }} - 3\frac{{a^{4} }}{{r^{4} }}} \right)\sin 2\theta , \hfill \\ \end{aligned}$$ (1) where _σ_r

is the radial stress at any point, _σ_θ is the circumferential stress at any point, _σ_y is the axial stress of the roadway, _τ_rθ is the shear stress at any point, _a_ is the radius of the

surrounding rock of the roadway, _r_ and _θ_ are the polar coordinates of any point around the roadway, _ν_ is the Poisson’s ratio of the surrounding rock of the roadway. The principal

stress expression of any point of roadway surrounding rock can be obtained by elastic mechanics: $$\begin{gathered} \sigma_{1} = \frac{{\sigma_{r} + \sigma_{\theta } }}{2} + \frac{1}{2}\sqrt

{\left( {\sigma_{r} - \sigma_{\theta } } \right)^{2} + 4\tau_{r\theta }^{2} } , \hfill \\ \sigma_{2} = \sigma_{y} , \hfill \\ \sigma_{3} = \frac{{\sigma_{r} + \sigma_{\theta } }}{2} -

\frac{1}{2}\sqrt {\left( {\sigma_{r} - \sigma_{\theta } } \right)^{2} + 4\tau_{r\theta }^{2} } , \hfill \\ \end{gathered}$$ (2) where _σ_1 is the maximum principal stress at any point, _σ_2

is the intermediate principal stress at any point, and _σ_3 is the minimum principal stress at any point. ANALYTICAL SOLUTION OF THE SECOND INVARIANT J2 OF DEVIATORIC STRESS OF SURROUNDING

ROCK Under general conditions, the volume and shape of the surrounding rock of the roadway will change under the action of external force. In the classical plastic theory and elastic theory,

the stress sphere tensor only produces volumetric strain and has no shape change. The deviatoric stress tensor will produce shear deformation, which reflects the degree to which the actual

stress state of an object deviates from the uniform stress state. Therefore, the plastic deformation of rock mass is closely related to the deviatoric stress tensor3,16. Here, the spherical

tensor component of the stress tensor is denoted as: $$\sigma_{m} { = }\frac{1}{3}\left( {\sigma_{{1}} + \sigma_{{2}} + \sigma_{{3}} } \right),$$ (3) $$\sigma { = }\left(

{\begin{array}{*{20}c} {\sigma_{1} } & 0 & 0 \\ {} & {\sigma_{1} } & 0 \\ {S{\text{ym}}} & {} & {\sigma_{1} } \\ \end{array} } \right){ = }\left(

{\begin{array}{*{20}c} {\sigma_{{\text{m}}} } & 0 & 0 \\ {} & {\sigma_{{\text{m}}} } & 0 \\ {S{\text{ym}}} & {} & {\sigma_{{\text{m}}} } \\ \end{array} } \right) +

\left( {\begin{array}{*{20}c} {\sigma_{{1}} - \sigma_{{\text{m}}} } & 0 & 0 \\ {} & {\sigma_{{2}} - \sigma_{{\text{m}}} } & 0 \\ {S{\text{ym}}} & {} & {\sigma_{{3}} -

\sigma_{{\text{m}}} } \\ \end{array} } \right).$$ (4) The left side of Eq. (4) is the stress tensor _σ_, the first term on the right side is the stress sphere tensor, and the second term is

the stress partial tensor. According to the theory of elastoplastic mechanics, the size of the deviatoric stress tensor will change with the change of the coordinate system. The randomness

of the coordinate system leads to the randomness of the tensor component, and the deviatoric stress tensor invariant will not change due to the change of the coordinate system17. The second

invariant _J_2 of deviatoric stress has rich physical meaning, and its expression is as follows: $$\begin{aligned} J_{2} = & \frac{1}{6}\left[ {\left( {\sigma_{1} - \sigma_{2} }

\right)^{2} + \left( {\sigma_{2} - \sigma_{3} } \right)^{2} + \left( {\sigma_{3} - \sigma_{1} } \right)^{2} } \right] \, \\ = & \, \frac{1}{3}\left[ {\sigma_{1}^{2} + \sigma_{2}^{2} +

\sigma_{3}^{2} - \sigma_{1} \sigma_{2} - \sigma_{2} \sigma_{3} - \sigma_{3} \sigma_{1} } \right] \, {.} \\ \end{aligned}$$ (5) It can be seen from Eq. (5) that _J_2 is the comprehensive

quantitative index of _σ_1, _σ_2, _σ_3, and the relationship between _J_2 and each shear stress is shown in Eq. (6): $$J_{2} = \frac{1}{3}q^{2} = \frac{3}{2}\tau_{8}^{2} =

\frac{1}{2}\tau_{\sigma }^{2} = \tau_{s}^{2} .$$ (6) The above formula shows that _J_2 has a fixed relationship with the generalized shear stress _q_, octahedral shear stress \(\tau^{8}\)

and pure shear stress \(\tau_{\sigma }\). In the plastic theory, the main reason for the yield failure of the material is caused by the shear stress of the material. Therefore, the second

invariant _J_2 of deviatoric stress can reflect the failure of rock mass and can better reflect the essence of rock mass deformation and failure. At this time, the Eq. (1) is brought into

the Eq. (2) the principal stress transformation formula _σ_1, _σ_2, _σ_3 is brought into the Eq. (5), and the analytical expression of the second invariant _J_2 of the deviatoric stress at

any point around the roadway can be obtained as the Eq. (7): $$\begin{aligned} J_{2} = & \frac{{{9}B^{2} }}{4}\left( \frac{a}{r} \right)^{8} - \left[ {{3}B^{{2}} { + }\frac{3}{2}AB\cos

2\theta } \right]\left( \frac{a}{r} \right)^{6} + \left[ {\left( {\frac{5}{2}{ + }\frac{1}{3}(2\mu - 1)^{2} } \right)B^{2} \cos^{2} 2\theta { + }\frac{1}{{4}}A^{2} { + }AB\cos 2\theta -

\frac{1}{2}B^{2} \sin^{2} 2\theta } \right]\left( \frac{a}{r} \right)^{4} \\ & + \left[ {B^{2} (\sin^{2} 2\theta - \cos^{2} 2\theta ) + AB(\frac{2}{3}\mu - \frac{5}{6})\cos 2\theta -

\frac{2}{3}p_{y} B(2\mu - 1)\cos 2\theta } \right]\left( \frac{a}{r} \right)^{2} + \left[ {\frac{{B^{2} }}{4} + \frac{{A^{2} }}{12} - \frac{1}{3}(A - p_{y} )} \right] \\ \end{aligned}$$ (7)

Among them, \(A = p_{x} + p_{z} ,B = p_{x} - p_{z}\), here let: $$\begin{gathered} K_{1} = \frac{{9}}{4}(p_{x} - p_{z} )^{2} , \hfill \\ K_{2} = - 3(p_{x} - p_{z} )^{2} -

\frac{3}{2}(p_{x}^{2} - p_{z}^{2} )\cos 2\theta , \hfill \\ K_{3} = (p_{x} - p_{z} )^{2} \cos^{2} 2\theta \left[ {\frac{5}{2} + \frac{1}{3}(2\mu - 1)^{2} } \right] + \frac{1}{4}(p_{x} +

p_{z} )^{2} + (p_{x}^{2} - p_{z}^{2} )\cos 2\theta - \frac{1}{2}(p_{x} - p_{z} )^{{2}} \sin^{{2}} 2\theta , \hfill \\ K_{4} = (p_{x} - p_{z} )^{2} (\sin^{2} 2\theta - \cos^{2} 2\theta ) +

(p_{x}^{2} - p_{z}^{2} )\cos 2\theta \left[ {\frac{2}{3}\mu - \frac{{5}}{{6}}} \right] - \frac{2}{3}p_{y} (p_{x} - p_{z} )(2\mu - 1)\cos 2\theta , \hfill \\ K_{5} = \frac{1}{4}(p_{x} - p_{z}

)^{2} + \frac{1}{12}(p_{z} + p_{x} )^{2} - \frac{1}{3}(p_{z} + p_{x} )p_{y} + \frac{1}{3}p_{y}^{2} . \hfill \\ \end{gathered}$$ Here, according to the simplification, the second invariant

_J_2 of the deviatoric stress at any point of the roadway surrounding rock can be resolved into an eight-order implicit equation related to the radius, such as Eq. (8): $$J_{2} = K_{1}

\left( \frac{a}{r} \right)^{8} + K_{2} \left( \frac{a}{r} \right)^{6} + K_{3} \left( \frac{a}{r} \right)^{4} + K_{4} \left( \frac{a}{r} \right)^{2} + K_{5} .$$ (8) Under the condition that

_P__x_, _P__y_, _P__z_ and Poisson’s ratio v are given, the second invariant _J_2 of deviatoric stress at any point of roadway surrounding rock can be calculated by taking _r_ and _θ_ into

account. STUDY ON THE RELATIONSHIP BETWEEN _J_ 2 AND PLASTIC ZONE MORPHOLOGY STUDY ON J2 DISTRIBUTION LAW OF ROADWAY SURROUNDING ROCK In order to further explore the relationship between the

second invariant _J_2 of deviatoric stress and the plastic zone shape of roadway surrounding rock, the _P__x_, _P__y_ and _P__z_ of different ratios are brought into Eq. (8), and the second

invariant distribution map of deviatoric stress under different stress field conditions is drawn by using the built-in command of Maple software. At present, the existing research proposes

that the plastic zone of roadway surrounding rock has three forms: circular, elliptical and butterfly. The circular form only exists when _P__x_:_P__y_ = 1. With the increase of

_P__x_:_P__y_ ratio, the plastic zone of surrounding rock changes from circular to elliptical and then to butterfly. Here we fix the size of _P__z_ is 15 MPa, _P__x_:_P__y_ = 1, Poisson’s

ratio _v_ = 0.25, the radius of the roadway is 3 m. Three groups of loading schemes are set according to different lateral pressure coefficients, and the stress loading scheme is shown in

Table 1. The distribution of the second invariant _J_2 isoline of the deviatoric stress of roadway surrounding rock under different stress loading conditions is shown in Fig. 2. From the

isoline stress diagram, it can be seen that. The distribution of the second invariant_ J_2 isoline of the deviatoric stress of roadway surrounding rock under different stress loading

conditions is shown in Fig. 2. When _μ_ = 1.0, the size of _J_2 around the roadway surrounding rock is exactly the same, and the size of _J_2 around the roadway is decreasing in a ‘ring’

shape. When _μ_ = 0.8, the distribution around the roadway _J_2 began to show non-uniform characteristics, the _J_2 at the roof of the roadway gradually decreased, the deviatoric stress of

the two sides of the roadway gradually increased, and the deviatoric stress contour showed a transverse elliptical distribution. When _μ_ = 0.4, the deviatoric stress at the roof of the

roadway continues to decrease, and the deviatoric stress at the side of the roadway gradually increases. As the distance from the roadway increases, the deviatoric stress of the roadway

gradually expands to the angular bisector of the four quadrants, and the shape of the deviatoric stress of the surrounding rock of the roadway presents a butterfly shape. From the above

comprehensive analysis, it can be seen that the _J_2 distribution patterns of roadway surrounding rock under different stress environments are roughly divided into three types: ‘round’,

‘oval’ and ‘butterfly’. Under different stress conditions, the concentration degree of _J_2 at different positions around the roadway is quite different. When the surrounding rock of the

roadway is in the state of hydrostatic pressure, the stress concentration degree of the roadway is completely consistent. When the partial stress form of the roadway is elliptical, the

support of the two sides or the roof and floor should be paid attention to. When the partial stress of the roadway is butterfly shape, the stress concentration of the four quadrant angle

bisector of the roadway should be paid attention to. THEORETICAL STUDY ON THE RELATIONSHIP BETWEEN J2 DISTRIBUTION AND PLASTIC ZONE MORPHOLOGY After roadway excavation, energy release occurs

around the roadway, and deviatoric stress concentration occurs around the roadway. Deviatoric stress _J_2 leads to plastic deformation of rock mass, which may lead to malignant expansion of

plastic zone in severe cases. Therefore, it is of great significance for reasonable roadway support design to deeply study the relationship between _J_2 distribution law and plastic zone

morphology of roadway. In Refs.18,19, the eighth-order implicit equation of plastic zone boundary at any point of surrounding rock of circular roadway in non-uniform stress field is derived.

The approximate implicit solution is based on the most commonly used Mohr–Coulomb criterion as the failure criterion, and the stress solution of any point of surrounding rock of circular

roadway in elastic mechanics theory is brought into the criterion. According to the eight-order implicit equation of the plastic zone, some specific parameter values are set, _a_ = 3 m, _φ_ 

= 27°, _C_ = 2 MPa. By bringing the above three stress loading schemes into the equation, the plastic zone morphology under different stress loading conditions is obtained as shown in Fig. 

3. Reference20 gives the criteria for judging the shape of the plastic zone of the surrounding rock of the roadway. Through the shape distribution of the plastic zone in Fig. 3 and the

criteria for judging the shape, the following rules can be obtained: * (1) When the lateral pressure coefficient is 0.4, the longitudinal axis and transverse axis of the coordinate shrink in

the direction of the center of the coordinate circle, and the boundary of the plastic zone in the coordinate quadrant expands. The maximum boundary of the plastic zone of the roadway occurs

in four quadrants, and the shape of the plastic zone is ‘vertical butterfly’. * (2) When the lateral pressure coefficient is 0.8, the minimum boundary is located on the longitudinal axis of

the coordinate axis, the elliptical focus is located on the transverse axis, and the shape of the plastic zone is ‘transverse ellipse’. * (3) When the lateral pressure coefficient is 1.0,

in the hydrostatic pressure field, the plastic zone boundary of the roadway surrounding rock is a standard ‘circular’ shape. Through the study of _J_2 distribution law under different stress

fields of roadway surrounding rock in “Study on J2 distribution law of roadway surrounding rock” section and the study of plastic zone morphology under different stress fields in

“Theoretical study on the relationship between J2 distribution and plastic zone morphology” section, it can be seen that under different stress fields, the distribution pattern of _J_2 is

almost the same as that of plastic zone, showing three forms of ‘circle’, ‘oval’ and ‘butterfly’. In summary, it can be found that the distribution pattern of _J_2 is closely related to the

shape of plastic zone. NUMERICAL SIMULATION STUDY ON THE RELATIONSHIP BETWEEN J2 DISTRIBUTION AND PLASTIC ZONE MORPHOLOGY FLAC3D can simulate the stress characteristics and plastic flow

analysis of three-dimensional structures such as soil and rock. Therefore, in this paper, the finite difference method is used to simulate the distribution characteristics of the second

invariant _J_2 of deviatoric stress and the failure range and morphology of plastic zone under different three-dimensional stress fields, so as to analyze the close relationship between

deviatoric stress morphology and plastic zone morphology. In this paper, a numerical model with a circular roadway section is established. This model has a total of 153,360 units. The

surrounding rock is regarded as the equivalent rock mass material of the same sex. The rock mechanics parameters are shown in Table 2. The Mohr–Coulomb model is used. The surrounding and

bottom of the model are set as the displacement boundary, the roof is set as the stress boundary, and the upper load is 15 MPa. In this simulation, three simulation schemes under different

stress environments are set up, and different load loading parameters are shown in Table 2 in “Study on J2 distribution law of roadway surrounding rock” section. Figure 4 shows the _J_2

distribution diagram under different lateral pressure coefficients. It can be seen from the Fig. that: (1) Due to the excavation of the roadway, the second invariant deviatoric stress is

redistributed, the deviatoric stress unloading occurs around the excavation space, and the _J_2 concentration area develops to the deep part of the roadway. (2) When the lateral pressure

coefficient is 0.4, the distribution of _J_2 presents a butterfly shape, and the deviatoric stress _J_2 is mainly concentrated in the side and four corners of the roadway, and the deviatoric

stress at the side and wing angle increases first and then decreases with the increase of surrounding rock depth. (3) When the lateral pressure coefficient is 0.8, the distribution of _J_2

presents an elliptical shape, and the concentration of _J_2 in the two sides is greater than that in the roof and floor. (4) When the lateral pressure coefficient is 1, the distribution of

_J_2 presents a circular shape, and the concentration of _J_2 around the roadway is very uniform. The distribution diagram of plastic zone under different lateral pressure coefficients is

shown in Fig. 5. When the lateral pressure coefficient is 0.4, the plastic zone of surrounding rock is characterized by butterfly shape. When the lateral pressure coefficient is 0.8, the

plastic zone of surrounding rock is characterized by elliptical shape. When the lateral pressure coefficient is 1.0, the plastic zone of surrounding rock is characterized by circular shape.

Through the numerical simulation results of Figs. 4 and 5, it can be seen that the distribution of the second invariant deviator stress _J_2 of the surrounding rock of the roadway is closely

related to the distribution of the plastic failure of the surrounding rock. When the distribution of _J_2 presents butterfly, oval and circular, the plastic zone failure also presents the

corresponding form. STUDY ON _J_ 2 DIRECTIONALITY OF SURROUNDING ROCK UNDER NON-UNIFORM STRESS FIELD In the process of advancing the working face, the direct roof is constantly falling due

to the increase of the exposed area, and the hinged structure formed by the rock block during the rotation process leads to the rotation of the local stress field direction of the

surrounding rock of the roadway. When the stress field of the roadway rotates, it will lead to the rotation of the plastic zone of the surrounding rock of the roadway. When the shape of the

plastic zone is’butterfly’, the rotation of the stress field will cause the butterfly leaf to be located near the roof, which may lead to serious roof fall disaster. THEORETICAL ANALYSIS OF

J2 DIRECTIONALITY OF SURROUNDING ROCK UNDER NON-UNIFORM STRESS FIELD In order to study the directionality of the second invariant deviator stress _J_2, the deflection angle α is brought into

Eq. (7) to obtain the expression of the second invariant deviator stress when the stress rotates (Eq. 9): $$\begin{aligned} J_{2} = & \frac{{{9}B^{2} }}{4}\left( \frac{a}{r} \right)^{8}

- \left[ {{3}B^{{2}} { + }\frac{3}{2}AB\cos 2(\theta - \alpha )} \right]\left( \frac{a}{r} \right)^{6} + \left[ \begin{gathered} \left( {\frac{5}{2}{ + }\frac{1}{3}(2\mu - 1)^{2} }

\right)B^{2} \cos^{2} 2(\theta - \alpha ){ + } \hfill \\ \frac{1}{{4}}A^{2} { + }AB\cos 2(\theta - \alpha ) - \frac{1}{2}B^{2} \sin^{2} 2(\theta - \alpha ) \hfill \\ \end{gathered}

\right]\left( \frac{a}{r} \right)^{4} \\ & + \left[ \begin{gathered} B^{2} (\sin^{2} 2(\theta - \alpha ) - \cos^{2} 2(\theta - \alpha )) + \hfill \\ AB(\frac{2}{3}\mu - \frac{5}{6})\cos

2(\theta - \alpha ) - \frac{2}{3}p_{y} B(2\mu - 1)\cos 2(\theta - \alpha ) \hfill \\ \end{gathered} \right]\left( \frac{a}{r} \right)^{2} + \left[ {\frac{{B^{2} }}{4} + \frac{{A^{2} }}{12} -

\frac{1}{3}(A - p_{y} )} \right]. \\ \end{aligned}$$ (9) In order to study the influence of principal stress deflection on _J_2 distribution, the deflection angles α of 0°, 15°, 30°, 45°,

60°, 75° and 90° are brought into Eq. (9). The _J_2 distribution diagram when _P__x_ = 20 MPa, _P__y_ = 10 MPa, _P__z_ = 8 MPa, _v_ = 0.25, _a_ = 3 m and 5 m away from the center of the

roadway is shown in Fig. 6: It can be clearly seen from Fig. 6 that under the above stress environment, the _J_2 distribution at the radius of 5 m of the roadway presents a butterfly shape,

and the _J_2 distribution will deflect to a certain extent with the rotation of the principal stress. When the principal stress of the roadway deflects at a certain angle, the roadway _J_2

also deflects through the same angle, and the deflection of the principal stress leads to a significant difference in the distribution of _J_2 values around the roadway. And when α is 0°,

the _J_2 distribution value of the roadway roof and the wing angle is much larger than that of the two sides. When α is 45°, the deviatoric stress value of the first three quadrants of the

roadway coordinate system is larger. When α is 90°, the _J_2 distribution value of the two sides of the roadway and the wing angle is much larger than that of the roof and floor. In the

literature21, the boundary equation of plastic zone under the condition of principal stress deflection under non-hydrostatic pressure is derived. The above stress environment is brought into

the equation to obtain the plastic zone distribution diagram of roadway surrounding rock under different deflection angles as shown in Fig. 7 (_a_ = 3 m, _φ_ = 29°, _C_ = 3 MPa). From Fig. 

7, it can be seen that under the above stress environment, the shape of the plastic zone of the surrounding rock of the roadway presents a butterfly distribution, which is consistent with

the distribution of the above deviatoric stress _J_2. The butterfly leaf in the plastic zone will deflect with the rotation of the principal stress. When the principal stress rotates at a

certain angle, the plastic zone will also deflect at the same angle, and the shape of the plastic zone will not change. In addition, there is a one-to-one correspondence between the _J_2

value and the depth of the plastic zone. The larger the _J_2 value of the surrounding rock of the roadway, the greater the depth of the plastic zone. When α is 0°, the failure of surrounding

rock mainly occurs in the roof and floor of the roadway and the four corners, and almost no damage occurs in the two sides. When α is 45°, the roof and floor, two sides and one and three

quadrants of the roadway are damaged in a large range, while the damage range near the angle bisector of the two and four quadrants is smaller. When α is 90°, a large range of damage occurs

at the two sides of the roadway and the wing angle, and the roof and floor are almost not damaged. NUMERICAL SIMULATION STUDY ON J2 DIRECTIONALITY OF SURROUNDING ROCK UNDER NON-UNIFORM

STRESS FIELD On the basis of theoretical analysis, the numerical simulation analysis of the above six different stress deflection angles is carried out. The plastic zone and _J_2

distribution obtained by numerical simulation analysis are shown in Fig. 8 (_a_ = 3 m, _φ_ = 29°, _C_ = 3 MPa). It can be seen from Fig. 8 that _J_2 presents a butterfly distribution under

different stress deflection angles, and the stress butterfly leaf deflects with the rotation of the principal stress direction. The rotation angle is almost the same as the stress deflection

angle, which is consistent with the above theoretical analysis results. For the distribution of plastic zone of surrounding rock, the shape of plastic zone under different stress deflection

angles is butterfly, which is completely consistent with the distribution of _J_2, and the deflection angle of butterfly leaf in plastic zone is almost consistent with the deflection angle

of principal stress, which is also consistent with the above theoretical analysis. Combined with the schematic diagram of plastic zone and deviatoric stress distribution, it can be seen that

when the _J_2 distribution is deflected, it may lead to _J_2 concentration near the roadway roof. When the concentration of deviatoric stress is high, it will lead to a wide range of uneven

plastic expansion of the roof. In severe cases, it may lead to roof leakage and roof fall accidents. Based on the above analysis, it can be seen that when the principal stress rotates at a

certain angle, the second invariant _J_2 of the deviatoric stress of the surrounding rock and the plastic zone both deflect through the same angle. Combined with the analysis of “Theoretical

study on the relationship between J2 distribution and plastic zone morphology” section, it can be seen that when the stress concentration occurs in _J_2, it will lead to a large range of

damage to the surrounding rock. Therefore, when analyzing the stability of roadway surrounding rock, we should pay attention to the directionality of the second invariant _J_2 of roadway

deviatoric stress, and focus on supporting the _J_2 concentration area. PROJECT APPLICATIONS ENGINEERING OVERVIEW AND DEFORMATION AND FAILURE OF SURROUNDING ROCK The average vertical depth

of 160,206 fully mechanized caving face in Yangchangwan Coal Mine is 592 m from the ground. The north is bounded by the 1#open-off cut of 160,206 working face, and the south is bounded by

the return air downhill in the north wing of 16 mining area. The working face is adjacent to the goaf of 120,212 working face, and the coal pillar is set at 30 m. The 160,206 working face

adopts the longwall retreating top coal caving mining method. The mining height is 4 m, the top coal thickness is 5.3 m, and the mining ratio is _N_ = 1:1.33. The return air roadway of

160,206 working face is 2387 m, and the working face distribution diagram is shown in Fig. 9. The second-layer coal roof is a composite roof, and the lithology changes greatly. There is a

thin layer of false roof in the local area, and the thickness changes greatly. The bottom of the direct roof often contains several layers of thin coal, which causes the roof to fall easily.

There are some deformation and failure characteristics of surrounding rock in some areas of 160,206 return air roadway, such as asymmetric large deformation of roof, serious roof fall,

distorted deformation and fracture failure of roof steel beam, cracking and falling of floor heave and shotcrete layer, and over-width of roadway rib, as shown in Fig. 10. STUDY ON THE

DISTRIBUTION OF THE SECOND INVARIANT J2 IN RETURN AIRWAY In this paper, FLAC3D numerical model is established based on the engineering background of 120,212 and 160,206 working face in

Yangchangwan. The dimensions of the model in _X_, _Y_ and _Z_ directions are 850 m, 1170 m and 150 m, respectively. The whole model is composed of 1,634,270 grids, of which 160,206 return

air roadway is meshed, and the double yield model is used to fill the goaf. When the working face of the upper section is advanced, the _J_2 distribution cloud map of 160,206 return air

roadway is shown in Fig. 11. When the left side of the return air roadway is 120,212 solid coal area, the mining roadway is less affected by the abutment pressure of the lateral goaf, and

the _J_2 stress concentration degree of the surrounding rock of the roadway is low and basically presents a uniform and symmetrical ‘oval’ distribution; when the left side of the return

airway is 120,212 solid coal-goaf transition area, the _J_2 stress concentration of the surrounding rock of the roadway gradually increases due to the combined influence of the lateral goaf

abutment pressure and the original rock stress. When the return airway is 370 m away from the open-off cut, the _J_2 stress form gradually changes from ‘oval’ to ‘butterfly’. Due to the

stress deflection, the _J_2 butterfly leaf gradually deflects to the side of the goaf, and the _J_2 stress changes from the uniform and symmetrical distribution of the solid coal stage to

the non-uniform and asymmetric distribution. The stress is mainly concentrated in the coal pillar side and the floor near the coal pillar side, as well as the coal wall side and the roof

near the coal wall side. When the left side of the return air roadway is 120,212 goaf area, the joint influence of lateral abutment pressure and original rock stress is intensified. At this

time, the concentration degree of _J_2 stress butterfly leaf is increasing, and the _J_2 stress form is gradually changed from ‘butterfly’ to ‘butterfly’, and the deflection angle of stress

butterfly leaf remains basically unchanged. At the same time, the _J_2 stress butterfly leaf on the side of the coal wall is stably expanded, and the stress concentration degree is gradually

transferred from the shallow part to the deep part. The _J_2 stress butterfly leaf on the side of the coal pillar and the _J_2 stress in the lateral goaf are connected in a large range, and

the instability of the butterfly leaf stress is generated. Rapid expansion is not conducive to the stability of the surrounding rock of the roadway. With the increase of the distance from

the open-off cut, although the’butterfly shape’ has different expansion ranges, it basically remains unchanged in shape. The _J_2 distribution cloud diagram of 160,206 return airway under

different working face advancement is shown in Fig. 12. In the process of 160,206 working face gradually advancing towards 120,212 goaf area, the surrounding rock _J_2 of roadway is always

under the influence of high deviatoric stress environment. At the 10 m position of the advanced working face, _J_2 has different degrees of stress concentration in the coal pillar side and

the coal wall side. With the increase of the distance of the advanced working face, _J_2 is mainly affected by the complex superposition of the abutment pressure of the lateral goaf and the

mining stress in front of the working face. Its morphological evolution law is basically the same as that of the excavation influence stage. At this stage, the roadway coal pillar side and

its floor, coal wall side and its surrounding rock within the roof range have obvious _J_2 stress concentration. This is inevitably related to the monitoring results of the surrounding rock

of the roadway, that is, the roof of the coal pillar, the floor of the coal wall and the non-uniform deformation and failure of the two sides. Based on the close relationship between the

distribution pattern of the second invariant _J_2 of the deviatoric stress tensor and the distribution pattern of the plastic zone obtained from the above analysis, that is, when the

distribution of _J_2 in the surrounding rock of the roadway presents ‘circular’, ‘elliptical’ and ‘butterfly’, the plastic zone of the surrounding rock of the roadway also presents a

corresponding consistent shape. Based on the analysis of the dynamic distribution law of _J_2 and the evolution law of the plastic zone in the surrounding rock of the roadway under the

deviatoric stress field, the _J_2 and the plastic zone morphology at different positions of the return air roadway from the open-off cut before and after the advance of the 160,206 working

face are selected, as shown in Figs. 13 and 14. The law between _J_2 and plastic zone of roadway surrounding rock in shape and direction during excavation and mining is compared and

analyzed, and the non-uniform failure mechanism of roadway surrounding rock during excavation is revealed. From the diagram, it can be seen that the 160,206 return air roadway is affected by

the 120,212 lateral goaf at different positions in the mining influence stage such as excavation and mining. There are three forms of ‘oval’, ‘butterfly’ front state and ‘butterfly’ in the

surrounding rock _J_2 of the roadway. Among them, the ‘butterfly’ front state and ‘butterfly’ form are non-uniformly and asymmetrically distributed, and the corresponding surrounding rock

plastic zone also has three forms of ‘oval’, ‘butterfly’ front state and ‘butterfly’. And the plastic zone of surrounding rock deflects in the same direction and angle with the deflection of

_J_2 stress. Therefore, there is a one-to-one correspondence between _J_2 stress and plastic zone in the form and direction of mining roadway surrounding rock under deviatoric stress field,

and the depth of stress concentration and plastic zone development is basically consistent. SURROUNDING ROCK CONTROL TECHNOLOGY PROGRAM Based on the above analysis, the surrounding rock

control idea of’whole-part-region’ three-dimensional integration of mining roadway under partial stress field is put forward22,23: * (1) Regulating the high deviatoric stress environment of

the roadway to prevent the formation of _J_2 stress concentration in the roadway. The main measures include: The parameters of deep hole pre-splitting blasting are shown in Fig. 15. Firstly,

a deep hole pre-splitting blasting pressure relief drilling field is arranged every 20 m on the side roof of the coal wall. Three holes are constructed in each drilling field. The diameter

of the hole is 79 mm, the depth of the hole is 30 m, and the hole is about 1 m from the side of the roadway. The three holes are perpendicular to the direction of the roadway, and the

drilling is carried out along the elevation angle of 55°, 65° and 75° respectively. The charge of each hole is 25 kg, 28 kg and 30 kg respectively, and the length of the hole is not less

than 10 m. On the side roof of the coal pillar, a deep hole pre-splitting blasting pressure relief drilling field is arranged every 10 m, and one hole is constructed in each drilling field.

The hole diameter is 79 mm and the hole depth is 30 m. The hole mouth is about 1m away from the roadway side, the borehole is perpendicular to the direction of the roadway, the elevation

angle is 75°, the charge of each borehole is 25 kg, and the sealing length is not less than 10 m. * (2) According to the development degree and range of the plastic zone of the surrounding

rock of the roadway, the sensitive position of the roadway section is strengthened and the anchoring end of the supporting body is in the elastic zone of the rock mass. The asymmetric long

and short bolt (cable) coordinated strengthening support can not only improve the stress state of the shallow surrounding rock, inhibit the malignant expansion of the butterfly wing in the

plastic zone, but also make the roadway maintain unified coordinated deformation and stability. On the basis of the advanced deep hole pre-splitting blasting of the surrounding rock of the

roof as a whole, the surrounding rock of the local roadway is still seriously deformed, showing serious drums on both sides. The bottom heave of the coal pillar side is greater than that of

the coal wall side, and the subsidence of the coal wall side roof is greater than the non-uniform deformation and failure characteristics of the coal pillar side. In view of the’butterfly’

non-uniform distribution of the plastic zone of the surrounding rock under the mining-induced deviatoric stress field, the existing roof support is a non-uniform support method with the

center of the roadway as the symmetrical axis and the side support of the coal pillar greater than the side support of the coal wall. While bearing serious costs, it does not provide good

support for the surrounding rock of the roadway, and the deformation of the surrounding rock of the roadway is large. Based on the existing roadway support, it is proposed to strengthen the

coordinated support of asymmetric long and short anchor cables in the local area of the surrounding rock section of the roadway. The main support parameters are shown in Table 3 and Fig. 16.

In order to verify the rationality of the support scheme and the pressure relief of the borehole, the surface displacement of the roadway was monitored in the return air roadway of 160,206

working face. The field engineering test results show that the J2 stress field shape is regulated by the deep hole pre-splitting blasting of the roof, the malignant expansion of the

butterfly wing in the plastic zone is inhibited by the asymmetric long and short anchor cable, the hidden danger of roof fall in the key area is eliminated by the pumping pillar and the

non-repeated support unit support, the deformation of the roadway roof is effectively reduced, and the safe and efficient production of the working face is guaranteed. CONCLUSIONS * (1) The

expression of the second invariant _J_2 of deviatoric stress at any point around the surrounding rock of circular roadway under non-uniform stress field is obtained. It is found that the

distribution of _J_2 under different stress environments will appear in three forms: ‘circular’, ‘oval’ and ‘butterfly’. * (2) The distribution pattern of the second invariant _J_2 of

deviatoric stress is closely related to the distribution pattern of plastic zone. When the distribution of surrounding rock _J_2 presents ‘circular’, ‘elliptical’ and ‘butterfly’, the

plastic zone presents a corresponding consistent shape. * (3) When the second invariant of deviatoric stress _J_2 generates stress concentration, the surrounding rock of roadway will produce

large-scale damage. When the degree of stress concentration is high, it may lead to the malignant expansion of surrounding rock of roadway. * (4) The distribution of the second invariant_

J_2 of deviatoric stress is directional. When the principal stress rotates over a certain angle, the second invariant _J_2 of deviatoric stress and plastic zone also rotate over the same

angle. * (5) Under the influence of superimposed mining, the second invariant deviatoric stress _J_2 in the wind lane of 160,206 working face in Yangchangwan presents a butterfly

distribution, and the stress butterfly leaves show a certain degree of rotation. Based on the failure form of plastic zone, the corresponding optimized support scheme is proposed, and the

engineering effect is well applied. DATA AVAILABILITY The datasets generated and/or analyzed during the current study are available from the corresponding author upon reasonable request.

REFERENCES * Peng, M. L., He, M. C., Xiao, Y. M., Cheng, T. & Qiao, Y. F. Asymmetric failure behavior of surrounding rock in the deep roadway: A semi-analytical solution. _Eng. Fail.

Anal._ 160, 108075. https://doi.org/10.1016/j.engfailanal.2024.108075 (2024). Article  MATH  Google Scholar  * Liu, H. T. et al. Nonlinear empirical failure criterion for rocks under

triaxial compression. _J. China Univ. Mining Technol._ 34(03), 351–369. https://doi.org/10.1016/j.ijmst.2024.03.002 (2024). Article  MATH  Google Scholar  * Liu, H. T. et al. Strength and

damage evolution mechanism of rock mass with holes under cyclic loading. _J. Cent. S. Univ._ 31, 2717–2735. https://doi.org/10.1007/s11771-024-5714-4 (2024). Article  MATH  Google Scholar  *

Liu, H. T. et al. Mechanism of non-uniform expansion and stability control in surrounding rock failure zone due to superimposed mining. _J. Mining Saf. Eng._ 41(03), 522–532.

https://doi.org/10.13545/j.cnki.jmse.2022.0355 (2024). Article  MATH  Google Scholar  * Liu, H. T. et al. Research on energy evolution law and control method of deformation of high stress

roadway surrounding rock. _J. China Coal Soc._ 1, 1–15. https://doi.org/10.13225/j.cnki.jccs.2023.1364 (2024). Article  MATH  Google Scholar  * Wu, X. Y. et al. Temporal-spatial evolutionary

law of plastic zone and stability control in repetitive mining roadway. _J. China Coal Soc._ 45(10), 3389–3400. https://doi.org/10.13225/j.cnki.jccs.2019.1051 (2020). Article  CAS  MATH 

Google Scholar  * Huang, B. X. et al. Large deformation theory of rheology and structural instability of the surrounding rock in deep mining roadway. _J. China Coal Soc._ 45(03), 911–926.

https://doi.org/10.13225/j.cnki.jccs.SJ19.1451 (2020). Article  Google Scholar  * Feng, G. Y. et al. Asymmetric deformation mechanism and control measures for mining roadway under roadway

under gob in close proximity. _J. China Univ. Mining Technol._ 51(04), 617–631. https://doi.org/10.13247/j.cnki.jcumt.001375 (2022). Article  Google Scholar  * Zhao, H. B. et al.

Distribution characteristics of deviatoric stress field and failure law of roadway surrounding rock under non-hydrostatic pressure. _J. China Coal Soc._ 46(02), 370–381.

https://doi.org/10.13225/j.cnki.jccs.2020.1877 (2021). Article  CAS  Google Scholar  * He, F. L. & Zhang, G. C. Stability analysis and control of deep underground roadways subjected to

high horizontal tectonic stress. _J. China Univ. Mining Technol._ 44(03), 466–476. https://doi.org/10.13247/j.cnki.jcumt.000345 (2015). Article  MATH  Google Scholar  * Wang, E. et al.

Distribution laws and control of deviatoric stress of surrounding rock in the coal roadway under intense mining. _J. Mining Saf. Eng._ 38(02), 276–285.

https://doi.org/10.13545/j.cnki.jmse.2020.0445 (2021). Article  MATH  Google Scholar  * Ma, N. J., Li, J. & Zhao, Z. Q. Distribution of the deviatoric stress field and plastic zone in

circular roadway surrounding rock. _J. China Univ. Mining Technol._ 44(02), 206–213. https://doi.org/10.13247/j.cnki.jcumt.000309 (2015). Article  MATH  Google Scholar  * Yu, W. J., Wu, G.

S., Yuan, C., Wang, P. & Du, S. H. Failure characteristics and engineering stability control of roadway surrounding rock based on deviatoric stress field. _J. China Coal Soc._ 42(06),

1408–1419. https://doi.org/10.13225/j.cnki.jccs.2016.1117 (2017). Article  MATH  Google Scholar  * Shi, H. Y. _Mechanics Mechanism and its Quantitative Analysis of the Formation of

Longmenshan Faults_ 42–43 (China University of Mining & Technology, 2021). MATH  Google Scholar  * Zheng, Y. T. Simplified model of three-dimensional stress field around borehole and

roadway. _J. China Coal Soc._ 4, 74–80. https://doi.org/10.13225/j.cnki.jccs.1982.04.008 (1982). Article  MATH  Google Scholar  * Shang, F. L. _Fundamentals of Plastic Mechanics_ (Xi’an

Jiaotong University Press, 2015). MATH  Google Scholar  * Xu, L. _Distribution and Application of Tloor Deviatoric Stress Tensor Invariants Under Close-Distance Multiple Pillars_ 11–13

(China University of Mining & Technology, 2014). MATH  Google Scholar  * Zhao, Z. Q. _Mechanism of Surrounding Rock Deformation and Failure and Control Method Research in Large

Deformation Mining Roadway_ 24–28 (China University of Mining & Technology, 2014). MATH  Google Scholar  * Zhao, Z. Q., Ma, N. J., Liu, H. T. & Guo, X. F. A butterfly failure theory

of rock mass around roadway and its application prospect. _J. China Univ. Mining Technol._ 47(05), 969–978. https://doi.org/10.13247/j.cnki.jcumt.000922 (2018). Article  CAS  MATH  Google

Scholar  * Guo, X. F., Ma, N. J., Zhao, X. D. & Li, Y. E. General shapes and criterion for surrounding rock mass plastic zone of round roadway. _J. China Coal Soc._ 41(8), 1871–1877.

https://doi.org/10.13225/j.cnki.jccs.2016.0787 (2016). Article  MATH  Google Scholar  * Li, J., Qing, X. B., Ma, N. J., Zhang, R. G. & Li, B. Formation mechanism and engineering

application of the directionality of butterfly leaf in the butterfly plastic zone of roadway rock surrounded. _J. China Coal Soc._ 46(09), 2838–2852.

https://doi.org/10.13225/j.cnki.jccs.2021.1150 (2021). Article  CAS  MATH  Google Scholar  * Huo, T. H. _Non-uniform Failure Mechanism and Stability Control of Mining Roadway Under

Deviatoric Stress Field_ (China University of Mining & Technology, 2022). MATH  Google Scholar  * Liu, H. T. et al. Low sensitivity research and engineering application of roadway

butterfly failure strength criterion. _Rock Soil Mech._ 45(01), 117–130. https://doi.org/10.27624/d.cnki.gzkbu.2022.000186 (2024). Article  MATH  Google Scholar  Download references

ACKNOWLEDGEMENTS This research was funded by the China Academy of Safety Production Science Basic Research Business Funding Special Funding (Grant Number: 2023JBKY12). AUTHOR INFORMATION

AUTHORS AND AFFILIATIONS * Institute of Mine Safety Technology, China Academy of Safety Science and Technology, Beijing, 100012, China Tianhong Huo, Shigen Fu, Botao Fu & Shouyin Wang *

School of Energy and Mining, China University of Mining and Technology (Beijing), Beijing, 100083, China Tianhong Huo & Hongtao Liu * Coal Industry Roadway Support and Disaster

Prevention Engineering Research Center, Beijing, 100083, China Hongtao Liu Authors * Tianhong Huo View author publications You can also search for this author inPubMed Google Scholar *

Hongtao Liu View author publications You can also search for this author inPubMed Google Scholar * Shigen Fu View author publications You can also search for this author inPubMed Google

Scholar * Botao Fu View author publications You can also search for this author inPubMed Google Scholar * Shouyin Wang View author publications You can also search for this author inPubMed 

Google Scholar CONTRIBUTIONS TH: conceptualization and methodology, HT: methodology and writing—original draft, SG and BT: supervision and conceptualization, and SY: investigation and data

curation. CORRESPONDING AUTHOR Correspondence to Tianhong Huo. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a

Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as

long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not

have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s

Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not

permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit

http://creativecommons.org/licenses/by-nc-nd/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Huo, T., Liu, H., Fu, S. _et al._ Non-uniform failure mechanism and stability

control of mining roadway under deviatoric stress field. _Sci Rep_ 15, 306 (2025). https://doi.org/10.1038/s41598-024-83355-x Download citation * Received: 04 September 2024 * Accepted: 13

December 2024 * Published: 02 January 2025 * DOI: https://doi.org/10.1038/s41598-024-83355-x SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content:

Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative KEYWORDS *

Surrounding rock control * Butterfly plastic zone * Deviatoric stress field * Second invariant of deviatoric stress * Roadway