Effective simulations of interacting active droplets

ABSTRACT Droplets form a cornerstone of the spatiotemporal organization of biomolecules in cells. These droplets are controlled using physical processes like chemical reactions and imposed

gradients, which are costly to simulate using traditional approaches, like solving the Cahn–Hilliard equation. To overcome this challenge, we here present an alternative, efficient method.

The main idea is to focus on the relevant degrees of freedom, like droplet positions and sizes. We derive dynamical equations for these quantities using approximate analytical solutions

obtained from a sharp interface limit and linearized equations in the bulk phases. We verify our method against fully-resolved simulations and show that it can describe interacting droplets

under the influence of chemical reactions and external gradients using only a fraction of the computational costs of traditional methods. Our method can be extended to include other

processes in the future and will thus serve as a relevant platform for understanding the dynamics of droplets in cells. SIMILAR CONTENT BEING VIEWED BY OTHERS SPONTANEOUS SELF-PROPULSION AND

NONEQUILIBRIUM SHAPE FLUCTUATIONS OF A DROPLET ENCLOSING ACTIVE PARTICLES Article Open access 14 April 2022 PHYSICOCHEMICAL HYDRODYNAMICS OF DROPLETS OUT OF EQUILIBRIUM Article 23 July 2020

DROPLET DUOS ON WATER DISPLAY PAIRING, AUTONOMOUS MOTION, AND PERIODIC ERUPTION Article Open access 31 July 2023 INTRODUCTION Phase separation has recently been recognized as a powerful

mechanism to organize biomolecules in the interior of biological cells1,2,3,4,5. The droplets that spontaneously form via phase separation allow cells to sort molecules into compartments,

which facilitates different functions, including controlling reactions6,7, storing molecules8, and buffering stochastic noise9. To control these processes, cells need to regulate phase

separation in space and time. Examples for control mechanisms include chemical gradients10,11,12,13, chemical modifications of the involved molecules14,15,16,17,18,19,20, and global

parameters, like pH and temperature21,22,23,24,25,26. Numerical simulations offer an attractive way to investigate these physical systems to understand how cells control their many droplets.

The dynamics of droplets are often simulated using the Cahn-Hilliard equation27,28,29. This fourth-order partial differential equation is typically expensive to simulate since it requires

fine spatial discretization and small time steps. Earlier approaches have improved the computational speed of numerical simulations of the Cahn–Hilliard equation using multi-grid methods30,

finite element modeling31,32, incorporating mesh-less methods33, and adaptive grids34,35, but the fundamental drawbacks still persist. Other approaches, such as Molecular Dynamics

simulations36,37 and Monte-Carlo methods38, have also been used to simulate phase separation, but are also computationally expensive since they resolve details that are often not necessary

for predicting the dynamics of droplets. In this paper, we present a fast and efficient numerical method for simulating the dynamics of many interacting droplets. The method is based on

analytical results from a thin-interface approximation of the continuous Cahn–Hilliard equation39. In our effective model, we describe only the dynamics of the necessary degrees of freedom,

which are the droplet positions and radii as well as some coarse information about the dilute phase. The interaction of the droplets via the dilute phase is captured by discretizing their

vicinity into thin annular sectors. The dynamics of droplet growth and drift follows from material fluxes exchanged between the droplet and the dilute phase, which are obtained from solving

a steady-state reaction–diffusion equation inside all sectors. We present the model by first introducing the basic thermodynamic principles of phase separation, then the analytical theory

behind the effective droplet model, and finally the details of the numerical method describing the dynamics of the droplets and dilute background. MODEL The main idea of our model is to

replace the detailed description of the entire concentration field by the relevant degrees of freedom of the droplets. We focus on the typical situation of well-separated droplets that are

spherical due to surface tension, and thus describe the droplets by their positions \(\varvec{x}_i\) and radii \(R_i\). To build up the theory systematically, we will next introduce the

continuous theory, the analytical description of isolated droplets, and then the full effective model. CONTINUOUS THEORY OF PHASE SEPARATION We consider an isothermal, incompressible fluid

in a closed system of volume \(V_\text{tot}\) that consists of solvent and droplet material. The composition is described by the volume fraction \(\phi (\varvec{x}, t)\) of the droplet

material, while the solvent volume fraction is given by \(1-\phi\). The thermodynamic state of the system is governed by the free energy functional \(F[\phi ] = \int \left( f(\phi ) +

\frac{\kappa }{2} \, |\varvec{\nabla } \phi | ^ 2 \right) \mathrm{d}V\); see ref.28, where \(\kappa\) is a parameter related to the interfacial tension, while phase separation is promoted by

the free energy density \(f(\phi )\). For simplicity, we here consider a polynomial form, $$\begin{aligned} f(\phi ) = \frac{b}{2}(\phi - \phi ^{0}_\text{out})^2(\phi - \phi

^{0}_\text{in})^2 \;, \end{aligned}$$ (1) where the minima \(\phi ^{0}_\mathrm{in}\) and \(\phi ^{0}_\text{out}\) are the equilibrium concentrations in a thermodynamically large system and

_b_ denotes the energy scale. The dynamics of the system follow from the continuity equation, \(\partial _t \phi + \varvec{\nabla } \cdot \varvec{j} = s\). Here, \(\varvec{j}\) denotes

spatial fluxes, which for simplicity will only be driven by diffusive processes, so hydrodynamic fluxes are neglected. Conversely, _s_ is a source term related to chemical reactions that

convert droplet material into solvent and vice versa39. Chemical reactions are typically local and often described by rate laws that depend on composition. Conversely, the non-local

diffusive fluxes \(\varvec{j}\) are driven by gradients in chemical potential $$\begin{aligned} \mu = \nu \frac{\delta F}{\delta \phi } = b (\phi ^{0}_\mathrm{in} - \phi ) (\phi

^{0}_\mathrm{out} - \phi ) (2\phi - \phi ^{0}_\mathrm{in} - \phi ^{0}_\mathrm{out}) - \kappa \varvec{\nabla }^2 \phi \;, \end{aligned}$$ (2) where \(\nu\) is the molecular volume of the

droplet material. Linear non-equilibrium thermodynamics implies \(\varvec{j} = -\Lambda (\phi ) \varvec{\nabla }\mu\), where \(\Lambda (\phi )\) is a positive mobility40. Hence,

$$\begin{aligned} \frac{\partial \phi }{\partial t} = \varvec{\nabla } \cdot [\Lambda (\phi ) \varvec{\nabla } \mu ] + s(\phi ) \;, \end{aligned}$$ (3) is a fourth-order, non-linear partial

differential equation requiring two boundary conditions. We here focus on the typical choice of no-flux conditions (\(\varvec{n} \cdot \varvec{\nabla } \mu = 0\)) and that solvent and

droplet material interact identically with the system’s boundaries (\(\varvec{n} \cdot \varvec{\nabla } \phi = 0\)), where \(\varvec{n}\) denotes the normal vector at the boundary. In the

case without chemical reactions (\(s=0\)), Eq. (3) reduces to the seminal Cahn–Hilliard equation28, which describes passive phase separation. In particular, two bulk phases with composition

\(\phi ^{0}_\mathrm{in}\) and \(\phi ^{0}_\mathrm{out}\) typically emerge. These phases are separated by an interface of width \(w = 2\sqrt{\kappa / b}\) with surface tension \(\gamma =

\frac{1}{6} \sqrt{b \kappa }\)27,39. When chemical reactions are weak, this general structure is typically preserved, although long-term dynamics, like Ostwald ripening, can be strongly

modified39. Strong chemical reactions can actually destroy droplets39 and they might also lead to more complicated patterns41,42, which go beyond the scope of this paper. Instead, we here

focus on situations where well-defined droplets with a thin interface are typical. The dynamics given by Eq. (3) adequately describe phase separation, but it can be prohibitively costly to

simulate due to multiple reasons: (1) The interface needs to be resolved, implying discretizations on the order of the typically small interface width _w_. (2) The equation contains

fourth-order derivatives in space, which often limits the time steps. (3) Interesting dynamics often take place on very long time scales. For instance, during Ostwald ripening43,44, length

scales in the system evolve as \(t^{ 1/3}\), requiring long simulations to capture relevant behaviour. However, since we are interested primarily in modelling dynamics of droplets, we

circumvent these problems by focusing only on phase separation inside the nucleation and growth regime of the free energy density, and assume that sufficiently finite perturbations have

already nucleated droplets. We employ the thin-interface approximation39, which is a coarse-grained analytical formulation of the continuous model Eq. (3) valid when the system is subject to

strong phase separation, low variation of volume fractions in the droplet phase and the dilute phase, and large droplet sizes compared to the interface width. This analytical approach was

utilized earlier to study kinetics of many-droplet systems and effects of chemical reactions on such systems39. In the next section, we elaborate on using the thin-interface approximation to

build an effective droplet model describing the dynamics of droplets and dynamics of the dilute phase separately, instead of the full volume fraction field from the continuous model, thus

effectively ‘de-coupling’ the description of phase separated droplets from the dilute phase. EFFECTIVE DESCRIPTION OF ISOLATED DROPLETS To build the effective model, we next derive

approximate descriptions of the dynamics of the radius _R_ and position \(\varvec{x}\) of an isolated droplet. Since we only consider spherical droplets with a thin interface (\(R \gg w\))

and weak chemical reactions, we can use basic thermodynamics to derive the equilibrium concentrations inside and outside of the interface of the droplet, denoted by \(\phi

^\mathrm{eq}_\mathrm{in}\) and \(\phi ^\mathrm{eq}_\mathrm{out}\), respectively. Due to surface tension effects, they are slightly elevated above the basal values \(\phi ^0_\mathrm{in}\) and

\(\phi ^0_\mathrm{out}\) prescribed by the free energy density; see Eq. (1). To first order in the curvature of the surface, we have $$\begin{aligned} \phi ^\mathrm{eq}_\mathrm{in}&=

\phi ^{0}_\mathrm{in} \left( 1 + \frac{l_{\gamma , \mathrm{in}}}{R} \right) \qquad \text {and} \end{aligned}$$ (4a) $$\begin{aligned} \phi ^\mathrm{eq}_\mathrm{out}&= \phi

^{0}_\mathrm{out} \left( 1 + \frac{l_{\gamma , \mathrm{out}}}{R}\right) \;, \end{aligned}$$ (4b) where \(l_{\gamma , \mathrm{out}}\) and \(l_{\gamma , \mathrm{in}}\) are capillary lengths27.

In our case they read \(l_{\gamma , \mathrm{in}} = (\kappa /b)^{1/2} /[3 \phi ^{0}_\mathrm{in} \left( \phi ^{0}_\mathrm{in} - \phi ^{0}_\mathrm{out}\right) ^{3}]\) and \(l_{\gamma ,

\mathrm{out}} = (\kappa /b)^{1/2}/[3 \phi ^{0}_\mathrm{out} \left( \phi ^{0}_\mathrm{in} - \phi ^{0}_\mathrm{out}\right) ^{3}]\) in three dimensions. The dynamics of the volume fraction

field \(\phi _\mathrm{in}\) inside the droplet is in principle described by Eq. (3), but since the composition typically hardly varies, we can linearize \(\phi _\mathrm{in}\) around \(\phi

^{0}_\mathrm{in}\) to obtain $$\begin{aligned} \frac{\partial \phi _\mathrm{in}}{\partial t} \approx D_\mathrm{in} \varvec{\nabla } ^2 \phi _\mathrm{in} + s(\phi ^{0}_\mathrm{in}) -

k_{\mathrm{in}}(\phi _\mathrm{in} - \phi ^{0}_\mathrm{in}) \;, \end{aligned}$$ (5) where \(D_\mathrm{in} = \Lambda (\phi ^0_\mathrm{in}) \, b\) is the diffusivity and \(k_{\mathrm{in}}= -

s'(\phi ^{0}_\mathrm{in})\) denotes the reaction rate27. Generally, positive rates (\(k_\mathrm{in}>0\)) stabilize the volume fraction \(\phi _\mathrm{in}\), while negative rates

might destabilize it. However, the instability is suppressed when the droplet radius _R_ is small compared to the reaction–diffusion length scale, \(\xi

_\mathrm{in}=\sqrt{D_\mathrm{in}/|k_{\mathrm{in}}|}\)27. Since we here consider weak chemical reactions, \(\xi _\mathrm{in}\) will be large, and we thus assume \(R \ll \xi _\mathrm{in}\) in

the following. We use this to solve Eq. (5) in stationary state in a system with angular symmetry using the boundary conditions \(\phi _\mathrm{in}(R) = \phi ^\mathrm{eq}_\mathrm{in}\) and

\(\partial _r \phi _\mathrm{in}(0) = 0\). The analytical result allows us to estimate the diffusive flux \(\varvec{j}_\mathrm{in}\) inside the interface, $$\begin{aligned}

\varvec{j}_\mathrm{in} \approx \frac{R}{d} s(\phi ^\mathrm{eq}_\mathrm{in})\,\varvec{n} \;, \end{aligned}$$ (6) where _d_ is the space dimension; see Supporting Information, Section III.

Production of droplet material inside the droplet (\(s(\phi ^\mathrm{eq}_\mathrm{in}) > 0\)) leads to an outward flux \(\varvec{j}_\mathrm{in} \cdot \varvec{n} > 0\), which can drive

droplet growth. Conversely, destroying droplet material (\(s(\phi ^\mathrm{eq}_\mathrm{in}) < 0\)) promotes shrinking droplets. Droplets might also grow if they take up material from the

surrounding. Similarly to inside of droplets, the volume fraction \(\phi _\mathrm{out}\) will typically vary only little, so we can linearize around the base value \(\phi ^0_\mathrm{out}\)

to obtain the reaction–diffusion equation $$\begin{aligned} \frac{\partial \phi _\mathrm{out}}{\partial t} \approx D_\mathrm{out} \varvec{\nabla } ^2 \phi _\mathrm{out}+ s(\phi

_\mathrm{out}) \;, \end{aligned}$$ (7) where \(D_\mathrm{out} = \Lambda (\phi ^0_\mathrm{out}) \, b\) is the diffusivity outside droplets. Solving this equation and obtaining the

corresponding flux \(\varvec{j}_\mathrm{out}\) outside the droplet is more difficult since the environment of the droplet might not be isotropic. We thus discuss the coupling of droplets to

the dilute phase \(\phi _\mathrm{out}\) in more detail in the next section. If we know the fluxes \(\varvec{j}_\mathrm{in}\) and \(\varvec{j}_\mathrm{out}\), we can determine the net

accumulation of droplet material at the interface, which implies droplet growth. Note that only the normal components of the fluxes affect the shape, while the tangential components merely

distribute material parallel to the interface. The shape changes of an isolated droplet are thus described by the interfacial speed \(v_\mathrm{n}\) in the normal direction27,

$$\begin{aligned} v_\mathrm{n}\approx \frac{\varvec{j}_\mathrm{in}- \varvec{j}_\mathrm{out}}{\phi ^\mathrm{eq}_\mathrm{in}- \phi ^\mathrm{eq}_\mathrm{out}} \cdot \varvec{n} \;;

\end{aligned}$$ (8) see Supporting Information, Section I. General shape changes can result in non-spherical droplets, but since surface tension effects typically ensure a near-spherical

shape, we project the general shape onto the degrees of freedom that we use to describe the droplet, $$\begin{aligned} \frac{\mathrm{d}R}{\mathrm{d}t}&= \frac{1}{S} \int v_\mathrm{n}\,

\mathrm{d}A \qquad \text {and} \end{aligned}$$ (9a) $$\begin{aligned} \frac{\mathrm{d} \varvec{x}}{\mathrm{d}t}&= \frac{d}{S} \int v_\mathrm{n}\, \varvec{n} \, \mathrm{d}A \;,

\end{aligned}$$ (9b) where the integral is over the droplet surface, _d_ is the space dimension, and _S_ is the surface area of the droplet; see Supporting Information, Section II. Here, the

first equation describes how material accumulates at the interface due to sum of all normal fluxes \(v_\mathrm{n}\), leading to growth. The second equation describes how the weighted sum of

all vectorial fluxes gives rise to drift. Taken together, Eq. (9) determines how an isolated droplet evolves in time. This involves Eqs. (4), (6), (8) as well as an approximation for the

fluxes \(\varvec{j}_\mathrm{out}\) outside the droplet interface, which is the central part of our method that we discuss next. NUMERICAL MODEL FOR MANY DROPLETS The dynamics of many

droplets in the same system are coupled since they may exchange material via the dilute phase. To describe this exchange, and ultimately derive the flux \(\varvec{j}_\mathrm{out}\) at each

droplet, we first consider the dynamics of the volume fraction of the dilute phase \(\phi _\mathrm{out}\). In principle, the dynamics of \(\phi _\mathrm{out}\) follows from Eq. (7), with

appropriate boundary conditions applied at the system’s boundary and at all droplet surfaces. To simplify the description of the dilute phase, we assume that \(\phi _\mathrm{out}\) is

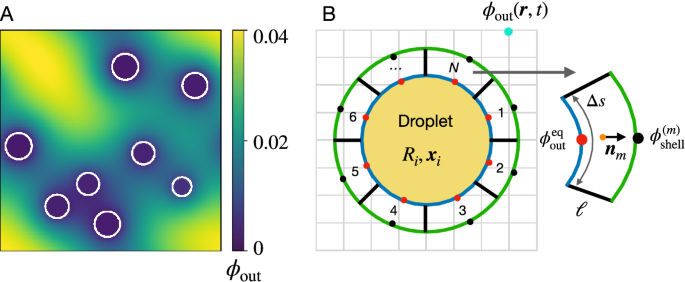
defined in the entire system, including where droplets are; see Fig. 1A. In this picture, droplets are local perturbations that exchange material with the background field \(\phi

_\mathrm{out}\). DYNAMICS OF THE BACKGROUND FIELD The background field \(\phi _\mathrm{out}\) changes due to diffusion and reactions, even if droplets are absent. To capture this dynamics,

we discretize the continuous field \(\phi _\mathrm{out}\) on a uniform Cartesian grid with a distance \(\Delta x\) between the neighbouring support points. We then evolve Eq. (7) in time

using finite central differences and explicit temporal stepping45. Since we do not need to resolve droplets at this scale, the spatial discretization can be much larger than in traditional

Cahn–Hilliard equations. GROWTH OF A SINGLE DROPLET IN A BACKGROUND FIELD To obtain the flux \(\varvec{j}_\mathrm{out}\) in the vicinity of an isolated droplet, we need to determine \(\phi

_\mathrm{out}\) in the region surrounding this droplet. We do this by considering Eq. (7) in an annular shell of thickness \(\ell\) surrounding the droplet, which we further discretize into

_N_ sectors in the angular dimensions; see Fig. 1. In two-dimensional systems, we place sectors of equal size uniformly around the circle. Such symmetric placement is impossible in three

dimensions, where we instead place _N_ points approximately uniformly on the sphere and use a spherical Voronoi tessellation 46 to determine the corresponding sectors. In both cases, we

assume that fluxes in the angular directions are negligible for simplicity, so we can express the volume fraction in the _m_-th sector as \(\phi _\mathrm{out}^{(m)}(r)\), where _r_ is a

radial coordinate measuring distance from the droplet position \(\varvec{x}\). We determine \(\phi _\mathrm{out}^{(m)}(r)\) using Eq. (7) in stationary state with the boundary conditions

\(\phi _\mathrm{out}^{(m)}(R)=\phi ^\mathrm{eq}_\mathrm{out}\) and \(\phi _\mathrm{out}^{(m)}(R + \ell )= \phi _\mathrm{shell}^{(m)}\). Here, \(\phi _\mathrm{shell}^{(m)}\) is the volume

fraction of droplet material in the background field at the outer side of the _m_-th shell sector, which we estimate from a linear interpolation of the discretized background field \(\phi

_\mathrm{out}\); see Fig. 1. Since \(\phi _\mathrm{out}^{(m)}(r)\) typically varies only marginally in the shell sector, we also linearize the reaction flux, \(s(\phi _\mathrm{out}^{(m)})

\approx \Gamma _\mathrm{out} - k_\mathrm{out}\, \phi _\mathrm{out}\), by imposing \(s(\phi _\mathrm{out}^{(m)})(R) = s(\phi ^\mathrm{eq}_\mathrm{out})\) and \(s(\phi _\mathrm{out}^{(m)})(R +

\ell ) = s(\phi _\mathrm{shell}^{(m)})\). This implies \(\Gamma _\mathrm{out} = [\phi _\mathrm{shell}^{(m)} \, s(\phi ^\mathrm{eq}_\mathrm{out}) - \phi ^\mathrm{eq}_\mathrm{out}\, s(\phi

_\mathrm{shell}^{(m)})] / (\phi _\mathrm{shell}^{(m)} - \phi ^\mathrm{eq}_\mathrm{out})\) and \(k_\mathrm{out}= [s(\phi ^\mathrm{eq}_\mathrm{out}) - s(\phi _\mathrm{shell}^{(m)})] / (\phi

_\mathrm{shell}^{(m)} - \phi ^\mathrm{eq}_\mathrm{out})\). Taken together, we obtain an analytical approximation of \(\phi _\mathrm{out}^{(m)}(r)\) in each shell sector, from which we

determine the local normal flux \(\varvec{j}_\mathrm{out}^{(m)}\) outside the droplet; see Supporting Information, Section IV. Using these expressions together with Eqs. (6), (8) and (9), we

find that individual droplets evolve according to $$\begin{aligned} \frac{\mathrm{d}R}{\mathrm{d}t}&\approx \frac{1}{\phi ^\mathrm{eq}_\mathrm{in}} \sum _{m=1}^{N} \frac{A_m}{S}\left(

\frac{R}{d} s(\phi ^\mathrm{eq}_\mathrm{in}) - {j}^{(m)}_\mathrm{out} \right) \qquad \text {and} \end{aligned}$$ (10a) $$\begin{aligned} \frac{\mathrm{d}\varvec{x}}{\mathrm{d}t}&\approx

\frac{d}{\phi ^\mathrm{eq}_\mathrm{in}} \sum _{m=1}^{N} \frac{A_m}{S} \left( \frac{R}{d}s(\phi ^\mathrm{eq}_\mathrm{in}) - {j}^{(m)}_\mathrm{out}\right) \varvec{n}_m \;, \end{aligned}$$

(10b) where _R_ and _S_ are radius and surface area of the droplet, respectively, \(A_m\) is the inner area of the shell sector and \(\varvec{n}_m\) is the unit vector pointing from the

droplet center to the _m_-th shell center; see Fig. 1. We use Eq. (10) to describe how internal reactions and external material exchange with the background affects the dynamics of each

droplet. COUPLED DYNAMICS OF DROPLETS AND THE BACKGROUND FIELD Equation (10) describe how droplets change when they exchange droplet material with the background field \(\phi

_\mathrm{out}\). Due to material conservation, the material flux from the droplet toward each sector _m_, \(\varvec{j}_\mathrm{out}^{(m)} \cdot \varvec{n} \, A_m\), needs to accumulate in

the background field. We use a linear interpolation at the midpoint of the inner boundary of the shell section (red points in Fig. 1B) to add the respective amount to the background field

\(\phi _\mathrm{out}\). Note that negative fluxes \(\varvec{j}_\mathrm{out}^{(m)}\) distribute material from the background field to the droplet and thus lead to growth. Taken together, this

procedure ensures material conservation while preserving anisotropies of the exchange. FULL SIMULATION The full numerical method evolves the state of the system, i.e., the discretized

background field \(\phi _\mathrm{out}(\varvec{r})\) and the positions \(\varvec{x}_i\) and radii \(R_i\) of all droplets, in time. We propose an explicit iteration, where the state at

\(t+\Delta t\) is directly determined from the state at time _t_. Here, we first evolve the reaction–diffusion equation Eq. (7) of the background field and then iterate over all droplets.

For each droplet, we determine the fluxes \(\varvec{j}_\mathrm{out}^{(m)} \cdot \varvec{n}\) for all shell sectors _m_ and remove the associated material from the background field. We then

update the droplet’s position and radius according to Eq. (10). Starting from an initial state at \(t=0\), this algorithm allows us to evolve the dynamics forward in time. CHOOSING

SIMULATION PARAMETERS The algorithm described above has several parameters that need to be chosen wisely for an accurate and fast simulation. In particular, we need to specify the

discretization \(\Delta x\) of the background field, the shell thickness \(\ell\), the typical size \(\Delta s\) of a shell sector, and the time step \(\Delta t\). We next discuss suitable

values for all four parameters using detailed simulation of the continuous model given by Eq. (3) as ground truth. We later show that the resulting choice for the parameters can recapitulate

many effects that have been described previously in the literature. To calibrate the simulation parameters, we compare our effective model to the established continuous model given by Eq.

(3). Our test case consists of two passive droplets of initial radius \(R_0=20 w\) whose centers are separated by \(S_\mathrm{d}=10 R_0\). The droplets are placed in a background of

vanishing initial volume fraction, \(\phi _\mathrm{out}(\varvec{r}, 0) = 0\), so the system is under-saturated and the droplets will shrink. For the continuous model, we exploit the angular

symmetry of the problem and consider an azimuthally symmetric cylindrical domain where \(r,z \in [0, 682 w]\). Conversely, our effective model is simulated in a 3-dimensional cubic domain of

size \([0, 1000 w]^{3}\). We compare the final radii of the droplets after a duration _T_, where the droplets typically have shrunk by about \(20\%\). The deviation of the mean droplet

radius \(\langle R_*\rangle\) of our effective model compared to the radius \(\langle R_\mathrm{CM}\rangle\) of the continuous model allows us to determine the crucial simulation parameters

\(\Delta x\), \(\ell\), and \(\Delta s\). GRID DISCRETIZATION \(\DELTA X\) The spatial discretization \(\Delta x\) determines the resolution at which variations of the background field

\(\phi _\mathrm{out}\) are resolved. Consequently, the choice of \(\Delta x\) is based on the problem: If spatial interactions are negligible and a mean-field model is desired, \(\Delta x\)

can be arbitrarily large. Conversely, if spatial correlations between droplets are important, \(\Delta x\) needs to be smaller than the droplet separation. Another case are external

gradients that affect droplets12, where \(\Delta x\) needs to be on the order of the droplet radii, so spatial anisotropies can be resolved on the droplet level. ANNULAR SHELL THICKNESS

\(\ELL\) The most crucial part of our numerical method describes how material exchanges between the droplets and the background field. To describe this exchange faithfully, we interpolate

the background field in an annular shell around the droplet. The thickness \(\ell\) of this shell can thus be interpreted as an interpolation length scale and its value affects the accuracy

of the simulation: If \(\ell \ll \Delta x\), the fluxes \(\varvec{j}_\mathrm{out}^{(m)}\) are overestimated since they scale with \(\ell ^{-1}\); see Supporting Information, Section IV.

Conversely, if \(\ell \gg \Delta x\), the background field would not be evaluated in the vicinity of the droplet, so interactions cannot be captured correctly. Taken together, we conclude

that \(\ell \sim \Delta x\) is a reasonable choice for the shell thickness. Indeed, Fig. 2A shows that this choice leads to a faithful estimate of the droplet growth for various values of

\(\Delta x\). SHELL SECTOR WIDTH \(\DELTA S\) To resolve spatial anisotropies around a droplet, we discretize the shell into _N_ sectors; see Fig. 1B. To obtain \(\phi _\mathrm{shell}\) for

each sector, the background field \(\phi _\mathrm{out}\) is interpolated once per sector. Consequently, a larger number of sectors leads to a finer discretization and potentially a higher

accuracy at the expense of larger computational cost. However, the accuracy is limited by the background discretization \(\Delta x\) as increasing _N_ will have hardly any benefit if the

distance \(\Delta s\) between interpolation points is already smaller than \(\Delta x\). For two and three dimensions, we respectively use \(\Delta s\approx 2\pi R/N\) and \(\Delta s\approx

\sqrt{4 \pi R^2 / N}\); see Fig. 1B. Using \(\Delta s\sim \Delta x\), we can solve these equations for _N_, so that we can determine the number of sectors for each droplet based on its

instantaneous radius \( R \). Note that this implies that the dynamics of larger droplets will be described by more sectors to faithfully capture the interaction with their surrounding. Fig.

2B shows that the shell sector size \(\Delta s\) has only marginal effects in simple situations. TIME STEP \(\DELTA T\) While the three previously discussed parameters affect material

fluxes between droplets and background, the time step \(\Delta t\) determines the accuracy of dynamics of the model. Smaller values of \(\Delta t\) imply more accurate simulations, while

larger values result in faster simulations, although numerical instabilities might also render simulations unstable. We next separately analyze the dynamics of the background field, the

shell, and the droplet growth to identify the maximal suitable value of \(\Delta t\). The dynamics of the background are described by the partial differential equation Eq. (7), which we here

solve using a simple explicit Euler scheme. A standard von Neumann stability analysis shows that this scheme is stable if \(\Delta t< \Delta x^2/(2 D_\mathrm{out})\), where

\(D_\mathrm{out}\) is the diffusivity in the background field. Consequently, a suitable time step for evolving the background field is \(\Delta t_\mathrm{background} = 0.1 \Delta

x^2/D_\mathrm{out}\), where we chose the constant pre-factor conservatively. Similarly, we define \(\Delta t_\mathrm{shell} = 0.1 \ell ^2/D_\mathrm{out}\) for the shell. To ensure faithful

dynamics of droplet growth, we demand that the relative growth \(R^{-1}|\mathrm{d}R/\mathrm{d}t|\) is small during a single time step \(\Delta t\). Assuming that typical droplets are not

much smaller than the mean initial droplet radius \(\langle R\rangle\), this implies a maximal time step \(\Delta t_\mathrm{drop} = 0.1 \langle R\rangle ^2/D_\mathrm{out}\). Finally, we also

consider the time scale of reactions, \(\Delta t_\mathrm{reaction} = 0.1 / (\max _\phi |s(\phi )|)\), based on the maximal rate of \(s(\phi _\mathrm{out})\). Taken together, we set the time

step of the simulation to the minimal value of the four limiting time scales determined above. VALIDATION We showed above that \(\Delta x \approx \ell \approx \Delta s\) is a sensible

choice for the parameters of our algorithm. To see how this choice affects accuracy and speed of the simulation, we next present three simulation scenarios, which range from single droplets

in an heterogeneous environment to coarsening of large dilute emulsions. PASSIVE DROPLET IN EXTERNAL GRADIENT We first consider a single droplet in an external composition gradient, which is

maintained via boundary conditions. Biological cells use such a setup to control the position of droplets in their interior10,12,47. Fig. 3 shows that the effective droplet model captures

the drift and growth of the passive droplet quantitatively. While the resulting dynamics are very similar, the run time of the simulations are very different: The continuous model took

roughly one day to complete, while the effective model finished within 10 seconds on identical hardware. Since the continuous model is much slower, we performed some tests in the subsequent

sections only with the effective model. ACTIVE DROPLET WITH LOGISTIC GROWTH We next test whether our effective model also captures the growth of droplets subjected to non-linear chemical

reactions. We here consider logistic growth, \(s(\phi )= k \phi (1 - a \phi )\), where _k_ sets the reaction rate and _a_ determines the chemical equilibrium; the parameter \(a^{-1}\) is

often called the carrying capacity. In a phase separating system, these reactions produce droplet material outside the droplet (where \(\phi < a^{-1}\)) and destroy it inside (assuming

\(\phi ^{0}_\mathrm{out} > a^{-1}\)). These reactions are thus qualitatively similar to the active droplets with linear chemical reactions that we discussed above. However, the non-linear

chemical reactions now lead to a non-monotonous growth of the active droplet; see Fig. 4. Our effective model captures this intricate behaviour quantitatively; the deviations to the full

simulation of the continuous model are small. Taken together, our effective model adequately describes the behaviour of single active droplets, even if the chemical reactions are non-linear.

MEAN-FIELD COARSENING OF PASSIVE DROPLETS We next consider the interactions of many passive droplets in a dilute emulsion. When droplets only interact via the spatially averaged background

field, Lifshitz and Slyozov predicted that the average droplet radius \(\left\langle R \right\rangle\) grows as \(t^{1/3}\) in this case43,44,48. Our simulation of \(10^5\) droplets indeed

recovers this scaling (Fig. 5A) when we mimic this situation by setting the discretization \(\Delta x\) to the system size. Moreover, Fig. 5B shows that the distribution of radii also

follows the universal shape \(H(\rho ) = \frac{4}{9}\rho ^2\left( 1+ \frac{\rho }{3} \right) ^ {-7/3} \left( 1-\frac{2 \rho }{3} \right) ^{-11/3} \mathrm{exp} \left( 1 - \frac{3}{3 - 2\rho }

\right)\), where \(\rho =R/{\left\langle R \right\rangle }\) is a scaled droplet size43. Our effective model thus faithfully captures the dynamics of many droplets, optionally even beyond

the Lifshitz-Slyozov regime by increasing the spatial resolution to capture correlations in droplet growth. MEAN-FIELD COARSENING OF ACTIVE DROPLETS As a final example, we consider the

interaction of many active droplets in a dilute emulsion. Here, we focus on the simplest case of a first-order reaction between the solvent and the droplet material, which is known to

suppress Ostwald ripening27,39. We thus solve Eq. (3) using the reaction flux \(s(\phi ) = k_\mathrm{f}(1 - \phi ) - k_\mathrm{b}(\phi )\). Fig. 6 shows that the emulsions with broad initial

sizes quickly converge to mono-disperse distributions in 2 and 3 dimensions. The droplet size in stationary state is very close to the theoretical prediction, which we obtain numerically

from the condition \(\varvec{j}_\mathrm{in}= \varvec{j}_\mathrm{out}\) using Eqs. (5) and (7). Taken together, we thus demonstrated that our effective model faithfully recovers important

physical behaviour of active droplets. OUTLOOK AND DISCUSSION We showed that our effective method is orders of magnitudes faster than the continuous model while still accurately capturing

the dynamics of droplets under the influence of chemical reactions and external gradients. To demonstrate that the method also extends to more challenging situations, we finally simulate the

combination of chemical reactions and external gradients on the dynamics of the droplets. Fig. 7 shows that droplets grow as they drift along the gradient and they approach the fixed radius

given by \(\overline{R}_\mathrm{3D}\), so that this system controls droplet drift and size. Taken together, our simulations demonstrate that the novel simulation method captures the

dynamics of interacting active droplets efficiently. To gain the significant speed-up, our approach focuses on relevant degrees of freedom and leverages analytical results. This method can

in principle be extended to more challenging situations in the future. For instance, droplets embedded in an elastic matrix affect each others growth, which can be described by similar

effective theories49,50. Similar dynamics will also inform the dynamics of droplets in cells, where for instance chromatin and the cytoskeleton suppress coalescence of condensates51,52,53.

Our method can in principle also account for fluid flows, which are present in many liquid-like systems 10,54,55. Here, large scale flows will advect the droplets and also affect the

background field. Finally, we could account for Brownian motion of droplets, their coalescence upon contact, and their spontaneous division in sufficiently strongly driven systems 56,57. In

particular, droplets have shown anomalous coarsening behavior in cells, primarily due to hindrance and physical barriers which curb their ability of coalesce51,52,58,59. Extending our

effective method to account for these physical processes will allow analyzing more and more complex situations, approaching the complexity necessary to understand the behavior of many

droplets in biological cells. In summary, we have demonstrated that our effective method faithfully captures the effects of chemical reactions and external chemical gradients. The method is

several orders of magnitude faster than traditional continuous models, making it viable for fast and computationally efficient simulations of systems with many droplets. More importantly,

our model provides a modular platform, which can be extended with other relevant physical phenomena affecting droplets, thus shedding insights on the formation, dissolution, stability, and

sizes of biomolecular condensates. DATA AVAILABILITY The source code of the project is freely available under the https://doi.org/10.5281/zenodo.7337474 and

https://github.com/zwicker-group/agent-based-emulsions. The datasets generated during the current study are available under the https://doi.org/10.5281/zenodo.7372489. REFERENCES * Keating,

Christine D. & Pappu, Rohit V. Liquid-liquid phase separation: A widespread and versatile way to organize aqueous solutions. _J. Phys. Chem. B_ 125(45), 12399–12400 (2021). Article  CAS

  Google Scholar  * Mitrea, Diana M. & Kriwacki, Richard W. Phase separation in biology; Functional organization of a higher order. _Cell Commun. Signal._ 14(1), 1 (2016). Article 

Google Scholar  * Banani, Salman F., Lee, Hyun O., Hyman, Anthony A. & Rosen, Michael K. Biomolecular condensates: Organizers of cellular biochemistry. _Nat. Rev. Mol. Cell Biol._ 18(5),

285–298 (2017). Article  CAS  Google Scholar  * Hyman, Anthony A., Weber, Christoph A. & Jülicher, Frank. Liquid-liquid phase separation in biology. _Ann. Rev. Cell Dev. Biol._ 30(1),

39–58 (2014). Article  CAS  Google Scholar  * Lyon, Andrew S., Peeples, William B. & Rosen, Michael K. A framework for understanding the functions of biomolecular condensates across

scales. _Nat. Rev. Mol. Cell Biol._ 22(3), 215–235 (2021). Article  CAS  Google Scholar  * Andersson, I. & Backlund, A. Structure and function of rubisco. _Plant Physiol. Biochem._

46(3), 275–291 (2008). Article  CAS  Google Scholar  * Mingjian, Du. & Chen, Zhijian J. Dna-induced liquid phase condensation of cgas activates innate immune signaling. _Science_

361(6403), 704–709 (2018). Article  Google Scholar  * Greenblatt, Ethan J. & Spradling, Allan C. Fragile x mental retardation 1 gene enhances the translation of large autism-related

proteins. _Science_ 361(6403), 709–712 (2018). Article  ADS  CAS  Google Scholar  * Klosin, A. _et al._ Phase separation provides a mechanism to reduce noise in cells. _Science_ 367(6476),

464–468 (2020). Article  ADS  CAS  Google Scholar  * Brangwynne, Clifford P. _et al._ Germline p granules are liquid droplets that localize by controlled dissolution/condensation. _Science_

324(5935), 1729–1732 (2009). Article  ADS  CAS  Google Scholar  * Saha, Shambaditya _et al._ Polar positioning of phase-separated liquid compartments in cells regulated by an mrna

competition mechanism. _Cell_ 166(6), 1572-1584.e16 (2016). Article  CAS  Google Scholar  * Weber, Christoph A., Lee, Chiu Fan & Jülicher, Frank. Droplet ripening in concentration

gradients. _New J. Phys._ 19(5), 053021 (2017). Article  ADS  Google Scholar  * Youjun, Wu. _et al._ Rapid diffusion-state switching underlies stable cytoplasmic gradients in the

Caenorhabditis elegans zygote. _Proc. Natl. Acad. Sci._ 115(36), E8440–E8449 (2018). Google Scholar  * Hofweber, Mario & Dormann, Dorothee. Friend or foe–post-translational modifications

as regulators of phase separation and rnp granule dynamics. _J. Biol. Chem._ 294(18), 7137–7150 (2019). Article  CAS  Google Scholar  * Ryan, Veronica H. _et al._ Mechanistic view of

hnrnpa2 low-complexity domain structure, interactions, and phase separation altered by mutation and arginine methylation. _Mol. Cell_ 69(3), 465-479.e7 (2018). Article  CAS  Google Scholar 

* Qamar, Seema _et al._ Fus phase separation is modulated by a molecular chaperone and methylation of arginine cation-\(\pi\) interactions. _Cell_ 173(3), 720-734.e15 (2018). Article  CAS 

Google Scholar  * Nott, Timothy-J.. _et al._ Phase transition of a disordered nuage protein generates environmentally responsive membraneless organelles. _Mol. Cell_ 57(5), 936–947 (2015).

Article  CAS  Google Scholar  * Zwicker, David, Decker, Markus, Jaensch, Steffen, Hyman, Anthony A. & Jülicher, Frank. Centrosomes are autocatalytic droplets of pericentriolar material

organized by centrioles. _Proc. Natl. Acad. Sci._ 111(26), E2636–E2645 (2014). Article  ADS  CAS  Google Scholar  * Söding, Johannes, Zwicker, David, Sohrabi-Jahromi, Salma, Boehning, Marc

& Kirschbaum, Jan. Mechanisms for active regulation of biomolecular condensates. _Trends Cell Biol._ 30(1), 4–14 (2020). Article  Google Scholar  * Kirschbaum, Jan & Zwicker, David.

Controlling biomolecular condensates via chemical reactions. _J. R. Soc. Interface_ 18(179), 20210255 (2021). Article  CAS  Google Scholar  * Orij, Rick, Brul, Stanley & Smits, Gertien 

J. Intracellular pH is a tightly controlled signal in yeast. _Biochimica et Biophysica Acta (BBA) Gen. Subjects_ 1810(10), 933–944 (2011). Article  CAS  Google Scholar  * Kroschwald, Sonja

_et al._ Different material states of pub1 condensates define distinct modes of stress adaptation and recovery. _Cell Rep._ 23(11), 3327–3339 (2018). Article  CAS  Google Scholar  * Peters,

Lee Zeev, Hazan, Rotem, Breker, Michal, Schuldiner, Maya & Ben-Aroya, Shay. Formation and dissociation of proteasome storage granules are regulated by cytosolic pH. _J. Cell Biol._

201(5), 663–671 (2013). Article  CAS  Google Scholar  * Petrovska, I., Nüske, E., Munder, M. C., Kulasegaran, G., Malinovska, L., Kroschwald, S., Richter, D., Fahmy, K., Gibson, K.,

Verbavatz, J.-M., & Alberti S. (2014) Filament formation by metabolic enzymes is a specific adaptation to an advanced state of cellular starvation. _eLife_, 3:e02409. * Fritsch, Anatol

W. _et al._ Local thermodynamics govern formation and dissolution of Caenorhabditis elegans p granule condensates. _Proc. Nat. Acad. Sci._ 118(37), e2102772118 (2021). Article  CAS  Google

Scholar  * Putnam, Andrea, Cassani, Madeline, Smith, Jarrett & Seydoux, Geraldine. A gel phase promotes condensation of liquid p granules in caenorhabditis elegans embryos. _Nat. Struct.

Mol. Biol._ 26(3), 220–226 (2019). Article  CAS  Google Scholar  * Weber, Christoph A., Zwicker, David, Jülicher, Frank & Lee, Chiu Fan. Physics of active emulsions. _Rep. Prog. Phys._

82(6), 064601 (2019). Article  ADS  MathSciNet  CAS  Google Scholar  * Cahn, John W. On spinodal decomposition. _Acta Metallurgica_ 9(9), 795–801 (1961). Article  CAS  Google Scholar  *

Cahn, John W. & Hilliard, John E. Free energy of a nonuniform system. i. Interfacial free energy. _J. Chem. Phys._ 28(2), 258–267 (1958). Article  ADS  CAS  MATH  Google Scholar  * Lee,

Hyun Geun, Yang, Junxiang, Kim, Sangkwon & Kim, Junseok. Modeling and simulation of droplet evaporation using a modified cahn-hilliard equation. _Appl. Math. Comput._ 390, 125591 (2021).

MathSciNet  MATH  Google Scholar  * Zhou, Jie, Chen, Long, Huang, Yunqing & Wang, Wansheng. An efficient two-grid scheme for the cahn-hilliard equation. _Commun. Comput. Phys._ 17(1),

127–145 (2015). Article  MathSciNet  MATH  Google Scholar  * Chen, C., & Yang, X. Fully-discrete finite element numerical scheme with decoupling structure and energy stability for the

cahn-hilliard phase-field model of two-phase incompressible flow system with variable density and viscosity. _ESAIM: M2AN_, 55(5):2323–2347 (2021). * Mohammadi, Vahid & Dehghan, Mehdi.

Simulation of the phase field cahn-hilliard and tumor growth models via a numerical scheme: Element-free galerkin method. _Comput. Methods Appl. Mech. Eng._ 345, 919–950 (2019). Article  ADS

  MathSciNet  MATH  Google Scholar  * Baňas, L’ubomír & Nürnberg, Robert. Adaptive finite element methods for cahn-hilliard equations. _J. Comput. Appl. Math._ 218(1), 2–11 (2008). *

Ceniceros, Hector D. & Roma, Alexandre M. A nonstiff, adaptive mesh refinement-based method for the cahn-hilliard equation. _J. Comput. Phys._ 225(2), 1849–1862 (2007). Article  ADS 

MathSciNet  MATH  Google Scholar  * Zhang, Y., Xu, B., Weiner, B. G., Meir, Y. & Wingreen, N. S. Decoding the physical principles of two-component biomolecular phase separation. _eLife_,

10:e62403 (2021). * Schuster, Benjamin S. _et al._ Biomolecular condensates: Sequence determinants of phase separation, microstructural organization, enzymatic activity, and material

properties. _J. Phys. Chem. B_ 125(14), 3441–3451 (2021). Article  CAS  Google Scholar  * Jacobs, William M. Self-assembly of biomolecular condensates with shared components. _Phys. Rev.

Lett._ 126, 258101 (2021). Article  ADS  CAS  Google Scholar  * Zwicker, David, Hyman, Anthony A. & Jülicher, Frank. Suppression of ostwald ripening in active emulsions. _Phys. Rev. E_

92, 012317 (2015). Article  ADS  Google Scholar  * de Groot, S. R. & Masur, P. in _Non-Equilibrium Thermodynamics_. Dover Publications, (1984). * Glotzer, Sharon C., Di Marzio, Edmund A.

& Muthukumar, M. Reaction-controlled morphology of phase-separating mixtures. _Phys. Rev. Lett._ 74, 2034–2037 (1995). Article  ADS  CAS  Google Scholar  * Christensen, Jacob J., Elder,

Ken & Fogedby, Hans C. Phase segregation dynamics of a chemically reactive binary mixture. _Phys. Rev. E_ 54, R2212–R2215 (1996). Article  ADS  CAS  Google Scholar  * Lifshitz, I. M.

& Slyozov, V. V. The kinetics of precipitation from supersaturated solid solutions. _J. Phys. Chem. Solids_ 19(1), 35–50 (1961). Article  ADS  Google Scholar  * Wagner, Carl. Theorie der

alterung von niederschlägen durch umlösen (ostwald-reifung). _Zeitschrift für Elektrochemie, Berichte der Bunsengesellschaft für physikalische Chemie_ 65(7–8), 581–591 (1961). Article  CAS

  Google Scholar  * Zwicker, David. py-pde: A python package for solving partial differential equations. _J. Open Source Softw._ 5(48), 2158 (2020). Article  ADS  Google Scholar  * Caroli,

M., de Castro, P. M. M., Loriot, Sébastien, Rouiller, O., Teillaud, M. & Wormser, C. Robust and efficient delaunay triangulations of points on or close to a sphere. In Paola, F., (ed),

_Exp. Algorithms_, 462–473 (Springer Berlin Heidelberg, Berlin, Heidelberg, 2010). * Griffin, E.-E., Odde, D.-J. & Seydoux, G. Regulation of the mex-5 gradient by a spatially segregated

kinase/phosphatase cycle. _Cell_, 146(6):955–968, (2011). * Küpper, T. & Masbaum, N. Simulation of particle growth and ostwald ripening via the cahn-hilliard equation. _Acta Metallurgica

et Materialia_ 42(6), 1847–1858 (1994). Article  ADS  Google Scholar  * Vidal-Henriquez, E. & Zwicker, D. Cavitation controls droplet sizes in elastic media. _Proc. Natl. Acad. Sci._

118(40), e2102014118 (2021). Article  MathSciNet  CAS  Google Scholar  * Vidal-Henriquez, E. & Zwicker, D. Theory of droplet ripening in stiffness gradients. _Soft Matter_ 16, 5898–5905

(2020). Article  ADS  CAS  Google Scholar  * Feric, M. & Brangwynne, C. P. A nuclear f-actin scaffold stabilizes ribonucleoprotein droplets against gravity in large cells. _Nat. Cell

Biol._ 15(10), 1253–1259 (2013). Article  CAS  Google Scholar  * Böddeker, T.J. _et al._ Non-specific adhesive forces between filaments and membraneless organelles. _Nat. Phys._ 18(5),

571–578 (2022). Article  Google Scholar  * Wiegand, Tina & Hyman, Anthony A. Drops and fibers–how biomolecular condensates and cytoskeletal filaments influence each other. _Emerg. Topics

Life Sci._ 4(3), 247–261 (2020). Article  CAS  Google Scholar  * Setru, S.U. _et al._ A hydrodynamic instability drives protein droplet formation on microtubules to nucleate branches. _Nat.

Phys._ 17(4), 493–498 (2021). Article  CAS  Google Scholar  * Brangwynne, C. P., Mitchison, T. J. & Hyman, A. A. Active liquid-like behavior of nucleoli determines their size and shape

in Xenopus laevis oocytes. _Proc. Natl. Acad. Sci._ 108(11), 4334–4339 (2011). Article  ADS  CAS  Google Scholar  * Zwicker, D., Seyboldt, R., Weber, C. A., Hyman, A. A. & Jülicher, F.

Growth and division of active droplets provides a model for protocells. _Nat. Phys._ 13(4), 408–413 (2017). Article  CAS  Google Scholar  * Seyboldt, R. & Jülicher, F. Role of

hydrodynamic flows in chemically driven droplet division. _New J. Phys._ 20(10), 105010 (2018). Article  ADS  Google Scholar  * Quiroz, F. G., Fiore, V. F., Levorse, J., Polak, Lisa, Wong,

Ellen, Pasolli, H. A. & Fuchs, E. Liquid-liquid phase separation drives skin barrier formation. _Science_, 367(6483):eaax9554 (2020). * Lee, D. S., Wingreen, N. S. & Brangwynne, C.

P. Chromatin mechanics dictates subdiffusion and coarsening dynamics of embedded condensates. _Nat. Phys._ 17(4), 531–538 (2021). Article  CAS  Google Scholar  Download references

ACKNOWLEDGEMENTS The authors thank Jan Kirschbaum, Swati Sen, and Malte Thumann for helpful discussions. All authors acknowledge funding from the Max Planck Society. The authors declare that

they have no conflict of interest. FUNDING Open Access funding enabled and organized by Projekt DEAL. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Max Planck Institute for Dynamics and

Self-Organization, Am Fassberg 17, 37077, Göttingen, Germany Ajinkya Kulkarni, Estefania Vidal-Henriquez & David Zwicker Authors * Ajinkya Kulkarni View author publications You can also

search for this author inPubMed Google Scholar * Estefania Vidal-Henriquez View author publications You can also search for this author inPubMed Google Scholar * David Zwicker View author

publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS All authors designed and performed the research, analyzed data, and wrote the paper. A.K. ran the

numerical simulations and prepared the figures. CORRESPONDING AUTHOR Correspondence to David Zwicker. ADDITIONAL INFORMATION PUBLISHER'S NOTE Springer Nature remains neutral with regard

to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed

under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate

credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article

are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons

licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of

this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Kulkarni, A., Vidal-Henriquez, E. & Zwicker, D. Effective

simulations of interacting active droplets. _Sci Rep_ 13, 733 (2023). https://doi.org/10.1038/s41598-023-27630-3 Download citation * Received: 06 July 2022 * Accepted: 04 January 2023 *

Published: 13 January 2023 * DOI: https://doi.org/10.1038/s41598-023-27630-3 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link

Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative