Galvanomagnetic properties of the putative type-ii dirac semimetal ptte2

ABSTRACT Platinum ditelluride has recently been characterized, based on angle-resolved photoemission spectroscopy data and electronic band structure calculations, as a possible

representative of type-II Dirac semimetals. Here, we report on the magnetotransport behavior (electrical resistivity, Hall effect) in this compound, investigated on high-quality

single-crystalline specimens. The magnetoresistance (MR) of PtTe2 is large (over 3000% at _T_ = 1.8 K in _B_ = 9 T) and unsaturated in strong fields in the entire temperature range studied.

The MR isotherms obey a Kohler’s type scaling with the exponent _m_ = 1.69, different from the case of ideal electron-hole compensation. In applied magnetic fields, the resistivity shows a

low-temperature plateau, characteristic of topological semimetals. In strong fields, well-resolved Shubnikov – de Haas (SdH) oscillations with two principle frequencies were found, and their

analysis yielded charge mobilities of the order of 103 cm2 V−1 s−1 and rather small effective masses of charge carriers, 0.11 _m__e_ and 0.21 _m__e_. However, the extracted Berry phases

point to trivial character of the electronic bands involved in the SdH oscillations. The Hall effect data corroborated a multi-band character of the electrical conductivity in PtTe2, with

moderate charge compensation. SIMILAR CONTENT BEING VIEWED BY OTHERS TRANSPORT ANOMALIES IN THE LAYERED COMPOUND BAPT4SE6 Article Open access 23 September 2021 HETEROSTRUCTURE GROWTH,

ELECTRICAL TRANSPORT AND ELECTRONIC STRUCTURE OF CRYSTALLINE DIRAC NODAL ARC SEMIMETAL PTSN4 Article Open access 28 December 2024 HARD MAGNET TOPOLOGICAL SEMIMETALS IN _X_PT3 COMPOUNDS WITH

THE HARMONY OF BERRY CURVATURE Article Open access 21 May 2021 INTRODUCTION Topological semimetals (TSs) form an outstanding group of materials characterized by perfect linear dispersion of

some bulk electronic states1,2. In accordance with presence or absence of Lorentz invariance, one discriminates type-I and type-II systems3. In the latter class of TSs, Dirac cone is

strongly tilted with respect to Fermi level4. Both type-I and type-II TSs can be composed from Dirac or Weyl fermions, depending on what kind of symmetries is preserved5. Nontrivial

electronic structures of TSs give rise to unusual electronic transport properties, commonly considered being highly prospective for various electronic devices of new kind. A hallmark feature

of TSs is chiral magnetic anomaly (CMA), which manifests itself as a negative magnetoresistance (MR) observed when electric and magnetic fields are collinear6. Actually, negative MR was

found in many TSs, more often in type-I materials7,8,9,10,11 but also in a few type-II systems12. Another smoking-gun signature of TSs is the existence of topological surface states, which

have a form of Fermi-arcs1,2. Their presence was confirmed experimentally in a large number of TSs, among them Cd3As213, MoTe214, WTe215 and TaAs16. Type-II topological semimetallic states

have been revealed in several transition metal dichalcogenides and in MA3 (M = V, Nb, Ta; A = Al, Ga, In) icosagenides3,4,14,17,18,19,20. Within the former group of compounds, MoTe2 and WTe2

have been classified as type-II Weyl semimetals14,21, whereas platinum and palladium dichalcogenides have been established via angle-resolved photoemission spectroscopy (ARPES) experiments

to represent the family of type-II Dirac semimetals3,18,22. The TSs nature of PdTe2 is reflected in its peculiar magnetotransport behavior23,24. In turn, no comprehensive study on the

electronic transport properties of the Pt-bearing counterpart has been reported in the literature up to date. In this work, we investigated the galvanomagnetic properties of PtTe2 with the

main aim to discern features appearing due to the alleged nontrivial topology of its electronic band structure. RESULTS AND DISCUSSION ELECTRICAL RESISTIVITY, MAGNETIC FIELD-INDUCED PLATEAU

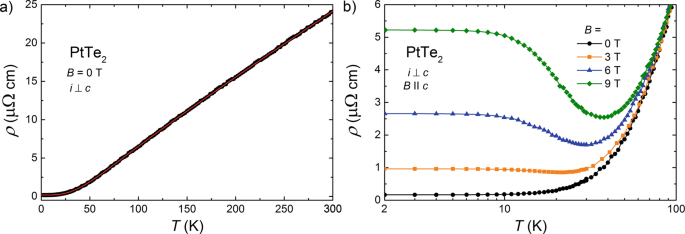
AND MAGNETORESISTANCE Figure 1a shows the results of electrical resistivity, _ρ_, measurements performed on single-crystalline sample of PtTe2, as a function of temperature, _T_, with

electric current, _i_, flowing within the hexagonal _a_ − _b_ plane. The overall behavior of _ρ_(_T_) indicates a metallic character of the compound. The resistivity decreases from the value

of 24.09 _μ_Ω cm at _T_ = 300 K to 0.17 _μ_Ω cm at _T_ = 2 K, yielding the residual resistivity ratio RRR = _ρ_(300K)/_ρ_(2K) equal to 142. The magnitudes of both _ρ_(2K) and RRR indicate

high crystallinity of the specimen measured (RRR is approximately 5 times larger than that reported for PtTe2 in ref.18). As displayed in Fig. 1a (note the red solid line), in the whole

temperature range covered, _ρ_(_T_) can be very well approximated with the Bloch-Grüneisen (BG) law: $$\rho (T)={\rho }_{0}+A{(\frac{T}{{{\Theta }}_{{\rm{D}}}})}^{k}{\int

}_{0}^{\frac{{{\Theta }}_{{\rm{D}}}}{T}}\frac{{x}^{k}}{({e}^{x}-1)(1-{e}^{-x})}dx,$$ (1) where _ρ_0 is the residual resistivity, accounting for scattering conduction electrons on crystal

imperfections, while the second term represents electron-phonon scattering (_Θ_D stands for the Debye temperature). The least-squares fitting yielded the parameters: _ρ_0 = 0.17 _μ_Ω cm,

_Θ_D = 253 K, _A_ = 11.6 _μ_Ω cm and _k_ = 3.23. The value of _k_ is smaller than _k_ = 5, expected for simple metals, yet similar to _k_ exponents determined for several

monopnictides25,26,27. The temperature dependencies of the electrical resistivity of PtTe2 measured in transverse magnetic field (_i_ ⊥ _c_ axis and \(B\,\parallel \,c\) axis) are gathered

in Fig. 1b. In non-zero _B_, _ρ_(_T_) is a non-monotonous function of temperature, showing an upturn below a certain slightly field-dependent temperature _T_*, and then forming a plateau at

the lowest temperatures. With increasing magnetic field, the magnitude of the resistivity in the turn-on and plateau regions distinctly increases. Similar behavior was considered as a

fingerprint of the presence of nontrivial topology in the electronic structure of several TSs28,29,30,31. Another possible explanation of this type of magnetic field governed changes in

_ρ_(_T_) is a metal-insulator transition29,32,33. However, as discussed first for WTe234, and afterwards, e.g., for rare-earth monopnictides25,26,27,35,36,37,38,39,40,41, the magnetic field

induced upturn in _ρ_(_T_) may appear also in trivial semimetals, which are close to perfect charge carriers compensation. We presume that the latter mechanism is also fully appropriate for

the electrical transport behavior in PtTe2. In order to examine the actual nature of the galvanomagnetic behavior observed for PtTe2, transverse magnetoresistance, MR = [_ρ_(_B_) − _ρ_(_B_ =

 0)]/_ρ_(_B_ = 0), measurements were performed at several constant temperatures in the configuration _i_ ⊥ _c_ axis and \(B\,\parallel \,c\) axis. As can be inferred from Fig. 2a, in _B_ = 9

 T, MR taken at _T_ = 1.8 K achieves a giant value of 3060%, which is an order of magnitude larger than MR determined in the same conditions for the related system PdTe223, and almost equal

to that reported for the type-II Weyl semimetal MoTe242. With increasing temperature, MR measured in _B_ = 9 T does not change significantly up to about 10 K (i.e., in the plateau region of

_ρ_(_T_)), and then decreases rapidly. However, even at _T_ = 150 K, MR remains exceptionally large exceeding 500% in 9 T. At each of the temperatures studied, MR shows no tendency towards

saturation in strong fields. MR behavior similar to that of PtTe2 was established before for several TSs23,28,30,42,43,44. However, unsaturated MR can be also attributed to perfect or almost

perfect carrier compensation in a semimetallic material45. Remarkably, as demonstrated in Fig. 2b, the MR isotherms of PtTe2 obey the Kohler’s rule in the entire temperature range studied.

This finding rules out the scenario of metal-insulator transition as a possible mechanism of the magnetic field driven changes in the electrical transport of PtTe2. The MR data collapse onto

a single curve, which can be approximated by the expression: MR ∝ (_B_/_ρ_0)_m_, with the exponent _m_ = 1.69 (note the red solid line in Fig. 2b). While _m_ = 2 is expected for materials

with perfect electron-hole balance, and the obtained value is also smaller than _m_ = 1.92 reported for WTe234, it is similar to those found for some monopnictides, which were reported as

trivial semimetals fairly close to charge compensation26,37,40. QUANTUM OSCILLATIONS In order to characterize the Fermi surface in PtTe2, we investigated quantum oscillations in _ρ_(_B_)

(Shubnikov–de Haas effect) at a few different temperatures. Figure 3a shows the oscillatory part of the electrical resistivity, Δ_ρ_, obtained by subtraction of the second-order polynomial

from the experimental data, plotted as a function of reciprocal magnetic field, 1/_B_. As can be inferred from this figure, the SdH oscillations remain discernible at temperatures up to at

least 15 K, however, their amplitudes systematically decrease with increasing temperature. Fast Fourier transform (FFT) analysis, the results of which are presented in Fig. 3b, disclose four

features at the oscillations frequencies \({f}_{i}^{{\rm{FFT}}}\) (_i_ represents the Fermi surface pocket label). The most prominent peak occurs at \({f}_{\alpha

}^{{\rm{FFT}}}=108\,{\rm{T}}\), and the corresponding Fermi surface pocket will be labeled thereinafter as _α_. The next feature occurs at \({f}_{2\alpha }^{{\rm{FFT}}}=215\,{\rm{T}}\) and

it is the second harmonic frequency of \({f}_{\alpha }^{{\rm{FFT}}}\). Then, the peak with its maximum at \({f}_{\beta }^{{\rm{FFT}}}=246\,{\rm{T}}\) can be attributed to another Fermi

surface pocket, labeled _β_ in what follows. Eventually, the very weak maximum centered at \({f}_{3\alpha }^{{\rm{FFT}}}=325\,{\rm{T}}\) likely arises as the third harmonics of \({f}_{\alpha

}^{{\rm{FFT}}}\). It is worthwhile noting that the FFT spectrum of PtTe2 is very similar to that reported for PdTe2 in ref.23 but differs from the FFT data shown for the same compound in

ref.24. Using the Onsager relation \({f}_{i}^{{\rm{FFT}}}=hS/e\), where _S_ stands for the area of Fermi surface cross-section, one finds for the two pockets in PtTe2 the values _S__α_ = 

1.03 × 10−2 Å−2 and _S__β_ = 2.34×10−2 Å−2. Assuming circular cross-sections, the corresponding Fermi wave vectors are _k_F,_α_ = 5.73 ×10 −2 Å−1 and _k_F,_β_ = 8.63 × 10−2 Å−1. Then, if we

assume that both Fermi surface pockets are spherical, which is poor approximation, the carrier densities in these two pockets would be equal to _n__α_ = 6.35 × 1018 cm−3 and _n__β_ = 2.17 × 

1019 cm−3. The electronic structure calculated for PtTe23,18 comprises three bands crossing the Fermi level, one hole-like band, located at the center of the Brillouin zone, and two

electron-like bands. The fact that we observed experimentally only two principle frequencies is probably due to very small size of the third Fermi surface pocket or might arise owing to

somewhat lower position of the Fermi level in the single crystal studied. From the comparison of the values of _k_F,_i_ obtained from the FFT analysis and sizes of the calculated electronic

bands3, one may presume that the _α_ Fermi surface pocket corresponds to one of the electron-like bands and the _β_ Fermi surface pocket represents the hole-like band. The inset to Fig. 3b

displays the temperature variations of the FFT amplitudes, _R__i_(_T_), corresponding to the _α_ and _β_ Fermi surface pockets in PtTe2. The gradual damping of both oscillations with rising

temperature can be described by formula46: $${R}_{i}(T)\propto (\lambda {m}_{i}^{\ast }T/{B}_{{\rm{eff}}})/\sinh (\lambda {m}_{i}^{\ast }T/{B}_{{\rm{eff}}}),$$ (2) where \({m}_{i}^{\ast }\)

is the effective cyclotron mass of charge carriers, _B_eff = 4.5 T was calculated as _B_eff = 2/(1/_B_1 + 1/_B_2) (_B_1 = 3 T and _B_2 = 9 T are the borders of the magnetic field window in

which the FFT analysis was performed), and _λ_ = 14.7 T/K was obtained from the relationship _λ_ = 2_π_2_k_B_m_e/_eħ_ (_m_e stands for the free electron mass, and _k_B is the Boltzmann

constant). The fitting shown in the inset to Fig. 3b yielded \({m}_{\alpha }^{\ast }=0.11{m}_{e}\) and \({m}_{\beta }^{\ast }=0.21{m}_{e}\). It is worth noting that the effective mass

determined for the _α_ Fermi surface pocket in PtTe 2 is almost equal to that reported for the Pd-bearing counterpart23. In the next step, we attempted to determine the phase shift, _φ__i_,

in the SdH oscillations, which is directly related to the Berry phase, _φ_B,_i_, of the carries involved. There are known a few methods of extracting _φ__i_, and the proper interpretation of

their values remains debatable47,48,49,50. The most reliable approach is direct fitting to the experimental data of the Lifshitz-Kosevich (LK) function46: $${\rm{\Delta }}\rho \propto

\frac{1}{\sqrt{B}}\sum _{i}\frac{{p}_{i}\lambda {m}_{i}^{\ast }T/B}{\sinh ({p}_{i}\lambda {m}_{i}^{\ast }T/B)}\exp (\,-\,{p}_{i}\lambda {m}_{i}^{\ast }{T}_{D,i}/B)\cos \,\mathrm{(2}\pi

({p}_{i}{f}_{i}/B+{{\phi }}_{i})),$$ (3) where _p__i_ is the harmonic number, _f__i_ is the oscillation frequency, and _T_D,i stands for the Dingle temperature. In Fig. 4a, there is shown

the result of fitting the LK function to the oscillating resistivity of PtTe2 observed at _T_ = 1.8 K (note the red solid line). As discussed above, at this temperature, the FFT spectrum

comprises three peaks, and thus the sum in Eq. 3 consists of as many as three contributions. In order to reduce the total number of free parameters in this equation, the effective masses

were fixed at the values obtained from Eq. 2 (see above). With this simplification, one obtained the parameters: _f__α_ = 108.1 T, _T_D,_α_ = 9.1 K and _φ__α_ = 0.65 for the _α_ band, and

_f__β_ = 246 T, _T_D,_β_ = 5 K and _φ__β_ = 0.54 for the _β_ band. Remarkably, the so-obtained values of _f__i_ are almost identical to those derived from the afore-described FFT analysis,

hence confirming the internal consistency of the approach applied. Using the Dingle temperatures, the quantum relaxation time, _τ__q_,_i_, could be calculated from the relation _τ__q_,_i_ = 

_ħ_/(2_πk_B_T_D,_i_) to be equal to 1.34 × 10−13 s and 2.43 × 10−13 s for the _α_ and _β_ bands, respectively. Then, the quantum mobility of charge carriers, _μ__q_,_i_, were estimated from

the relationship \({\mu }_{q,i}=e{\tau }_{q,i}/{m}_{i}^{\ast }\) to be 2138 cm2 V−1 s−1 and 2038 cm2 V−1 s−1 for the _α_ and _β_ bands, respectively. The phase shift _φ__i_ in Eq. 3 is

generally a sum _φ__i_ = −1/2 + _φ__B_,_i_ + _δ__i_, where _δ__i_ represents the dimension-dependent correction to the phase shift49. In two-dimensional (2D) case, this parameter amounts

zero, while in three-dimensional (3D) case _δ__i_ is equal to ±1/8, and its sign depends on type of charge carriers and kind of cross-section extremum. Supposing that the SdH oscillations in

PtTe 2 originate from 3D bands with carriers moving on their maximal orbits, one can set _δ_ = −1/8 for electrons and _δ_ = 1/8 for holes. With this assumption, the Berry phases _φ__B_,_α_ 

= 0.55_π_ and _φ__B_,_β_ = 1.83_π_ were obtained for the _α_ and _β_ bands, respectively. To check the reliability of the LK analysis performed, Eq. 3 was also used to describe the

experimental data measured at _T_ = 10 K. At this temperature, just one peak in the FFT spectrum is discernible (see Fig. 3b), which corresponds to the _α_ Fermi surface pocket. The result

of fitting the LK formula is presented in Fig. 4b (note the red solid line), and the so-derived values of the parameters are: _f__α_ = 108.1 T, _T_D,_α_ = 12.6 K and _φ__B_,_α_ = 0.46_π_.

Notably, the agreement between the _f__α_ values obtained at _T_ = 10 K and _T_ = 1.8 K is perfect. The value of _T_D,_α_ implies _μ__q_ = 1544 cm2 V−1 s−1. Clearly, with increasing

temperature, the Dingle temperature increases and consequently the quantum charge carriers mobility becomes smaller, which is probably due to increasing the scattering rate. In turn, the

Berry phase of the _α_ band was found almost independent of temperature. All the parameters obtained from the LK approach to the magnetotransport in PtTe 2 are gathered in Table 1. Another

commonly applied technique for Berry phase derivation is using Landau level (LL) fan diagrams. Though in case of multi-frequency oscillations this method is obstructed by possible

superposition of the quantum oscillation peaks that hinders precise determination of the Landau level index for a given frequency51, we made an attempt to construct the LL fan diagram for

the _α_ Fermi pocket in PtTe2. As it is apparent from Fig. 3b, the FFT maximum occurring at \({f}_{\alpha }^{FFT}=108\,{\rm{T}}\) is fairly well separated from the other FFT peaks, and hence

one could filter this oscillation with reasonably high accuracy. For PtTe2 one finds \(\rho > {\rho }_{xy}\) (_ρ__xy_ is the Hall resistivity discussed in the next section), and

therefore the maxima in the oscillatory resistivity measured at _T_ = 1.8 K (see Fig. 4a) were numbered by integers, _n_, and the minima by half-integers, _n_ + 1/2. The result of this

approach is shown in the main panel of Fig. 5. A linear fit of the LL indices (note the solid line) gives an intercept of 0.62, which corresponds to the Berry phase _φ__B_,_α_ = 0.51_π_. In

turn, the slope of this straight line defines the oscillation frequency _f__α_ = 108.3 T. At _T_ = 10 K, the electrical resistivity of PtTe2 oscillates in the transverse magnetic field with

only one frequency (cf. Fig. 3b), so building the LL fan diagram is straightforward. As can be inferred from the inset to Fig. 5, the LL indices plot yields the intercept 0.63, which is

almost the same as that obtained at the lower temperature. Also, the slope of the straight line (_f__α_ = 108.3 T) is identical with that determined at 1.8 K, and furthermore it is very

close to the FFT value (see Table 1). Most importantly, all the parameters extracted from the LL indices plots are in perfect agreement with the quantities obtained for the _α_ Fermi pocket

from the LK analysis, which unambiguously corroborates the correctness of both techniques applied for PtTe2. HALL EFFECT The results of Hall resistivity measurements, performed on

single-crystalline PtTe2 with electric current flowing within the basal plane of the hexagonal unit cell and magnetic field applied along the _c_ axis, are shown in Fig. 6a. At _T_ = 2 K,

_ρ__xy_(_B_) behaves in a rather complex manner. In weak magnetic fields, it is negative and exhibits a shallow minimum. Near 2 T, the Hall resistivity changes sign to positive, and then its

magnitude increases with increasing _B_. The _ρ__xy_(_B_) isotherm measured at 25 K shows a fairly similar field variation, yet the positive contribution in strong fields remains too small

to cause sign reversal. At higher temperatures, one observes a gradual straightening of the _ρ__xy_(_B_) with rising _T_. The overall behavior of the Hall effect in PtTe2 confirms the

multi-band character of the electrical transport in this material. It is worth recalling that very similar Hall response was observed for the closely related compound PdTe224. For

quantitative analysis of the experimental data, first a two-bands Drude model was applied. For this purpose, _ρ__xy_(_B_) measured at _T_ = 2 K was converted to the Hall conductivity

\({\sigma }_{xy}={\rho }_{xy}/({\rho }_{xy}^{2}+{\rho }^{2})\), as displayed in Fig. 6b. Next, _σ__xy_(_B_) was fitted by the formula: $${\sigma }_{xy}(B)=eB(\frac{{n}_{h}{\mu

}_{h}^{2}}{1+{({\mu }_{h}B)}^{2}}+\frac{{n}_{e1}{\mu }_{e1}^{2}}{1+{({\mu }_{e1}B)}^{2}}),$$ (4) where _n__e_1 and _μ__e_1, _n__h_ and _μ__h_ stand for the carrier concentrations and the

carrier mobilities of electron- and hole-like bands, respectively. As can be inferred from Fig. 6b, the so-obtained approximation of the measured _σ__xy_(_B_) data (note the blue dashed

line) is not ideal. An obvious reason for the discrepancy between the experiment and the two-band model could be contribution from another band, the presence of which was revealed in the

ab-initio calculations of the electronic structure of PtTe23,18. Therefore, in the next step, the Hall conductivity was analysed in terms of a three-bands model: $${\sigma

}_{xy}(B)=eB(\frac{{n}_{h}{\mu }_{h}^{2}}{1+{({\mu }_{h}B)}^{2}}+\frac{{n}_{e1}{\mu }_{e1}^{2}}{1+{({\mu }_{e1}B)}^{2}}+\frac{{n}_{e2}{\mu }_{e2}^{2}}{1+{({\mu }_{e2}B)}^{2}})\mathrm{.}$$

(5) where _n__e_2 and _μ__e_2 account for the carrier concentration and the carrier mobility, respectively, of another electron-like band in PtBi2. The result of fitting Eq. 5 to the

experimental _σ__xy_(_B_) data is shown as red solid line in Fig. 6b. Clearly, the obtained description is much better than that with the two-bands model. The fitting parameters derived in

the two approaches are listed in Table 2. Both models yielded large carriers concentrations of the order of 1020 cm−3. It is worth noting that very similar charge densities were found in the

Dirac semimetal PtBi252. On the contrary, for the type-II Weyl semimetal WTe2 the carrier concentrations were reported to be up to two orders of magnitude larger than those in PtTe253. As

regards the level of carrier compensation, the two-bands model yielded considerable charge imbalance given by the ratio _n__h_/_n__e_1 = 1.19, however the three-bands model led to fairly

balanced scenario _n__h_/(_n__e_1 + _n__e_2) = 1.04. Recently, similar degree of electron-hole compensation was established, e.g., in semimetallic monobismuthides YBi and LuBi27. The

mobilities of charge carriers in PtTe 2 were found very high, especially that obtained for one of the electron-like Fermi surface pockets (\({\mu }_{e1}\sim 2\times

{10}^{4}\,\,{{\rm{c}}{\rm{m}}}^{2}{{\rm{V}}}^{-1}{{\rm{s}}}^{-1}\)). Though the latter value is not such large as the carriers mobilities in Cd3As254 or NbP28 it exceeds the values reported

for type-II Weyl semimetals MoTe242, WTe255, and WP253. It is worth noting that the carriers mobility derived from the Hall effect data are larger than the quantum mobilities determined in

the analyses of the SdH oscillations. Similar finding was reported for other TSs, like Cd3As254, ZrSiS56, WP243, and PtBi252. The discrepancy likely arises due to the fact that the quantum

mobility is affected by all possible scattering processes, whereas the Hall mobility is sensitive to small-angle scattering only46. ANGLE-DEPENDENT MAGNETORESISTANCE In order to check

whether PtTe2 demonstrates CMA, angle-dependent magnetotransport measurements were performed at _T_ = 2 K. In these experiments, electric current was always flowing within the hexagonal _a_ 

− _b_ plane, while the angle _θ_ between current and magnetic field direction was varied from _θ_ = 90° (_B_ ⊥ _i_) to _θ_ = 0° (\(B\,\parallel \,i\)). As can be inferred from Fig. 7, the

electrical resistivity rapidly decreases on deviating from the transverse configuration, and eventually for the longitudinal geometry _ρ_ measured in _B_ = 9 T is about an order of magnitude

smaller than that for _B_ ⊥ _i_. Clearly, the longitudinal MR experiments did not provide any evidence for CMA in PtTe2. A possible source for that may be large contribution of non-Dirac

states to the measured resistivity. At odds with the Drude theory, which predicts zero MR for \(B\,\parallel \,i\)57, in several materials sizeable positive longitudinal MR was observed.

Among the theories which interpret this phenomenon58,59,60,61, that accounting for Fermi surface anisotropy61 seems appropriate for PtTe2. Within the latter approach, positive longitudinal

MR up to \(\sim \mathrm{100 \% }\) can be expected for strongly anisotropic systems. In consequence, CMA would be discernible only if its negative contribution to the longitudinal MR is

larger than the positive term due to trivial electronic bands. CONCLUSIONS Our comprehensive investigations of the galvanomagnetic properties of the alleged type-II Dirac semimetal PtTe2,

performed on high-quality single crystals, have not provided any definitive proof of the the presence of Dirac states in this material. The conclusion was hampered by the existence of

trivial bands at the Fermi level, which significantly contribute to the electrical transport. In particular, CMA effect was not resolved, and transverse MR was found to obey the Kohler’s

scaling. From the analysis of the Hall effect and the SdH oscillations, very high mobilities of charge carriers with small effective masses were extracted. However, the derived Berry phases,

different from the value of _π_ expected for Dirac fermions, indicate that the SdH effect is governed predominantly by trivial electronic states. This finding is in concert with the

electronic band structure calculations, which showed that the Dirac point in PtTe2 is located below the Fermi level3. Further investigations performed on suitably doped or pressurized

material might result in observation of clear contribution of Dirac states to its transport properties, caused by appropriate tuning the chemical potential. Based on the hitherto obtained

results, PtTe2 can be classified as a semimetal with moderate degree of the charge carriers compensation. METHODS Single crystals of PtTe2 were grown by flux method. High-purity constituents

(Pt 5 N, Te 6 N), taken in atomic ratio 1:20, were placed in an alumina crucible covered by molybdenum foil strainer and capped with another inverted alumina crucible. This set was sealed

inside a quartz tube under partial Ar gas atmosphere. The ampoule tube was heated up to 1150 °C, held at this temperature for 24 hours, then quickly cooled down to 850 °C at a rate of 50 

°C/h, kept at this temperature for 360 hours, followed by slow cooling down to 550 °C at a rate of 5 °C/h. Subsequently, the tube was quenched in cold water. Upon flux removal by

centrifugation, multitude of single crystals with typical dimensions 3 × 2 × 0.4 mm3 were isolated. Their had metallic luster and were found stable against air and moisture. Chemical

composition of the single crystals obtained was checked by energy-dispersive X-ray analysis using a FEI scanning electron microscope equipped with an EDAX Genesis XM4 spectrometer. The

average elemental ratio Pt: Te = 35.2(5): 64.8(3) was derived, in accord with the expected stoichiometry. The crystal structure of the single crystals was examined by X-ray diffraction on a

KUMA Diffraction KM-4 four-circle diffractometer equipped with a CCD camera, using graphite-monochromatized Cu-K_α_1 radiation. The hexagonal CdI2-type crystal structure (space group

\(P\overline{3}m1\), Wyckoff No. 164) reported in ref.62 was confirmed, with the lattice parameters very close to the literature values. Crystallinity and orientation of the crystal used in

the electrical transport studies was checked by Laue backscattering technique employing a Proto LAUE-COS system. Due to the layered crystal structure of PtTe2 it was possible to obtain very

thin samples by scotch-tape technique with their surface corresponding to the _a_ − _b_ plane of the hexagonal unit cell of the compound. Rectangular-shaped specimen with dimensions 2.9 × 

1.3 × 0.04 mm3 was cut from the cleaved single crystal using a scalpel. Electrical contacts were made from 50 μm thick silver wires attached to the sample using silver epoxy paste.

Electrical transport measurements were carried out within the temperature range 2–300 K and in magnetic field up to 9 μT using a conventional four-point ac technique implemented in a Quantum

Design PPMS platform. DATA AVAILABILITY The datasets analysed during the current study are available from the corresponding author on reasonable request. REFERENCES * Hasan, M. Z., Xu,

S.-Y., Belopolski, I. & Huang, S.-M. Discovery of Weyl fermion semimetals and topological Fermi arc states. _Ann. Rev. Cond. Mat. Phys._ 8, 289–309 (2017). Article  ADS  CAS  Google

Scholar  * Armitage, N. P., Mele, E. J. & Vishwanath, A. Weyl and Dirac semimetals in three dimensional solids. _Rev. Mod. Phys._ 90, 015001 (2017). Article  ADS  MathSciNet  Google

Scholar  * Yan, M. _et al_. Lorentz-violating type-II Dirac fermions in transition metal dichalcogenide PtTe2. _Nat. Commun._ 8, 257 (2017). Article  ADS  PubMed  PubMed Central  CAS  Google

Scholar  * Soluyanov, A. A. _et al_. Type-II Weyl semimetals. _Nature_ 527, 495–498 (2015). Article  ADS  PubMed  CAS  Google Scholar  * Yang, B.-J. & Nagaosa, N. Classification of

stable three-dimensional Dirac semimetals with nontrivial topology. _Nat. Commun._ 5, 4898 (2014). Article  PubMed  CAS  Google Scholar  * Nielsen, H. B. & Ninomiya, M. The

Adler-Bell-Jackiw anomaly and Weyl fermions in a crystal. _Phys. Lett. B_ 130, 389–396 (1983). Article  ADS  MathSciNet  Google Scholar  * Li, C. Z. _et al_. Giant negative magnetoresistance

induced by the chiral anomaly in individual Cd3As2 nanowires. _Nature Commun._ 6, 10137 (2015). Article  ADS  PubMed  PubMed Central  CAS  Google Scholar  * Li, Q. _et al_. Chiral magnetic

effect in ZrTe5. _Nat. Phys._ 12, 550 (2016). Article  ADS  CAS  Google Scholar  * Hirschberger, M. _et al_. The chiral anomaly and thermopower of Weyl fermions in the half-Heusler GdPtBi.

_Nat. Mater._ 15, 1161 (2016). Article  ADS  PubMed  CAS  Google Scholar  * Niemann, A. C. _et al_. Chiral magnetoresistance in the Weyl semimetal NbP. _Sci. Rep._ 7, 43394 (2017). Article 

ADS  PubMed  PubMed Central  Google Scholar  * Xiong, J. _et al_. Evidence for the chiral anomaly in the Dirac semimetal Na3Bi. _Science_ 350, 413 (2015). Article  ADS  MathSciNet  PubMed 

MATH  CAS  Google Scholar  * Lv, Y.-Y. _et al_. Experimental observation of anisotropic Adler-Bell-Jackiw anomaly in type-II Weyl semimetal WTe1.98 crystals at the quasiclassical regime.

_Phys. Rev. Lett._ 118, 096603 (2017). Article  ADS  PubMed  Google Scholar  * Wang, L.-X., Li, C.-Z., Yu, D.-P. & Liao, Z.-M. Aharonov–Bohm oscillations in Dirac semimetal Cd3As2

nanowires. _Nat. Commun._ 7, 10769 (2016). Article  ADS  PubMed  PubMed Central  CAS  Google Scholar  * Deng, K. _et al_. Experimental observation of topological Fermi arcs in type-II Weyl

semimetal MoTe2. _Nat. Phys._ 12, 1105–1110 (2016). Article  CAS  Google Scholar  * Li, P. _et al_. Evidence for topological type-II Weyl semimetal WTe2. _Nat. Commun._ 8, 2150 (2017).

Article  ADS  PubMed  PubMed Central  CAS  Google Scholar  * Lv, B. Q. _et al_. Experimental discovery of weyl semimetal TaAs. _Phys. Rev. X_ 5, 031013 (2015). Article  ADS  CAS  Google

Scholar  * Chang, T.-R. _et al_. Type-II symmetry-protected topological Dirac semimetals. _Phys. Rev. Lett._ 119, 026404 (2017). Article  ADS  PubMed  Google Scholar  * Zhang, K. _et al_.

Experimental evidence for type-II Dirac semimetal in PtSe2. _Phys. Rev. B_ 96, 125102 (2017). Article  ADS  Google Scholar  * Autès, G., Gresch, D., Troyer, M., Soluyanov, A. A. &

Yazyev, O. V. Robust type-II Weyl semimetal phase in transition metal diphosphides _X_P (_X_ = Mo, W). _Phys. Rev. Lett._ 117, 066402 (2016). Article  ADS  PubMed  CAS  Google Scholar  *

Huang, H., Zhou, S. & Duan, W. Type-II Dirac fermions in the PtSe2 class of transition metal dichalcogenides. _Phys. Rev. B_ 94, 121117 (2016). Article  ADS  Google Scholar  * Bruno, F.

Y. _et al_. Observation of large topologically trivial Fermi arcs in the candidate type-II Weyl semimetal WTe2. _Phys. Rev. B_ 94, 121112 (2016). Article  ADS  Google Scholar  * Noh, H.-J.

_et al_. Experimental realization of type-II Dirac fermions in a PdTe2 Superconductor. _Phys. Rev. Lett._ 119, 016401 (2017). Article  ADS  PubMed  Google Scholar  * Wang, Y. _et al_. De

Hass-van Alphen and magnetoresistance reveal predominantly single-band transport behavior in PdTe2. _Sci. Rep._ 6, 31554 (2016). Article  ADS  PubMed  PubMed Central  CAS  Google Scholar  *

Fei, F. _et al_. Nontrivial Berry phase and type-II Dirac transport in the layered material PdTe2. _Phys. Rev. B_ 96, 041201 (2017). Article  ADS  Google Scholar  * Sun, S., Wang, Q., Guo,

P.-J., Liu, K. & Lei, H. Large magnetoresistance in LaBi: Origin of field-induced resistivity upturn and plateau in compensated semimetals. _New J. Phys._ 18, 082002 (2016). Article  ADS

  CAS  Google Scholar  * Pavlosiuk, O., Kleinert, M., Swatek, P., Kaczorowski, D. & Wiśniewski, P. Fermi surface topology and magnetotransport in semimetallic LuSb. _Sci. Rep._ 7, 12822

(2017). Article  ADS  PubMed  PubMed Central  CAS  Google Scholar  * Pavlosiuk, O., Swatek, P., Kaczorowski, D. & Wiśniewski, P. Magnetoresistance in LuBi and YBi semimetals due to

nearly perfect carrier compensation. _Phys. Rev. B_ 97, 235132 (2018). Article  ADS  Google Scholar  * Shekhar, C. _et al_. Extremely large magnetoresistance and ultrahigh mobility in the

topological Weyl semimetal candidate NbP_. Nat. Phys._ 11, 645 (2015). Article  CAS  Google Scholar  * Li, Y. _et al_. Resistivity plateau and negative magnetoresistance in the topological

semimetal TaSb2. _Phys. Rev. B_ 94, 121115 (2016). Article  ADS  Google Scholar  * Singha, R., Pariari, A. K., Satpati, B. & Mandal, P. Large nonsaturating magnetoresistance and

signature of nondegenerate Dirac nodes in ZrSiS. _Proc. Natl. Acad. Sci._ 114, 2468 (2017). Article  PubMed  CAS  Google Scholar  * Hosen, M. M. _et al_. Tunability of the topological

nodal-line semimetal phase in ZrSi_X_-type materials (_X_ = S, Se, Te). _Phys. Rev. B_ 95, 161101 (2017). Article  ADS  Google Scholar  * Zhao, Y. _et al_. Anisotropic magnetotransport and

exotic longitudinal linear magnetoresistance in WTe2 crystals. _Phys. Rev. B_ 92, 041104 (2015). Article  ADS  CAS  Google Scholar  * Du, X., Tsai, S.-W., Maslov, D. L. & Hebard, A. F.

Metal-insulator-like behavior in semimetallic bismuth and graphite. _Phys. Rev. Lett._ 94, 166601 (2005). Article  ADS  PubMed  CAS  Google Scholar  * Wang, Y. L. _et al_. Origin of the

turn-on temperature behavior in WTe2. _Phys. Rev. B_ 92, 180402 (2015). Article  ADS  CAS  Google Scholar  * Zeng, L.-K. _et al_. Compensated semimetal LaSb with unsaturated

magnetoresistance. _Phys. Rev. Lett._ 117, 127204 (2016). Article  ADS  PubMed  CAS  Google Scholar  * Niu, X. H. _et al_. Presence of exotic electronic surface states in LaBi and LaSb.

_Phys. Rev. B_ 94, 165163 (2016). Article  ADS  CAS  Google Scholar  * Pavlosiuk, O., Swatek, P. & Wiśniewski, P. Giant magnetoresistance, three-dimensional Fermi surface and origin of

resistivity plateau in YSb semimetal. _Sci. Rep._ 6, 38691 (2016). Article  ADS  PubMed  PubMed Central  CAS  Google Scholar  * Kumar, N. _et al_. Observation of pseudo-two-dimensional

electron transport in the rock salt-type topological semimetal LaBi. _Phys. Rev. B_ 93, 241106 (2016). Article  ADS  Google Scholar  * Ghimire, N. J., Botana, A. S., Phelan, D., Zheng, H.

& Mitchell, J. F. Magnetotransport of single crystalline YSb. _J. Phys. Condens. Matter_ 28, 235601 (2016). Article  ADS  PubMed  CAS  Google Scholar  * Han, F. _et al_. Separation of

electron and hole dynamics in the semimetal LaSb. _Phys. Rev. B_ 96, 125112 (2017). Article  ADS  Google Scholar  * Xu, J. _et al_. Origin of the extremely large magnetoresistance in the

semimetal YSb. _Phys. Rev. B_ 96, 075159 (2017). Article  ADS  Google Scholar  * Chen, F. C. _et al_. Extremely large magnetoresistance in the type-II Weyl semimetal MoTe2. _Phys. Rev. B_

94, 235154 (2016). Article  ADS  Google Scholar  * Kumar, N. _et al_. Extremely high magnetoresistance and conductivity in the type-II Weyl semimetals WP2 and MoP2. _Nat. Commun._ 8, 1642

(2017). Article  ADS  PubMed  PubMed Central  CAS  Google Scholar  * Wang, X. _et al_. Evidence of both surface and bulk Dirac bands and anisotropic nonsaturating magnetoresistance in ZrSiS.

_Adv. Electr. Mater._ 2, 1600228 (2016). Article  CAS  Google Scholar  * Ziman, J. _Principles of the Theory of Solids_ (Cambridge University Press, 1972). * Shoenberg, D. _Magnetic

Oscillations in Metals_ (Cambridge University Press, 1984). * Ando, Y. Topological insulator materials. _J. Phys. Soc. Jpn._ 82, 102001 (2013). Article  ADS  CAS  Google Scholar  * Wang, C.

M., Lu, H. Z. & Shen, S. Q. Anomalous phase shift of quantum oscillations in 3D topological semimetals. _Phys. Rev. Lett._ 117, 077201 (2016). Article  ADS  PubMed  CAS  Google Scholar 

* Li, C. _et al_. Rules for phase shifts of quantum oscillations in topological nodal-line semimetals. _Phys. Rev. Lett._ 120, 146602 (2018). Article  ADS  PubMed  Google Scholar  * Taskin,

A. A. & Ando, Y. Berry phase of nonideal Dirac fermions in topological insulators. _Phys. Rev. B_ 84, 035301 (2011). Article  ADS  CAS  Google Scholar  * Hu, J. _et al_. _π_ Berry phase

and Zeeman splitting of Weyl semimetal TaP. _Sci. Rep._ 6, 18674 (2016). Article  ADS  PubMed  PubMed Central  CAS  Google Scholar  * Gao, W. _et al_. Extremely large magnetoresistance in a

topological semimetal candidate pyrite PtBi2. _Phys. Rev. Lett._ 118, 256601 (2017). Article  ADS  PubMed  Google Scholar  * Wang, A. _et al_. Large magnetoresistance in the type-II Weyl

semimetal WP2. _Phys. Rev. B_ 96, 121107 (2017). Article  ADS  Google Scholar  * Liang, T. _et al_. Ultrahigh mobility and giant magnetoresistance in the Dirac semimetal Cd3As2. _Nat.

Mater._ 14, 280–284 (2015). Article  ADS  PubMed  CAS  Google Scholar  * Luo, Y. _et al_. Hall effect in the extremely large magnetoresistance semimetal WTe2. _Appl. Phys. Lett._ 107, 182411

(2015). Article  ADS  CAS  Google Scholar  * Hu, J. _et al_. Nearly massless Dirac fermions and strong Zeeman splitting in the nodal-line semimetal ZrSiS probed by de Haas - van Alphen

quantum oscillations. _Phys. Rev. B_ 96, 045127 (2017). Article  ADS  Google Scholar  * Pippard, A. _Magnetoresistance in Metals_ (Cambridge University Press, 2009). * Miller, D. &

Laikhtman, B. Longitudinal magnetoresistance of superlattices caused by barrier inhomogeneity. _Phys. Rev. B_ 54, 10669 (1996). Article  ADS  CAS  Google Scholar  * Argyres, P. N. &

Adams, E. N. Longitudinal magnetoresistance in the quantum limit. _Phys. Rev._ 104, 900 (1956). Article  ADS  MATH  Google Scholar  * Stroud, D. & Pan, F. P. Effect of isolated

inhomogeneities on the galvanomagnetic properties of solids. _Phys. Rev. B_ 13, 1434 (1976). Article  ADS  CAS  Google Scholar  * Pal, H. K. & Maslov, D. L. Necessary and sufficient

condition for longitudinal magnetoresistance. _Phys. Rev. B_ 81, 214438 (2010). Article  ADS  CAS  Google Scholar  * Faruseth, S., Selte, K. & Kjekshus, A. Redetermined crystal

structures of NiTe2, PdTe2, PtS2, PtSe2 and PtTe2. _Acta Chem. Scand._ 19, 257 (1965). Article  Google Scholar  Download references AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Institute of

Low Temperature and Structure Research, Polish Academy of Sciences, P. O. Box 1410, 50-950 Wrocław, Poland Orest Pavlosiuk * Institute of Molecular Physics, Polish Academy of Sciences,

Mariana Smoluchowskiego 17, 60-179, Poznań, Poland Dariusz Kaczorowski Authors * Orest Pavlosiuk View author publications You can also search for this author inPubMed Google Scholar *

Dariusz Kaczorowski View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS D.K. conceived the experiments and performed preliminary electrical

transport studies. O.P. conducted the experiments and analysed the data. Both authors contributed to discussion of the results and writing the manuscript. CORRESPONDING AUTHOR Correspondence

to Dariusz Kaczorowski. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER'S NOTE: Springer Nature remains neutral

with regard to jurisdictional claims in published maps and institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0

International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the

source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative

Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by

statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit

http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Pavlosiuk, O., Kaczorowski, D. Galvanomagnetic properties of the putative type-II

Dirac semimetal PtTe2. _Sci Rep_ 8, 11297 (2018). https://doi.org/10.1038/s41598-018-29545-w Download citation * Received: 23 May 2018 * Accepted: 09 July 2018 * Published: 26 July 2018 *

DOI: https://doi.org/10.1038/s41598-018-29545-w SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is

not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative