Efficient coding of cognitive variables underlies dopamine response and choice behavior

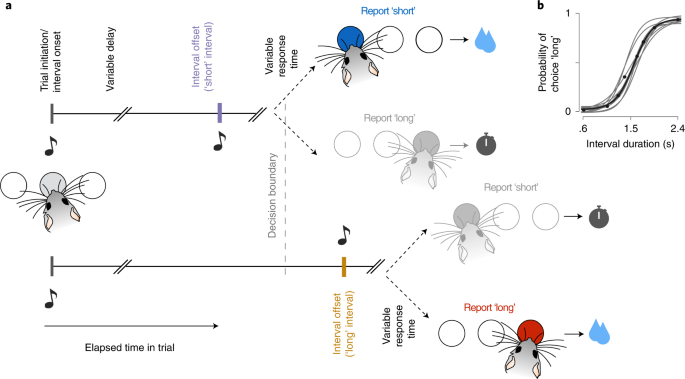
ABSTRACT Reward expectations based on internal knowledge of the external environment are a core component of adaptive behavior. However, internal knowledge may be inaccurate or incomplete

due to errors in sensory measurements. Some features of the environment may also be encoded inaccurately to minimize representational costs associated with their processing. In this study,

we investigated how reward expectations are affected by features of internal representations by studying behavior and dopaminergic activity while mice make time-based decisions. We show that

several possible representations allow a reinforcement learning agent to model animals’ overall performance during the task. However, only a small subset of highly compressed

representations simultaneously reproduced the co-variability in animals’ choice behavior and dopaminergic activity. Strikingly, these representations predict an unusual distribution of

response times that closely match animals’ behavior. These results inform how constraints of representational efficiency may be expressed in encoding representations of dynamic cognitive

variables used for reward-based computations. Access through your institution Buy or subscribe This is a preview of subscription content, access via your institution ACCESS OPTIONS Access

through your institution Access Nature and 54 other Nature Portfolio journals Get Nature+, our best-value online-access subscription $29.99 / 30 days cancel any time Learn more Subscribe to

this journal Receive 12 print issues and online access $209.00 per year only $17.42 per issue Learn more Buy this article * Purchase on SpringerLink * Instant access to full article PDF Buy

now Prices may be subject to local taxes which are calculated during checkout ADDITIONAL ACCESS OPTIONS: * Log in * Learn about institutional subscriptions * Read our FAQs * Contact customer

support SIMILAR CONTENT BEING VIEWED BY OTHERS DISTINCT VALUE COMPUTATIONS SUPPORT RAPID SEQUENTIAL DECISIONS Article Open access 21 November 2023 TEMPORAL REGULARITIES SHAPE PERCEPTUAL

DECISIONS AND STRIATAL DOPAMINE SIGNALS Article Open access 17 August 2024 DOPAMINE-INDEPENDENT EFFECT OF REWARDS ON CHOICES THROUGH HIDDEN-STATE INFERENCE Article Open access 12 January

2024 DATA AVAILABILITY The experimental data shown in this study are available through the original study by ref. 31. Details of this study are approved under the protocol approved by the

Champalimaud Foundation Animal Welfare Body (protocol number: 2017/013) and the Portuguese Veterinary General Board (Direcção-Geral de Veterinária, project approval number:

0421/000/000/2018) and in accordance with the European Union Directive 2010/63/EEC CODE AVAILABILITY All code for simulations reported in this study and some saved variables used to show the

model’s results are available at https://github.com/asma-motiwala/ITD-SNcDA-TDE. REFERENCES * Dayan, P. & Sejnowski, T. J. Td(_λ_) converges with probability 1. _Mach. Learn._ 14,

295–301 (1994). Google Scholar  * Sutton, R. S. Learning to predict by the methods of temporal differences. _Mach. Learn._ 3, 9–44 (1988). Google Scholar  * Bayer, H. M. & Glimcher, P.

W. Midbrain dopamine neurons encode a quantitative reward prediction error signal. _Neuron_ 47, 129–141 (2005). Article  CAS  PubMed  PubMed Central  Google Scholar  * Fiorillo, C. D.,

Tobler, P. N. & Schultz, W. Discrete coding of reward probability and uncertainty by dopamine neurons. _Science_ 299, 1898–1902 (2003). Article  CAS  PubMed  Google Scholar  * Schultz,

W., Dayan, P. & Montague, P. R.A neural substrate of prediction and reward. _Science_ 275, 1593–1599 (1997). Article  CAS  PubMed  Google Scholar  * Reynolds, J. N. J., Hyland, B. I.

& Wickens, J. R. A cellular mechanism of reward-related learning. _Nature_ 413, 67–70 (2001). Article  CAS  PubMed  Google Scholar  * Stauffer, W. R., Lak, A. & Schultz, W. Dopamine

reward prediction error responses reflect marginal utility. _Curr. Biol._ 24, 2491–2500 (2014). Article  CAS  PubMed  PubMed Central  Google Scholar  * Steinberg, E. E. et al. A causal link

between prediction errors, dopamine neurons and learning. _Nat. Neurosci._ 16, 966–973 (2013). Article  CAS  PubMed  PubMed Central  Google Scholar  * Niv, Y. & Langdon, A. Reinforcement

learning with Marr. _Curr. Opin. Behav. Sci._ 11, 67–73 (2016). Article  PubMed  PubMed Central  Google Scholar  * Watabe-Uchida, M., Eshel, N. & Uchida, N. Neural circuitry of reward

prediction error. _Annu. Rev. Neurosci._ 40, 373–394 (2017). Article  CAS  PubMed  PubMed Central  Google Scholar  * Daw, N. D., Courville, A. C. & Touretzky, D. S. Representation and

timing in theories of the dopamine system. _Neural Comput._ 18, 1637–1677 (2006). Article  PubMed  Google Scholar  * Ludvig, E. A., Sutton, R. S. & Kehoe, E. J. Stimulus representation

and the timing of reward-prediction errors in models of the dopamine system. _Neural Comput._ 20, 3034–3054 (2008). Article  PubMed  Google Scholar  * Suri, R. E. & Schultz, W. A neural

network model with dopamine-like reinforcement signal that learns a spatial delayed response task. _Neuroscience_ 91, 871–890 (1999). Article  CAS  PubMed  Google Scholar  * Botvinick, M.

M., Niv, Y. & Barto, A. G. Hierarchically organized behavior and its neural foundations: a reinforcement learning perspective. _Cognition_ 113, 262–280 (2009). Article  PubMed  Google

Scholar  * Starkweather, C. K., Babayan, B. M., Uchida, N. & Gershman, S. J. Dopamine reward prediction errors reflect hidden-state inference across time. _Nat. Neurosci._ 20, 581–589

(2017). Article  CAS  PubMed  PubMed Central  Google Scholar  * Russek, E. M., Momennejad, I., Botvinick, M. M., Gershman, S. J. & Daw, N. D. Predictive representations can link

model-based reinforcement learning to model-free mechanisms. _PLoS Comput. Biol._ 13, e1005768 (2017). Article  CAS  PubMed  PubMed Central  Google Scholar  * Gouvêa, T. S. et al. Striatal

dynamics explain duration judgments. _eLife_ 4, e11386 (2015). Article  PubMed  PubMed Central  Google Scholar  * Mello, G. B. M., Soares, S. & Paton, J. J. A scalable population code

for time in the striatum. _Curr. Biol._ 25, 1113–1122 (2015). Article  CAS  PubMed  Google Scholar  * Remington, E. D., Narain, D., Hosseini, E. A. & Jazayeri, M. Flexible sensorimotor

computations through rapid reconfiguration of cortical dynamics. _Neuron_ 98, 1005–1019 (2018). Article  CAS  PubMed  PubMed Central  Google Scholar  * Wang, J., Narain, D., Hosseini, E. A.

& Jazayeri, M. Flexible timing by temporal scaling of cortical responses. _Nat. Neurosci._ 21, 102–110 (2018). Article  CAS  PubMed  Google Scholar  * Atick, J. J. & Redlich, A. N.

What does the retina know about natural scenes? _Neural Comput._ 4, 196–210 (1992). Article  Google Scholar  * Lewicki, M. S. Efficient coding of natural sounds. _Nat. Neurosci._ 5, 356–363

(2002). Article  CAS  PubMed  Google Scholar  * Olshausen, B. A. & Field, D. J. Emergence of simple-cell receptive field properties by learning a sparse code for natural images. _Nature_

381, 607–609 (1996). Article  CAS  PubMed  Google Scholar  * Rieke, F., Bodnar, D. A., & Bialek, W. Naturalistic stimuli increase the rate and efficiency of information transmission by

primary auditory afferents. _Proc. Biol. Sci._ 262, 259–265 (1995). * Machens, C. K., Gollisch, T., Kolesnikova, O. & Herz, A. V. M. Testing the efficiency of sensory coding with optimal

stimulus ensembles. _Neuron_ 47, 447–456 (2005). Article  CAS  PubMed  Google Scholar  * Reinagel, P. & Zador, A. M. Natural scene statistics at the centre of gaze. _Network_ 10,

341–350 (1999). Google Scholar  * Salinas, E. How behavioral constraints may determine optimal sensory representations. _PLoS Biol._ 4, e387 (2006). Article  CAS  PubMed  PubMed Central 

Google Scholar  * Botvinick, M., Weinstein, A., Solway, A. & Barto, A. Reinforcement learning, efficient coding, and the statistics of natural tasks. _Curr. Opin. Behav. Sci._ 5, 71–77

(2015). Article  Google Scholar  * Summerfield, C. & Tsetsos, K. Building bridges between perceptual and economic decision-making: neural and computational mechanisms. _Front. Neurosci._

6, 70 (2012). Article  PubMed  PubMed Central  Google Scholar  * Louie, K. & Glimcher, P. W. Efficient coding and the neural representation of value. _Ann. N Y Acad. Sci._ 1251, 13–32

(2012). Article  PubMed  Google Scholar  * Soares, S., Atallah, B. V. & Paton, J. J. Midbrain dopamine neurons control judgment of time. _Science_ 354, 1273–1277 (2016). Article  CAS 

PubMed  Google Scholar  * Kepecs, A., Uchida, N., Zariwala, H. A. & Mainen, Z. F. Neural correlates, computation and behavioural impact of decision confidence. _Nature_ 455, 227–231

(2008). Article  CAS  PubMed  Google Scholar  * Kiani, R. & Shadlen, M. N. Representation of confidence associated with a decision by neurons in the parietal cortex. _Science_ 324,

759–764 (2009). Article  CAS  PubMed  PubMed Central  Google Scholar  * Lak, A., Nomoto, K., Keramati, M., Sakagami, M. & Kepecs, A. Midbrain dopamine neurons signal belief in choice

accuracy during a perceptual decision. _Curr. Biol._ 27, 821–832 (2017). Article  CAS  PubMed  PubMed Central  Google Scholar  * Janssen, P. & Shadlen, M. N. A representation of the

hazard rate of elapsed time in macaque area lip. _Nat. Neurosci._ 8, 234–241 (2005). Article  CAS  PubMed  Google Scholar  * Fiorillo, C. D., Newsome, W. T. & Schultz, W. The temporal

precision of reward prediction in dopamine neurons. _Nat. Neurosci._ 11, 966–973 (2008). Article  CAS  PubMed  Google Scholar  * Pasquereau, B. & Turner, R. S. Dopamine neurons encode

errors in predicting movement trigger occurrence. _J. Neurophysiol._ 113, 1110–1123 (2015). Article  PubMed  Google Scholar  * Gibbon, J. & Church, R. M. Representation of time.

_Cognition_ 37, 23–54 (1990). Article  CAS  PubMed  Google Scholar  * Joel, D., Niv, Y. & Ruppin, E. Actor–critic models of the basal ganglia: new anatomical and computational

perspectives. _Neural Netw._ 15, 535–547 (2002). Article  PubMed  Google Scholar  * Khamassi, M., Lachèze, L., Girard, B., Berthoz, A. & Guillot, A. Actor–critic models of reinforcement

learning in the basal ganglia: from natural to artificial rats. _Adaptive Behavior_ 13, 131–148 (2005). Article  Google Scholar  * Roitman, J. D. & Shadlen, M. N. Response of neurons in

the lateral intraparietal area during a combined visual discrimination reaction time task. _J. Neurosci._ 22, 9475–9489 (2002). Article  CAS  PubMed  PubMed Central  Google Scholar  *

Wimmer, G. E., Daw, N. D. & Shohamy, D. Generalization of value in reinforcement learning by humans. _Eur. J. Neurosci._ 35, 1092–1104 (2012). Article  PubMed  PubMed Central  Google

Scholar  * Foster, D. & Dayan, P. Structure in the space of value functions. _Mach. Learn._ 49, 325–346 (2002). Article  Google Scholar  * Solway, A. et al. Optimal behavioral hierarchy.

_PLoS Comput. Biol._ 10, e1003779 (2014). Article  CAS  PubMed  PubMed Central  Google Scholar  * Mastrogiuseppe, F. & Ostojic, S. Linking connectivity, dynamics, and computations in

low-rank recurrent neural networks. _Neuron_ 99, 609–623 (2018). Article  CAS  PubMed  Google Scholar  * Kao, T.-C., Sadabadi, M. S. & Hennequin, G. Optimal anticipatory control as a

theory of motor preparation: a thalamo-cortical circuit model. _Neuron_ 109, 1567–1581 (2021). Article  CAS  PubMed  PubMed Central  Google Scholar  * Mnih, V. et al. Human-level control

through deep reinforcement learning. _Nature_ 518, 529–533 (2015). Article  CAS  PubMed  Google Scholar  * Song, H. F., Yang, G. R. & Wang, X.-J. Reward-based training of recurrent

neural networks for cognitive and value-based tasks. _eLife_ 6, e21492 (2017). Article  PubMed  PubMed Central  Google Scholar  * Wang, J. X. et al. Prefrontal cortex as a meta-reinforcement

learning system. _Nat. Neurosci._ 21, 860–868 (2018). Article  CAS  PubMed  Google Scholar  * Sutton, R. S. & Barto, A. G. _Reinforcement Learning: An Introduction_ (MIT Press, 2018). *

Baird, L. C. Advantage updating. Technical Report WL-TR-93-1146. Wright Laboratory, Wright-Patterson Air Force Base.

https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.135.9434&rep=rep1&type=pdf (1993). Download references ACKNOWLEDGEMENTS We thank J. Semedo and A. Renart for several helpful

discussions and feedback on the manuscript. We thank members of the Paton laboratory for several helpful discussions. We also thank S. Berger for feedback on the manuscript. This work was

developed with support from the research infrastructure Congento, co-financed by Lisboa Regional Operational Programme (Lisboa2020), under the PORTUGAL 2020 Partnership Agreement, through

the European Regional Development Fund and Fundação para a Ciência e Tecnologia (Portugal), under project LISBOA-01-0145-FEDER-022170. The work was funded by a Howard Hughes Medical

Institute International Research Scholar Award to J.J.P (55008745), a European Research Council Consolidator grant (DYCOCIRC - REP-772339-1) to J.J.P., a BIAL bursary for scientific research

to J.J.P. (193/2016) and internal support from the Champalimaud Foundation. The work was also supported by a National Institutes of Health U01 grant (NS094288) to C.K.M. and the Fundação

para Ciência e Tecnologia (SFRH/BD/52214/2013) to A.M. The funders had no role in study design, data collection and analysis, decision to publish or preparation of manuscript. AUTHOR

INFORMATION Author notes * Asma Motiwala Present address: Department of Electrical and Computer Engineering, Carnegie Mellon University, Pittsburgh, PA, USA * Sofia Soares Present address:

Harvard Medical School, Boston, MA, USA * These authors contributed equally: Joseph Paton, Christian Machens. AUTHORS AND AFFILIATIONS * Champalimaud Neuroscience Programme, Champalimaud

Foundation, Lisbon, Portugal Asma Motiwala, Sofia Soares, Bassam V. Atallah, Joseph J. Paton & Christian K. Machens Authors * Asma Motiwala View author publications You can also search

for this author inPubMed Google Scholar * Sofia Soares View author publications You can also search for this author inPubMed Google Scholar * Bassam V. Atallah View author publications You

can also search for this author inPubMed Google Scholar * Joseph J. Paton View author publications You can also search for this author inPubMed Google Scholar * Christian K. Machens View

author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS A.M., J.J.P. and C.K.M. designed the study. A.M. performed all analyses and simulations. S.S.,

B.V.A. and J.J.P. designed and S.S. and B.A. performed the behavioral and photometry experiments. A.M., J.P. and C.K.M. wrote the manuscript. J.J.P. and C.K.M. contributed equally to this

work. CORRESPONDING AUTHORS Correspondence to Asma Motiwala, Joseph J. Paton or Christian K. Machens. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. PEER

REVIEW PEER REVIEW INFORMATION _Nature Neuroscience_ thanks the anonymous reviewers for their contribution to the peer review of this work. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer

Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. EXTENDED DATA EXTENDED DATA FIG. 1 SCHEMATIC TO ILLUSTRATE HOW VARIOUS TASK

EVENTS INFLUENCE REWARD EXPECTATIONS. Let us assume the duration of intervals presented is uniformly distributed between 0 to 3 sec. and that choices are reported only at interval offset. In

this case, the agent needs to estimate value functions over two sets of states, one during the interval and the other at interval offset. Let us assume the reward amount is 1, in this case

the value at interval offset _C_(_z_) will be equal to the probability of reporting the correct choice for that interval estimate. During the interval, the value function is a weighted sum

of the value of interval offset at that time and the value of being in the interval at later times. The weighting factor is given by the probability of transitioning to each of these states,

that is, \(V(z)=p({{z}^{\prime}={{{{{\rm{interval}}}}}}\,{{{{{\rm{offset}}}}}}| z})* C(z)+\gamma\)\(* p\left({z}^{\prime}\ne {{{{{\rm{interval}}}}}}\,{{{{{\rm{offset}}}}}}| z\right)*

V({z}^{\prime})\), where \({z}^{\prime}\) is the successor state. (A-D) If we assume that the agent does not explicitly encode the distribution of interval durations, but does encode an

estimate of choice accuracy at interval offset, the hazard rate encoded by the agent is zero for all internal estimates of time (shown in panel a), and its estimate of value during the

interval will always be zero (shown in panel c). Its estimate of value at interval offset is equal to the probability with which it will correctly report interval duration (shown in panel b)

and the resulting RPEs at interval offset will reflect only choice accuracy (shown in panel d). (E-H) Let us now assume that the agent encodes the distribution of interval durations, but

does not encode choice accuracy. The probability of detecting interval offset at any estimated time z given that no interval offset was detected for all \({z}^{\prime} < z\) is given by

the hazard rate of interval offset, H(z). In the case of uniformly distributed interval durations, H(z) is shown in panel e. In this case the value function during the interval is

monotonically increasing. If there was no time discounting (that is, _γ_ = 1), this value function would be 1 for the entire interval. For time discounted rewards (that is, 0 < < _γ_ 

< 1), the value function simply reflects the fact that early in the interval the agent expects rewards to be, on average, further in the future and hence more time-discounted than later

in the interval (as shown in panel g). Since we assumed here that the agent does not encode choice accuracy, reward expectations from interval offset states are constant (panel f).

Consequently, RPEs at interval offset will be monotonically decreasing with elapsed time (as shown in panel h). (I-L) Finally, if we assume that the agent encodes, both, choice accuracy and

the distribution of interval durations, we see that the estimated value at interval offset is the same as when the agent only encodes choice accuracy (shown in panel j). However, the value

function during the interval now reflects a combination of choice accuracy and the hazard rate of interval offsets, that is \(V(z)=H(z)* C(z)+\gamma * (1-H(z))* V({z}^{\prime})\) (shown in

panel k). Consequently, the RPEs will also reflect both choice accuracy and the hazard rate of interval offset (as shown in panel l). EXTENDED DATA FIG. 2 SCHEMATIC TO ILLUSTRATE HOW THE

OVERALL PROFILE OF RPES AT INTERVAL OFFSET DETERMINES DIFFERENCES BETWEEN PSYCHOMETRIC FUNCTIONS FOR LOW AND HIGH RPES TRIALS. Each row shows how over or underestimating elapsed time (shown

in column 1) changes RPEs at any possible interval duration (column 2), the probability of reporting choice ‘long’ (column 3) and how magnitude of RPEs relate to the probability of choice

‘long’ (column 4). The top row shows the case when reward expectations are estimated only based on choice accuracy (as shown in Supp Fig 1a-d), the middle row shows the case when reward

expectations only reflect the hazard rate of interval offset (as shown in Supp Fig 1e-h) and the bottom row shows the case when reward expectations are estimated based on choice accuracy as

well as hazard rate of interval offset (as shown in Supp Fig 1i-l). (Column 1) Let’s consider two example types of trials (shown in panels a,e,i), one in which elapsed time is underestimated

(_z_ < _t_, shown by the blue line) and the other overestimates elapsed time (_z_ > _t_, shown by the red line). (Column 2) For these two types of trials, RPEs at interval offsets for

all possible interval durations are shown in the second column (each row corresponds to each of the three possibilities for how the agent might estimate reward expectations as a function of

task events shown in Supp Fig 1d,h,l). In each panel, for every time step, the trial on which RPE is lower than the other is highlighted in yellow. In panel (B), when RPEs result from

reward expectations that only take into account choice accuracy, for all time points before the decision boundary, trials on which elapsed time is overestimated will have lower RPEs than

trials on which elapsed time is underestimated. On the other hand, for all time points after the decision boundary, trials on which elapsed time is underestimated will have lower RPEs. In

panel (F), when RPEs are driven only due to the hazard rate of interval offset, for all time points trials on which elapsed time is overestimated will have lower RPEs. Finally, in panel (J),

when RPEs reflect both choice accuracy and hazard rate of interval offset, RPEs are lower on trials on which elapsed time is overestimated on the short side of the boundary. On the long

side of the boundary, close to the boundary, trials on which elapsed time is underestimated have lower RPEs. However, for estimates much longer than the boundary, we see trials on which

elapsed time is overestimated have lower RPEs. (Column 3) If the agent’s choices change as a function of it’s internal estimates of elapsed time, for the two example trial types shown here,

the psychometric function of the agent will also be different. When the agent underestimates elapsed time (blue curve), the psychometric curve will be biased towards ‘short’ choices (that is

it will show a rightward shift). Similarly, if the agent overestimates time (red curve), the psychometric curve will be biased towards ‘long’ choices (that is will be shifted left). To

establish the relationship between magnitude of RPE at any given estimated time of interval offset and the probability of choices the agent will report, for each of the trial types, all time

points at which RPE was lower on that trial type (shown by the yellow highlights in the second column) are also highlighted in yellow. In panel (C), we see that for all time points before

the boundary, the probability of choosing long is higher for most segments highlighted yellow. For all time points after the decision boundary, we see that the probability of choosing short

is higher for all segments highlighted in yellow. In panel (G), we see that for all interval durations, trials that had lower RPEs have a higher probability of reporting the interval as

‘long’. Finally, in panel (K), we see that for all interval durations before the boundary, low RPE trials have a higher probability of reporting choice ‘long’ and the opposite is true after

the decision boundary. (Column 4) For each of the panels c,g and k, for all time points on either side of the boundary we ask: what is the average of the psychometric curves highlighted in

yellow. (D) In panel c, we see that on the short side of the boundary, for most time points the red psychometric curve is highlighted and the average of the highlighted segments of the curve

is shown by the solid yellow marker in the top panel in column d. For time points longer than the boundary, we see in panel c that for most time points, the blue curve is highlighted and

the average of that segment of the psychometric curve is shown by the yellow marker on the long side if the boundary in panel d. The green points in panel d show the averages of the curves

in panel c on either side of the boundary that are not highlighted and correspond to time points at which the RPEs (shown in panel b) are higher. In other words, when RPEs are driven only

due to choice accuracy, lower RPE in general are associated with low choice variability and hence, we would predict the psychometric curves for low and high RPE trials, in this case, to show

a difference in slope. (H) Following the same steps for the middle row (panels e-h), we find that when RPEs are driven only by the hazard rate of interval offset, low RPEs correlate with

higher probability of reporting long irrespective of which side of the boundary the interval offset lies. Thus, in this case we would predict a change in bias in psychometric functions for

low and high RPE trials. (L) Finally, when RPEs reflect both choice accuracy as well as the hazard rate of interval offset, following the same steps we find that the psychometric curves for

low and high RPE trials show a change in slope. EXTENDED DATA FIG. 3 DISTRIBUTIONS OF INTERNAL ESTIMATES OF ELAPSED TIME AT INTERVAL OFFSET. Each curve shows the distribution of the agent’s

internal estimates of elapsed time since interval onset at interval offsets for each of the interval durations presented in the task. The color of the curve indicates which interval duration

the distribution corresponds to. We see that these distributions of internal estimates get wider with the length of the interval duration at which the estimates are recorded. This is due to

scalar variability implemented in the dynamics with which the latent variable and hence internal estimates of elapsed time evolve in the model. EXTENDED DATA FIG. 4 AVERAGE REWARD

PREDICTION ERRORS AT INTERVAL OFFSET AND DIFFERENCE IN PSYCHOMETRIC FUNCTIONS OF TRIALS GROUPED BASED ON THE MAGNITUDE OF RPES, FOR VARYING DEGREES OF COMPRESSION IN THE REPRESENTATION USED.

(Top) We see that the profile of average RPEs does not vary considerably for the different degrees of compression in the basis functions used to estimate value functions. (Bottom) We see

that for the efficient representation (_λ_ = 1), the difference in the psychometric curve has the same sign of all the stimuli presented. This corresponds to a change in bias and an overall

shift along the stimulus axis between the two psychometric functions (as seen in the data, shown in Fig. 2b). On the other hand, for the unambiguous representation (_λ_ = 0), the difference

in the psychometric function changes sign for stimuli on different sides of the boundary. This corresponds to a change in slope between the two psychometric functions. This is consistent

with the results from the simple model shown in Supp. Figure 2l where the psychometric curves cross around the decision boundary. We see that only for representations that are very close to

the most efficient version do the psychometric functions show a difference in bias as is observed in the data. EXTENDED DATA FIG. 5 QUANTIFICATION OF AVERAGE RPE AT INTERVAL OFFSET FOR A

RANGE OF MODEL PARAMETERS SHOWS THAT THE MAIN FEATURES OF THE AVERAGE RPE PROFILE CAN BE REPRODUCED BY REPRESENTATIONS OF ALL DEGREES OF COMPRESSION. (A-C) All of the panels in the top row

show the average RPE at interval offset using the efficient representation. Each panel shows which feature of the RPE is being quantified in the corresponding column. (A) The dashed lines

show average RPE for all short intervals (in purple) and all long intervals (in brown). (B) The dark and light purple dots show the average RPE magnitude for short easy and short

near-boundary stimuli respectively. (C) The dark and light brown points show the average RPE magnitude for long easy and long near-boundary stimuli respectively. (D,G,J) All panels show the

difference between average RPE at interval offset for long and short interval durations. This difference is plotted as a function of model parameters that control stochasticity of the policy

(_α_) and temporal variability (_σ_) for the efficient representation, an intermediate representation and the unambiguous representation. In (D) we see qualifications of RPEs when using the

efficient representation (_λ_ = 1), in (G) using an intermediate representation (_λ_ = 0.5) and in (J) using the unambiguous representation (_λ_ = 0). For all model parameters and all

degrees of compression of the representation, we see that average RPEs are higher for short intervals than long intervals. This is consistent with the observed magnitude of DA activity at

interval offset. The difference between average z-scored DA magnitude for short vs long interval durations was 0.52. The red star in the heat maps indicates the parameter combination with

which the plots in the top row were generated. (E,H,K) All heat maps in this column show the difference in the magnitude of RPE between easy and near-boundary short interval durations. In

(E) we see qualifications of RPEs when using the efficient representation (_λ_ = 1), in (H) using an intermediate representation (_λ_ = 0.5) and in (K) using the unambiguous representation

(_λ_ = 0). For all model parameters and all degrees of compression of the representation, we see that average RPEs are higher for easy short intervals than near-boundary short intervals.

This is consistent with observed DA magnitude in experiments. The difference between average z-scored DA magnitude for easy vs near-boundary short intervals was 0.50. (F,I,J) All heat maps

in this column show the difference in the magnitude of RPE between easy and near-boundary long interval durations. We see that average RPEs are only slightly higher for long easy intervals

than long near-boundary intervals. Over a large range of parameter combinations, the difference in RPE magnitude between easy and near-boundary stimuli is higher for short intervals than

long intervals. This is again consistent with observed DA magnitude in experiments. The difference between average z-scored DA magnitude for easy vs near-boundary long intervals was 0.29.

Overall, these results show that average DA responses are well captured by the model irrespective of the efficiency of the representation used. EXTENDED DATA FIG. 6 QUANTIFICATION OF

PSYCHOMETRIC CURVES SPLIT BY MAGNITUDE OF RPE AT INTERVAL OFFSET FOR A RANGE OF MODEL PARAMETERS SHOWS THAT THE CHANGE IN BIAS OBSERVED IN DATA IS BEST REPRODUCED WHEN USING THE EFFICIENT

REPRESENTATION. (A-B) Panels in the top row show psychometric curves of trials split by high and low RPE at interval offset. Each panel shows which feature of these psychometric curves is

quantified and plotted in the heatmaps in the corresponding columns. (A) The large dots show, for each psychometric function, the interval duration at which the probability of reporting a

long choice would be 0.5. We use this estimate to quantify bias in each psychometric function. (B) For each psychometric function, we characterize the interval durations that would

correspond to 0.25 and 0.75 probability of reporting a long choice. We use the range between these two values to quantify the sensitivity of each of the two psychometric functions. (C,E,G)

In each of these panels, the heat maps show the difference in bias between the psychometric curves of high and low RPE trials. In (C) we see the difference in bias over a range of model

parameters using the efficient representation (_λ_ = 1), in (E) using an intermediate representation (_λ_ = 0.5) and in (G) using the unambiguous representation (_λ_ = 0). For all model

parameters we see that the difference in bias is largest when using the efficient representation as compared to that of the intermediate and unambiguous representations. The red star in the

heat maps indicates the parameter combination with which the plots in the top row were generated. (D,F,H) In each of these panels, the heat maps show the difference in the sensitivity

between the psychometric curves for high vs low RPE trials. In (D) we see the difference in sensitivity over a range of model parameters using the efficient representation (_λ_ = 1), in (F)

using an intermediate representation (_λ_ = 0.5) and in (H) using the unambiguous representation (_λ_ = 0). For all model parameters we see that the difference in sensitivity is smallest

when using the efficient representation as compared to that of the intermediate and unambiguous representations. Overall, these quantifications show that for a large range of parameters, the

efficient representation yields the greatest similarity to experimental data, that is a much larger difference in bias in psychometric curves for trials split by high and low DA magnitude

at interval offset as compared to the difference in sensitivity. When we split trials based on observed magnitude of DA activity at interval offset into low and high DA, we find that the

difference in bias was 0.28 sec and the difference in sensitivity was 0.05 sec. EXTENDED DATA FIG. 7 DISTRIBUTIONS OF RPES AT INTERVAL OFFSET SHOW WHY COMPRESSION IN THE REPRESENTATION

CAUSES PSYCHOMETRIC CURVES SPLIT BY RPE MAGNITUDE TO BE DIFFERENT. To understand why the asymmetry in the value function at interval offset using the efficient representation (shown in Fig. 

7e) reproduces the change in bias observed in the psychometric curves of low and high DA trials in animals, let us consider how internal estimates of time, RPEs and choices covary for each

of the two near-boundary intervals. Let us consider the results obtained using the unambiguous representation. For each of these intervals, the agent’s estimate of elapsed time will vary

from trial-to-trial as described by the two distributions shown in (A) and (D). We recall that the agent’s decisions are based entirely on its internal estimates of elapsed time: when the

estimate is shorter (or longer) than the boundary, the agent will report choice ‘short’ (or ‘long’) with higher probability. We can therefore split each of the distributions based on the

choice of the agent ((A) and (D) red and blue areas). This procedure creates four groups of trials, given by the two near-boundary intervals and the two choices of the agent. Within each

group, the variability in time estimates gives rise to associated variability in RPEs. The four resulting distributions of RPEs are shown in (B) and (E). Here, the two panels group trials

according to the presented interval, and the red and blue RPE distributions in each panel correspond to trials grouped according to the animal’s choice. Using these groupings, we can now

study how high or low RPE trials relate to behavior. To do so, we first define high (or low) RPE trials for a given interval as all trials with RPEs greater (or smaller) than the median RPE

for that interval (indicated by the dashed line). The fraction of long choices falling into the high (or low) RPE trials shown in (C) and (F) correspond to points at the near boundary

intervals in the psychometric functions shown in Fig. 4c (which are for all interval durations). For the RL agent using the unambiguous representation, RPEs on incorrect trials are on

average lower than RPEs on correct trials (B) and (E). In turn, if we split all trials based on the magnitude of RPEs, irrespective of the interval, we find that the agent made more mistakes

on low RPE trials compared to high RPE trials. Thus, the psychometric curves for these two groups of trials show a larger difference in slope and cross each other around the decision

boundary (B) and (E). For the RL agent using the efficient representation, the picture is very different (G-L). Here we find that RPEs are on average lower when the agent reports choices as

long, irrespective of the interval (H) and (K). Consequently, the psychometric functions for high and low RPEs show a larger change in bias and do not cross each other near the boundary (I)

and (L). EXTENDED DATA FIG. 8 THE EFFICIENT REPRESENTATION INCENTIVISES PROCRASTINATION OF CHOICES FOR LONG INTERVAL ESTIMATES CLOSE TO THE DECISION BOUNDARY. (A) The heat map shows the

value function learnt using the efficient representation when the agent is required to report choices immediately after interval offset. The purple and mustard yellow lines show example

trajectories the agent would take through the state space if it withheld choice for the entire trial for an example ‘short’ (purple) and ‘long’ (yellow) interval. (B-C) The sequence of state

values that the agent will encounter when it follows the purple and yellow trajectories, respectively, shown in (A). The triangle markers indicate the timesteps at which the agent

encountered interval offset during these trials. Let’s denote the interval offset states as z1 and the subsequent state that the agent transitions to as z2. The red arrows show the

transition between z1 and z2 for the example trajectories shown in (B-C). (B) We see that after an estimated ‘short’ interval, withholding choice would result in the value function to

decrease and hence incur negative RPEs. However, the average reward obtained from reporting a choice immediately would be equal to the value of the interval offset state z1 and will, on

average, incur zero RPEs. Hence the agent is discouraged from withholding choice when estimating an interval to be ‘short’. (C) On the other hand, for intervals estimated as near-boundary

‘long’, withholding choices results in incurring positive RPEs. If the agent reported a choice immediately, it would on average receive rewards equal to the value function at z1 and incur

zero RPEs in doing so. Hence the agent is incentivised to withhold choices for long near-boundary interval estimates. On these trials, when the agent transitions from z1 to z2 by withholding

choice actions, the value of z1 will be updated closer to the value of state z2 based on the TD update equation _V_(_z_1) ← _V_(_z_1) + _α_(_γ__V_(_z_2) − _V_(_z_1)). Moreover, when the

agent reports a choice action at z2 after transitioning from z1 to z2, the average reward it will receive from z2 will be lower than if the interval offset had been presented at z2.

trial-to-trial variability in the latent variable z will lead to incorrect estimates of the category (‘short’ vs ‘long’) of intervals presented closer to the decision boundary (such as z1)

than those further away from it (such as z2). Consequently, trial-to-trial variability in choices at z2 will be lower if those choices are from trials where the agent’s estimate at interval

offset is z2 than if choices at z2 are reported on trials in which agent’s estimate at interval offset is either z2 or z1. Thus, TD-updates on the long side of the decision boundary lead to

a flattening of the value function in the efficient model due to procrastination of choices. EXTENDED DATA FIG. 9 AVERAGE RESPONSE TIMES ACCORDING TO THE AGENT’S CHOICE FOR VARYING DEGREES

OF COMPRESSION IN THE REPRESENTATION. The agent has short response times for all stimuli when choosing short. The profile is very similar for all degrees of compression in the representation

used. However, the profile of average response times when the agent chooses long changes greatly with the degree of compression in the representation. Only when using efficient

representation (_λ_ = 1), do we see response times vary strongly as a function of interval duration and decrease with the length of the interval duration on trials with ‘long’ choices as

seen in the data (shown in Fig. 8c). EXTENDED DATA FIG. 10 QUANTIFICATION OF AVERAGE RESPONSE TIMES FOR A RANGE OF MODEL PARAMETERS SHOWS THAT THE RESPONSE TIME PROFILE OBSERVED IN ANIMALS

IS BEST REPRODUCED BY THE MODEL WHEN USING THE EFFICIENT MODEL. (A-C) All of the panels in the top row show the average response times of the model when using the efficient representation.

The solid red line shows average response times for all interval durations when the agent makes long choices and solid blue lines show average response times when the agent makes short

choices. Each panel also shows which feature of the response time profile is being quantified in the corresponding column. (A) The dashed lines show average RTs for all short choices (in

blue) and all long choices (in red). (B) The two red dashed line segments show the average RTs for long choices for short and long interval durations presented. (C) The two blue dashed line

segments show the average RTs for short choices for short and long interval durations presented. (D,G,J) All heat maps show the difference in average response times for all long vs short

choices. This difference is plotted for a range of parameters that control temporal variability and stochasticity of the agent’s policy. In (D) we see the difference plotted for using the

efficient representation (_λ_ = 1), in (G) using an intermediate representation (_λ_ = 0.5) and in (J) using the unambiguous representation (_λ_ = 0). For all model parameters we see that

the difference in average RTs between long and short choices is largest using the efficient representation. (E,H,K) All heat maps show the difference in average RTs for short vs long

interval durations when the agent reported long choices. In (E) we see the difference plotted for using the efficient representation (_λ_ = 1), in (H) using an intermediate representation

(_λ_ = 0.5) and in (K) using the unambiguous representation (_λ_ = 0). We see, over a range of parameters, that the difference in average RTs for long vs short intervals, when the agent

reports long choices, is largest for the efficient representation. The red star in the heat maps indicates the parameter combination with which the plots in the top row were generated.

(F,I,L) All heat maps show the difference in average RTs for short vs long interval durations when the agent reported short choices. In (F) we see the difference plotted for using the

efficient representation (_λ_ = 1), in (I) using an intermediate representation (_λ_ = 0.5) and in (L) using the unambiguous representation (_λ_ = 0). We see, over a range of parameters,

that the difference in average RTs for long vs short intervals, when the agent reports long choices, is very close to zero and the overall response profile is very similar across all degrees

of compression in the representation. We also see that the difference in RTs for long vs short intervals is larger when the agent makes long choices as opposed to when the agent makes short

choices (compare second and third columns). The most surprising feature of animals’ behaviour during this task is that their response times do not have the ‘x-shaped profile’ previously

reported in other two-alternative forced choice tasks. Instead we find that animals have longer response times for long choices for all interval durations (the difference between average RTs

for long vs short choices is 446 ms), that response times for long choices negatively correlate with interval duration (the difference in average RTs for long choices for long vs short

interval durations was 651 ms) and that responses for short choices were more similar for long and short interval durations (the difference in average RTs for long choices for long vs short

interval durations was -96 ms). Overall, we see that the model response times when using the efficient model show the main features observed in animals’ RTs and that this is not true when

the model using the unambiguous or more intermediate efficiency representations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION Supplementary Figs. 1 and 2 REPORTING SUMMARY RIGHTS AND

PERMISSIONS Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Motiwala, A., Soares, S., Atallah, B.V. _et al._ Efficient coding of cognitive variables underlies dopamine response

and choice behavior. _Nat Neurosci_ 25, 738–748 (2022). https://doi.org/10.1038/s41593-022-01085-7 Download citation * Received: 10 June 2020 * Accepted: 26 April 2022 * Published: 06 June

2022 * Issue Date: June 2022 * DOI: https://doi.org/10.1038/s41593-022-01085-7 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable

link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative