Raman-phonon-polariton condensation in a transversely pumped cavity

ABSTRACT Phonon polaritons are hybrid states of light and matter that are typically realised when optically active phonons couple strongly to photons. We suggest a new approach to realising

phonon polaritons, by employing a transverse-pumping Raman scheme, as used in experiments on cold atoms in optical cavities. This approach allows hybridisation between an optical cavity mode

and any Raman-active phonon mode. Moreover, this approach enables one to tune the effective phonon–photon coupling by changing the strength of the transverse pumping light. We show that

such a system may realise a phonon-polariton condensate. To do this, we find the stationary states and use Floquet theory to determine their stability. We thus identify distinct superradiant

and lasing states in which the polariton modes are macroscopically populated. We map out the phase diagram of these states as a function of pump frequencies and strengths. Using parameters

for transition metal dichalcogenides, we show that realisation of these phases may be practicably obtainable. The ability to manipulate phonon mode frequencies and attain steady-state

populations of selected phonon modes provides a new tool for engineering correlated states of electrons. SIMILAR CONTENT BEING VIEWED BY OTHERS POLARITON-DRIVEN PHONON LASER Article Open

access 11 September 2020 THEORY OF TERAHERTZ PUMP OPTICAL PROBE SPECTROSCOPY OF PHONON POLARITONS IN NONCENTROSYMMETRIC SYSTEMS Article Open access 01 May 2025 TERAHERTZ DISPLACIVE

EXCITATION OF A COHERENT RAMAN-ACTIVE PHONON IN V2O3 Article Open access 28 April 2022 INTRODUCTION Phonon polaritons result from strong coupling between light and lattice vibrations,

leading to new normal modes with hybrid properties of both constituents1. Because phonons play an essential role in material properties—including mediating phases such as

superconductivity—manipulating phonon properties by coupling to light is an intriguing prospect2. However, phonons are typically in the terahertz (THz) or infrared range, and direct strong

coupling requires cavities supporting THz or infrared cavity modes. Moreover, only optically active phonon modes—i.e., those with a dipole matrix element—can couple directly to light. In

many cases, relevant phonon modes may not be optically active; see e.g.3. As we demonstrate further below, this restriction can be overcome by using a Raman pumping scheme. That is, one

couples to the phonons via a two-photon transition involving cross terms between cavity photons and an external pump. This engineers an effective coupling between optical cavity photons and

terahertz phonons. Raman-driving schemes4 have proven highly fruitful for experiments involving cold atoms in optical cavities. Crucially, such schemes realise a scenario that may be

referred to as “synthetic cavity QED,” in which one can control the strength of matter-light coupling as well as the effective energies of the matter and light degrees of freedom. Following

the original proposal4, this enabled the realisation5 of the Dicke-Hepp-Lieb superradiance transition6,7,8. Further extensions of this core idea of Raman driving to multimode confocal

cavities9 have introduced tunable-range10 and sign-changing interactions11 to cavity QED, enabling the realisation of an optical lattice with sound modes12 and replica-symmetry breaking in a

spin glass13. See the reviews14,15 for further discussion. Our aim in this manuscript is to explore how the power and flexibility of Raman-driving can be extended to solid-state systems. As

noted above, being able to manipulate the properties of solid-state phonon modes is of significant interest due to the possibility of engineering correlated electronic phases. Using

transient light pulses to modify phonon modes has been central to proposals for, and realisations of, light-induced phase transitions in cuprates and other superconductors3,16,17,18. Such

results rely on direct, terahertz coupling of light to the phonons in the transient, pulsed-laser regime, and this inevitably causes heating while posing challenges to those attempting to

interpret the results. This has led to proposals to instead use strong coupling to infrared or THz cavities19,20, including a variety of proposals of how cavity QED may enhance

superconductivity21,22,23. Even with a cavity, the coupling is restricted to optically active modes. To overcome this, Raman driving schemes are required; see Ref. 24 for an alternative

Raman scheme providing parametric coupling between a THz photon and phonon. In this paper, we show that it is possible to achieve a superradiant phase—i.e., a phonon-polariton

condensate—using a continuous-wave Raman driving scheme coupling a phonon to an optical-frequency cavity mode. We present a model for independent, driven excitons in an optical cavity and

use the mean-field ansatz to show that sufficiently strong driving leads to an instability of the normal phase, understood to be the phase with no macroscopic population of the cavity. In

contrast to Raman-driving schemes for cold atoms, we find that adiabatic elimination of the exciton states is not quantitatively accurate for the parameters relevant to the materials we

study in this work. This requires us to directly model the periodically driven system, and to use Floquet analysis to understand the stability of states. We show that the instability can

take two forms, either due to superradiance or due to lasing, and we describe the features of each. We present the phase diagram for the model and discuss the effect of different parameters.

Our model is inspired by transition metal dichalcogenides (TMDs), particularly TMD monolayers; these have attracted much attention for their optoelectronic properties25. Key to the results

below is that they host sharp26, strongly bound, optically active excitons (electron-hole pairs)27,28 that couple to sufficiently long-lived optical phonons with a Huang-Rhys parameter of

approximately unity29,30. The model presented in this paper is, however, not limited to TMD materials, but presents a general approach for how Raman-driving may be used in solid-state

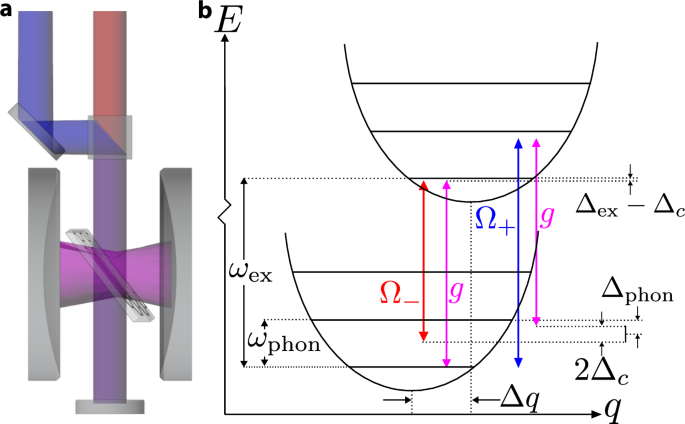
contexts. Hence the results below may be applied to more exotic few-layer and twisted multilayer materials. RESULTS MODEL: PHONONS AND DRIVEN EXCITONS IN A CAVITY We consider a model that

involves the interaction of cavity photons \(\hat{a}\), excitons \({\hat{X}}_{j}\), and phonons \({\hat{b}}_{j}\). Our model considers explicit exciton-photon coupling (including optical

driving of the excitons by the pumps) and exciton-phonon coupling. As discussed further below, this leads to an effective Raman coupling between phonons and photons; however, in contrast to

other Raman-driven schemes4, we will not adiabatically eliminate the excitons. To simplify the calculation, we consider the case of a single-mode optical cavity. We will remark later on how

these results might change in a multimode cavity. Furthermore, we consider a model of quasilocalised excitons on sites labelled _j_, each with an associated phonon mode. Such a model is an

approximation to the full description of TMD materials, in which both excitons and phonons are delocalised. However, such a model is a reasonable first approximation when considering

excitons and phonons with relatively flat dispersions, which can be the case for TMDs28,31. Setting _ℏ_ = 1 throughout, this model takes the form \(\hat{H}={\omega }_{c}{\hat{a}}^{{\dagger}

}\hat{a}+{\sum }_{j = 1}^{N}{\hat{H}}_{{{\rm{mat}}},j}\), where the matter Hamiltonian for each site _j_ is $$\begin{array}{l}{\hat{H}}_{{{\rm{mat}}},j}={\omega

}_{{{\rm{ex}}}}{\hat{X}}_{j}^{{\dagger} }{\hat{X}}_{j}+{\omega }_{{{\rm{phon}}}}\left[{\hat{b}}_{j}^{{\dagger} }{\hat{b}}_{j}+\Delta q\left({\hat{b}}_{j}^{{\dagger}

}+{\hat{b}}_{j}\right){\hat{X}}_{j}^{{\dagger} }{\hat{X}}_{j}\right]\\\qquad\quad +\left({\hat{X}}_{j}^{{\dagger} }+{\hat{X}}_{j}\right)\left[{\Omega }_{+}\frac{{e}^{i{\omega

}_{+}t}}{2}+{\Omega }_{-}\frac{{e}^{i{\omega }_{-}t}}{2}+{g}_{0}{\hat{a}}^{{\dagger} }+\,{\mbox{H.c.}}\,\right].\end{array}$$ (1) We note that Δ_q_ parameterises the exciton-phonon coupling,

which takes the Holstein form32. This Holstein form may be developed from electron- and hole-phonon couplings and has been used to model TMD exciton lineshapes33,34. The Huang-Rhys

parameter _S_35, which is typically used to define coupling to phonons, is related to Δ_q_ by _S_ = Δ_q_2. Such coupling to vibrational modes is what leads to Raman scattering, so our

discussion is focused on Raman-active phonon modes. The terms \({\Omega }_{\pm }{e}^{i{\omega }_{\pm }t}\) denote the two driving fields. As discussed elsewhere4,36, two-frequency driving is

used to ensure resonance of both co- and counter-rotating couplings between photons and phonons, as illustrated in Fig. 1. That is, there are two processes we want to make resonant: The

process that destroys a photon and creates a phonon (the co-rotating process), and the process that creates both a photon and a phonon (the counter-rotating process). When using a single

pump frequency, the pump can be chosen to make one of these two-photon transitions resonant, but not both. Using two pumps allows for the simultaneous two-photon resonance of both processes.

As we will discuss further below, this simultaneous resonance can reduce the threshold power required by absorbing the phonon energy into the pumps’ difference frequency. In addition to the

Hamiltonian, we consider effects of dissipation by considering a Lindblad master equation37: \(i{\partial }_{t}\rho =[\hat{H},\rho ]+i{\sum }_{j}{{\mathcal{D}}}[{\hat{L}}_{j}]\), with

\({{\mathcal{D}}}[\hat{L}]=\hat{L}\rho {\hat{L}}^{{\dagger} }-\{{\hat{L}}^{{\dagger} }\hat{L},\rho \}/2\). We consider dissipation corresponding to cavity loss \({\hat{L}}_{c}=\sqrt{2\kappa

}\hat{a}\), exciton loss \({\hat{L}}_{{{\rm{ex}}},j}=\sqrt{{\Gamma }_{{{\rm{ex}}}}}{\hat{X}}_{j}\), and phonon loss \({\hat{L}}_{b,j}=\sqrt{{\Gamma }_{{{\rm{phon}}}}}{\hat{b}}_{j}\). The

symbol definitions and values used are included in Table 2. The cavity and pump frequencies are chosen to be close to that of the exciton, and so we move into a frame rotating at the mean

pump frequency \(\overline{\omega }\) and disregard counter-rotating terms. While these frequencies are close to resonance, we note that in the results shown below, we will work in a regime

where the two-photon process (i.e., the effective photon-phonon coupling) are closer to resonance than the one-photon process of exciton absorption. We choose this regime in order to keep

the exciton population and heating effects as small as possible. As noted above, the exciton population cannot necessarily be made sufficiently small to ignore, but keeping it as small as

attainable leads to a simpler picture. Following the rotating-wave approximation, we then implement a mean-field ansatz (details given in Methods) and obtain coupled equations for the

rescaled cavity field \(\alpha =\langle \hat{a}\rangle /\sqrt{N}\) and the density matrix of a single site _ρ_: $${\partial }_{t}\alpha =-i\left[-{\Delta }_{c}\alpha

+{g}_{0}\sqrt{N}\,{{\rm{Tr}}}\left(\rho \hat{X}\right)\right]-\kappa \alpha ;$$ (2) $${\partial }_{t}\rho =-i\left[{\hat{H}}_{{{\rm{mat}}}}^{{{\rm{MF}}}},\rho

\right]+{{\mathcal{D}}}\left[\sqrt{{\Gamma }_{{{\rm{ex}}}}}\hat{X}\right]+{{\mathcal{D}}}\left[\sqrt{{\Gamma }_{{{\rm{phon}}}}}\hat{b}\right].$$ (3) The mean-field material Hamiltonian

\({\hat{H}}_{{{\rm{mat}}}}^{{{\rm{MF}}}}\) is $$\begin{array}{l}{\hat{H}}_{{{\rm{mat}}}}^{{{\rm{MF}}}}=-{\Delta }_{{{\rm{ex}}}}{\hat{X}}^{{\dagger} }\hat{X}+{\omega

}_{{{\rm{phon}}}}\left[{\hat{b}}^{{\dagger} }\hat{b}+\Delta q\left(\hat{b}+{\hat{b}}^{{\dagger} }\right){\hat{X}}^{{\dagger} }\hat{X}\right]\\ +\left[\left({\Omega }_{+}\frac{{e}^{-i\Delta

\omega t}}{2}+{\Omega }_{-}\frac{{e}^{+i\Delta \omega t}}{2}+{g}_{0}\sqrt{N}\alpha \right){\hat{X}}^{{\dagger} }+\,{\mbox{H.c.}}\,\right],\end{array}$$ (4) where the detunings are given in

Table 1. The mean-field ansatz is appropriate in the limit we consider, where there is a very large number of emitters _N_ coupled to a single photon mode; mean-field theory has been proven

exact for open Dicke models in the limit of infinite _N_38. There remains explicit time dependence in the exciton drive at frequency Δ_ω_. As noted above, and can be seen in Fig. 1(b), this

detuning is included so that there can be resonant processes for scattering a phonon into a photon, as well as resonant processes to create a phonon-photon pair. Such resonance occurs if

Δphon ≡ Δ_ω_ − _ω_phon = 0. In most prior work on Raman-driving schemes, the exciton state would be eliminated, and the above resonant processes would then lead to an effective coupling of

the type \((\hat{a}+{\hat{a}}^{{\dagger} })({\hat{b}}_{j}+{\hat{b}}_{j}^{{\dagger} })\). This adiabatic elimination is not so clearly justified in this work, as we cannot necessarily operate

in a parameter regime where the exciton detuning is larger than all other detunings—we discuss relevant parameter values in the next subsection. In the following, we will solve this

periodically driven and dissipative mean-field model. We will first consider solutions with time dependence commensurate with the drive frequency; these are analogous to the steady-state

solutions found for a time-independent model. We will refer to such solutions as _stationary states_. As discussed further below, not all solutions take this form—analogous to limit cycles

in a time independent problem, one can also sometimes find solutions incommensurate with the drive frequency. When considering the stationary state, we can avoid needing to perform direct

time evolution of Eqs. (2) and (3), and can instead directly find the stationary states by looking for solutions in the form of a Fourier series: _α_(_t_) = ∑_n__α_ss,_n__e__i__n_Δ_ω__t_,

and _ρ_(_t_) = ∑_n__ρ_ss,_n__e__i__n_Δ_ω__t_, where the sum over _n_ is truncated at some maximum ∣_n_∣. See Methods for details on the solving process for the Fourier coefficients. Figure 2

shows that this procedure well matches the results of direct time evolution. This process can only find solutions analogous to steady states of a time-independent driven system; direct time

evolution must be used to find analogues to limit cycles, which may have time scales far longer than the periodic driving. The stationary-state solver always finds a normal state with

_α_ss,0 = 0, i.e., one with zero steady population of the cavity. However, because the pumps are still interacting with excitons and excitons continue to scatter into the cavity, the

nonzero-frequency components of _α_ss in the normal state do not vanish—specifically terms with odd _n_ are nonzero, as seen in Fig. 2. While this normal state always exists, it is not

always stable. To determine this, we linearise the master equation about one of its stationary states. This results in an equation in Floquet form. The Floquet exponents found from this

equation then determine the stability of the stationary state: If any Floquet exponent has real part greater than zero, then the state is unstable. For our time-dependent system, these

Floquet exponents play the role that linear-stability eigenvalues played in previous work39. We therefore refer to these Floquet exponents as eigenvalues in what follows; see Methods for

further details. Regimes where the normal state with _α_ss,0 = 0 is stable we term the _normal phase_. Regimes where the normal state is unstable are discussed below, as we find multiple

other states that may arise. LOW-ENERGY EFFECTIVE MODEL Before presenting results found directly from the stationary state and stability analysis of the full photon-exciton-phonon model

discussed in the previous section, we introduce an effective model that provides a qualitative understanding of the results. This effective model results from adiabatic elimination of the

exciton states, leading to an effective photon-phonon model, as discussed in the Supplementary Information40. It takes the form \({\hat{H}}_{{{\rm{eff}}}}=-{\Delta

}_{c}^{D}{\hat{a}}^{{\dagger} }\hat{a}+\mathop{\sum }_{j = 1}^{N}{\hat{H}}_{{{\rm{eff}}},j}\), with $${\hat{H}}_{{{\rm{eff}}},j}=\mathop{\sum }_{j=1}^{N}-{\Delta

}_{{{\rm{phon}}}}{\hat{b}}_{j}^{{\dagger} }{\hat{b}}_{j}+\left({\lambda }_{+}\hat{a}{\hat{b}}_{j}+{\lambda }_{-}\hat{a}{\hat{b}}_{j}^{{\dagger} }+\,{\mbox{H.c.}}\,\right).$$ (5) This

effective model is similar to the generalised Dicke model4, with distinct co- and counter-rotating couplings (_λ_∓, respectively). However, the effective model in Eq. (5) differs from the

Dicke model in that it replaces two-level systems by bosons (phonons); this would change the behaviour of such a model above threshold, but does not modify the location of the threshold. The

phase diagram of the generalised Dicke model has been studied in several places41,42,43,44,45. We will refer to these works, particularly42, to interpret features of the phase diagrams we

find in the following. We can derive approximate perturbative forms for the couplings _λ_± and the dressed-cavity detuning \({\Delta }_{c}^{D}\) appearing in this model in the limit where

the phonon energy _ω_phon is close to Δ_ω_ and all detunings are much smaller than this scale: i.e., for \({\Delta }_{{{\rm{ex}}}}^{D},{\Delta }_{c},{\Delta }_{{{\rm{phon}}}}\ll {\omega

}_{{{\rm{phon}}}}\approx \Delta \omega\). Here we have introduced the dressed exciton detuning \({\Delta }_{{{\rm{ex}}}}^{D}={\Delta }_{{{\rm{ex}}}}+{\omega }_{{{\rm{phon}}}}\Delta

{q}^{2}\), accounting for polaron dressing of the exciton. That is, \({\Delta }_{{{\rm{ex}}}}^{D}\) corresponds to detuning between the pump and the polaron energy, where the polaron energy

is the lowest energy attainable in the one-exciton manifold, corresponding to minimising the Hamiltonian \({\omega }_{{{\rm{phon}}}}[{\hat{b}}^{{\dagger} }\hat{b}+\Delta

q({\hat{b}}^{{\dagger} }+\hat{b}){\hat{X}}^{{\dagger} }\hat{X}]\). In the limit where all detunings are much smaller than _ω_phon, we find: $${\lambda }_{\pm }=\frac{1}{4}{\Omega }_{\pm

}{g}_{0}\Delta q\left(\frac{1}{{\Delta }_{{{\rm{ex}}}}^{D}\pm {\Delta }_{{{\rm{phon}}}}}+\frac{1}{{\Delta }_{{{\rm{ex}}}}^{D}-{\Delta }_{c}}\right),$$ (6) along with \({\Delta

}_{c}^{D}={\Delta }_{c}+{g}_{0}^{2}N/\left({\Delta }_{{{\rm{ex}}}}^{D}-{\Delta }_{c}\right)\). This dressed cavity detuning accounts for hybridisation of photons with excitons. As well as

modifying this detuning, this hybridisation also modifies loss terms, so that cavity loss is increased: \(\kappa \to {\kappa }^{D}=\kappa +\frac{1}{2}{g}_{0}^{2}N{\Gamma

}_{{{\rm{ex}}}}/{\left({\Delta }_{{{\rm{ex}}}}^{D}-{\Delta }_{c}\right)}^{2}\). In40, we provide an alternative numerical approach to give non-perturbative estimates of these dressed

energies and decay rates. While the model above does not provide quantitatively accurate results, it does indicate what conditions might favour strong coupling between phonons and photons,

and thus photon-polariton condensation. From the form of Eq. (6), there are two possible conditions that lead to large values of _λ_±, corresponding to either of the two denominators

approaching zero. These two cases correspond to the exciton being in resonance with the cavity, or to a vibrational sideband of the exciton being in resonance with one of the pumps. In both

cases, this can lead to a large population of excitons, thus invalidating the adiabatic elimination, and furthermore causing heating due to exciton decay. The ideal scenario is to be very

close to the two-photon resonance (i.e., where the Raman process resonantly creates or destroys a phonon), while avoiding the one-photon resonance that leads to large exciton populations. We

also note that Eq. (6) suggests that the denominators can be made arbitrarily small, leading to arbitrarily large coupling. However, exciton and phonon decay rates introduce cutoffs on

these denominators. This consideration motivates the values of the control parameters Δex, Δ_c_, Δphon used in this work, in that we generally probe the regimes \(\left\vert {\Delta

}_{{{\rm{ex}}}}^{D}\right\vert \gtrsim {\Gamma }_{{{\rm{ex}}}}\) and \(\left\vert {\Delta }_{{{\rm{phon}}}}\right\vert \gtrsim {\Gamma }_{{{\rm{phon}}}}\). SUPERRADIANT PHASE TRANSITION

Considering the full photon-exciton-phonon model of Sec. II A, we next discuss the ways in which the system may transition into a superradiant state (i.e., to a phonon-polariton condensate).

As discussed above, the _α_ss,0 = 0 stationary state may go from stable to unstable as indicated by the eigenvalues of the Floquet problem. Such instability can arise as one increases the

driving strength. We discuss here two scenarios of what may happen at this instability, associated with continuous and discontinuous phase transitions. In the continuous case, the

instability of the normal state coincides with the appearance of a new stable stationary state in which _α_ss,0 ≠ 0. Such states correspond to a macroscopic population of the cavity that

spontaneously breaks the symmetry of the model. In the original frame, _α_ss,0 corresponds to cavity light at the mean pump frequency \(\overline{\omega }\): The appearance of light at this

mean frequency is understood as the signature of a superradiant state4,36. Stationary states with _α_ss,0 ≠ 0 must come in equal and opposite pairs in the complex plane because the master

equation has a (weak46,47) symmetry under the transformation \((\alpha ,\hat{X})\leftrightarrow (-\alpha ,-\hat{X})\). As such, the appearance of nonzero _α_ss,0 corresponds to spontaneous

symmetry breaking. An illustration of this scenario is shown in Fig. 3. Zooming in near the transition, we see it occurs when a single, real eigenvalue goes from negative to positive,

corresponding to a pitchfork-bifurcation instability48. This corresponds to the standard continuous phase transition to the Hepp-Lieb-Dicke superradiant phase8. The critical pumping strength

may be estimated using the low-energy effective model introduced above. For effective couplings that are nearly equal, \(\left\vert {\lambda }_{-}-{\lambda }_{+}\right\vert \ll {\lambda

}_{-}+{\lambda }_{+}\), the transition occurs when8 $${\lambda }_{-}{\lambda }_{+}N=\frac{1}{4}\left(\frac{{({\Delta }_{c}^{D})}^{2}+{({\kappa }^{D})}^{2}}{{\Delta

}_{c}^{D}}\right)\left(\frac{{\Delta }_{{{\rm{phon}}}}^{2}+{\Gamma }_{{{\rm{phon}}}}^{2}/4}{{\Delta }_{{{\rm{phon}}}}}\right).$$ (7) The right-hand side of this expression reduces to the

more familiar \({\Delta }_{c}^{D}{\Delta }_{{{\rm{phon}}}}/4\) if loss is ignored. However, including effects of loss is crucial for understanding the minimal threshold pump power

attainable, as we discuss further in Sec. II E. A notable feature of the low-energy effective model is the replacement of bare cavity loss by the effective loss rate _κ__D_. This effect can

be seen directly from Fig. 3b. The intercepts of each line with the vertical axis indicate the linewidths of the effective modes in the absence of pumping, i.e., when _λ_± = 0. One may see

that the darkest line, corresponding to the cavity mode, has an intercept much below − _κ_, where _κ_ = 6 × 10−4 meV. We previously gave the perturbative expression for the dressed linewidth

as \({\kappa }^{D}=\kappa +\frac{1}{2}{g}_{0}^{2}N{\Gamma }_{{{\rm{ex}}}}/{\left({\Delta }_{{{\rm{ex}}}}^{D}-{\Delta }_{c}\right)}^{2}\). For the parameters of Fig. 3(b), this yields _κ__D_

≈ 0.009 meV, while the intercept in the plot is −0.004 meV. The discrepancy is due to the large value of the parameter that controls the perturbation expansion,

\({g}_{0}\sqrt{N}/\left({\Delta }_{{{\rm{ex}}}}^{D}-{\Delta }_{c}\right)\approx 0.5\). One may note that the expansion overestimates the broadening because it disregards the eventual

saturation of the dressed cavity linewidth at very large coupling \({g}_{0}\sqrt{N}\): In the large-coupling limit, the relevant mode becomes an equal superposition of cavity and exciton,

with a corresponding linewidth \({\kappa }^{D}=\frac{1}{2}\kappa +\frac{1}{4}{\Gamma }_{{{\rm{ex}}}}\). In other parameter regimes, the transition to the superradiant state can be

discontinuous. An example of this is shown in Fig. 4, where a stable superradiant state emerges from a saddle-node bifurcation at nonzero _α_ss,0 at a particular driving strength Ω. There is

a range of driving strengths above this for which the mean-field theory predicts bistability. At the upper limit of the bistable region, the normal phase goes unstable at a subcritical

rather than a supercritical pitchfork bifurcation48. This case allows for hysteresis, and it illustrates an unusual first-order superradiant transition49,50; as with other models where

mean-field theory supports bistability, beyond-mean-field treatments are expected to predict a unique discontinuous phase transition, determined by the switching rates between the _α_ss,0 =

0 and _α_ss,0 ≠ 0 solutions. Although this transition is discontinuous, we note it still involves spontaneous symmetry breaking to pick the sign of _α_ss,0. In addition to exhibiting a

discontinuous transition, Fig. 4 also shows another notable feature: A transition back to the normal state at larger pump strengths. Similar behaviour has been discussed in other lasing or

superradiance models, e.g.,51—strong pumping can cause an increase of effective linewidth, i.e., a form of power broadening52. We note that such an effect is often lacking in approaches that

have adiabatically eliminated intermediate states involved in the pumping. LASING TRANSITION The emergence of a superradiant state is not the only manner in which the normal phase can go

unstable. There is also a scenario where two complex-conjugate eigenvalues simultaneously cross the imaginary axis. This corresponds to a Hopf bifurcation48 and is expected to lead to a

limit cycle. Indeed, as seen in Fig. 5, we find that in this case the cavity amplitude _α_ spirals out from the origin and undergoes large-scale oscillations on a timescale that is much

longer than the period of the drive, 1/Δ_ω_. That is, the time dependence of this solution is not commensurate with the drive. Near to the transition, the frequency of these slow

oscillations matches the imaginary part of eigenvalue, as is typical for a Hopf bifurcation. Because the stationary-state solver assumes that the final frequency components are integer

multiples of Δ_ω_, it cannot find these incommensurate solutions. As such, we use direct integration of the master equation to check the stability of the limit cycle. We denote this

behaviour the _lasing_ phase, in analogy to the phases found in the generalised Dicke model. After adiabatic elimination of excitons, the generalised Dicke model (as found in Sec. II B) is

time-independent in the frame of the average pump frequency. One can distinguish time-independent (superradiant) and time-dependent (lasing) states in such a case. Reference42 showed that

there are two different parameter regimes where the generalised Dicke model exhibits lasing. The first is the typical lasing regime, where an incoherent drive leads to inversion of the

emitters, causing gain for the cavity mode. However, the model of Sec. II B has no incoherent drive, only decay, and the emitters in Eq. (6) are bosons, not two-level systems. As such,

inversion of emitters is not relevant for the case we consider here. The second lasing state has a different character. This state is found either when _λ_+ ≫ _λ_−, or when the sum of the

cavity and emitter frequencies approach zero. In either of these cases, the dominant matter-light coupling is one that creates a photon and _excites_ an emitter, the counter-rotating

coupling. This then leads to a state that has been referred to as “counter-lasing”44,45. In the case shown in Fig. 5 (and also discussed further below), our time-dependent phase can be

ascribed to counter-lasing driven by near-resonance of the process that creates a photon and excites an emitter; see, e.g., Fig. 8 of Ref. 42. Such resonance would occur if \({\Delta

}_{c}^{D}=-{\Delta }_{{{\rm{phon}}}}\). Even though the bare detuning Δ_c_ is negative in Fig. 5, corresponding to red detuning, the shift due to the exciton-cavity coupling can push

\({\Delta }_{c}^{D}\) to become positive, corresponding to effective blue detuning. In principle, counter-lasing may also occur in our model due to _λ_+ ≫ _λ_−, but this requires larger

Δphon and takes the system out of the small-detuning regime used to derive _λ_±. PHASE DIAGRAM Having discussed the forms of instability that can arise, we now discuss the phase diagram,

indicating which forms of instability occur for certain parameters. A key practical question is what critical pump strength is required to reach either the superradiant or lasing

instability. Figure 6 shows this diagram, mapping out the critical pump strength at which the normal phase goes unstable due to a single eigenvalue (superradiant state) or a pair of

complex-conjugate eigenvalues (lasing). Dark shading indicates where a transition can occur at low pump power. White regions indicate parameters for which no instability of the normal state

is found. Experimentally exploring this full phase diagram requires tuning both the mean pump frequency \(\overline{\omega }\) and the cavity frequency. Changing only the mean pump frequency

corresponds to diagonal traces through this figure from lower left to upper right. The superradiant and lasing phases appear continuously connected in the space of Δ_c_ and Δex in some

regimes, but for other regimes they are separated. Details of this structure can be seen in the cross section in Fig. 6(b). A jump in the critical pump strength within the superradiant phase

is also exhibited. This is associated with switching between the continuous and discontinuous phase transitions. To see how this scenario evolves in more detail, Supplementary Note 240

shows how eigenvalues coming close to but not crossing the imaginary axis can result in jumps in the transition pumping strength. A notable feature of this figure is the change in behaviour

as the exciton detuning Δex is tuned through − _ω_phonΔ_q_2 as indicated by the dotted line. This corresponds to \({\Delta }_{{{\rm{ex}}}}^{D}\) crossing zero, or equivalently, to tuning the

mean pump frequency through the polaron energy. At this detuning we see a narrow sliver of superradiant state. One may note that the low-energy effective model does not apply under this

condition because resonance results in stationary states that have high-exciton population even at low pump strength. A second consequence of small \({\Delta }_{{{\rm{ex}}}}^{D}\) is a very

large shift to the dressed photon frequency; i.e., \({\Delta }_{c}^{D}\) is large and positive just below \({\Delta }_{{{\rm{ex}}}}^{D}=0\), and large and negative just above this line. This

in turn explains why the superradiant state ceases for Δex > − _ω_phonΔ_q_2. A second important feature occurs when \({\Delta }_{c}^{D}\) changes sign, as shown by the dashed curves in

Fig. 6. As discussed in the previous section, counter-lasing occurs in general for positive \({\Delta }_{c}^{D}\), and in particular when \({\Delta }_{c}^{D}\simeq -{\Delta

}_{{{\rm{phon}}}}\). In contrast, the superradiant state occurs for negative \({\Delta }_{c}^{D}\). Since Fig. 6 is plotted at fixed Δ_ω_ and thus fixed Δphon, the switch from the

superradiant phase to counter-lasing is driven by changing \({\Delta }_{c}^{D}\). As can be understood from the low-energy effective model (i.e., Eq. (6) and Eq. (7)), the points of

particularly low threshold are close to points where the transition ceases to exist. This corresponds to the standard observation that with dissipation, the lowest threshold occurs when

\({\Delta }_{c}^{D}={\kappa }^{D}\), while the transition vanishes at \({\Delta }_{c}^{D}=0\). In Fig. 6(a), the dashed line corresponding to \({\Delta }_{c}^{D}=0\) does not exactly match

the point where the superradiant transition ceases; this is because the estimate of \({\Delta }_{c}^{D}\) used here neglects effects of the AC Stark shift of the exciton due to the finite

pump strength _Ω_±. In contrast, calculations in Ref. 40 performed for the low-energy effective model (i.e., neglecting this AC Stark shift) do show the expected agreement. DISCUSSION In the

results above we have shown that, considering a standard model of Holstein coupling between excitons and phonons, one can realise a Raman-driving scheme to couple Raman-active phonons to

light. One can thus realise a phonon-polariton condensate that is indicated by a steep jump in cavity photon emission. Furthermore, below threshold all emitted light is at the frequencies of

the pumps; above threshold, light will come out at the average of these frequencies (superradiant phase) or at an incommensurate frequency (lasing phase). The corresponding changes to the

phonon mode frequencies can be further verified with in situ Raman spectroscopy. While an effective model that adiabatically eliminates the excitons can qualitatively describe the phases, we

found that this adiabatic elimination is not quantitatively accurate for the chosen parameters relevant to TMDs. In principle, for materials with very large band gaps and thus large exciton

energies, such adiabatic elimination may be adequate. However, for the materials we consider, one must use a more sophisticated method that retains the exciton states and thus requires a

treatment of a periodically driven system. Our results are written in terms of the driving strength _Ω_± appearing in Eq. (1). Here we discuss the practicality of attaining these values in

terms of required laser power. We also discuss design principles for choices of materials as well as open questions arising from this work. To estimate the laser power required to reach the

superradiant transition, we make several simplifications to obtain a closed-form expression. First, we set the detunings \({\Delta }_{{{\rm{ex}}}}^{D}\) and Δphon to half the exciton and

phonon linewidths, respectively. Second, we assume we work in the regime of large exciton-cavity coupling; in this regime, as discussed above, the dressed-cavity linewidth _κ__D_ ≃ _Γ_ex/4,

a linear scaling with exciton linewidth. (We discuss the other possible regimes in Ref. 40.) Third, we set the denominators in the effective couplings Eq. (6) to _Γ_ex because \({\Delta

}_{{{\rm{ex}}}}^{D}\) is the largest energy scale in the denominators and is assumed to be dressed by exciton decay of an amount between \(\frac{1}{2}{\Gamma }_{{{\rm{ex}}}}\) and _Γ_ex.

Finally, we choose equal pumping, so Ω± = Ω. With these choices, the threshold condition becomes \({\left({\Omega }_{{{\rm{crit}}}}{g}_{0}\Delta q\right)}^{2}N=\frac{1}{2}{\Gamma

}_{{{\rm{ex}}}}^{3}{\Gamma }_{{{\rm{phon}}}}\). To convert this from a critical value of Ω to a critical laser power, we must relate the light-matter coupling parameters in our model to

electric field strengths of the cavity and pump light. The exciton-light couplings can be written as \(\Omega \sqrt{N}={e}_{{{\rm{ex}}}}\sqrt{A}{E}_{p}\) and

\({g}_{0}\sqrt{N}={e}_{{{\rm{ex}}}}\sqrt{A}{E}_{c}\) for pump and cavity electric fields _E__p_,_c_, material area _A_, and exciton matrix element _e_ex; see53 and40 for details. We write

the number of emitters as _N_ = _n__A_ for emitter density _n_. Assuming the pump is a Gaussian beam impinging onto the material area, its power is \(P=\frac{1}{4}{\varepsilon

}_{0}{E}_{p}^{2}Ac\). The threshold pump power is then: $${P}_{{{\rm{crit}}}}=\frac{{\Gamma }_{{{\rm{ex}}}}^{3}{\Gamma }_{{{\rm{phon}}}}n{\varepsilon }_{0}c}{8{e}_{{{\rm{ex}}}}^{4}\Delta

{q}^{2}{E}_{c}^{2}}.$$ (8) We see from this expression that the critical pump power depends separately on the density of emitters _n_ and the matrix element _e_ex, and not just upon the

combination \({e}_{{{\rm{ex}}}}/\sqrt{n}\) that controls the coupling strength _g_0. Since the materials we wish to consider do not actually consist of a set of localised emitters, a choice

must be made to give separate estimates of _n_ and _e_ex. In the following we will set the emitter density to the inverse unit cell area—alternative choices are the Mott density and inverse

exciton area54. We take MoSe2 as our model material, so we set _Γ_ex = 1 meV, _Γ_phon = 0.05 meV, _e_ex = 0.23_e_, Δ_q_2 = 1, and \({n}^{-1}=\sqrt{3}{a}_{0}^{2}/2\) for a lattice spacing of

_a_0 = 3.3 Å26,29,30,53. We set the cavity waist to _w_0 = 30 μm and quantise its electric field over cavity length _L_ = 1 cm with a Gaussian mode profile; note that a cavity this long

allows for transverse pumping and cryogenic cooling of a sample in situ. This yields a threshold pump power of _P_crit = 30 W. While this is too great to be immediately feasible, we will

remark later on how a multimode cavity may bring this down to a practical regime. Note that the dependence of the critical power on \({e}_{{{\rm{ex}}}}^{4}\) and \({\Gamma

}_{{{\rm{ex}}}}^{3}\) mean small changes in estimates of these parameters have large effects on the critical power. As mentioned before, the model we discuss is not specific to TMDs and can

be applied to other materials. This prompts the question of which material properties would be best-suited to realising phonon-polariton condensation. Based on the results above, an estimate

of this can be found by considering how to maximise the effective coupling defined in Eq. (6) or minimise the threshold power of Eq. (8). These expressions highlight the beneficial effects

of the exciton matrix element and the Huang-Rhys parameter _S_ = Δ_q_2 defining the exciton-phonon coupling, as well as the adverse effect of the exciton linewidth. To conclude this

discussion, we briefly mention some topics that could be addressed in future work. MULTIMODE CAVITIES This paper considers a single-mode cavity for simplicity, but experiments using a

degenerate confocal cavity9 have been realised for ultracold atoms. In such confocal cavities, one can obtain a field enhancement10,55 by constructive interference between different

degenerate modes building a synthetic cavity mode localised to have perfect overlap with the cloud of atoms. Such an approach can also be used in this solid-state context to maximise overlap

with whichever is smaller, the sample or the pump spot. Such an approach thus allows one to further enhance the cavity-exciton coupling. In particular, a multimode cavity may reduce the

threshold laser power required. To continue the calculation from before, if one considers a pump beam waist of _w__p_ = 5 μm, then the confocal enhancement would be

\({({w}_{0}/{w}_{p})}^{2}=36\), reducing the critical pump threshold to below 1 W. A more sophisticated treatment of multiple cavity modes may however need to go beyond the mean-field

ansatz. Mean-field approaches may remain valid when the number of emitters is larger than the number of relevant cavity modes56; exploring this question is the subject of future work.

TEMPERATURE In our calculations above, we implicitly assumed a low-temperature state, in which there is no population of phonons in the initial state. Such an approach is reasonable when

considering experiments at cryogenic temperatures, i.e., when the temperature is much smaller than the phonon energy. Cryogenic cooling to this low-temperature state should also allow one to

minimise heating effects from the continuous-wave pumping. Extending the calculations here to consider materials at higher temperature (e.g., room temperature) is an open question. In

particular, at higher temperatures it may be important to distinguish between the exciton and phonon linewidths due to decay versus dephasing. As has been explored in simple models42,

dephasing and decay have different effects on the threshold for condensation. EFFECTS ON ELECTRONIC STATES A key question for future work is to assess the effect of phonon polariton

condensation on electronic and transport properties, following methods such as those in Refs. 2,3,20. A related question is to explore whether other states can be realised by the Raman

pumping scheme in this work, such as more complex limit cycles or chaotic phases. METHODS TRANSFORMATION TO MEAN-FIELD HAMILTONIAN To transform the original Hamiltonian, Eq. (1), into the

frame rotating at \(\overline{\omega }\), we use the unitary transform: $${\hat{U}}_{{{\rm{rot}}}}=\exp \left[i\overline{\omega }t\left({\hat{a}}^{{\dagger}

}\hat{a}+\sum\limits_{j=1}^{N}{\hat{X}}_{j}^{{\dagger} }{\hat{X}}_{j}\right)\right].$$ (9) To derive the model in Eqs. (2)–(4), we then disregard terms rotating at \(2\overline{\omega }\)

and \(\overline{\omega }+{\omega }_{\pm }\). We then make a mean-field approximation, equivalent to assuming the density matrix factorises into terms for the cavity and for each site. With

this approximation, the equation of motion for the cavity becomes that of a coherently driven damped harmonic oscillator, and so its behaviour is captured by considering the evolution of the

coherent state amplitude: $$\alpha \equiv \frac{\langle \hat{a}\rangle }{\sqrt{N}}.$$ (10) For the matter component, we assume all sites are equivalent, leading to the site-independent

model in Eq. (4). FOURIER ANALYSIS AND LINEAR STABILITY The Fourier series ansatz for stationary states transforms the system of nonlinear differential equations for (_α_, _ρ_) into a system

of nonlinear algebraic equations for \(({\alpha }_{{{\rm{ss}}},n},{\rho }_{{{\rm{ss}}},n})\). All nonlinearity here arises from the dependence on _α_ss,_n_. As such, at fixed _α_ss,_n_, the

problem simplifies into a linear homogeneous system for _ρ_ss,_n_. The trace constraint \({{\rm{Tr}}}({\rho }_{{{\rm{ss}}},n\ne 0})=0\) is already enforced by the system, but we must

manually add the normalisation constraint \({{\rm{Tr}}}({\rho }_{{{\rm{ss}}},0})=1\) to one of the rows. We then solve this exactly determined system for _ρ_ss,_n_ via sparse LU

factorisation, and we feed the result back into the objective function for _α_ss,_n_. This reduces the size of the nonlinear system from the full space of \(({\alpha }_{{{\rm{ss}}},n},{\rho

}_{{{\rm{ss}}},n})\) to the 2_M_ + 1 complex numbers _α_ss,_n_, where _M_ is the maximum ∣_n_∣ retained in the sum; i.e., _M_ is the cutoff on Fourier components. We also find the Jacobian

of the objective function of _α_ss,_n_ to accelerate the nonlinear root-finding. The Fourier cutoff _M_ is typically set to 4, but it is occasionally set to 6 for detailed comparison to time

evolution, as indicated in Fig. 4 and Table 2. We use the default settings in both the sparse LU factorisation and the root-finding using the Levenberg-Marquardt algorithm57,58, as

implemented in SciPy59 following MINPACK60. The stationary-state solver returns a solution \(\left({\alpha }_{{{\rm{ss}}}}(t),{\rho }_{{{\rm{ss}}}}(t)\right)\) with period _T_ = 2_π_/Δ_ω_.

To determine linear stability, we assume a small fluctuation about this stationary state: _α_(_t_) = _α_ss(_t_) + _δ__α_(_t_) and _ρ_(_t_) = _ρ_ss(_t_) + _δ__ρ_(_t_), from which we obtain a

system of differential equations for \(\left(\delta \alpha (t),\delta \rho (t)\right)\) that is linear but with explicit, periodic time dependence. Writing this system as \({\partial

}_{t}\vec{x}=\hat{A}(t)\vec{x}\) for \(\vec{x}=(\delta \alpha ,\delta \rho )\) and _T_-periodic \(\hat{A}(t)\), we integrate to find the one-period evolution operator, also termed the

monodromy matrix61: $$\hat{{{\mathcal{M}}}}={{{\rm{T}}}}_{\leftarrow }\exp \left[\int_{0}^{T}\hat{A}(t)\,dt\right],$$ (11) where T← is the time-ordering symbol. We perform this integral by

exponentiating and multiplying over discrete time steps of size _T_/100; we find this faster and more stable than any more sophisticated methods. The slow step is the subsequent

diagonalisation of \(\hat{{{\mathcal{M}}}}\), yielding eigenvalues \({e}^{{\mu }_{k}T}\) for Floquet multipliers _μ__k_. As mentioned before, these _μ__k_ are called eigenvalues in this

manuscript. Direct time evolution of the system is performed using Netlib’s zvode, as implemented in SciPy59. We use the implicit Adams method at order 12, with rtol and atol parameters of

10−9 and 10−12, respectively, and with a maximum number of steps of 1000. Table 2 provides a summary of parameter values used in our numerical calculations. Throughout, QuTiP62 is used to

create sparse matrices and to interpret density matrices, though the mean-field setup is not directly amenable to QuTiP methods. DATA AVAILABILITY The data that support the findings of this

study are available in the Harvard Dataverse Repository, https://doi.org/10.7910/DVN/YGHFH2. CODE AVAILABILITY The code used for the current study is available in the Harvard Dataverse

Repository, https://doi.org/10.7910/DVN/YGHFH2. REFERENCES * Basov, D. N., Asenjo-Garcia, A., Schuck, P. J., Zhu, X. & Rubio, A. Polariton panorama. _Nanophotonics_ 10, 549 (2020).

Article  Google Scholar  * Sentef, M. A., Ruggenthaler, M. & Rubio, A. Cavity quantum-electrodynamical polaritonically enhanced electron-phonon coupling and its influence on

superconductivity. _Sci. Adv._ 4, eaau6969 (2018). Article  ADS  Google Scholar  * Mankowsky, R. et al. Nonlinear lattice dynamics as a basis for enhanced superconductivity in YBa2Cu3O6.5.

_Nature_ 516, 71 (2014). Article  ADS  Google Scholar  * Dimer, F., Estienne, B., Parkins, A. S. & Carmichael, H. J. Proposed realization of the Dicke-model quantum phase transition in

an optical cavity QED system. _Phys. Rev. A_ 75, 013804 (2007). Article  ADS  Google Scholar  * Baumann, K., Guerlin, C., Brennecke, F. & Esslinger, T. Dicke quantum phase transition

with a superfluid gas in an optical cavity. _Nature_ 464, 1301 (2010). Article  ADS  Google Scholar  * Hepp, K. & Lieb, E. H. On the superradiant phase transition for molecules in a

quantized radiation field: the dicke maser model. _Ann. Phys._ 76, 360 (1973). Article  ADS  MathSciNet  Google Scholar  * Wang, Y. K. & Hioe, F. T. Phase Transition in the Dicke Model

of Superradiance. _Phys. Rev. A_ 7, 831 (1973). Article  ADS  Google Scholar  * Kirton, P., Roses, M. M., Keeling, J. & Dalla Torre, E. G. Introduction to the Dicke Model: From

Equilibrium to Nonequilibrium, and Vice Versa. _Adv. Quantum Technol._ 2, 1800043 (2019). Article  Google Scholar  * Kollár, A. J., Papageorge, A. T., Baumann, K., Armen, M. A. & Lev, B.

L. An adjustable-length cavity and Bose-Einstein condensate apparatus for multimode cavity QED. _N. J. Phys._ 17, 043012 (2015). Article  Google Scholar  * Vaidya, V. D. et al.

Tunable-Range, Photon-Mediated Atomic Interactions in Multimode Cavity QED. _Phys. Rev. X_ 8, 011002 (2018). Google Scholar  * Guo, Y., Kroeze, R. M., Vaidya, V. D., Keeling, J. & Lev,

B. L. Sign-Changing Photon-Mediated Atom Interactions in Multimode Cavity Quantum Electrodynamics. _Phys. Rev. Lett._ 122, 193601 (2019). Article  ADS  Google Scholar  * Guo, Y. et al. An

optical lattice with sound. _Nature_ 599, 211 (2021). Article  ADS  Google Scholar  * Kroeze, R. M. et al. Replica symmetry breaking in a quantum-optical vector spin glass,

http://arxiv.org/abs/arXiv:2311.04216 (2023). * Ritsch, H., Domokos, P., Brennecke, F. & Esslinger, T. Cold atoms in cavity-generated dynamical optical potentials. _Rev. Mod. Phys._ 85,

553 (2013). Article  ADS  Google Scholar  * Mivehvar, F., Piazza, F., Donner, T. & Ritsch, H. Cavity QED with quantum gases: new paradigms in many-body physics. _Adv. Phys._ 70, 1

(2021). Article  ADS  Google Scholar  * Fausti, D. et al. Light-Induced Superconductivity in a Stripe-Ordered Cuprate. _Science_ 331, 189 (2011). Article  ADS  Google Scholar  * Mitrano, M.

et al. Possible light-induced superconductivity in K3C60 at high temperature. _Nature_ 530, 461 (2016). Article  ADS  Google Scholar  * Cavalleri, A. Photo-induced superconductivity.

_Contemp. Phys._ 59, 31 (2017). Article  ADS  Google Scholar  * Curtis, J. B. et al. Cavity magnon-polaritons in cuprate parent compounds. _Phys. Rev. Res._ 4, 013101 (2022). Article  Google

Scholar  * Schlawin, F., Kennes, D. M. & Sentef, M. A. Cavity quantum materials. _Appl. Phys. Rev._ 9, 011312 (2022). Article  ADS  Google Scholar  * Schlawin, F., Cavalleri, A. &

Jaksch, D. Cavity-Mediated Electron-Photon Superconductivity. _Phys. Rev. Lett._ 122, 133602 (2019). Article  ADS  Google Scholar  * Curtis, J. B., Raines, Z. M., Allocca, A. A., Hafezi, M.

& Galitski, V. M. Cavity Quantum Eliashberg Enhancement of Superconductivity. _Phys. Rev. Lett._ 122, 167002 (2019). Article  ADS  Google Scholar  * Gao, H., Schlawin, F., Buzzi, M.,

Cavalleri, A. & Jaksch, D. Photoinduced Electron Pairing in a Driven Cavity. _Phys. Rev. Lett._ 125, 053602 (2020). Article  ADS  Google Scholar  * Collado, H. P. O., Michael, M. H.,

Skulte, J., Rubio, A. and Mathey, L. Equilibrium parametric amplification in Raman-cavity hybrids, (2023), arXiv:2312.14243 * Koppens, F. H. L. et al. Photodetectors based on graphene, other

two-dimensional materials and hybrid systems. _Nat. Nanotech_ 9, 780 (2014). Article  ADS  Google Scholar  * Cadiz, F. et al. Excitonic Linewidth Approaching the Homogeneous Limit in

MoS2-Based van der Waals Heterostructures. _Phys. Rev. X_ 7, 021026 (2017). Google Scholar  * Li, Y. et al. Measurement of the optical dielectric function of monolayer transition-metal

dichalcogenides: MoS2, MoSe2, WS2, and WSe2. _Phys. Rev. B_ 90, 205422 (2014). Article  ADS  Google Scholar  * Wang, G. et al. _Colloquium_: Excitons in atomically thin transition metal

dichalcogenides. _Rev. Mod. Phys._ 90, 021001 (2018). Article  ADS  MathSciNet  Google Scholar  * Li, D. et al. Exciton-phonon coupling strength in single-layer MoSe2 at room temperature.

_Nat. Commun._ 12, 954 (2021). Article  ADS  Google Scholar  * Kumar, D., Kumar, V., Kumar, R., Kumar, M. & Kumar, P. Electron-phonon coupling, thermal expansion coefficient, resonance

effect, and phonon dynamics in high-quality CVD-grown monolayer and bilayer MoSe 2. _Phys. Rev. B_ 105, 085419 (2022). Article  ADS  Google Scholar  * Molina-Sánchez, A. & Wirtz, L.

Phonons in single-layer and few-layer MoS2 and WS2. _Phys. Rev. B_ 84, 155413 (2011). Article  ADS  Google Scholar  * Holstein, T. Studies of polaron motion. _Ann. Phys._ 8, 325 (1959).

Article  ADS  Google Scholar  * Selig, M. et al. Excitonic linewidth and coherence lifetime in monolayer transition metal dichalcogenides. _Nat. Commun._ 7, 13279 (2016). Article  ADS 

Google Scholar  * Christiansen, D. et al. Phonon Sidebands in Monolayer Transition Metal Dichalcogenides. _Phys. Rev. Lett._ 119, 187402 (2017). Article  ADS  Google Scholar  * Huang, K.

& Rhys, A. Theory of light absorption and non-radiative transitions in _F_-centres. _Proc. R. Soc. Lond. A_ 204, 406 (1950). Article  ADS  Google Scholar  * Kroeze, R. M., Guo, Y.,

Vaidya, V. D., Keeling, J. & Lev, B. L. Spinor Self-Ordering of a Quantum Gas in a Cavity. _Phys. Rev. Lett._ 121, 163601 (2018). Article  ADS  Google Scholar  * Breuer, H.-P. and

Petruccione, F., _The Theory of Open Quantum Systems_https://doi.org/10.1093/acprof:oso/9780199213900.001.0001 (Oxford University Press, 2007). * Carollo, F. & Lesanovsky, I. Exactness

of Mean-Field Equations for Open Dicke Models with an Application to Pattern Retrieval Dynamics. _Phys. Rev. Lett._ 126, 230601 (2021). Article  ADS  MathSciNet  Google Scholar  * Bhaseen,

M. J., Mayoh, J., Simons, B. D. & Keeling, J. Dynamics of nonequilibrium Dicke models. _Phys. Rev. A_ 85, 013817 (2012). Article  ADS  Google Scholar  * See Supplemental Material. *

Keeling, J., Bhaseen, M. J. & Simons, B. D. Collective Dynamics of Bose-Einstein Condensates in Optical Cavities. _Phys. Rev. Lett._ 105, 043001 (2010). Article  ADS  Google Scholar  *

Kirton, P. & Keeling, J. Superradiant and lasing states in driven-dissipative Dicke models. _N. J. Phys._ 20, 015009 (2018). Article  MathSciNet  Google Scholar  * Gutiérrez-Jáuregui, R.

& Carmichael, H. J. Dissipative quantum phase transitions of light in a generalized Jaynes-Cummings-Rabi model. _Phys. Rev. A_ 98, 023804 (2018). Article  ADS  Google Scholar  *

Shchadilova, Y., Roses, M. M., Dalla Torre, E. G., Lukin, M. D. & Demler, E. Fermionic formalism for driven-dissipative multilevel systems. _Phys. Rev. A_ 101, 013817 (2020). Article 

ADS  MathSciNet  Google Scholar  * Stitely, K. C., Giraldo, A., Krauskopf, B. & Parkins, S. Lasing and counter-lasing phase transitions in a cavity-QED system. _Phys. Rev. Res._ 4,

023101 (2022). Article  Google Scholar  * Buča, B. & Prosen, T. A note on symmetry reductions of the Lindblad equation: transport in constrained open spin chains. _N. J. Phys._ 14,

073007 (2012). Article  MathSciNet  Google Scholar  * Albert, V. V. & Jiang, L. Symmetries and conserved quantities in Lindblad master equations. _Phys. Rev. A_ 89, 022118 (2014).

Article  ADS  Google Scholar  * Strogatz, S. _Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry and Engineering, Studies in nonlinearity_. (Westview, Cambridge,

MA, 2000). Google Scholar  * Keeling, J., Bhaseen, M. & Simons, B. Fermionic Superradiance in a Transversely Pumped Optical Cavity. _Phys. Rev. Lett._ 112, 143002 (2014). Article  ADS 

Google Scholar  * Soriente, M., Donner, T., Chitra, R. & Zilberberg, O. Dissipation-Induced Anomalous Multicritical Phenomena. _Phys. Rev. Lett._ 120, 183603 (2018). Article  ADS  Google

Scholar  * Meiser, D., Ye, J., Carlson, D. R. & Holland, M. J. Prospects for a millihertz-linewidth laser. _Phys. Rev. Lett._ 102, 163601 (2009). Article  ADS  Google Scholar  * Scully,

M. O. & Zubairy, M. S. _Quantum optics_. (Cambridge university press, Cambridge, 1997). Book  Google Scholar  * Soh, D. B. S., Rogers, C., Gray, D. J., Chatterjee, E. & Mabuchi, H.

Optical nonlinearities of excitons in monolayer MoS2. _Phys. Rev. B_ 97, 165111 (2018). Article  ADS  Google Scholar  * Keeling, J., Marchetti, F. M., Szymańska, M. H. & Littlewood, P.

B. Collective coherence in planar semiconductor microcavities. _Semicond. Sci. Technol._ 22, R1 (2007). Article  Google Scholar  * Kroeze, R. M., Marsh, B. P., Lin, K.-Y., Keeling, J. &

Lev, B. L. High Cooperativity Using a Confocal-Cavity-QED Microscope. _PRX Quantum_ 4, 020326 (2023b). Article  ADS  Google Scholar  * Arnardottir, K. B., Moilanen, A. J., Strashko, A.,

Törmä, P. & Keeling, J. Multimode organic polariton lasing. _Phys. Rev. Lett._ 125, 233603 (2020). Article  ADS  Google Scholar  * Levenberg, K. A method for the solution of certain

non-linear problems in least squares. _Quart. Appl. Math._ 2, 164 (1944). Article  MathSciNet  Google Scholar  * Marquardt, D. W. An Algorithm for Least-Squares Estimation of Nonlinear

Parameters. _J. Soc. Ind. Appl. Math._ 11, 431 (1963). Article  MathSciNet  Google Scholar  * Virtanen, P. et al. SciPy 1.0: fundamental algorithms for scientific computing in Python. _Nat.

Methods_ 17, 261 (2020). Article  Google Scholar  * Moré, J. J., B. S., Garbow and K. E., Hillstrom, User guide for MINPACK-1, Tech. Rep. https://cds.cern.ch/record/126569 (Argonne Nat.

Lab., Argonne, IL, 1980). * Glendinning, P., Stability, Instability and Chaos: An Introduction to the Theory of Nonlinear Differential Equations, 1st ed.

https://doi.org/10.1017/CBO9780511626296 (Cambridge University Press, 1994). * Johansson, J., Nation, P. & Nori, F. QuTiP 2: A Python framework for the dynamics of open quantum systems.

_Comput. Phys. Commun._ 184, 1234 (2013). Article  ADS  Google Scholar  Download references ACKNOWLEDGEMENTS We acknowledge helpful discussions with T. Heinz, A. J. Daley, H. S. Hiller, D.

Lao, R. M. Kroeze, B. P. Marsh, and H. S. Hunt. J.K. and B.L.L. acknowledge funding from the Gordon and Betty Moore Foundation (grant number GBMF10693). Large-scale simulations were

performed on the Sherlock cluster, provided by Stanford University and the Stanford Research Computing Center. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Physics, Stanford

University, Stanford, CA, 94305, USA Alexander N. Bourzutschky & Benjamin L. Lev * E. L. Ginzton Laboratory, Stanford University, Stanford, CA, 94305, USA Alexander N. Bourzutschky &

 Benjamin L. Lev * Department of Applied Physics, Stanford University, Stanford, CA, 94305, USA Benjamin L. Lev * SUPA, School of Physics and Astronomy, University of St. Andrews, St.

Andrews, KY16 9SS, United Kingdom Jonathan Keeling Authors * Alexander N. Bourzutschky View author publications You can also search for this author inPubMed Google Scholar * Benjamin L. Lev

View author publications You can also search for this author inPubMed Google Scholar * Jonathan Keeling View author publications You can also search for this author inPubMed Google Scholar

CONTRIBUTIONS B.L.L. and J.K. designed the research. A.N.B. performed the computations with input from J.K. All authors contributed to writing the manuscript. CORRESPONDING AUTHOR

Correspondence to Jonathan Keeling. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains

neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTAL INFORMATION RIGHTS AND PERMISSIONS OPEN ACCESS This

article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as

you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party

material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s

Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.

To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Bourzutschky, A.N., Lev, B.L. & Keeling,

J. Raman-phonon-polariton condensation in a transversely pumped cavity. _npj Quantum Mater._ 9, 81 (2024). https://doi.org/10.1038/s41535-024-00693-9 Download citation * Received: 12 May

2024 * Accepted: 28 September 2024 * Published: 17 October 2024 * DOI: https://doi.org/10.1038/s41535-024-00693-9 SHARE THIS ARTICLE Anyone you share the following link with will be able to

read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing

initiative