Implementation of quantum imaginary-time evolution method on nisq devices by introducing nonlocal approximation

ABSTRACT The imaginary-time evolution method is a well-known approach used for obtaining the ground state in quantum many-body problems on a classical computer. A recently proposed quantum

imaginary-time evolution method (QITE) faces problems of deep circuit depth and difficulty in the implementation on noisy intermediate-scale quantum (NISQ) devices. In this study, a nonlocal

approximation is developed to tackle this difficulty. We found that by removing the locality condition or local approximation (LA), which was imposed when the imaginary-time evolution

operator is converted to a unitary operator, the quantum circuit depth is significantly reduced. We propose two-step approximation methods based on a nonlocality condition: extended LA (eLA)

and nonlocal approximation (NLA). To confirm the validity of eLA and NLA, we apply them to the max-cut problem of an unweighted 3-regular graph and a weighted fully connected graph; we

comparatively evaluate the performances of LA, eLA, and NLA. The eLA and NLA methods require far fewer circuit depths than LA to maintain the same level of computational accuracy. Further,

we developed a “compression” method of the quantum circuit for the imaginary-time steps to further reduce the circuit depth in the QITE method. The eLA, NLA, and compression methods

introduced in this study allow us to reduce the circuit depth and the accumulation of error caused by the gate operation significantly and pave the way for implementing the QITE method on

NISQ devices. SIMILAR CONTENT BEING VIEWED BY OTHERS THE EFFECT OF CLASSICAL OPTIMIZERS AND ANSATZ DEPTH ON QAOA PERFORMANCE IN NOISY DEVICES Article Open access 11 July 2024 QUANTUM

COMPUTING QUANTUM MONTE CARLO WITH HYBRID TENSOR NETWORK FOR ELECTRONIC STRUCTURE CALCULATIONS Article Open access 06 June 2024 NON-MARKOVIAN COST FUNCTION FOR QUANTUM ERROR MITIGATION WITH

DIRAC GAMMA MATRICES REPRESENTATION Article Open access 16 November 2023 INTRODUCTION Quantum computers, initially proposed by Feynmann1, were reported by Benioff2, Deutsch3,4, Grover5, and

Shor6 to have great potential that could overwhelmingly surpass that of classical computers. Furthermore, Google experimentally demonstrated quantum supremacy, which is the refutation of the

extended Church–Turing thesis, proving the feasibility of quantum computers and raising the expectation for solving practical problems that a classical computer cannot address7. Quantum

computers can efficiently solve problems in the BQP (bounded-error quantum polynomial) complexity class8 and verify an answer to a problem in the QMA (quantum Merlin–Arthur) complexity

class9. One of the actively researched problems for quantum computers is combinatorial optimization, which is an NP-hard problem10. Combinatorial optimization problems are closely related to

our daily lives, and they include the traveling salesman problem11, scheduling problem12, and SAT (satisfiability problem) solver13. Although combinatorial optimization problems are

NP-hard, some quantum algorithms were shown to be superior to the classical ones. Grover’s algorithm is already known to improve the computational cost with quadratic speedup when compared

with classical computers14,15. It has been reported that quantum annealing is faster than simulated annealing in several cases16,17,18,19,20. Recently, quantum approximate optimization

algorithm (QAOA) has been researched owing to its superiority over classical algorithms, which was demonstrated at the time of its proposal21. However, with the development of classical

algorithms22, the quantum advantage of QAOA is now an open question. Under these circumstances, it is challenging for researchers all over the world to employ existing or near-future quantum

computers to achieve tasks that are very difficult or impossible using classical computers. Currently available quantum computers are noisy intermediate-scale quantum (NISQ) devices23.

Further, conventional quantum algorithms, such as Grover’s algorithm, require many gate operations and they cannot be implemented on NISQ devices with no error correction due to short

coherence time. Recently, classical-quantum hybrid algorithms called variational quantum eigensolver (VQE)24,25, and QAOA21,26,27,28,29,30 have been proposed for NISQ devices. In these

methods, ansatz states with parameters are implemented on quantum circuits, and the parameters included in the ansatz states are optimized on a classical computer. While VQE and QAOA can be

realized with a limited number of quantum operations and have good noise tolerance, it is difficult to determine the ansatz states properly and converge high-dimensional parameters31. For

quantum many-body problems, an imaginary-time evolution method is a known computational method to identify the ground state. The imaginary-time evolution method selectively extracts the

ground-state component by performing time evolution in the direction of imaginary time. Various combinatorial optimization problems are converted to a Hamiltonian format, and their

corresponding Hamiltonian is derived32. Thus, it is possible to solve the combinatorial optimization problem using the imaginary-time evolution method. The implementation of the

imaginary-time evolution method on a quantum computer involves a critical problem in that the imaginary-time evolution operator is a nonunitary operator, and therefore, it cannot implement

the imaginary-time evolution method on a quantum computer in its current state. To overcome this challenge, two quantum imaginary-time evolution (QITE) methods—one that assumes an ansatz

state and another that does not—were proposed in previous studies33,34. The method that assumes the ansatz state traces the imaginary-time evolution of the parameters contained in the ansatz

state33,35,36. The other method introduces a unitary operation to reproduce the state on which the imaginary-time evolution operator has acted accurately without assuming an ansatz

state34,37,38. We focus on the QITE method without the ansatz assumption and apply it to the optimization problems. The QITE method requires defining a domain size, which determines the

accuracy of reproducing the imaginary-time evolution operator. The quantum circuit of an imaginary-time step scales exponentially with respect to this domain size. Besides, as an additional

quantum circuit is added at each imaginary-time step, the quantum circuit becomes deeper in proportion to the lapse of imaginary time34. These two features make it difficult to implement the

QITE method on NISQ devices. Therefore, we propose two approximations and one computational technique to overcome this difficulty. We succeeded in significantly reducing the quantum circuit

depth of the QITE method, and we applied the developed algorithms to the max-cut problem, which is an NP-hard problem. For the max-cut problem, we chose an unweighted 3-regular graph and a

weighted fully connected graph. The latter is a problem known as the classification problem in the context of unsupervised machine learning39,40. RESULTS UNITARIZATION OF IMAGINARY-TIME

EVOLUTION OPERATORS Consider a scenario wherein a Hamiltonian \(\hat{H}\) is given for the optimization problem considered in this study. The Hamiltonian \(\hat{H}\) is expressed as the

summation of some partial Hamiltonians \(\hat{h}[m]\) as \(\hat{H}=\mathop{\sum }\nolimits_{m = 1}^{{N}_{{\rm{ham}}}}\hat{h}[m]\), where _N_ham is the number of the partial Hamiltonians. The

max-cut problem, which is a computational target of this work, is represented by the Hamiltonian in the form of Ising spins and can be mapped to the Pauli-operator representation for qubits

in a straightforward manner. In the case of the Hamiltonian of quantum chemistry, each partial Hamiltonian can be mapped to the Pauli-operator representation on qubits via the Bravyi–Kitaev

representation41 or Jordan–Wigner representation42. For a given Hamiltonian, the ground state is obtained by using the imaginary-time evolution method. We apply the imaginary-time evolution

operator defined by \({{\rm{e}}}^{-\tau \hat{H}}\), where _τ_ is the imaginary time to reach the initial (_τ_ = 0) state of the system, \(\left|{{\Psi }}(\tau =0)\right\rangle\); and

\({{\rm{e}}}^{-\tau \hat{H}}\left|{{\Psi }}(\tau =0)\right\rangle\). The imaginary-time evolution operator is decomposed by a first-order Suzuki–Trotter decomposition into ones with a small

imaginary-time step Δ_τ_ (_τ_ ≡ Δ_τ_ × _N_step) of the individual partial Hamiltonians \(\hat{h}[m]\). $${{\rm{e}}}^{-\tau \hat{H}}=\mathop{\prod

}\limits_{n=1}^{{N}_{{\rm{step}}}}\mathop{\prod }\limits_{m=1}^{{N}_{{\rm{ham}}}}{{\rm{e}}}^{-{{\Delta }}\tau \hat{h}[m]}+{\mathcal{O}}({{\Delta }}{\tau }^{2})\ \ .$$ (1) Because the

operators of the imaginary-time evolution are nonunitary, they cannot be directly implemented as a gate operation on a quantum computer. In the QITE method, the unitary operator

\({e}^{-i{{\Delta }}\tau {\hat{A}}_{n}[m]}\) is defined such that it reproduces the state \({{\rm{e}}}^{-{{\Delta }}\tau \hat{H}}\left|{{{\Psi }}}_{n}\right\rangle\) for a given state

\(\left|{{{\Psi }}}_{n}\right\rangle \equiv \left|{{\Psi }}(\tau =n{{\Delta }}\tau )\right\rangle\). We determine the Hermitian operator \({\hat{A}}_{n}[m]\) that minimizes the following

residual norm. $${\left|\left|\frac{{{\rm{e}}}^{-{{\Delta }}\tau \hat{h}[m]}\left|{{{\Psi }}}_{n}\right\rangle }{\sqrt{\left\langle {{{\Psi }}}_{n}\right|{{\rm{e}}}^{-2{{\Delta }}\tau

\hat{h}[m]}\left|{{{\Psi }}}_{n}\right\rangle }}-{{\rm{e}}}^{-i{{\Delta }}\tau {\hat{A}}_{n}[m]}\left|{{{\Psi }}}_{n}\right\rangle \right|\right|}^{2}\ \ .$$ (2) NONLOCAL CONDITION FOR

IMAGINARY-TIME EVOLUTION OPERATORS We express the Hermitian operator \({\hat{A}}_{n}[m]\) as a linear combination of the _D_th order tensor products of Pauli operators

\(\{{\hat{I}}_{l},{\hat{\sigma }}_{X,l},{\hat{\sigma }}_{Y,l},{\hat{\sigma }}_{Z,l}\}\) acting on the _l_th qubit as $${\hat{A}}_{n}[m]={\mathop{\sum}\limits_{{l}_{k+1},\cdots ,{l}_{D}\in

{{\mathbb{L}}}_{m}}}^{\prime}\mathop{\sum}\limits_{{i}_{1}\cdots {i}_{D}}{a}_{{i}_{1}\cdots {i}_{D},{l}_{1}\cdots {l}_{D}}^{(n)}[m]{\hat{\sigma }}_{{i}_{1},{l}_{1}(m)}\otimes \cdots \otimes

{\hat{\sigma }}_{{i}_{D},{l}_{D}},$$ (3) where the prime on the first summation symbol indicates removing the double counting of the repeated tensors. We defined \({{\mathbb{L}}}_{m}\) as

the set of \({N}_{{{\mathbb{L}}}_{m}}\) qubits, each of which is directly connected with those acted on by the partial Hamiltonian \(\hat{h}[m]\); however, \({{\mathbb{L}}}_{m}\) does not

contain the qubits acted on by \(\hat{h}[m]\) [see Fig. 1a]. The parameter _D_, which is called the domain size, satisfies \(k\,\leqq \,D\,\leqq \,k+{N}_{{{\mathbb{L}}}_{m}}\), where we

assumed the partial Hamiltonian \(\hat{h}[m]\) to be written by a tensor product of the _k_th order. {_l_1(_m_),⋯,_l__k_(_m_)} is the set of qubits contained in the partial Hamiltonian

\(\hat{h}[m]\). The summation in Eq. (3) is taken over all combinations of _D_ − _k_ qubits, {_l__k_ + 1(_m_),⋯, _l__D_(_m_)}, and chosen from \({{\mathbb{L}}}_{m}\). _D_ is an input

parameter that represents the level of approximation; a larger _D_ indicates that the imaginary-time evolution operator is expressed using higher-order tensor products and the residual norm

in Eq. (2) shows a smaller value, which leads to a better approximation. Note that for _D_ = _N_bit, with _N_bit being the number of qubits, the residual norm in Eq. (2) vanishes when

minimized, yielding the exact imaginary-time evolution operator. In this context, the parameter _D_ represents a truncation level. We consider a scenario where the domain size _D_

incorporates all elements in \({{\mathbb{L}}}_{m}\), namely \(D=k+{N}_{{{\mathbb{L}}}_{m}}\), and then Eq. (3) reproduces the operator _A__n_[_m_] introduced in reference34. This implies

that Eq. (3) is a natural extension of the approximation introduced in reference34. We call the method for determining the operator _A__n_[_m_] defined in reference34 local approximation

(LA) for comparison with later approximation. Then, we refer to the method defined in Eq. (3) as extended local-approximation (eLA). The following notation is used to indicate the domain

size _D_: e.g., LA with _D_ = 6 is denoted by LA-D6. Note that, for LA, it is a well-defined approximation only when the domain size \(D=k+{N}_{{{\mathbb{L}}}_{m}}\), and the value of _D_

that can be taken is limited by the Hamiltonian. With an ill-defined domain size _D_ in LA, we found that the calculation accuracy decreased, which is called “Inexact QITE" in

reference34. Note that eLA can remove such constraints on the Hamiltonian and flexibly determine the parameter _D_ by considering the linear combination for qubits. This flexibility is

obvious in the max-cut problem of the fully connected graph. Solving the minimization problem in Eq. (2) to determine the coefficients \({a}_{\{i,l\}}^{(n)}[m]\) results in the linear

equation _S_(_n_)_a_(_n_)[_m_] = _b_(_n_)[_m_], which can be solved using a classical computer. Here, \({S}_{\{i,{l}_{i}\}\{j,{l}_{j}\}}^{(n)}=\left\langle {{{\Psi }}}_{n}\right|{\hat{\sigma

}}_{\{i,{l}_{i}\}}^{\dagger }{\hat{\sigma }}_{\{j,{l}_{j}\}}\left|{{{\Psi }}}_{n}\right\rangle\) and \({b}_{\{i,{l}_{i}\}}^{(n)}[m]=\left\langle {{{\Psi }}}_{n}\right|{\hat{\sigma

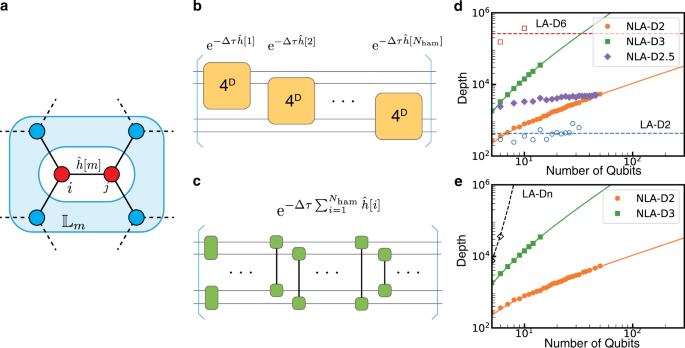
}}_{\{i,{l}_{i}\}}^{\dagger }\hat{h}[m]\left|{{{\Psi }}}_{n}\right\rangle\). Figure 1b shows a schematic of the quantum circuit representing one imaginary-time step of LA. In LA, the

operator of the imaginary-time evolution is approximated by the tensor products of Pauli operators up to the _D_th order; therefore, 4_D_ gate operations are required for each partial

Hamiltonian. The total number of gate operations for one step of the imaginary-time evolution is _N_ham4_D_. Table 1 summarizes the size of the linear equation of the LA per step of the

imaginary-time evolution and the number of gate operations per qubit, where _N_bit is the total number of qubits. Furthermore, this study proposes another approximation method for

\({\hat{A}}_{n}\) in the following form: $${\hat{A}}_{n}={\mathop{\sum}\limits_{{l}_{1},\cdots {l}_{D}}}^{\prime}\mathop{\sum}\limits_{{i}_{1},\cdots {i}_{D}}{a}_{{i}_{1}\cdots

{i}_{D},{l}_{1}\cdots {l}_{D}}^{(n)}{\hat{\sigma }}_{{i}_{1},{l}_{1}}\otimes \cdots \otimes {\hat{\sigma }}_{{i}_{D},{l}_{D}}.$$ (4) The difference from Eq. (3) is that we remove the

restriction on the set {_l_1(_m_),⋯ _l__k_(_m_)} and extend the summation over qubits to incorporate all possible combinations of _D_ qubits {_l_1(_m_),⋯ _l__D_(_m_)}. We call this an NLA.

As per this definition, we expand the Hermitian operator, \({\hat{A}}_{n}\), using tensor products of Pauli operators over all qubit combinations. Moreover, in LA and eLA, the tensor product

space describing \({\hat{A}}_{n}[m]\) is different depending on _m_, which is the partial Hamiltonian. The NLA has a notable feature in that the tensor product space that describes

\(\hat{A}[m]\) is the same for all _m_. Table 1 lists the size of the linear equations of the NLA per step of the imaginary-time evolution and the number of gate operations per qubit, where

the NLA requires only 4_D_ unitary operators in \({}_{{N}_{{\rm{bit}}}}{C}_{D}\) combinations for the quantum circuit in the first step of the imaginary-time evolution. Figure 1c shows the

schematic of the quantum circuit of the NLA for one step of the imaginary-time evolution (for _D_ = 2). REDUCTION EFFECT OF CIRCUIT DEPTH To clarify the accuracy and effectiveness of NLA, we

applied it to the max-cut problem, which is an NP-hard problem. The Hamiltonian of the max-cut problem in qubit representation is given in the following form containing second-order tensor

products32. $$\hat{H}=-\mathop{\sum}\limits_{(i,j)\in E}{d}_{i,j}\frac{1-{\hat{\sigma }}_{Z,i}{\hat{\sigma }}_{Z,j}}{2}$$ (5) As for the max-cut problem, we considered typical graphs such as

3-regular and fully connected graphs. The 3-regular graphs have three connected edges at every vertex, where _E_ is the set of edges contained in the graph and _d__i_,_j_ is the weight of

the edges connecting the _i_th and _j_th vertices. The circuit depths, when LA and NLA are applied to the max-cut problem, are shown in Fig. 1d for the 3-regular graph and Fig. 1e for the

fully connected graph because different graphs of the max-cut problem change the number of the partial Hamiltonian _N_ham; the necessary circuit depths for each approximation change

correspondingly. In Fig. 1d, e, the circuit depth calculated using Qiskit43 is plotted with points, and the plotted points are extrapolated. In the case of _k_-regular graphs, the number of

the partial Hamiltonians is given by _N_ham = _k__N_bit/2. It increases linearly with the number of vertices _N_bit so that the number of gate operations per qubit does not depend on the

number of qubits, as listed in Table 1. Thus, we extrapolated using \(y={\rm{const.}}\). In NLA, regardless of the structure of the Hamiltonian, the number of gate operations per qubit is

scaled by \({\mathcal{O}}({{N}_{{\rm{bit}}}}^{D-1})\) with respect to the number of qubits _N_bit because all combinations of \({}_{{N}_{{\rm{bit}}}}{C}_{D}\) are taken for gate operations

including the _D_th order tensor product. In Fig. 1d, the circuit depth of the NLA is extrapolated by the function fitted by _f_(_x_) = _x__D_ − 1. Note that in LA, _D_ = 3, 4, and 5 are not

well-defined in the 3-regular graph. Thus, _D_ = 6 is required, and 46 = 4096 gate operations are necessary for the imaginary-time evolution of one partial Hamiltonian, which leads to a

deeper circuit depth and difficulty in implementation on NISQ devices. In addition, the circuit depth required for LA-D6, compared to NLA-D2, NLA-D3, etc., is considerably higher in the

region with a small number of qubits. The circuit depth of the NLA becomes deeper than that of LA in the region where the number of qubits increases. In Fig. 1e, LA-D2 and eLA-D3 are not

shown for the fully connected graph (\({N}_{{\rm{ham}}}{ = }_{{N}_{{\rm{bit}}}}{C}_{2}\)) because the circuit depth of LA-D2 is equal to that of the NLA-D2, and that of eLA-D3 is equal to

that of NLA-D3. In addition, because the domain size has to be _D_ = _N_bit in LA, which is the exact imaginary-time evolution in a fully connected graph, and the circuit depth increases

exponentially with respect to the number of qubits. In NLA, it can be scaled down to the linear or quadratic function with respect to the number of qubits. This result indicates that the NLA

and eLA are efficient in reducing the circuit depth, especially when the number of partial Hamiltonians increases; further, these algorithms are effective for NISQ devices. CALCULATION

ACCURACY Simulations were performed after modifying the code provided in reference34. As an initial state, we adopted a state in which all states were superimposed with equal a priori

weights. We adopt a figure of merit to discuss the accuracy of the QITE method. $$r={{\rm{lim}}}_{\tau \to \infty }\frac{\left\langle {{\Psi }}(\tau )\right|\hat{H}\left|{{\Psi }}(\tau

)\right\rangle }{{E}_{{\rm{GS}}}}.$$ (6) The first target of the max-cut problem is an unweighted 3-regular graph with ten vertices, where _E_GS is the energy of the ground state, and it is

obtained from the exact diagonalization. The energy of the ground state is _E_GS = −12. It is known that designing a classical algorithm that achieves _r_ > 331/332 for an unweighted

3-regular graph is an NP-hard problem44. Further, the approximation accuracy of the current classical algorithm is _r_ ≈ 0.932645. Figure 2a shows the imaginary-time dependence of the

energy. The imaginary-time step was set to Δ_τ_ = 0.01. In LA-D2, as the imaginary-time _τ_ increased, the energy decreased exponentially in the beginning and converged to around −9, which

is higher than the exact solution by about 3. Another important point is that the energy does not monotonically decreases along the imaginary-time evolution. This behavior indicates that the

conversion of the operator of the imaginary-time evolution to the unitary operators is less accurate in expanding it in the space of LA-D2. Furthermore, the LA-D6 calculation result shows

_E_ = −11.99, which is the energy almost equal to the exact solution. We found that an approximation accuracy in the eLA-D3 is _E_ = − 11.17 (_r_ = 0.93) (the lowest value is _E_ = −11.33

(_r_ = 0.94)); in NLA-D2, _E_ = −11.42 (_r_ = 0.95); and in NLA-D3, _E_ = −12.00 (_r_ = 1.00). We found that eLA-D3 had an approximation accuracy similar to that of the classical algorithm,

and NLA-D2 had already exceeded the approximation accuracy of the classical algorithm. NLA-D3 shows better accuracy than NLA-D2 and can reach a nearly exact solution. Note that eLA and NLA

monotonically decrease the energy along the imaginary-time evolution with sufficiently good accuracy compared to LA-D2. This behavior was confirmed not only for NLA-D2 but also for NLA-D3

and others. As can be seen from Fig. 1d, in LA-D6, the circuit depth of one imaginary-time step is 369757, while the circuit depth in the NLA-D2 is 789. This implies the circuit depth of NLA

can be significantly shallower than that of LA. While NLA-D3 has extremely high accuracy, its circuit depth increases with a quadratic function with respect to the number of qubits. Then,

we developed NLA-D2.5 to keep the scaling of the circuit depth as linear as NLA-D2 while maintaining the accuracy of NLA-D3, which is an approximation to expand the space of

\({\hat{A}}_{n}\) to the space involving the second-order tensor products incorporated by NLA-D2 and the third-order tensor products by eLA-D3. Thus, by incorporating some portions of bases

of eLA-D3 into those of NLA-D2, computational scaling can be made linear with respect to the number of qubits, which makes it applicable even in regions with a large number of qubits. Figure

1d shows that the circuit depth is almost the same as that of NLA-D2 for 50 qubits or more, which means that the circuit depth can be significantly reduced compared to that of NLA-D3. In

addition, the calculation result of NLA-D2.5 is _E_ = −11.95 and _r_ = 0.99, which gives a good approximation accuracy with a small circuit depth. Here, for further consideration, we

decomposed the state \(\left|{{\Psi }}(\tau )\right\rangle ={{\rm{e}}}^{-\tau \hat{H}}\left|{{\Psi }}(\tau =0)\right\rangle\) into the eigenstate components of the Hamiltonian, and the

calculated _n_(_E_) ≡ ∑_i_∣〈_i_∣Ψ(_τ_)〉∣2_δ_(_E_ − _E__i_) as a function of energy _E_ at each imaginary-time step _τ_ is plotted in Fig. 2b where \(\left|i\right\rangle\) is the eigenstate

of \(\hat{H}\) and _E__i_ is the eigen energy of \(\left|i\right\rangle\). Here, we note that the ground state of the eigenstate component _n_(_E_GS) is equal to the so-called fidelity

defined as _F_ = ∣〈Ψ(_τ_)∣ΨGS〉∣2. The ground state can be observed with probabilities of _n_(_E_GS) = 0.60 for eLA-D3 (at maximum, _n_(_E_GS, _τ_ = 2.87) = 0.65), _n_(_E_GS) = 0.69 for

NLA-D2, _n_(_E_GS) = 0.97 for NLA-D2.5, and _n_(_E_GS) = 1.00 for NLA-D3. The imaginary-time dependence of the probability of the first excited state is also plotted. For the first excited

state, it is observed that the probability is amplified up to _τ_ = 1, and it starts to decrease, which increases the ground-state probability. Next, we deal with another computational model

called a weighted fully connected graph (classification problem). The coupling constants _d__i_,_j_ were given by random numbers. The ground-state energy is _E_GS = −57.993. In addition,

the imaginary-time step is set to Δ_τ_ = 0.01. In the classification problem, as shown in Fig. 2e, each graph vertex is colored red or blue. In LA-D2, as in the 3-regular graph, we observed

that the energy does not necessarily decrease monotonically. The energy of eLA-D3 is lower than that of NLA-D2; _E_ = −57.504 (_r_ = 0.99) for eLA-D3, _E_ = −57.026 (_r_ = 0.98) for NLA-D2,

and _E_ = −57.985 (_r_ = 0.99) for NLA-D3 (Fig. 2c). From the viewpoint of the component analyses of the states, the ground state and the first excited state are pseudo-degenerate (Fig. 2e),

and therefore, the probability of the first excited state remains at the same level as the ground state even around _τ_ = 2 when the energy converges sufficiently (Fig. 2d). In NLA, the

first excited state gradually decays along with the imaginary-time evolution; however, a sufficiently long imaginary-time evolution is necessary. In particular, NLA-D2 behaves similarly to

NLA-D3, and NLA-D2 is sufficiently accurate to obtain the ground state in actual applications. We now consider why the accuracy of eLA and NLA is better than that of LA with a relatively

small domain size _D_. From the actual application results of eLA-D3, we found that the \({b}_{\{i,{l}_{i}\}}^{(n)}[m]=\left\langle {{{\Psi }}}_{n}\right|{\hat{\sigma

}}_{\{i,{l}_{i}\}}^{\dagger }\hat{h}[m]\left|{{{\Psi }}}_{n}\right\rangle \approx 0\) when the Pauli operator \({\hat{\sigma }}_{\{i,{l}_{i}\}}^{\dagger }\) and \(\hat{h}[m]\) do not

intersect each other. With a rough approximation for such cases, \({b}_{\{i,{l}_{i}\}}^{(n)}[m]=\left\langle {{{\Psi }}}_{n}\right|{\hat{\sigma }}_{\{i,{l}_{i}\}}^{\dagger

}\hat{h}[m]\left|{{{\Psi }}}_{n}\right\rangle =0\), a sparsity in the coefficients of _A__n_ can be deduced, which eLA highlight and leverage. This fact means that the terms that would

require a large domain size _D_ in LA can be efficiently captured with a smaller domain size D in eLA, leading to its high accuracy. Furthermore, by considering that the definition of NLA is

expanded from that of eLA, NLA can improve further the accuracy of eLA. COMPRESSION OF IMAGINARY-TIME STEPS The approximation accuracy of the NLA and its circuit depth have been discussed.

The “compression of imaginary-time steps” is introduced in this section for further reduction of the number of gate operations in NLA. Figure 3a shows a schematic of the compression

technique. When the imaginary-time step Δ_τ_ is sufficiently small, the time-evolution operators can be compressed into a single exponential form via the reverse Suzuki–Trotter decomposition

$$\mathop{\prod }\limits_{n=1}^{{N}_{{\rm{comp}}}}\exp (-i{{\Delta }}\tau \hat{{A}_{n}})=\exp (-i{{\Delta }}\tau \mathop{\sum

}\limits_{n=1}^{{N}_{{\rm{comp}}}}\hat{{A}_{n}})+{\mathcal{O}}({{\Delta }}{\tau }^{2}),$$ (7) where _N_comp is the number of compressed steps. It is necessary to choose an appropriate

_N_comp within the range that guarantees sufficient accuracy for the Suzuki–Trotter decomposition because its accuracy decreases if the _N_comp becomes large. To determine the specific

_N_comp in this work, we increased the _N_comp parameter by one at every time-evolution step until the total energy increases. In actual QITE calculations, _N_comp is not necessarily a

constant throughout the calculation. This method enables the reduction of quantum circuits to as small as 1/_N_comp. We discussed the error of the second order for Δ_τ_ in the compression

method in Supplementary Note 1. The graph used for the calculation is the same as that in Fig. 2a, b, which is a 3-regular graph with ten vertices. Figure 3 shows the results of the

compression technique for the QITE. In Fig. 3b, the time the compression ended is plotted as a blue circle. In the case of Fig. 3b, the quantum circuit depth is significantly reduced by the

compression technique to four compressed imaginary-time steps, and the energy at _τ_ = 10 is _E_ = −11.43 (_r_ = 0.95) without and _E_ = −11.59 (_r_ = 0.97) with the compression technique.

We found that sufficient accuracy was achieved regardless of the compression, which indicates that compression does not affect the results. It may be assumed that the compressed technique

has a lower energy than that of the uncompressed calculation; a detailed investigation revealed that this was attributed to the accidental acceleration of the convergence by compression.

Figure 3c plots the component analyses of the wavefunctions during the imaginary-time evolution with and without the compression method. Finally, the probability of obtaining a ground state

is \(n({E}_{\min })=0.76\) with and \(n({E}_{\min })=0.73\) without the compression technique. The “compression of imaginary-time steps” is effective in reducing the circuit depth, and

simultaneously, it reduces the noise associated with the gate operations. We discuss the results of the simulation with noise. The actual qubits are currently connected only with neighboring

sites; however, in this study, we simulated a fully connected model. For implementation on an actual quantum computer, in which only adjacent sites are connected, a SWAP gate can be used

with an overhead of \({\mathcal{O}}(\sqrt{{N}_{{\rm{bit}}}})\)46. For example, QAOA uses a SWAP network47,48 to implement a \({\mathcal{O}}({N}_{{\rm{bit}}})\) overhead49. We describe the

quantum circuit of NLA-D2 of the QITE method for an adjacent-coupling circuit using the SWAP network in Supplementary Note 2. Figure 3d shows the simulation results of the max-cut problem

for an unweighted graph with four vertices. The coefficients \({a}_{\{i,l\}}^{(n)}\) in Eq. (4) for the noisy calculation are the same as those for the non-noisy calculation. The noiseless

condition without compression results in _E_ = −3.94, which is close to the exact solution _E_ = −4.00 around _τ_ = 5. However, the circuit depth is 922 (Δ_τ_ = 0.5), and the simulation

result with noise is _E_ = −3.13, which is far from the exact solution. This gap was attributed to the accumulation of errors caused by an increase in circuit depth. The result with

compression is _E_ = −3.85 in the case without noise; however, the circuit depth is 163, and the effect of noise is expected to be less sensitive. In fact, the simulation result with noise

is _E_ = −3.63, which shows that the noise can be reduced with compression. Thus, it has been shown that the “compression” method of quantum circuits has the advantage of reducing the

accumulation of errors. DISCUSSION In this study, we proposed two-step approximation methods based on nonlocality: eLA and NLA. We applied them to the Max-cut problem of an unweighted

3-regular graph and a weighted fully connected graph, and comparatively validated the performances of LA, eLA, and NLA. We found that NLA requires significantly less circuit depth than LA

while maintaining the same level of computational accuracy. For example, when we request the classical approximation limit in the QITE calculations, the circuit depth required for a single

imaginary-time step can be significantly reduced from 369,757 for LA to 789 for NLA when applying it to a 3-regular graph, and from about 314,000 for LA to 789 for NLA when applying it to a

fully connected graph. Further, we developed a “compression” technique of the imaginary-time evolution steps to further reduce the circuit depth in the QITE method. With this compression

method, we succeeded in further reducing the circuit depth. We showed that the reduction in circuit depth using this compression method has a secondary effect of reducing the accumulation of

error caused by the gate operation. Thus, it is an effective method for realization on NISQ devices. The eLA, NLA, and compression methods introduced in this study enable us to

significantly reduce the circuit depth and the accumulation of error caused by the gate operation and have paved the way for the realization of the QITE method on NISQ devices. METHODS NOISY

SIMULATION OF QITE METHOD Our numerical simulations were performed after implementing the eLA, NLA, and compression method on the code provided in reference34. The simulation of the quantum

noise’s presence is performed with the implementation of the QITE method at the level of the NLA-D2 on the IBM Qiskit quantum simulator. Although almost all actual quantum devices’ qubit

connectivity is restricted, we simulated the QITE method based on the fully connected coupling. For implementation on a device connected only with neighboring qubits, we provide a circuit of

the QITE method using the SWAP network in Supplementary Note 2. The error model of the gate was constructed from the thermal relaxation time (_T_1, _T_2) = (100 μs, 80 μs), and the gate

time (_T__g_1, _T__g_2) = (0.02 ns, 0.1 ns). The noise simulation was performed by introducing the readout errors (_p_00, _p_01, _p_10, _p_11) = (0.995, 0.005, 0.02, 0.98). These parameters

were assumed to be close to the actual values of IBMQ50. NOTE ADDED TO PROOF During our review of this paper, we noticed an independent work-related “compression method” being done in

parallel51. DATA AVAILABILITY The datasets generated and/or analyzed during the current study are available from the corresponding author on reasonable request. CODE AVAILABILITY The code

depeloped for the current study is available from the corresponding author on reasonable request. REFERENCES * Feynman, R. P. Simulating physics with computers. _Int. J. Theor. Phys._ 21,

467–488 (1982). Article  MathSciNet  Google Scholar  * Benioff, P. The computer as a physical system: a microscopic quantum mechanical hamiltonian model of computers as represented by turing

machines. _J. Stat. Phys._ 22, 563–591 (1980). Article  ADS  MathSciNet  Google Scholar  * Deutsch, D. Quantum theory, the church–turing principle and the universal quantum computer. _Proc.

R. Soc. Lond. A Math. Phys. Sci._ 400, 97–117 (1985). ADS  MathSciNet  MATH  Google Scholar  * Deutsch, D. & Jozsa, R. Rapid solution of problems by quantum computation. _Proc. R. Soc.

Lond. Ser. A: Math. Phys. Sci._ 439, 553–558 (1992). Article  ADS  MathSciNet  Google Scholar  * Grover, L. K. A fast quantum mechanical algorithm for database search. In _Proc.

Twenty-eighth Annual ACM Symposium on Theory of Computing_, 212–219 (1996). * Shor, P. W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer.

_SIAM Rev._ 41, 303–332 (1999). Article  ADS  MathSciNet  Google Scholar  * Arute, F. et al. Quantum supremacy using a programmable superconducting processor. _Nature_ 574, 505–510 (2019).

Article  ADS  Google Scholar  * Bernstein, E. & Vazirani, U. Quantum complexity theory. _SIAM J. Comput._ 26, 1411–1473 (1997). Article  MathSciNet  Google Scholar  * Kitaev, A. Y.,

Shen, A., Vyalyi, M. N. & Vyalyi, M. N. _Classical and Quantum Computation_. 47 (American Mathematical Soc., 2002). * Hyafil, L. & Rivest, R. L. _Graph Partitioning and Constructing

Optimal Decision Trees are Polynomial Complete Problems_ (IRIA, Laboratoire de Recherche en Informatique et Automatique, 1973). * Lawler, E. L. _The Traveling Salesman Problem: A Guided Tour

of Combinatorial Optimization. Wiley-Interscience Series in Discrete Mathematics_ (John Wiley & Sons,1985). * Ho, N. B. & Tay, J. C. Genace: an efficient cultural algorithm for

solving the flexible job-shop problem. In _Proc. 2004 Congress on Evolutionary Computation (IEEE Cat. No. 04TH8753)_, Vol. 2, 1759–1766 (IEEE, 2004). * Karp, R. M. Reducibility among

combinatorial problems. In _Complexity of Computer Computations_, 85–103 (Springer, 1972). * Durr, C. & Hoyer, P. A quantum algorithm for finding the minimum. arXiv. quant-ph/9607014

(1996). * Baritompa, W. P., Bulger, D. W. & Wood, G. R. Grover’s quantum algorithm applied to global optimization. _SIAM J. Optim._ 15, 1170–1184 (2005). Article  MathSciNet  Google

Scholar  * Kadowaki, T. & Nishimori, H. Quantum annealing in the transverse ising model. _Phys. Rev. E_ 58, 5355 (1998). Article  ADS  Google Scholar  * Farhi, E. et al. A quantum

adiabatic evolution algorithm applied to random instances of an np-complete problem. _Science_ 292, 472–475 (2001). Article  ADS  MathSciNet  Google Scholar  * Johnson, M. W. et al. Quantum

annealing with manufactured spins. _Nature_ 473, 194–198 (2011). Article  ADS  Google Scholar  * Albash, T. & Lidar, D. A. Demonstration of a scaling advantage for a quantum annealer

over simulated annealing. _Phys. Rev. X_ 8, 031016 (2018). Google Scholar  * Susa, Y. et al. Quantum annealing of the p-spin model under inhomogeneous transverse field driving. _Phys. Rev.

A_ 98, 042326 (2018). Article  ADS  Google Scholar  * Farhi, E., Goldstone, J. & Gutmann, S. A quantum approximate optimization algorithm. arXiv. https://arxiv.org/abs/1411.4028 (2014).

* Barak, B. et al. Beating the random assignment on constraint satisfaction problems of bounded degree. arXiv. https://arxiv.org/abs/1505.03424 (2015). * Preskill, J. Quantum computing in

the nisq era and beyond. _Quantum_ 2, 79 (2018). Article  Google Scholar  * Peruzzo, A. et al. A variational eigenvalue solver on a photonic quantum processor. _Nat. Commun._ 5, 4213 (2014).

Article  ADS  Google Scholar  * McClean, J. R., Romero, J., Babbush, R. & Aspuru-Guzik, A. The theory of variational hybrid quantum-classical algorithms. _N. J. Phys._ 18, 023023

(2016). Article  Google Scholar  * Otterbach, J. et al. Unsupervised machine learning on a hybrid quantum computer. arXiv. https://arxiv.org/abs/1712.05771 (2017). * Moll, N. et al. Quantum

optimization using variational algorithms on near-term quantum devices. _Quantum Sci. Technol._ 3, 030503 (2018). Article  ADS  Google Scholar  * Wang, Z., Hadfield, S., Jiang, Z. &

Rieffel, E. G. Quantum approximate optimization algorithm for maxcut: a fermionic view. _Phys. Rev. A_ 97, 022304 (2018). Article  ADS  Google Scholar  * Hadfield, S. et al. From the quantum

approximate optimization algorithm to a quantum alternating operator ansatz. _Algorithms_ 12, 34 (2019). Article  MathSciNet  Google Scholar  * Guerreschi, G. G. & Matsuura, A. Y. Qaoa

for max-cut requires hundreds of qubits for quantum speed-up. _Sci. Rep._ 9, 6903 (2019). Article  ADS  Google Scholar  * McClean, J. R., Boixo, S., Smelyanskiy, V. N., Babbush, R. &

Neven, H. Barren plateaus in quantum neural network training landscapes. _Nat. Commun._ 9, 1–6 (2018). Article  ADS  Google Scholar  * Lucas, A. Ising formulations of many np problems.

arXiv. https://arxiv.org/abs/1302.5843 (2014). * McArdle, S. et al. Variational ansatz-based quantum simulation of imaginary time evolution. _npj Quantum Inf._ 5, 1–6 (2019). Article  Google

Scholar  * Motta, M. et al. Determining eigenstates and thermal states on a quantum computer using quantum imaginary time evolution. _Nat. Phys._ 16, 205–210 (2020). Article  Google Scholar

  * Stokes, J., Izaac, J., Killoran, N. & Carleo, G. Quantum natural gradient. arXiv. https://arxiv.org/abs/1909.02108 (2019). * David, W., Christian, G. & Michael, K. Avoiding local

minima in variational quantum eigensolvers with the natural gradient optimizert. arXiv. https://arxiv.org/abs/2004.14666 (2020). * Yeter-Aydeniz, K., Pooser, R. C. & Siopsis, G.

Practical quantum computation of chemical and nuclear energy levels using quantum imaginary time evolution and lanczos algorithms. arXiv. https://arxiv.org/abs/1912.06226 (2019). * Beach, M.

J., Melko, R. G., Grover, T. & Hsieh, T. H. Making trotters sprint: a variational imaginary time ansatz for quantum many-body systems. _Phys. Rev. B_ 100, 094434 (2019). Article  ADS 

Google Scholar  * Jain, A. K., Murty, M. N. & Flynn, P. J. Data clustering: a review. _ACM Comput. Surv. (CSUR)_ 31, 264–323 (1999). Article  Google Scholar  * Jain, A. K. & Dubes,

R. C. _Algorithms for Clustering Data_ (Prentice-Hall, Inc., 1988). * Bravyi, S. B. & Kitaev, A. Y. Fermionic quantum computation. _Ann. Phys._ 298, 210–226 (2002). Article  ADS 

MathSciNet  Google Scholar  * Jordan, P. & Wigner, E. P. Über das paulische Äquivalenzverbot. _Eur. Phys. J._ 47, 631–651 (1928). ADS  MATH  Google Scholar  * Aleksandrowicz, G. et al.

Qiskit: an open-source framework for quantum computing. Accessed 16 Mar 2019. * Berman, P. & Karpinski, M. On some tighter inapproximability results (extended abstract). In _Proc. 26th

International Colloquium on Automata, Languages and Programming_, 200–209 (1999). * Goemans, M. X. & Williamson, D. P. Improved approximation algorithms for maximum cut and

satisfiability problems using semidefinite programming. _J. ACM_ 42, 1115–1145 (1995). Article  MathSciNet  Google Scholar  * Cheung, D., Maslov, D. & Severini, S. Translation techniques

between quantum circuit architectures. In _Proc.Workshop on Quantum Information Processing_ (2007). * Kivlichan, I. D. et al. Quantum simulation of electronic structure with linear depth

and connectivity. _Phys. Rev. Lett._ 120, 110501 (2018). Article  ADS  MathSciNet  Google Scholar  * Babbush, R. et al. Low-depth quantum simulation of materials. _Phys. Rev. X_ 8, 011044

(2018). Google Scholar  * Crooks, G. E. Performance of the quantum approximate optimization algorithm on the maximum cut problem. arXiv. https://arxiv.org/abs/1811.08419 (2018). * IBM

Quantum Experience Web Site. https://quantum-computing.ibm.com/. * Gomes, N. et al. Efficient step-merged quantum imaginary time evolution algorithm for quantum chemistry. _J. Chem. Theory

Comput._ 16, 6256–6266 (2020). Article  Google Scholar  Download references ACKNOWLEDGEMENTS This research was supported by MEXT as an Exploratory Challenge on Post-K computer (Frontiers of

Basic Science: Challenging the Limits) and by Grants-in-Aid for Scientific Research (A) (Grant Number 18H03770) from JSPS (Japan Society for the Promotion of Science). AUTHOR INFORMATION

AUTHORS AND AFFILIATIONS * Laboratory for Materials and Structures, Institute of Innovative Research, Tokyo Institute of Technology, Tokyo, Japan Hirofumi Nishi, Taichi Kosugi & 

Yu-ichiro Matsushita * Quemix Inc., Tokyo, Japan Hirofumi Nishi, Taichi Kosugi & Yu-ichiro Matsushita Authors * Hirofumi Nishi View author publications You can also search for this

author inPubMed Google Scholar * Taichi Kosugi View author publications You can also search for this author inPubMed Google Scholar * Yu-ichiro Matsushita View author publications You can

also search for this author inPubMed Google Scholar CONTRIBUTIONS H.N. and Y.M. conceived the general idea. H.N. modified the code provided in prior work. H.N. and T.K. developed the code

for noisy simulation. Numerical simulations were performed by H.N. All authors contributed equally to the manuscript preparation and presentation of results. CORRESPONDING AUTHOR

Correspondence to Hirofumi Nishi. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral

with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION RIGHTS AND PERMISSIONS OPEN ACCESS This article is

licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give

appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in

this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative

Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a

copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Nishi, H., Kosugi, T. & Matsushita, Yi.

Implementation of quantum imaginary-time evolution method on NISQ devices by introducing nonlocal approximation. _npj Quantum Inf_ 7, 85 (2021). https://doi.org/10.1038/s41534-021-00409-y

Download citation * Received: 03 June 2020 * Accepted: 14 April 2021 * Published: 01 June 2021 * DOI: https://doi.org/10.1038/s41534-021-00409-y SHARE THIS ARTICLE Anyone you share the

following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer

Nature SharedIt content-sharing initiative