The role of decomposition reactions in assessing first-principles predictions of solid stability

The performance of density functional theory approximations for predicting materials thermodynamics is typically assessed by comparing calculated and experimentally determined enthalpies of

formation from elemental phases, ΔHf. However, a compound competes thermodynamically with both other compounds and their constituent elemental forms, and thus, the enthalpies of the

decomposition reactions to these competing phases, ΔHd, determine thermodynamic stability. We evaluated the phase diagrams for 56,791 compounds to classify decomposition reactions into three

types: 1. those that produce elemental phases, 2. those that produce compounds, and 3. those that produce both. This analysis shows that the decomposition into elemental forms is rarely the

competing reaction that determines compound stability and that approximately two-thirds of decomposition reactions involve no elemental phases. Using experimentally reported formation

enthalpies for 1012 solid compounds, we assess the accuracy of the generalized gradient approximation (GGA) (PBE) and meta-GGA (SCAN) density functionals for predicting compound stability.

For 646 decomposition reactions that are not trivially the formation reaction, PBE (mean absolute difference between theory and experiment (MAD) = 70 meV/atom) and SCAN (MAD = 59 meV/atom)

perform similarly, and commonly employed correction schemes using fitted elemental reference energies make only a negligible improvement (~2 meV/atom). Furthermore, for 231 reactions

involving only compounds (Type 2), the agreement between SCAN, PBE, and experiment is within ~35 meV/atom and is thus comparable to the magnitude of experimental uncertainty.

The design and discovery of new materials are being rapidly accelerated by the growing availability of density functional theory (DFT) calculated property data in open materials databases,

which allows users to systematically retrieve computed results for experimentally known and yet-to-be-realized solid compounds.1,2,3,4,5 The primary properties of interest are the optimized

structure and corresponding total energy, E, with, for example, ~50,000,000 compiled structures and energies available via the NOMAD repository.6 Given E for a set of structures, one can

routinely obtain the reaction energy, Erxn, to convert between structures. E for a compound is typically compared with E for its constituent elements to obtain the formation enthalpy, ΔHf,

which provides the thermodynamic driving force at zero temperature and pressure for stability of a given structure with respect to its constituent elements:

where E is the calculated total energy of the compound (Aα1Bα2…), αi the stoichiometric coefficient of element i in the compound, and Ei the total energy (chemical potential) of element i.

ΔHf computed by Equation 1 is typically compared to ΔHf obtained experimentally at 298 K with varying degrees of agreement depending on the density functional and compounds (chemistries)

under investigation.2,3,7,8,9,10,11,12

However, ΔHf is rarely the useful quantity for evaluating the stability of a compound. The reaction energy for a given compound relative to all other compounds within the same composition

space is a more relevant metric for accessing stability, where the reaction with the most positive Erxn is the decomposition reaction.10,13,14 For example, for a given ternary compound, ABC,

the relevant space of competing materials includes the elements (A, B, and C), all binary compounds in the A–B, A–C, and B–C spaces, and all ternary compounds in the A–B–C space. The

stability of ABC is obtained by comparing the energy of ABC with that of the linear combination of competing compounds with the same average composition as ABC that minimizes the combined

energy of the competing compounds, EA–B–C. The decomposition enthalpy, ΔHd, is then obtained by:

ΔHd > 0 indicates an endothermic reaction for a given compound ABC forming from the space of competing compounds, A–B–C; the sign notation that ΔHd > 0 indicates instability is chosen to be

commensurate with the commonly reported quantity, “energy above the hull”, where ΔHd also provides the energy with respect to the convex hull but can be positive (for unstable compounds) or

negative (for stable compounds). A ternary example was shown for simplicity, but the decomposition reaction and ΔHd can be obtained for any arbitrary compound comprised of N elements by

solving the N-dimensional convex hull problem.

For the high-throughput screening of new materials for a target application, stability against all competing compounds is an essential requirement for determining the viability of a

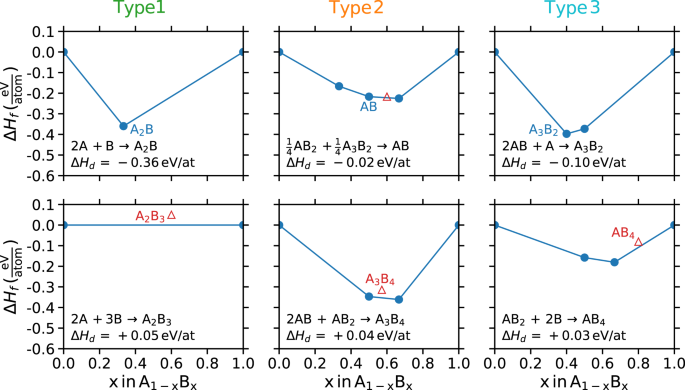
candidate material.14 In this approach, compounds are typically retained for further evaluation (more rigorous calculations or experiments) if ΔHd  0, Fig. 1, bottom).

Three unique decomposition reactions A stable (top) and metastable (bottom) example of each reaction type. Left: reaction Type 1—the decomposition products are the elements; center: reaction

Type 2—the decomposition products contain no elements; right: reaction Type 3—the decomposition products contain elements and compounds. Solid blue circles are breaks in the hull (stable)

and open red triangles are above the hull (metastable). In all examples, A and B are arbitrary elements. We note that in the stable Type 2 example (top center), the stability of AB is

determined by a stable compound, AB2, and an unstable compound, A3B2. This particular phase diagram is chosen to emphasize that the decomposition of stable compounds can include unstable

compounds

As it pertains to thermodynamic control of synthesis, Type 2 reactions are insensitive to adjustments in elemental chemical potentials that are sometimes modulated by sputtering, partial

pressure adjustments, or plasma cracking. Any changes to the elemental energies will affect the decomposition products and the compound of interest proportionally, and therefore, while ΔHf

for all compounds will change, ΔHd will be fixed. This is in contrast to Type 1 reactions which become more favorable with increases in the chemical potential of either element. The

thermodynamics of Type 3 reactions can be modulated by these synthesis approaches if the elemental form of the species whose chemical potential is being adjusted participates in the

decomposition reaction, i.e., the compound must be the nearest (within the convex hull construction) stable, or lowest energy metastable, compound to the element whose chemical potential is

being adjusted.21,22

The relative prevalence of each decomposition pathway is not yet known, although the phase diagrams of most inorganic crystals can be resolved using open materials databases. At present, the

Materials Project1 provides 56,791 unique inorganic crystalline solid compounds with computed ΔHf. Using the N-dimensional convex hull construction, we determined ΔHd and the

stability-relevant decomposition reaction for each compound and report the prevalence of each reaction type in Fig. 2. For these 56,791 compounds, Type 2 decompositions are found to be most

prevalent (63% of compounds) followed by Type 3 (34%) and Type 1 (3%) decompositions. Notably, 81% of Type 1 reactions (for which ΔHd = ΔHf) are for binary compounds, which comprise only 13%

of compounds tabulated in Materials Project. In contrast,  2 (2 elements are relevant in the decomposition reactions of 42% of 28,884 ternary compounds and 91% of 14,123 quaternary

compounds. For these cases, Efbinaries does not equal ΔHd. As a demonstration of the magnitude of this disagreement, we selected four quaternary garnet oxides (C3A2D3O12) in our dataset (A =

 Al, D = Si, C = Ca/Mg/Mn/Fe) and found that Efbinaries overestimates stability (is more negative than ΔHd) by 69 meV/atom on average (see Supplementary Information for more details). In

Figs. 4–5, our results show excellent agreement between experiment and theory for ΔHd of a diverse set of materials, considering all possible decomposition products and without requiring a

Hubbard U correction. Because Type 2 decomposition reactions only involve compounds, computing the decomposition reaction energy using total energies or formation enthalpies is

equivalent—therefore the results with (Fig. 4b) and without (Fig. 4a) fitted reference energies are identical.

Elemental energies are included in the calculation of ΔHd for compounds that compete thermodynamically with both compounds and elements (Type 3 decomposition reactions). However, for 415

reactions of this type and using either SCAN or PBE we found that the use of fitted reference energies does not significantly affect the agreement with experiment for ΔHd with improvements

of only ~2 meV/atom (Fig. 5). For these compounds, SCAN improves upon PBE by ~20% and the MAD between SCAN and experiment (73 meV/atom) falls between those for Type 1 (88 meV/atom) and Type

2 (34 meV/atom) reactions.

The prevalence of each reaction type was quantified for the Materials Project database, with Type 2 reactions accounting for 63% of all decompositions evaluated and this fraction increasing

from 29 to 67 to 75% for binary, ternary, and quaternary compounds, respectively. For these cases, our results show that both SCAN and PBE can be expected to yield chemically accurate

predictions of ΔHd, which quantifies the driving force for thermodynamic stability. While on average, SCAN and PBE perform similarly for ΔHd, this analysis is performed only on ground-state

structures within each functional. It was recently shown that SCAN performs significantly better than PBE for structure selection—i.e., identifying the correct polymorph ordering of which

crystal structure is the lowest energy at fixed composition.27 Here, ~10% of the 2238 structures optimized were found to have different space groups using PBE and SCAN. Considering only

ground-states, the lowest energy PBE and SCAN structures differ for ~11% of the 1012 unique compositions assessed in this work. While the MAD from experiment for ΔHd calculated by SCAN and

PBE differs by only ~20%, additional advantages are likely associated with the use of SCAN for the accurate description of structure and properties.25,26,27,36 The discrepancies between the

structures and polymorph energy orderings predicted by PBE and SCAN with experiment may also contribute to the reported differences between the approaches.

For 1012 compounds, we show that fitting elemental reference energies for both GGA (PBE) and meta-GGA (SCAN) density functionals improves computed formation enthalpies, ΔHf (Fig. 3).

However, to accurately predict the stability of materials, it is essential to accurately compute the decomposition enthalpy, ΔHd, which dictates stability with respect to all compounds and

elements in a given chemical space. ΔHd is computed by determining the stoichiometric decomposition reaction with the most positive reaction energy. ΔHf is only relevant for the stability of

compounds that undergo Type 1 decompositions, where the compound only competes with elemental phases and consequently, ΔHd = ΔHf. Furthermore, Type 1 decompositions occur for only 17% of

binaries and almost never (