Optical spectra of silver clusters and nanoparticles from 4 to 923 atoms from the tddft+u method

ABSTRACT The localized surface-plasmon resonances of coinage-metal clusters and nanoparticles enable many applications, the conception and necessary optimization of which require precise

theoretical description and understanding. However, for the size range from few-atom clusters through nanoparticles of a few nanometers, where quantum effects and atomistic structure play a

significant role, none of the methods employed previously has been able to provide high-quality spectra for all sizes. The main problem is the description of the filled shells of d electrons

which influence the optical response decisively. We show that the DFT+_U_ method, employed with real-time time-dependent density-functional theory calculations (RT-TDDFT), provides spectra

in good agreement with experiment for silver clusters ranging from 4 to 923 atoms, the latter representing a nanoparticle of 3 nm. Both the electron-hole-type discrete spectra of the

smallest clusters and the broad plasmon resonances of the larger sizes are obtained. All calculations use the value of the effective _U_ parameter that provides good results in bulk silver.

The agreement with experiment for all sizes shows that the _U_ parameter is surprisingly transferable. Our results open the pathway for calculations of many practically relevant systems

including clusters coupled to bio-molecules or to other nano-objects. SIMILAR CONTENT BEING VIEWED BY OTHERS TOWARDS AUTOMATION OF THE POLYOL PROCESS FOR THE SYNTHESIS OF SILVER

NANOPARTICLES Article Open access 06 April 2022 ELECTROSTATIC POTENTIALS OF ATOMIC NANOSTRUCTURES AT METAL SURFACES QUANTIFIED BY SCANNING QUANTUM DOT MICROSCOPY Article Open access 13 March

2024 STRUCTURAL TRENDS IN ATOMIC NUCLEI FROM LASER SPECTROSCOPY OF TIN Article Open access 08 June 2020 INTRODUCTION Noble-metal clusters and nanoparticles are employed in an overwhelming

number of applications and research domains1,2,3,4,5. In particular, there is enormous interest in their optical properties, mostly connected to the localized surface-plasmon resonances

(LSPRs) and their tuning and application, which creates a natural link to the field of nanoplasmonics and quantum plasmonics6,7,8. The coupling of metal clusters with, for example, organic

molecules, the exploitation of field enhancements between clusters9 or around edges and tips10 as in surface-enhanced Raman spectroscopy11, and the applications of the clusters as sensors12

call for a predictive and very precise theoretical description. However, a longstanding problem has been exactly the precise description of the coinage-metal clusters’ optical spectra and

surface-plasmon resonance energies, necessary in order to model and analyze the interaction for instance with biomolecules. Any description of such interactions clearly needs to take into

account all the quantum effects at play as well as the effects of the atomic structure and of chemical bonds present in the systems. The well-known principal problem for the coinage metals

is the proper description of the filled d shell of electrons. Interband transitions from the d electrons into states above the Fermi energy appear in the spectra of bulk silver at about 4

eV, and of gold at about 2 eV13. In addition, in the presence of a LSPR, the d electrons are polarized inside the material by the field created by the collective oscillation of the

delocalized electrons, opposing the latter14,15,16,17,18. This leads to a screening which shifts the LSPR energy to lower energies16. The opposite polarizations are easily seen in the

induced densities at the plasmon energy17,18. The d electrons are strongly localized around the atom cores, unlike the delocalized s electrons that produce the spill-out over the classical

particle radius that produces a red-shift of LSPR energies19,20,21. This leads to the concept of a layer of reduced screening of the d electrons at the surface of the clusters. The interplay

of these two effects determines the size-dependence of LSPR energies of clusters in vacuum16,22,23. For large nanostructures, purely classical approaches do well24,25,26 (Mie theory in the

case of spherical nanoparticles). For smaller particles, hydrodynamic27 and other non-local classical approaches28 have tried to include at least part of the relevant surface and quantum

effects with some success. To include quantum effects for intermediate sizes, jellium-based calculations of Time-Dependent Density-Functional Theory (TDDFT) obtain excellent results for,

e.g., the size dependence of LSPR energies, but at the price of ignoring atomistic structure and interfacial details16,23. The smallest clusters, however, are clearly quantum systems with

discrete electronic states which necessitate a full atomistic quantum description. Early on, very small clusters have been described by quantum-chemistry methods like the equation-of-motion

coupled-cluster approach29. Today, TDDFT (using pseudopotentials or similar descriptions of the electron–ion interaction) has become the workhorse of calculations on clusters, but it hasn’t

achieved, until now, the predictive quality over the full size range of clusters and nanoparticles that is needed. In particular, the approximations involved in the description of exchange

and correlation effects (functionals and kernels), might be well adapted to strongly localized systems where short-range effects play an important role, or else to more extended systems

where long-range interactions are important30,31. Over the full size range interesting for the clusters and nanoparticles, we have both regimes, which in addition might be combined in the

same system, as in the case of active tips and edges of a cluster, of tiny clusters attached to larger NPs, or in the interaction of nanoparticles with molecules. For small silver clusters,

the importance of long-range exchange effects has been shown32, and range-separated hybrid functionals provide spectra in excellent agreement with experiment33,34. However, these

calculations are numerically cumbersome and today limited to sizes of up to  ≈ 150... 200 atoms34,35. In addition, the published results for one of the largest attainable clusters (Ag147)

seem to overestimate the LSPR energy with respect to available experiment (Ref. 34, cf. Fig. 3). For larger clusters, local and semilocal functionals like the simple local-density

approximation (LDA)36 and different generalized-gradient approximations (GGA)37,38,39 have been the most widely used approximations until now18,40,41,42,43, along with meta-GGA functionals

for larger gold clusters44 and the GLLB-SC functional (SC standing for “solids and correlation”)45,46. The latter seems to be well adapted to large clusters with a clear plasmonic resonance

but does less well for sizes below about 100 atoms47. In addition, a number of approximate schemes based on TDDFT have been developed in order to reduce the numerical effort and more easily

attain larger systems, like the DFTB48 and approximate TDDFT algorithms49. The use of the simple functionals results, in general, in the filled d shells positioned too close to the Fermi

energy and, due to the resulting overestimation of the screening of the LSPR by the d electrons, underestimates the LSPR energies18,50,51,52. What is needed is a method which selectively

improves the description of the d electrons while avoiding the costly introduction of Hartree-Fock exchange as in the hybrid functionals. This can be achieved by the DFT+_U_ method as

introduced by Anisimov, Liechtenstein, and coworkers53,54,55,56 which corrects DFT calculations for problems mostly related to the over-delocalization of the d electrons, resulting from the

self-interaction problem that follows from the incomplete cancellation of the Coulombic terms when approximate density functionals are used. It has been demonstrated that for bulk metals,

the DFT+_U_ approach provides good dielectric functions that have then been used in classical calculations of the optical response of large nanoparticles57. However, this approach raises the

usual questions of transferability and of the validity of the very concept of the dielectric function for small clusters. Coviello et al. have recently extended this approach to magnetic

elements58. Explicit DFT+_U_ calculations do not seem to have been published for noble-metal clusters. In the present work, we use the DFT+_U_ approach53,54,55,56 and its extension

time-dependent DFT+_U_ (TDDFT+_U_) to obtain spectra of silver clusters in good agreement with available experiments over the full size range spanning from few-atom clusters like Ag4 through

nanoparticles of about 1000 atoms (Ag923 with more than 10,000 active electrons, about 3 nm in diameter, presently certainly inaccessible for calculations with hybrid functionals). In

particular, this includes the discrete electron–hole-type spectral features of the smallest clusters as well as the plasmonic response of larger ones, including the LSPR’s complex size

dependence and the oscillation-like behavior of small clusters due to shell-closing effects— even though significant differences between different measurements exist, notably between

low-temperature rare-gas-embedded clusters and gas phase measurements, which complicates the comparison and limits its precision. The calculated results are obtained using the same value of

the effective _U_ for all sizes, showing surprising transferability of this parameter. The numerical effort of the DFT+_U_ method is only slightly higher than that of the comparable pure DFT

calculations. Our results demonstrate that DFT+_U_ is an efficient and transferable method to model the electronic response of Ag clusters which will enable precise, predictive TDDFT

calculations of many clusters, cluster+molecule hybrid systems, and cluster-assembled materials. RESULTS AND DISCUSSION The DFT+_U_ method corrects DFT calculations for problems mostly

related to the over-delocalization of the d electrons, arising from the self-interaction errors due to the incomplete cancellation of the Coulombic terms when approximate density functionals

are used. The main effect when applying the correction to the filled d states in silver is their downward shift with respect to the Fermi level and their increased localization. In the

present work, we apply the DFT+_U_ method in its rotationally invariant formulation59 using the octopus code60, where the pseudo-wavefunctions serve as localized basis. DFT+_U_ is used for

the ground-state calculations and in the subsequent time-evolution (real-time, RT)61 TDDFT+_U_ calculations, carried out to obtain the optical spectra60. We use a constant value of the

effective _U_ of 4.0 eV. This choice was motivated by the findings of Avakyan et al., who obtained a good agreement with the experimental dielectric function of bulk silver using this

value57. We consider a range of clusters and nanoparticles representative of the clusters studied in the available literature. It comprises (i) small to medium-sized clusters, the optimized

structures of which correspond to the geometries used in Refs. 33 and 34 in order to ensure meaningful comparison with the previous calculations. These structures correspond mostly to those

found by Chen et al.62 and are, presumably, the lowest-energy structures of their respective sizes. Furthermore, we consider icosahedral structures as found in many experiments. In

particular, the icosahedral structure has been found to be the most stable geometry for the Ag55 cluster63. These icosahedral clusters are nearly spherical and particularly popular in

theoretical studies because they allow for a series of sizes (13, 55, 147, 309, 561, 923... atoms) without any change of symmetry or morphology, and there are no questions as to how to cut

the clusters out of the bulk fcc lattice (facets...) Nonetheless, while small icosahedra are both expected and also found in experiments63, the five-fold symmetries cannot exist in the bulk

material and the icosahedra become more and more strained with size. This induces a crossover64, where larger clusters exhibit a preference for fcc-based structures. Consequently, in

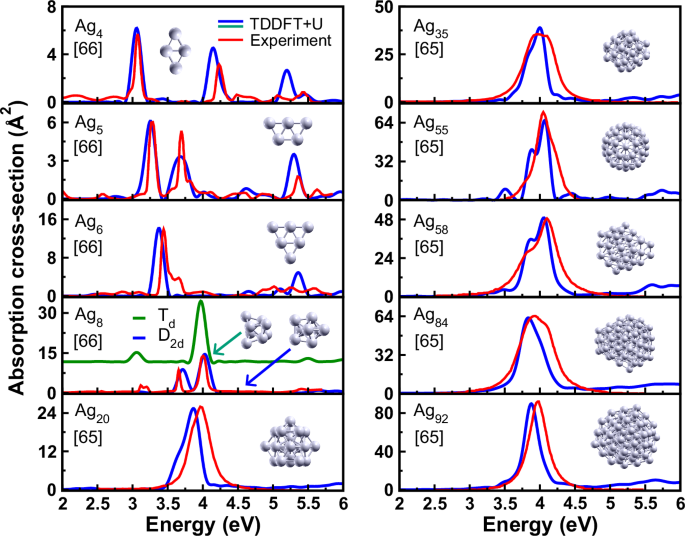
addition to the icosahedra, we consider a number of nearly spherical fcc-based clusters, i.e., clusters cut out of the fcc bulk lattice. The calculated results are shown in Figs. 1, 2, 3

along with available experimental results. The experimental spectra of the smaller, mostly non-spherical clusters shown in Fig. 1 have been obtained in different experiments on size-selected

clusters in rare-gas matrices at low temperatures. They have been taken directly from Refs. 65 and 66, and they contain an experimental intricacy: the respective rare-gas matrices are

generally assumed to induce a dielectric red-shift of the spectra, which means in turn that in order to compare between experiments in different rare gases or with clusters in vacuum, these

shifts must be corrected. The details of these shifts have been diversely discussed in the literature in the past66,67,68,69. For instance, while for the intermediate sizes between 20 and

100 atoms, shifts of around 0.17 eV for Ne and 0.29 eV for Ar have been suggested and applied by different authors, they do not seem to apply for the smallest clusters65,69,70. Our work does

not intend to resolve this issue, but we provide in the supplementary information section 1 a more extensive discussion of the subject and on the question as to how it impacts the

comparison with our calculated data. We show, in particular, that on the energy scale of Fig. 1, the good agreement does not depend on the details of these shifts. The spectra of the

smallest clusters in Fig. 1 contain multiple peaks mostly reflecting electron–hole-type excitations. The agreement of the calculations with these spectra is very good, the multiple peaks (at

least below 5 eV) are well reproduced. Starting from about 20 atoms all the way up to 92 atoms, a clear broad LSPR band arises in the absorption spectra, with peak energies lying within the

range of 3.80 and 4.01 eV. However, we have not yet entered the scalable size range, as the size-dependence is not yet smooth and monotonous. Deviations from a smooth size-dependence

originate from electronic or atomic shell-closings as discussed below, as well as from deviations of the clusters from spherical symmetry. Such deviations give rise to both energy shifts and

the occurrence of additional peaks and shoulders in the spectra. This is similar to the aspect-ratio dependence in elongated particles, which has been described classically already by Gans

in his seminal papers in 1912 and 191571,72. More recently, the behavior of small nano-rods has been studied using TDDFT73,74; a discussion distinguishing classical and quantum-mechanical

effects can be found in ref. 28. The effect on the small clusters is exemplified for the case of Ag58 in the supplementary information, supplementary Fig. S7. The geometry of the cluster

corresponds to the icosahedral Ag55 structure, with three more atoms bonded to the same facet62. While the Ag55 structure is very close to spherical, Ag58 presents an elongated cluster,

which leads to different resonance energies along the three different directions75,76 and, in turn, to additional peaks or shoulders in the spectra. This can be seen very clearly in both the

calculated and the measured spectrum of Ag58. Broadening effects can then determine how clearly the different peaks are visible in the overall spectrum. For the spectra of these small and

medium-sized clusters, the agreement between experiment and calculation is good, the remaining differences are of the order of 0.1 eV (cf. the discussion in the SI). The comparison with

previous calculations is shown in the supplementary Figs. S4,S5. The spectra of the icosahedral and of the fcc-based larger clusters are shown in Fig. 2. These larger clusters all show the

expected broad, smooth LSPR band. In the case of the icosahedral clusters, the size dependence of the LSPR energy is clearly monotonous, which is not the case for the fcc-based structures.

We note that for the size of around 300 atoms, the spectrum of the 314-atom fcc cluster is in very close agreement with the measured gas-phase spectrum of Hövel et al.77 (see inset of Fig. 

2), whereas the icosahedral cluster of essentially the same size, 309 atoms, has higher energy. In general, all the fcc-based clusters that we considered were found to have LSPR energies

lower than the icosahedral ones. A direct comparison of the calculated spectra between icosahedral and fcc-based clusters of similar sizes is provided in the supplementary information (see

supplementary Fig. S9). In this comparison, the fcc-based structures are approximately 0.1 eV lower in energy. For the size of about 150 atoms, this difference had already been pointed out

previously but not further discussed51, and it is consistent with the classical calculations of Ref. 78. In Fig. 3, we show the LSPR energies as a function of inverse radius for the clusters

which have an identifiable LSPR. This permits an overview of the different results and clearly brings out the size-dependence of the plasmons. The experimental results are measured in two

different types of experiments: in gas-phase (free-beam) experiments or on clusters embedded in rare-gas matrices as described above. The two types of experiments are consistent among

themselves but differ from each other: the free-beam energies lie consistently below the shifted measurements on the rare-gas-embedded clusters, which renews the questions about the

matrix-induced shifts. In particular, it demonstrates immediately the problem in the comparison of our calculated energies with the experimental points that have been obtained using the two

types of measurements. For that reason, we present the results of the rare-gas-embedded clusters in Fig. 3 by the shaded bands ranging from the shifted results to the unshifted (as measured)

results. The measurements of clusters in free-beam experiments do not contain the type of matrix-induced shifts as mentioned above for the clusters in rare-gas matrices. However, a number

of effects are expected to lead to small red-shifts compared to the situation described in the calculations. We discuss these effects in the supplementary information section 2. The

calculated results of the fcc clusters and the small clusters lie close to or slightly above (up to about 0.2 eV) the band defined by the different free-beam results. If the TDDFT+_U_

results are correct, this is precisely what one would expect because a number of effects lead to small red-shifts in the free-beam experiment compared to the ideal situation of the

calculations. These effects include size-distributions, temperature, negative charges, and the presence of a surrounding helium droplet in some cases79. They are discussed in detail in

supplementary information section 2. By contrast, the series of icosahedral clusters produces higher energies. The difference with respect to the fcc clusters is interesting, in particular

because the icosahedra have then been used in a large variety of theoretical studies by many groups, see for instance refs. 36,41,47,51,80,81,82. Below about 100 atoms, we enter the

non-scalable size regime where each atom counts and shell closings influence the size dependence strongly, as clearly seen in the measurements of Harbich et al. and Fedrigo et al.68,83. This

effect is apparent in our calculations involving the lowest-energy structures, shown by the black crosses connected with black dashed lines. In addition to the points extracted from the

spectra shown in Fig. 1, further calculations were performed, their spectra are provided in the SI (see supplementary Fig. S2). Clearly, the three structures Ag18, Ag34 and Ag92 where

closed-shell configurations are expected show maximum values of the plasmon energy vs. inverse size. Somewhat exceptionally, the plasmon of Ag58, which also has a closed-shell electronic

configuration (cf. supplementary Fig. S8), was found to be slightly lower in energy than that of the highly symmetric Ag55 cluster, which can be attributed at least in part to its elongated

shape (see supplementary Fig. S7). In addition, this is a case where the electronic shell closing and the structural shell closing (at 55 atoms) interfere with each other. This effect has

already been mentioned in Ref. 65. We note that the absolute energies do not coincide particularly well with the shifted published results of the rare-gas-embedded clusters on the very fine

energy scale of Fig. 3—our calculated energies lie within the band defined by the shifted and the unshifted energies, with differences of up to 0.2 eV. However, the variations, with their

maxima determined by the shell-closings, are well reproduced. In other words, while the question of the absolute values of the plasmon energies and the treatment of the matrix-related shifts

remains, our calculations reproduce the effect of the shell-closings on the plasmon energies well. ON THE VALUE OF THE EFFECTIVE _U_ PARAMETER For the effective _U_ parameter, we have used

the value of 4 eV in all the calculations presented up to here, thus tacitly assuming that it can be used for all sizes. In view of the above-mentioned difficulties in the comparison with

the experimental plasmon energies, this assumption needs to be critically assessed. To study the effect of a varying effective _U_, we re-calculated the spectra with different effective _U_

values for the two smallest icosahedral clusters considered in this work (see supplementary Figs. S10,S11) and for some of the smallest clusters (supplementary Fig. S12). We found that to

match the range defined by the free-beam experiments for the icosahedral clusters, effective _U_ values of  ~2.5 eV and  ~1.0 eV would be needed for Ag147 and Ag55, respectively. However,

such a decrease of _U_ with decreasing size would produce immediate contradictions: the decrease of _U_ would strongly degrade the comparison with experiment for the smallest clusters as

shown in Supplementary Fig. S12 (assuming that no strong jumps occur in the hypothetical size-dependence of _U_). In addition, it would likewise drastically deteriorate the comparison with

the high-level calculations for the small clusters by Rabilloud et al.32 using range-separated hybrid functionals. Finally, it would mean that now the fcc-based clusters would have plasmon

energies well below the range defined by the free-beam experiments. However, as it is unlikely that the icosahedral clusters are the most representative for the measured clusters as

discussed above, that would degrade the overall comparison with experiment, keeping in mind that our calculated results should be at, or slightly above, the measured plasmon energies. Hence,

the fixed value of _U_ = 4 eV appears to be well adapted, and any residual size dependence of _U_ is expected to be weak. This, in turn, is an important result in its own right because it

demonstrates a surprising transferability of _U_: the value determined for bulk silver can be used for all cluster sizes. In addition, a self-consistent determination of the _U_ parameter

adapted finely to different situations and also to the different atoms in a given system would be desirable. We undertook such calculations using the ACBN0 functional implemented in the

octopus code, but they were unsuccessful and returned unphysical results for unknown reasons. The resolution of this problem is certainly an avenue for future research. COMPARISON WITH

PREVIOUS CALCULATIONS For larger clusters, as mentioned above, local and semilocal functionals like the simple local-density approximation (LDA), cf. Ref. 36, and different

generalized-gradient approximations (GGA) like the PBE functional37, the Wu-Cohen38 functional, and the asymptotically corrected LB94 functional39 have been the most widely used

approximations until now18,40,41,42,43. The meta-GGA functional VS98 has been used for larger gold clusters44. The use of the local and semilocal functionals results, in general, in the

filled d shells being positioned too close to the Fermi energy and, due to the resulting overestimation of d screening of the LSPR, underestimates LSPR energies (see supplementary Fig. 

S3)18,51,52. For larger clusters, Kuisma et al. have employed the Gritsenko-van Leeuwen-van Lenthe-Baerends solid-correlation potential (GLLB-SC)45,46 (see supplementary Fig. S5). Their

results47 are only slightly higher than ours for the larger clusters, but the quality of these results seems to degrade strongly with decreasing size: there is a clear overestimate of the

LSPR in Ag55 with respect to all available experimental results shown in Fig. 3. For small clusters, excellent results have been obtained using the numerically costly range-separated hybrid

functionals32,34 (see supplementary Fig. S4). In general, the quality of our spectra is comparable with those results. However, interestingly, the largest cluster that seems to have been

published using this method, Ag147, has an LSPR energy that is distinctly higher than that obtained with TDDFT+_U_, and in view of Fig. 3 it seems decidedly too high compared to all

available experiments. In addition, the calculations using the range-separated hybrid functionals would not be feasible with today’s numerical means for the larger clusters, beyond maybe 200

silver atoms. In comparison with these calculations, only the TDDFT+_U_ method yields reliable spectra over the full treatable size range, from the smallest clusters to the 3 nm

nanoparticle of 923 atoms. EFFECT OF _U_ CORRECTION ON LOCALIZATION AND DENSITY OF STATES While the spectra shown and discussed above are the central result of our present work, we need to

analyze the effect of the _U_ correction on other observables as well in order to obtain a full understanding of our results. In particular, the redistribution of the total electronic

density is shown in Fig. 4, presented as the difference between the total charge density of the Ag4 cluster calculated using GGA (PBE) with the inclusion of the Hubbard correction of 4 eV

and GGA (PBE) without the correction. This difference is illustrated using an iso-surface plot and a color-coded slab passing through the plane defined by the four Ag atoms in the cluster,

showing regions of electron density increase and decrease in red and blue, respectively. The red region exhibits the characteristic shape of the d orbitals, visually confirming the enhanced

localization of the 4d electrons upon applying the _U_ correction term. Additionally, the Hubbard _U_ correction shifts the 4d states to lower energies with respect to the Fermi energy, as

it is evident in the projected density of states (PDOS) of the Ag309 cluster, shown in Fig. 4b. The correction in the energetic position of the 4d states ensures that the threshold of the

interband transitions from the occupied 4d states into higher unoccupied states beyond the Fermi energy appears at the correct energy. A comparison with experimental photoemission spectra in

supplementary Fig. S6 shows that the d-band edge is well corrected, even though the width of the d band is somewhat overestimated. The latter point does not, however, impact the calculation

of the spectra and plasmon energies strongly, as is evidenced by the results shown above. In addition, our calculation captures all the important features of the occupied states above the d

band present in the UV photoemission spectra of Ag55. This shows that, as expected, the main effect of the inclusion of the _U_ correction is to correct the principal shortcoming of the

simple functionals—namely, the incorrect description of the localized d states, with the d band lying too close to the Fermi energy and the interband transitions appearing too low in the

spectra, thereby interfering unphysically with the LSPR and overestimating the screening of it15,16,18. Thus the correction in turn significantly improves the agreement with experimental

optical spectra as shown above. To quantify the localization effect of the d orbitals, we calculated the average occupation of the d orbitals for clusters of all sizes with and without the

Hubbard _U_ correction. Our analysis found that the average occupation of the d orbitals in DFT+_U_ calculations was higher in comparison to the calculations without _U_ correction, implying

enhanced d-electron localization in agreement with the results shown in Fig. 4. Additionally, we observe an increase in the average occupation of the d orbitals with decreasing cluster

size. To gain a deeper understanding of how the different atomic sites contribute towards the average localization of the 4d electrons, we analyzed the average occupation of the 4d orbitals

shell-wise in the five icosahedral structures, which is shown in Fig. 5b. It is evident from the figure that the d electrons are more localized in the atoms of the two outermost shells than

inside in all cases. Below the two outermost layers, the localization is roughly constant. This means that the increase in average localization in Fig. 5a is due to the increasing

surface-to-volume ratio as size decreases. All these results are coherent with our general understanding of the d screening of the LSPR. An increase of the localization implies a reduction

of the polarizability of the d electrons, thereby reducing their screening effect as discussed above. The increased average localization in DFT+_U_ thus provides a contribution to the blue

shift of the plasmon compared to GGA (PBE). The increase of average localization with decreasing cluster size and the resulting decrease of the average d screening in both DFT and DFT+_U_ 

are consistent with the observed blue shift in the LSPR. It is interesting to note that the increased localization of the outermost atoms’ d states, which implies their decreased

polarizability and, hence, a decreased contribution to the overall screening at the surface, points in the same direction as the above-mentioned effect of the surface layer of reduced d

screening due to the spatial localization of the d electrons around the atom cores. This is even more relevant as it is known that the outermost atomic shell plays an important role in the

determination of the optical properties80. The model of a reduced screening layer generally applied in many jellium calculations14,23,84 is, therefore, an effective model that is able to

represent both the localization of the d electrons at a short distance from the surface and the increased localization around each atom in the surface layer. CONCLUSION In conclusion, the

TDDFT+_U_ method provides optical spectra over the full-size range from few-atom silver clusters to nanoparticles of about 3 nm in diameter, corresponding to about one thousand atoms and

containing  ≈10,000 active electrons. In addition to the electron–hole-type transitions of small clusters, our calculations obtain the broad plasmon resonances of the larger spherical

clusters and their size dependence. The numerical effort is only slightly larger than that of pure TDDFT calculations. Precise comparison with experiment is complicated by inconsistencies in

the experimental literature and uncertainties about the cluster structures. Our results for small clusters up to about 100 atoms reproduce the spectra measured on rare-gas-embedded clusters

very well, including in particular the spectra with multiple peaks. Their calculated plasmon energies reproduce in particular the oscillation-like behavior due to electronic shell-closing

effects, whereas comparison of the absolute energies is only possible up to remaining differences of up to about 0.2 eV due to uncertainties in the treatment of the matrix shifts needed in

the comparison. By contrast, the calculated plasmon energies of fcc-based nearly spherical clusters are in good general agreement with (i.e., close to or slightly above) the range defined by

available free-beam experiments. The series of icosahedral clusters has generally higher plasmon energies. The TDDFT+_U_ approach is the only method that, at this time, achieves this degree

of agreement with experiment over the full-size range because the costly range-separated hybrid functionals cannot realize calculations of clusters beyond ≈ 200 atoms, and the

solid-state-derived meta-GGA calculations that fare well for large clusters seem to fare poorly below about 100 atoms. The value of the effective _U_ turns out to be surprisingly

transferable for the silver clusters. The same value of 4 eV that had produced spectra in good agreement with the experiment for bulk silver was used without any adaptation for all the

clusters in the present work, including the smallest one, Ag4. Tests with different _U_ values strongly suggest that any residual size-dependent variation of _U_ will be weak. To use the

full power of the TDDFT+_U_ method, a more precise comparison with the experiment would be desirable. We hope that our work can motivate further experimental investigations that will

consolidate the available results and, in particular, help settle the open questions about cluster-matrix interactions and the resulting shifts. Clearly, the TDDFT+_U_ method can likewise be

used to calculate systems where the clusters are coupled to each other or to bio-molecules, DNA strands, etc. Our results open the pathway to direct TDDFT+_U_ calculations of many

practically relevant systems and processes, including, for instance, medical imaging applications, biomolecule labeling, sensing, and many others. METHODS EXPERIMENTAL SPECTRA AND LSPR

ENERGIES Experimental absorption spectra of the clusters with 20 to 92 Ag atoms were scanned from Ref. 34 where they include already a blue shift of 0.17 eV to compensate for the dielectric

effect of the neon matrix present in the original experiment65. The absorption spectra of the smallest clusters embedded in a neon matrix were taken directly from Ref. 66 without any matrix

correction, as it was done in previous publications32,33,66. For the plot of the LSPR energy vs. inverse radius, Fig. 3, the radius of the particle was approximated using _R_ = 

_r__s_*_N_1/3Å, with _r__s_ = 1.626 being the electronic density parameter of bulk silver and _N_ being the number of Ag atoms. The values of Charlé et al. and Harbich et al. were scanned

from Refs. 68,70,83 and consequently contain a blue-shift of 0.29 eV to compensate the dielectric shift of the Ar matrix discussed in that reference22. The data points from Yu et al.65 were

taken from the table in that reference and were blue shifted by 0.17 eV by us to compensate for the dielectric shift of the Ne matrix. The values of Refs. 79, 77, and 84 were taken directly

from the references, naturally with no shifts. For a detailed discussion of the shifts, please refer to the SI, section 1. GEOMETRIES The structures used for the calculations shown in Fig. 1

were taken from the works of Schira et al.34 and Anak et al.33. Additional structures, which were primarily used to calculate more points for the _E_LSPR-vs.-1/_R_ curve, were taken from

the work of Chen et al.62. The Ag34 structure was constructed by selectively removing one atom from the Ag35 cluster, ensuring a roughly spherical overall shape. This newly constructed

structure when fully relaxed with the VASP code was found to be only 1.3 meV/atom higher in energy than the structure for the same size provided by Chen et al. The icosahedral and fcc-based

geometries were constructed by us. For consistency, all the structures were again relaxed with the VASP code85,86, using the GGA functional as parameterized by Perdew and Wang for the

exchange and correlation87. CALCULATIONS Both the ground state and the optical absorption spectra of all structures were calculated using the DFT+_U_ method as implemented60 in the octopus

code88. Our investigation uses the rotationally invariant formulation59 of the DFT+_U_ method where _U_eff = _U_ − _J_ is used but generally referred to as just _U_. It acts locally on the

4d orbitals at all Ag atomic sites. Absorption spectra were calculated using real-time TDDFT+_U_ using the Yabana-Bertsch time-evolution formalism61, which involves real-time progagation of

the wavefunction after a delta kick at _t_ = 0. We have used the Approximated Enforced Time-Reversal Symmetry (aetrs) propagator, with a time step of ≈ 0.0016 fs (0.0024 ℏ/eV) and a total

propagation time of ≈ 26 fs (40 ℏ/eV). For the icosahedral and fcc-clusters, a shorter propagation time of ≈ 13 fs (20 ℏ/eV) was used. We use the _U_ value of 4.0 eV for all calculations.

This choice was motivated by the finding that this value provides good dielectric functions for bulk silver57. Apart from the _U_ correction, we used PBE to approximate the

exchange-correlation functional37. The interactions between the electrons and the ions were described using norm-conserving Troullier-Martins pseudopotentials89, treating 11 valence

electrons corresponding to the 10 4d electrons and one 5s electron per Ag atom explicitly. For all the spectra shown in Fig. 1, the grid spacing was set to 0.18 Å. The so-called minimum

radius, which indicates the radius of spheres around each atom, the superposition of which makes up the domain used for the calculation, was set to 7.5 Å. For the Ag147 to Ag561 icosahedral

clusters, a grid spacing of 0.20 Å and a simulation radius of 7.5 Å were used, while for Ag923, a smaller radius of 5.0 Å was employed. This is justified because the differences in the LSPR

energetic position due to the use of smaller radii decreased strongly with increasing cluster size in our tests, decreasing from 0.05 eV for Ag55 to 0.01 eV for Ag561, and thus are expected

to be negligible for Ag923. For the fcc-based clusters the spacing and the radius were set to 0.20 Å and 7.5 Å. The LSPR energies for all the structures were identified by limiting the

evolution time to  ≈ 13 fs (20 _ℏ_/eV), which is equivalent to applying a larger broadening to the spectra. The plasmon energy was then identified as the maximum of the peak. For calculating

the average localization of the d orbitals, we used the following expression $$\langle {n}_{4d}\rangle=\frac{1}{I}{\sum }_{j}^{I}\frac{{{\rm{trace}}}({n}_{m,{m}^{{\prime} }}^{j})}{5}$$ (1)

where _I_ is the total number of atomic sites, \({n}_{m,{m}^{{\prime} }}^{j}\) are the occupation matrices defined as the density matrix of a localized orbital atomic basis set {_ϕ__j_,_m_}

obtained from the pseudopotential, attached to the _j__t__h_ atomic site60. From the Kohn-Sham wavefunctions, the occupation matrix for the _j__t__h_ atom is given by $${n}_{m,{m}^{{\prime}

}}^{j}={\sum}_{n}{f}_{n}\langle {\psi }_{n}| {\phi }_{j,m}\rangle \langle {\phi }_{j,{m}^{{\prime} }}| {\psi }_{n}\rangle$$ (2) where _f_ is the occupation of the _n__t__h_ KS state and _m_

or \({m}^{{\prime} }\) are the angular quantum numbers of the localized atomic basis set, which in our case is restricted to the 4d orbitals. For calculating the shell-wise average

occupation of the d orbitals for the icosahedral structures, we used the same eq (1), taking averages over the atomic sites of one shell at a time. The first shell refers to the central atom

alone. REPORTING SUMMARY Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article. DATA AVAILABILITY Source data are provided as

a Source Data file. Additional data are available from the corresponding authors upon request. Source data are provided with this paper. REFERENCES * Schwartzberg, A. M. & Zhang, J. Z.

Novel optical properties and emerging applications of metal nanostructures. _J. Phys. Chem. C_ 112, 10323–10337 (2008). Article  CAS  Google Scholar  * Chakraborty, I. & Pradeep, T.

Atomically precise clusters of noble metals: emerging link between atoms and nanoparticles. _Chem. Rev._ 117, 8208–8271 (2017). Article  CAS  PubMed  Google Scholar  * Gilroy, K. D.,

Ruditskiy, A., Peng, H.-C., Qin, D. & Xia, Y. Bimetallic nanocrystals: syntheses, properties, and applications. _Chem. Rev._ 116, 10414–10472 (2016). Article  CAS  PubMed  Google Scholar

  * Zhang, X.-F., Liu, Z.-G., Shen, W. & Gurunathan, S. Silver nanoparticles: synthesis, characterization, properties, applications, and therapeutic approaches. _Int. J. Mol. Sci._ 17,

1534 (2016). Article  PubMed  Google Scholar  * Mathew, A. & Pradeep, T. Noble metal clusters: applications in energy, environment, and biology. _Part. Part. Syst. Charact._ 31,

1017–1053 (2014). Article  CAS  Google Scholar  * Tame, M. S. et al. Quantum plasmonics. _Nat. Phys._ 9, 329–340 (2013). Article  CAS  Google Scholar  * Marinica, D., Kazansky, A.,

Nordlander, P., Aizpurua, J. & Borisov, A. G. Quantum plasmonics: nonlinear effects in the field enhancement of a plasmonic nanoparticle dimer. _Nano Lett._ 12, 1333–1339 (2012). Article

  ADS  CAS  PubMed  Google Scholar  * Varas, A., García-González, P., Feist, J., García-Vidal, F. & Rubio, A. Quantum plasmonics: from jellium models to ab initio calculations.

_Nanophotonics_ 5, 409–426 (2016). Article  Google Scholar  * Tripathy, S. et al. Acousto-plasmonic and surface-enhanced Raman scattering properties of coupled gold nanospheres/nanodisk

trimers. _Nano Lett._ 11, 431–437 (2011). Article  ADS  CAS  PubMed  Google Scholar  * Hao, F., Nehl, C. L., Hafner, J. H. & Nordlander, P. Plasmon resonances of a gold nanostar. _Nano

Lett._ 7, 729–732 (2007). Article  ADS  CAS  PubMed  Google Scholar  * Zong, C. et al. Surface-enhanced Raman spectroscopy for bioanalysis: reliability and challenges. _Chem. Rev._ 118,

4946–4980 (2018). Article  CAS  PubMed  Google Scholar  * Mejía-Salazar, J. & Oliveira Jr, O. N. Plasmonic biosensing: focus review. _Chem. Rev._ 118, 10617–10625 (2018). Article  PubMed

  Google Scholar  * Johnson, P. B. & Christy, R. Optical constants of the noble metal. _Phys. Rev. B_ 6, 4370–4379 (1972). Article  ADS  CAS  Google Scholar  * Liebsch, A.

Surface-plasmon dispersion and size dependence of Mie resonance: silver versus simple metals. _Phys. Rev. B_ 48, 11317–11328 (1993). Article  ADS  CAS  Google Scholar  * Serra, L. &

Rubio, A. Core polarization in the optical response of metal clusters: generalized time-dependent density-functional theory. _Phys. Rev. Lett._ 78, 1428–1431 (1997). Article  ADS  CAS 

Google Scholar  * Cottancin, E. et al. Optical properties of noble metal clusters as a function of the size: comparison between experiments and a semi-quantal theory. _Theor. Chem. Acc_ 116,

514–523 (2006). Article  CAS  Google Scholar  * Weissker, H.-C. H. & López-Lozano, X. Surface plasmons in quantum-sized noble-metal clusters: TDDFT quantum calculations and the

classical picture of charge oscillations. _Phys. Chem. Chem. Phys._ 17, 28379–28386 (2015). Article  CAS  PubMed  Google Scholar  * Sinha-Roy, R., García-González, P., López-Lozano, X. &

Weissker, H.-C. H. Visualizing screening in noble-metal clusters: static vs. dynamic. _Phys. Chem. Chem. Phys._ 25, 2075–2083 (2023). Article  CAS  PubMed  Google Scholar  * Liebsch, A.

Surface plasmon dispersion of Ag. _Phys. Rev. Lett._ 71, 145–148 (1993). Article  ADS  CAS  PubMed  Google Scholar  * Kim, J.-S., Chen, L., Kesmodel, L. L., García-González, P. &

Liebsch, A. Surface plasmon dispersion of Cl/Ag(111). _Phys. Rev. B_ 56, R4402–R4405 (1997). Article  ADS  CAS  Google Scholar  * Liebsch, A. Prediction of a Ag multipole surface plasmon.

_Phys. Rev. B_ 57, 3803–3806 (1998). Article  ADS  CAS  Google Scholar  * Haberland, H. Looking from both sides. _Nature_ 494, E1–E2 (2013). Article  ADS  CAS  PubMed  Google Scholar  *

Campos, A. et al. Plasmonic quantum size effects in silver nanoparticles are dominated by interfaces and local environments. _Nat. Phys._ 15, 275–280 (2019). Article  CAS  Google Scholar  *

Jensen, T., Kelly, L., Lazarides, A. & Schatz, G. C. Electrodynamics of noble metal nanoparticles and nanoparticle clusters. _J. Clust. Sci._ 10, 295–317 (1999). Article  CAS  Google

Scholar  * Kelly, K. L., Coronado, E., Zhao, L. L. & Schatz, G. C. The optical properties of metal nanoparticles: the influence of size, shape, and dielectric environment. _J. Phys.

Chem. B_ 107, 668–677 (2003). * Maier, S. _Plasmonics: Fundamentals and Applications_ (Springer, 2007). * Christensen, T. et al. Nonlocal response of metallic nanospheres probed by light,

electrons, and atoms. _ACS Nano_ 8, 1745–1758 (2014). Article  CAS  PubMed  Google Scholar  * Sinha-Roy, R., García-González, P., Weissker, H.-C. H., Rabilloud, F. & Fernandez-Dominguez,

A. I. Classical and ab initio plasmonics meet at sub-nanometric noble metal rods. _ACS Photonics_ 4, 1484–1493 (2017). Article  CAS  Google Scholar  * Bonacic-Koutecky, V., Veyret, V. &

Mitric, R. Ab initio study of the absorption spectra of Ag_n_ (n = 5–8) clusters. _J. Chem. Phys._ 115, 10450–10460 (2001). Article  ADS  CAS  Google Scholar  * Sottile, F. et al. TDDFT

from molecules to solids: the role of long-range interactions. _Int. J. Quant. Chem._ 102, 684 (2005). Article  ADS  CAS  Google Scholar  * Weissker, H.-C. H. et al. Dynamic structure factor

and dielectric function of silicon for finite momentum transfer: Inelastic x-ray scattering experiments and ab initio calculations. _Phys. Rev. B_ 81, 085104 (2010). Article  ADS  Google

Scholar  * Rabilloud, F. Assessment of the performance of long-range-corrected density functionals for calculating the absorption spectra of silver clusters. _J. Phys. Chem. A_ 117,

4267–4278 (2013). Article  CAS  PubMed  Google Scholar  * Anak, B., Bencharif, M. & Rabilloud, F. Time-dependent density functional study of UV-visible absorption spectra of small noble

metal clusters (Cu_n_, Ag_n_, Au_n_, n = 2–9, 20). _RSC Adv._ 4, 13001–13011 (2014). Article  ADS  CAS  Google Scholar  * Schira, R. & Rabilloud, F. Localized surface plasmon resonance

in free silver nanoclusters Ag_n_, n = 20–147. _J. Phys. Chem. C_ 123, 6205–6212 (2019). Article  CAS  Google Scholar  * Seveur, P., Boubekeur-Lecaque, L., Maurel, F. & Brémond, E.

Modeling the photo-absorption properties of noble metal nanoclusters: A challenge for density-functional theory. _J. Phys. Chem. C_ 127, 7718–7729 (2023). Article  CAS  Google Scholar  *

Iida, K., Noda, M., Ishimura, K. & Nobusada, K. First-principles computational visualization of localized surface plasmon resonance in gold nanoclusters. _J. Phys. Chem. A_ 118,

11317–11322 (2014). Article  CAS  PubMed  Google Scholar  * Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. _Phys. Rev. Lett._ 77, 3865 (1996).

Article  ADS  CAS  PubMed  Google Scholar  * Wu, Z. & Cohen, R. E. More accurate generalized gradient approximation for solids. _Phys. Rev. B_ 73, 235116 (2006). Article  ADS  Google

Scholar  * Van Leeuwen, R. & Baerends, E. J. Exchange-correlation potential with correct asymptotic behavior. _Phys. Rev. A_ 49, 2421–2431 (1994). Article  ADS  Google Scholar  * Malola,

S., Lehtovaara, L., Enkovaara, J. & Häkkinen, H. Birth of the localized surface plasmon resonance in monolayer-protected gold nanoclusters. _ACS Nano_ 7, 10263–10270 (2013). Article 

CAS  PubMed  Google Scholar  * Koval, P., Marchesin, F., Foerster, D. & Sánchez-Portal, D. Optical response of silver clusters and their hollow shells from linear-response TDDFT. _J.

Phys.: Condens. Matter_ 28, 214001 (2016). ADS  PubMed  Google Scholar  * Aikens, C. M., Li, S. & Schatz, G. C. From discrete electronic states to plasmons: TDDFT optical absorption

properties of Ag_n_ (n = 10, 20, 35, 56, 84, 120) tetrahedral clusters. _J. Phys. Chem. C_ 112, 11272 (2008). Article  CAS  Google Scholar  * Burgess, R. W. & Keast, V. J. TDDFT study of

the optical absorption spectra of bare gold clusters. _J. Phys. Chem. C_ 118, 3194–3201 (2014). Article  CAS  Google Scholar  * Sakthivel, N. A. et al. The missing link: Au191(SPh- _t_Bu)66

janus nanoparticle with molecular and bulk-metal-like properties. _J. Am. Chem. Soc._ 142, 15799–15814 (2020). Article  CAS  PubMed  Google Scholar  * Kuisma, M., Ojanen, J., Enkovaara, J.

& Rantala, T. T. Kohn-Sham potential with discontinuity for band gap materials. _Phys. Rev. B_ 82, 115106 (2010). Article  ADS  Google Scholar  * Gritsenko, O., van Leeuwen, R., van

Lenthe, E. & Baerends, E. J. Self-consistent approximation to the Kohn-Sham exchange potential. _Phys. Rev. A_ 51, 1944–1954 (1995). Article  ADS  CAS  PubMed  Google Scholar  * Kuisma,

M. et al. Localized surface plasmon resonance in silver nanoparticles: atomistic first-principles time-dependent density-functional theory calculations. _Phys. Rev. B_ 91, 115431 (2015).

Article  ADS  Google Scholar  * Maghrebi, K. et al. Rapid access to ground- and excited-state properties of gold nanoclusters coated with organic ligands: evaluation of the DFTB method

performance. _J. Phys. Chem. C_ 127, 19675–19686 (2023). Article  CAS  Google Scholar  * Baseggio, O., Fronzoni, G. & Stener, M. A new time dependent density functional algorithm for

large systems and plasmons in metal clusters. _J. Chem. Phys._ 143, 024106 (2015). Article  ADS  PubMed  Google Scholar  * Rabilloud, F. Description of plasmon-like band in silver clusters:

the importance of the long-range Hartree-Fock exchange in time-dependent density-functional theory simulations. _J. Chem. Phys._ 141 (2014). * Weissker, H.-C. H. & Mottet, C. Optical

properties of pure and core-shell noble-metal nanoclusters from TDDFT: The influence of the atomic structure. _Phys. Rev. B_ 84, 165443 (2011). Article  ADS  Google Scholar  * Weissker,

H.-C. H., Whetten, R. L. & López-Lozano, X. Optical response of quantum-sized Ag and Au clusters–cage vs. compact structures and the remarkable insensitivity to compression. _Phys. Chem.

Chem. Phys._ 16, 12495–12502 (2014). Article  CAS  PubMed  Google Scholar  * Anisimov, V. I., Aryasetiawan, F. & Lichtenstein, A. I. First-principles calculations of the electronic

structure and spectra of strongly correlated systems: the LDA+U method. _J. Phys.: Condens. Matter_ 9, 767 (1997). ADS  CAS  Google Scholar  * Anisimov, V. I., Solovyev, I. V., Korotin, M.

A., Czyżyk, M. T. & Sawatzky, G. A. Density-functional theory and NiO photoemission spectra. _Phys. Rev. B_ 48, 16929–16934 (1993). Article  ADS  CAS  Google Scholar  * Liechtenstein, A.

I., Anisimov, V. I. & Zaanen, J. Density-functional theory and strong interactions: orbital ordering in Mott-Hubbard insulators. _Phys. Rev. B_ 52, R5467–R5470 (1995). Article  ADS  CAS

  Google Scholar  * Anisimov, V. I., Zaanen, J. & Andersen, O. K. Band theory and Mott insulators: Hubbard U instead of Stoner I. _Phys. Rev. B_ 44, 943–954 (1991). Article  ADS  CAS 

Google Scholar  * Avakyan, L. et al. Theoretical approach for calculation of dielectric functions of plasmonic nanoparticles of noble metals, magnesium and their alloys. _Opt. Mater._ 109,

110264 (2020). Article  CAS  Google Scholar  * Coviello, V. et al. Accurate prediction of the optical properties of nanoalloys with both plasmonic and magnetic elements. _Nat. Commun._ 15,

834 (2024). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Dudarev, S. L., Botton, G. A., Savrasov, S. Y., Humphreys, C. & Sutton, A. P. Electron-energy-loss spectra and

the structural stability of nickel oxide: An LSDA+U study. _Phys. Rev. B_ 57, 1505 (1998). Article  ADS  CAS  Google Scholar  * Tancogne-Dejean, N., Oliveira, M. J. & Rubio, A.

Self-consistent DFT+_U_ method for real-space time-dependent density functional theory calculations. _Phys. Rev. B_ 96, 245133 (2017). Article  ADS  Google Scholar  * Yabana, K. &

Bertsch, G. Time-dependent local-density approximation in real time. _Phys. Rev. B_ 54, 4484 (1996). Article  ADS  CAS  Google Scholar  * Chen, M., Dyer, J. E., Li, K. & Dixon, D. A.

Prediction of structures and atomization energies of small silver clusters, (Ag)_n_, n < 100. _J. Phys. Chem. A_ 117, 8298–8313 (2013). * Schooss, D. et al. The structures of

\({{{\rm{Ag}}}}_{55}^{+}\) and \({{{\rm{Ag}}}}_{55}^{+}\): trapped ion electron diffraction and density functional theory. _Nano Lett._ 5, 1972–1977 (2005). Article  ADS  CAS  PubMed  Google

Scholar  * Baletto, F., Ferrando, R., Fortunelli, A., Montalenti, F. & Mottet, C. Crossover among structural motifs in transition and noble-metal clusters. _J. Chem. Phys._ 116,

3856–3863 (2002). Article  ADS  CAS  Google Scholar  * Yu, C. et al. Optical properties of size selected neutral Ag clusters: electronic shell structures and the surface plasmon resonance.

_Nanoscale_ 10, 20821–20827 (2018). Article  CAS  PubMed  Google Scholar  * Lecoultre, S. et al. Ultraviolet-visible absorption of small silver clusters in neon: Ag_n_ (n = 1–9). _J. Chem.

Phys._ 134, 184504 (2011). Article  ADS  CAS  PubMed  Google Scholar  * Fedrigo, S., Harbich, W. & Buttet, J. Media effects on the optical absorption spectra of silver clusters embedded

in rare gas matrices. _Int. J. Mod. Phys. B_ 6, 3767–3771 (1992). Article  ADS  CAS  Google Scholar  * Harbich, W., Fedrigo, S. & Buttet, J. The optical absorption spectra of small

silver clusters (n = 8–39) embedded in rare gas matrices. _Z. Phys. D At. Mol. Clust._ 26, 138–140 (1993). Article  ADS  CAS  Google Scholar  * Gervais, B. et al. Simple DFT model of

clusters embedded in rare gas matrix: trapping sites and spectroscopic properties of Na embedded in Ar. _J. Chem. Phys._ 121, 8466–8480 (2004). Article  ADS  CAS  PubMed  Google Scholar  *

Charlé, K.-P., Frank, F. & Schulze, W. The optical properties of silver microcrystallites in dependence on size and the influence of the matrix environment. _Ber. Bunsenges.

Physikalische Chem._ 88, 350–354 (1984). Article  Google Scholar  * Gans, R. Über die Form ultramikroskopischer Goldteilchen. _Ann. Phys._ 342, 881–900 (1912). Article  Google Scholar  *

Gans, R. Über die Form ultramikroskopischer Silberteilchen. _Ann. Phys._ 352, 270–284 (1915). Article  Google Scholar  * López-Lozano, X., Barron, H., Mottet, C. & Weissker, H.-C. H.

Aspect-ratio- and size-dependent emergence of the surface-plasmon resonance in gold nanorods – an ab initio TDDFT study. _Phys. Chem. Chem. Phys._ 16, 1820–1823 (2014). Article  PubMed 

Google Scholar  * Johnson, H. E. & Aikens, C. M. Electronic structure and TDDFT optical absorption spectra of silver nanorods. _J. Phys. Chem. A_ 113, 4445–4450 (2009). Article  CAS 

PubMed  Google Scholar  * Baishya, K. et al. Optical absorption spectra of intermediate-size silver clusters from first principles. _Phys. Rev. B_ 78, 075439 (2008). Article  ADS  Google

Scholar  * Grigoryan, V., Springborg, M., Minassian, H. & Melikyan, A. Optical properties of silver and copper clusters with up to 150 atoms. _Comput. Theor. Chem._ 1021, 197–205 (2013).

Article  CAS  Google Scholar  * Hövel, H., Fritz, S., Hilger, A., Kreibig, U. & Vollmer, M. Width of cluster plasmon resonances: bulk dielectric functions and chemical interface

damping. _Phys. Rev. B_ 48, 18178 (1993). Article  ADS  Google Scholar  * Noguez, C. Surface plasmons on metal nanoparticles: the influence of shape and physical environment. _J. Phys. Chem.

C._ 111, 3806–3819 (2007). Article  CAS  Google Scholar  * Loginov, E. et al. Photoabsorption of Ag_n_ (n ~ 6–6000) nanoclusters formed in helium droplets: transition from compact to

multicenter aggregation. _Phys. Rev. Lett._ 106, 233401 (2011). * López Lozano, X., Mottet, C. & Weissker, H.-C. H. Effect of alloying on the optical properties of Ag-Au nanoparticles.

_J. Phys. Chem. C_ 117, 3062–3068 (2013). Article  Google Scholar  * Rossi, T. P., Kuisma, M., Puska, M. J., Nieminen, R. M. & Erhart, P. Kohn-Sham decomposition in real-time

time-dependent density-functional theory: An efficient tool for analyzing plasmonic excitations. _J. Chem. Theory Comput._ 13, 4779–4790 (2017). Article  CAS  PubMed  Google Scholar  *

Baseggio, O. et al. Photoabsorption of icosahedral noble metal clusters: An efficient TDDFT approach to large-scale systems. _J. Phys. Chem. C_ 120, 12773–12782 (2016). Article  CAS  Google

Scholar  * Fedrigo, S., Harbich, W. & Buttet, J. Collective dipole oscillations in small silver clusters embedded in rare-gas matrices. _Phys. Rev. B_ 47, 10706 (1993). Article  ADS  CAS

  Google Scholar  * Tiggesbäumker, J., Köller, L., Meiwes-Broer, K.-H. & Liebsch, A. Blue shift of the Mie plasma frequency in Ag clusters and particles. _Phys. Rev. A_ 48, R1749 (1993).

Article  ADS  PubMed  Google Scholar  * Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set.

_Comput. Mater. Sci._ 6, 15–50 (1996). Article  CAS  Google Scholar  * Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. _Phys. Rev. B_ 59,

1758 (1999). Article  ADS  CAS  Google Scholar  * Perdew, J. P. et al. Atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and

correlation. _Phys. Rev. B_ 46, 6671–6687 (1992). Article  ADS  CAS  Google Scholar  * Tancogne-Dejean, N. et al. Octopus, a computational framework for exploring light-driven phenomena and

quantum dynamics in extended and finite systems. _J. Chem. Phys._ 152, 124119 (2020). Article  ADS  CAS  PubMed  Google Scholar  * Troullier, N. & Martins, J. L. Efficient

pseudopotentials for plane-wave calculations. _Phys. Rev. B_ 43, 1993 (1991). Article  ADS  CAS  Google Scholar  * Harb, M. et al. Optical absorption of small silver clusters: Ag_n_, (n =

4–22). _J. Chem. Phys._ 129 (2008). * Iwe, N. et al. Metal cluster plasmons analyzed by energy-resolved photoemission. _Phys. Chem. Chem. Phys._ 25, 1677–1684 (2023). Article  CAS  PubMed 

Google Scholar  Download references ACKNOWLEDGEMENTS The authors thank Franck Rabillould for providing the geometries of the smaller clusters, which enabled the detailed comparisons in the

present work. Furthermore, the authors thank Jean Lermé, Matthias Hillenkamp, Gérard, Franck Rabilloud, and Lucia Reining for enlightening discussions. We acknowledge support from the French

National Research Agency (Agence Nationale de Recherche, ANR) in the frame of the project “SchNAPSS,” ANR-21-CE09-0021. The work has used HPC resources from GENCI-IDRIS (Grant

2022-0906829). Moreover, the authors acknowledge the contribution of the International Research Network IRN Nanoalloys (CNRS). Mohit C. thanks ED352 of Aix-Marseille University for the PhD

scholarship. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Aix-Marseille University, CNRS, CINaM UMR 7325, 13288, Marseille, France Mohit Chaudhary & Hans-Christian Weissker * European

Theoretical Spectroscopy Facility https://www.etsf.eu Mohit Chaudhary & Hans-Christian Weissker Authors * Mohit Chaudhary View author publications You can also search for this author

inPubMed Google Scholar * Hans-Christian Weissker View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS H.-C.W. conceived the project, M.C.

carried out the calculations. Both H.-C.W. and M.C. analyzed the data, worked out the comparison with experiment, and prepared the article. H.-C.W. supervised the project. CORRESPONDING

AUTHORS Correspondence to Mohit Chaudhary or Hans-Christian Weissker. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. PEER REVIEW PEER REVIEW INFORMATION

_Nature Communications_ thanks Jayedran C. Rasaiah and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available. ADDITIONAL

INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY

INFORMATION REPORTING SUMMARY PEER REVIEW FILE SOURCE DATA SOURCE DATA RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons

Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give

appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission

under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons

licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by

statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit

http://creativecommons.org/licenses/by-nc-nd/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Chaudhary, M., Weissker, HC. Optical spectra of silver clusters and

nanoparticles from 4 to 923 atoms from the TDDFT+_U_ method. _Nat Commun_ 15, 9225 (2024). https://doi.org/10.1038/s41467-024-53428-6 Download citation * Received: 14 December 2023 *

Accepted: 07 October 2024 * Published: 25 October 2024 * DOI: https://doi.org/10.1038/s41467-024-53428-6 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this

content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative