Dynamic gain and frequency comb formation in exceptional-point lasers

ABSTRACT Exceptional points (EPs)—singularities in the parameter space of non-Hermitian systems where two nearby eigenmodes coalesce—feature unique properties with applications such as

sensitivity enhancement and chiral emission. Existing realizations of EP lasers operate with static populations in the gain medium. By analyzing the full-wave Maxwell–Bloch equations, here

we show that in a laser operating sufficiently close to an EP, the nonlinear gain will spontaneously induce a multi-spectral multi-modal instability above a pump threshold, which initiates

an oscillating population inversion and generates a frequency comb. The efficiency of comb generation is enhanced by both the spectral degeneracy and the spatial coalescence of modes near an

EP. Such an “EP comb” has a widely tunable repetition rate, self-starts without external modulators or a continuous-wave pump, and can be realized with an ultra-compact footprint. We

develop an exact solution of the Maxwell–Bloch equations with an oscillating inversion, describing all spatiotemporal properties of the EP comb as a limit cycle. We numerically illustrate

this phenomenon in a 5-μm-long gain-loss coupled AlGaAs cavity and adjust the EP comb repetition rate from 20 to 27 GHz. This work provides a rigorous spatiotemporal description of the rich

laser behaviors that arise from the interplay between the non-Hermiticity, nonlinearity, and dynamics of a gain medium. SIMILAR CONTENT BEING VIEWED BY OTHERS TRACKING EXCEPTIONAL POINTS

ABOVE THE LASING THRESHOLD Article Open access 14 December 2023 FLOQUET TOPOLOGICAL DISSIPATIVE KERR SOLITONS AND INCOMMENSURATE FREQUENCY COMBS Article Open access 07 November 2024

NONLINEAR DYNAMICS AND KERR FREQUENCY COMB FORMATION IN LATTICES OF COUPLED MICRORESONATORS Article Open access 02 November 2023 INTRODUCTION An exceptional point (EP) is a non-Hermitian

degeneracy where not only do two eigenvalues coincide, but the spatial profiles of the two modes also become identical1,2,3,4,5. Realizing such non-Hermitian phenomena at steady-state

necessitates gain and loss, making microcavity lasers a fertile ground to explore EPs. The mode coalescence and corresponding topology of the eigenvalue landscape bestow EP lasers with

unique properties such as reversed pump dependence6, loss-induced lasing7, single-mode operation8,9, chiral emission10,11,12, sensitivity enhancement13,14,15,16,17,18, spectral phase

transitions19, and topological state transfer20. In semiconductor microcavity lasers, the frequency separation between lasing modes is typically large enough that the cross beats between

modes oscillate so fast that they average away before the gain medium can respond, leading to a static population inversion in the gain medium21. Previous realizations of EP lasers operated

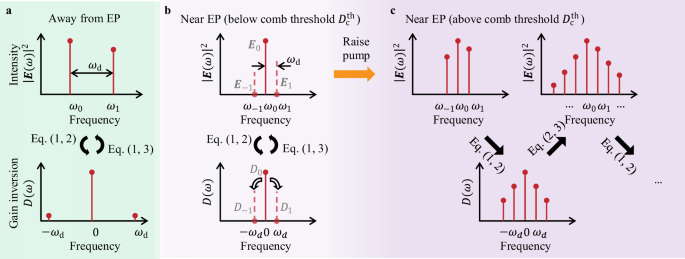
in this regime, yielding stable single-mode or few-mode behavior (Fig. 1a); these static-inversion lasers can be modeled by the “steady-state ab initio laser theory” (SALT)22,23,24,25,26. To

enhance the performance of EP-related phenomena, such as the sensitivity of EP sensors13,14,15,16,17,18, it is desirable to operate as close to an EP as possible. However, sufficiently

close to an EP, the vanishingly small eigenvalue difference (namely, frequency difference) means that any two lasing modes of a multimode system necessarily produce beat notes slow enough to

render the population inversion nonstationary. In general, since the population inversion determines the laser’s gain, any nonstationary inversion produced by beat notes acts as a periodic

modulation over the effective complex refractive index of the laser system. If gain’s periodic modulation frequency matches the cavity’s free spectral range (FSR) such that its high-quality

resonances can be excited, a frequency comb will form whose line spacing relies on the optical size of the cavities, examples of which include mode-locked laser combs27, Kerr combs28,29,

electro-optic combs30, and quantum cascade laser combs31,32,33. Thus, a laser operating close to an EP has two competing frequency scales, one set by the eigenvalue splitting, and the other

set by the cavity FSR; the former suggests that the system should become a comb due to population inversion dynamics, while the latter suggests that comb lines forming away from the cavity

resonances will experience too much radiative loss to persist. Unfortunately, existing theories34,35,36,37,38,39,40,41,42,43,44 cannot describe both the spatial complexity and the temporal

dynamics of the laser in this nonstationary-inversion regime. In this work, we develop a rigorous analysis of the full-wave Maxwell–Bloch equations and show that sufficiently close to an EP,

a laser necessarily develops into a frequency comb when pumped above a comb threshold \({D}_{{{\rm{c}}}}^{{{\rm{th}}}}\). In this operating regime, the nonlinear gain induces a

multi-spectral multi-modal perturbation that destabilizes single-mode operation and initiates temporal oscillations in the population inversion (Fig. 1b). The dynamic inversion then

nonlinearly couples different frequencies to produce a frequency comb above \({D}_{{{\rm{c}}}}^{{{\rm{th}}}}\) (Fig. 1c). As such, our framework demonstrates that a comb must form even

though the frequency of modulation driven by the dynamic inversion is typically orders of magnitude smaller than the FSR of the laser cavity. Distinct from conventional combs, such an “EP

comb” has a repetition rate independent of FSR, which enables a widely tunable repetition rate and a compact cavity size. The EP comb oscillation self-starts, forming spontaneously above a

pump threshold without an external modulator or an external continuous-wave laser. Moreover, we find the efficiency of comb teeth generation, characterized by a _ζ_ factor that we introduce,

to be enhanced by the spectral degeneracy and the spatial coalescence of the mode profile, conditions that are simultaneously met by operating near an EP. Finally, as an example, we provide

full-wave solutions of an EP comb in an AlGaAs gain-loss coupled cavity that is merely 5-μm long, demonstrating a continuously tunable repetition rate from 20 to 27 GHz, about 400 times

smaller than the free spectral range of this small cavity. Overall, the EP comb phenomena we predict provide a rich and unexpected intersection between non-Hermitian photonics, laser

physics, nonlinear dynamics, and frequency combs. RESULTS DYNAMIC INVERSION AND COMB FORMATION NEAR AN EXCEPTIONAL POINT To rigorously describe the wave physics and the spatiotemporal

complexity of an EP laser, we adopt the Maxwell–Bloch (MB) equations45,46 $$\frac{\partial }{\partial t}D=-{\gamma }_{\parallel }(D-{D}_{{{\rm{p}}}})-\frac{i{\gamma }_{\parallel

}}{2}({{{\bf{E}}}}^{*}\cdot {{\bf{P}}}-{{\bf{E}}}\cdot {{{\bf{P}}}}^{*}),$$ (1) $$\frac{\partial }{\partial t}{{\bf{P}}}=-(i{\omega }_{ba}+{\gamma }_{\perp }){{\bf{P}}}-i{\gamma }_{\perp

}D({{\bf{E}}}\cdot {{\mathbf{\theta }}}){{{\mathbf{\theta }}}}^{*},$$ (2) $$-\nabla \times \nabla \times {{\bf{E}}}-\frac{1}{{c}^{2}}\left({\varepsilon }_{c}\frac{{\partial }^{2}}{\partial

{t}^{2}}+\frac{\sigma }{{\varepsilon }_{0}}\frac{\partial }{\partial t}\right){{\bf{E}}}=\frac{1}{{c}^{2}}\frac{{\partial }^{2}}{\partial {t}^{2}}{{\bf{P}}}.$$ (3) The electrical field E(R, 

_t_) is described classically with Maxwell’s equations. The gain medium is described quantum mechanically as an ensemble of two-level atoms, leading to a population inversion _D_(R, _t_) and

inducing a polarization density P(R, _t_) that couple nonlinearly with E(R, _t_) through dipole interactions (Supplementary Sec. 1). The _D_, E, and P here are dimensionless as they have

been normalized by _R_2/(_ε_0_ℏ__γ_⊥), \(2R/(\hslash \sqrt{{\gamma }_{\perp }{\gamma }_{\parallel }})\), and \(2R/({\varepsilon }_{0}\hslash \sqrt{{\gamma }_{\perp }{\gamma }_{\parallel

}})\), respectively, with _R_ being the amplitude of the atomic dipole moment, _ε_0 the vacuum permittivity, _ℏ_ the Planck constant, and _γ_⊥ the dephasing rate of the gain-induced

polarization (i.e., the bandwidth of the gain). Here, _D_p(R) is the normalized net pumping strength and profile, _ω__b__a_ is the frequency gap between the two atomic levels, Θ is the unit

vector of the atomic dipole moment with Θ ⋅ Θ* = 1, _ε__c_(R) is the relative permittivity profile of the cold cavity, _σ_(R) is a conductivity profile that produces linear absorption, and

_c_ is the vacuum speed of light. E and P satisfy an outgoing boundary condition outside the cavity. When the pumping strength reaches the first lasing threshold \({D}_{1}^{{{\rm{th}}}}\),

the gain overcomes the radiation loss and absorption loss, and a single-mode lasing state \({{\bf{E}}}({{\bf{r}}},t)={{{\bf{E}}}}_{0}({{\bf{r}}}){e}^{-i{\omega }_{0}t}\) emerges at a

real-valued frequency _ω_0. Substituting this single-mode solution into the MB equations (Supplementary Sec. 2), we get $$\hat{O}\left({\omega }_{0}\right){{{\bf{E}}}}_{0}({{\bf{r}}})\equiv

\left[-\nabla \times \nabla \times+\frac{{\omega }_{0}^{2}}{{c}^{2}}{\varepsilon }_{{{\rm{eff}}}}({{\bf{r}}},{\omega }_{0})\right]{{{\bf{E}}}}_{0}({{\bf{r}}})=0.$$ (4) Here, _ε_eff(R, _ω_) =

 _ε__c_(R) + _i__σ_(R)/(_ω__ε_0) + _Γ_(_ω_)_D_0(R)Θ*Θ ⋅ is an effective intensity-dependent and frequency-dependent permittivity profile of the active cavity, and _Γ_(_ω_) ≡ _γ_⊥/(_ω_ − 

_ω__b__a_ + _i__γ_⊥). The gain _D_(R, _t_) = _D_0(R) = _D_p(R)/[1 + ∣_Γ_(_ω_0)E0(R) ⋅ Θ∣2] is nonlinearly saturated by the local intensity, referred to as spatial hole burning. In this

single-mode regime, Eq. (4) is an exact solution of the MB equations, the gain is static, and its relaxation rate _γ_∥ plays no role at steady state. One may freeze the nonlinearity by

considering a linear operator \(\hat{O}\left(\omega \right)\) in Eq. (4) that uses a fixed saturated gain _D_0(R) = _D_p(R)/[1 + ∣_Γ_(_ω_0)E0(R) ⋅ Θ∣2] for a fixed lasing intensity profile

∣E0(R)∣2. This linear \(\hat{O}\left(\omega \right)\) then admits eigenmodes \({\{{{{\boldsymbol{\psi }}}}_{n}({{\bf{r}}})\}}_{n}\) with complex-valued eigen frequencies \({\{{\tilde{\omega

}}_{n}\}}_{n}\), satisfying \(\hat{O}({\tilde{\omega }}_{n}){{{\boldsymbol{\psi }}}}_{n}=0\) with an outgoing boundary condition. We refer to them as the active-cavity resonances (also

called quasinormal modes47). We also define operator \(\hat{O}\left(\omega \right)\) below the first lasing threshold \({D}_{1}^{{{\rm{th}}}}\) simply using the linear unsaturated gain

_D_0(R) = _D_p(R). When we increase the pumping strength to \({D}_{1}^{{{\rm{th}}}}\), the eigenvalue \({\tilde{\omega }}_{0}={\omega }_{0}\) reaches the real-frequency axis, and that

resonance becomes the first lasing mode E0(R) ∝ _Ψ_0(R). In the following, we define an EP as where two eigenvalues \(\{{\tilde{\omega }}_{0},{\tilde{\omega }}_{1}\}\) of the linear operator

\(\hat{O}\left(\omega \right)\) coalesce, at which point the corresponding mode profiles {_Ψ_0, _Ψ_1} must also become the same given the non-Hermitian nature of \(\hat{O}\left(\omega

\right)\). An EP may exist at pumping strengths below the first lasing threshold \({D}_{1}^{{{\rm{th}}}}\); such a below-threshold EP can indirectly affect laser properties6,7,48 but cannot

be directly accessed since it does not correspond to a steady-state solution. In this paper, we consider a laser close to an accessible EP at pumping strengths near or above

\({D}_{1}^{{{\rm{th}}}}\). The SALT formalism assumes the population inversion to be static, _D_(R, _t_) = _D_0(R)22,23,24,25. Under SALT, the resonances {_Ψ__n_} are the modes that turn on

and lase when they receive enough gain. For a second mode _Ψ_1 to turn on, it must have a spatial profile sufficiently different from the lasing mode E0 ∝ _Ψ_0 that it can amplify using the

gain outside the spatial holes (i.e., away from the peaks of ∣_Ψ_0(R)∣2). Near an EP, _Ψ_1 necessarily has a similar spatial profile as _Ψ_0 and so cannot turn on. Therefore, SALT predicts

an EP laser to stay single-mode. However, this single-mode prediction is based on the static-inversion assumption, which is questionable near an EP since the slow beating between the two

very close-by frequencies may induce dynamics in the inversion _D_(R, _t_). To find out what actually happens to a laser close to an EP, one must go beyond SALT and account for the inversion

dynamics and its effects. To do so, we start with a monochromatic perturbation \({{{\bf{E}}}}_{1}({{\bf{r}}}){e}^{-i{\omega }_{1}t}\) (dashed line in Fig. 1b) to single-mode operation, so

the total field is \({{\bf{E}}}({{\bf{r}}},\,t)={{{\bf{E}}}}_{0}({{\bf{r}}}){e}^{-i{\omega }_{0}t}+{{{\bf{E}}}}_{1}({{\bf{r}}}){e}^{-i{\omega }_{1}t}\). The frequency difference _ω_d = _ω_1 

− _ω_0 can be positive or negative. With the inversion almost static, it follows from Eq. (2) that \({{\bf{P}}}({{\bf{r}}},\,t)={{{\bf{P}}}}_{0}({{\bf{r}}}){e}^{-i{\omega

}_{0}t}+{{{\bf{P}}}}_{1}({{\bf{r}}}){e}^{-i{\omega }_{1}t}\) with P_m_ = _Γ__m__D_0_E__m_Θ* for _m_ = 0, 1, where _Γ__m_ = _Γ_(_ω__m_) and _E__m_ ≡ E_m_ ⋅ Θ. We then see from Eq. (1) that

the inversion is no longer purely stationary; as illustrated in Fig. 1b, we now have \(D({{\bf{r}}},\,t)={D}_{-1}({{\bf{r}}}){e}^{i{\omega

}_{{{\rm{d}}}}t}+{D}_{0}({{\bf{r}}})+{D}_{1}({{\bf{r}}}){e}^{-i{\omega }_{{{\rm{d}}}}t}\) with a dynamic component induced by the perturbation,

$${D}_{-1}({{\bf{r}}})={D}_{1}^{*}({{\bf{r}}})=\frac{({\Gamma }_{0}-{\Gamma }_{1}^{*}){\gamma }_{\parallel }}{2(i{\gamma }_{\parallel }-{\omega

}_{{{\rm{d}}}})}{E}_{0}({{\bf{r}}}){E}_{1}^{*}({{\bf{r}}}){D}_{0}({{\bf{r}}}).$$ (5) This oscillating gain \({D}_{\pm 1}({{\bf{r}}}){e}^{\mp i{\omega }_{{{\rm{d}}}}t}\) arises from cross

beating in the nonlinear term E* ⋅ P of Eq. (1), so it is enhanced where _E_0(R) and _E_1(R) spatially overlap. Substituting _D_(R, _t_) into Eq. (2) yields a polarization P−1  = 

_Γ_−1(_D_−1_E_0 + _D_0_E_−1)Θ* at new frequency _ω_−1 = _ω_0 − _ω_d, which acts like a current source to produce a new field E−1 via Eq. (3), $$\left[-\nabla \times \nabla

\times+\frac{{\omega }_{-1}^{2}}{{c}^{2}}{\varepsilon }_{{{\rm{eff}}}}({{\bf{r}}},\,{\omega }_{-1})\right]{{{\bf{E}}}}_{-1}=-\frac{{\omega }_{-1}^{2}}{{c}^{2}}{\Gamma

}_{-1}{D}_{-1}{E}_{0}{{{\mathbf{\theta }}}}^{*}.$$ (6) This additional frequency component \({{{\bf{E}}}}_{-1}({{\bf{r}}}){e}^{-i{\omega }_{-1}t}\), generated in a four-wave-mixing49 fashion

by the nonlinear gain (Fig. 1b), differentiates an EP laser from a conventional laser and marks the onset of dynamic inversion and comb formation. To quantify the strength of this frequency

generation, we solve Eq. (6) to obtain (Supplementary Sec. 3) $$\frac{\langle |{{{\mathbf{E}}}}_{-1}|^2 \rangle}{\langle |{{{\mathbf{E}}}}_{1}|^2 \rangle} \approx

\underbrace{\frac{\gamma_\parallel^2}{\omega_{{{\rm{d}}}}^2+\gamma_\parallel^2} \frac{\omega_{0}^2}{4\omega_{{{\rm{d}}}}^2}}_{{{{\rm{I}}}}} \underbrace{\frac{\langle |{{{\mathbf{E}}}}_0|^2

\rangle \, |\langle D_0 E_{0}^3E_{1}^*\rangle|^2}{\langle |{{{\mathbf{E}}}}_{1}|^2\rangle \, |\langle \varepsilon_c {{{\mathbf{E}}}}_0\cdot{{{\mathbf{E}}}}_0\rangle|^2}}_{{{{\rm{II}}}}}

\equiv \zeta,$$ (7) which we denote as the dynamic inversion factor _ζ_. Here, 〈 ⋯  〉 = ∫( ⋯  )_d__r_3 denotes integration over space. We see _ζ_ is proportional to the lasing intensity

squared, ∣E0∣4, but independent of the perturbation strength ∣E1∣, so _ζ_ ≠ 0 even for an infinitesimal perturbation. The dynamic inversion factor _ζ_ has two ingredients, Factor I on the

spectral dependence, and Factor II on the spatial dependence and ∣E0∣4 laser intensity dependence. When the perturbation \({{{\bf{E}}}}_{1}{e}^{-i{\omega }_{1}t}\) overlaps well with the

long-lived resonances \(\{{{{\boldsymbol{\psi }}}}_{n}{e}^{-i{\tilde{\omega }}_{n}t}\}\), the response can sustain longer. So, the frequency difference _ω_d = _ω_1 − _ω_0 here correlates

with the eigenvalue difference \({\tilde{\omega }}_{1}-{\tilde{\omega }}_{0}\), which is minimized near an EP, enhancing Factor I through its \({\omega }_{{{\rm{d}}}}^{-4}\) scaling. The

resonances are biorthogonal with 〈_ε__c__ψ_0 ⋅ _ψ_1〉 ≈ 0. As the two resonances coalesce near an EP, E0 ∝ _ψ_0 ≈ _ψ_1, so 〈_ε__c_E0 ⋅ E0〉 ≈ 0, which enhances Factor II of _ζ_ in the same way

as how an EP enhances the Petermann factor _K_ ≡ ∣〈_ε__c_∣E0∣2〉/〈_ε__c_E0 ⋅ E0〉∣250,51,52,53,54,55,56,57. Such a mode coalescence promotes coupling through the stronger field overlap. In

Supplementary Sec. 4, we perform a stability analysis58,59 to determine the decay (or growth) rate of the multi-frequency perturbation \({{{\bf{E}}}}_{1}({{\bf{r}}}){e}^{-i{\omega

}_{1}t}+{{{\bf{E}}}}_{-1}({{\bf{r}}}){e}^{-i{\omega }_{-1}t}\). As the pumping strength increases, the decay rate crosses over to become a growth rate, and the crossover marks the next

threshold \({D}_{2}^{{{\rm{th}}}}\). This is where the infinitesimal multi-frequency perturbation materializes into sustained oscillations at _ω_±1. As the pump increases further, the new

frequencies induce higher harmonic oscillations in the population inversion, which generates more lasing frequencies. The process cascades down to produce a frequency comb (Fig. 1c).

Therefore, near an EP where the _ζ_ factor is substantial, \({D}_{2}^{{{\rm{th}}}}={D}_{{{\rm{c}}}}^{{{\rm{th}}}}\) is also the threshold where the frequency comb (indicated by the subscript

c) emerges, corresponding to a supercritical Hopf bifurcation60. We note that while the _ζ_ factor is resonantly enhanced, the beat frequency _ω_d and the coupled perturbation E±1(R) are

determined by the linear stability eigenproblem (Supplementary Sec. 4), not by Eq. (4) as in SALT. Therefore, E±1(R) is generally _not_ an active-cavity resonance _Ψ__n_ but a superposition

of multiple resonances, and the comb spacing _ω_d is correlated with but not identical to the resonance spacing \(| {\tilde{\omega }}_{1}-{\tilde{\omega }}_{0}|\). EXACT DYNAMIC SOLUTION:

PALT The preceding analysis predicts comb formation near an EP and its threshold. To additionally predict the laser behavior above \({D}_{{{\rm{c}}}}^{{{\rm{th}}}}\) such as the the

evolution of the comb-line intensities, repetition rate, spatial profiles, and temporal dynamics, one must address the coupling between all frequency components self-consistently. Since the

cascade process couples frequencies separated by _ω_d = _ω_1 − _ω_0, we postulate the following spatiotemporal dependence at large time61,62 $${{\bf{E}}}({{\bf{r}}},\,t)={e}^{-i{\omega

}_{0}t}\sum_{m=-\infty }^{+\infty }{{{\bf{E}}}}_{m}({{\bf{r}}}){e}^{-im{\omega }_{{{\rm{d}}}}t},$$ (8) $${{\bf{P}}}({{\bf{r}}},\,t)={e}^{-i{\omega }_{0}t}\sum_{m=-\infty }^{+\infty

}{{{\mathbf{\theta }}}}^{*}{P}_{m}({{\bf{r}}}){e}^{-im{\omega }_{{{\rm{d}}}}t},$$ (9) $$D({{\bf{r}}},\,t)=\sum_{m=-\infty }^{+\infty }{D}_{m}({{\bf{r}}}){e}^{-im{\omega }_{{{\rm{d}}}}t},$$

(10) with _ω_0, _ω_d, and _D_(R, _t_) being real numbers. This ansatz describes a limit cycle60, which is periodic in time and therefore represented rigorously by a Fourier series. It also

describes single-mode and two-mode operation as special cases but excludes operating with more than two cavity modes or a chaotic dynamics. The temporal periodicity is _τ_ = 2_π_/_ω_d. We

show in Sec. METHODS that the ansatz of Eqs. (8–10) forms an exact solution of the full-wave MB equations, Eqs. (1–3), with no approximation. Eliminating the gain-induced polarization yields

a coupled nonlinear equation for {E_m_} $$-\nabla \times \nabla \times {{{\bf{E}}}}_{m}+\frac{{\omega }_{m}^{2}}{{c}^{2}}\left({\varepsilon }_{c}+\frac{i\sigma }{{\omega }_{m}{\varepsilon

}_{0}}\right){{{\bf{E}}}}_{m}=-\frac{{\omega }_{m}^{2}}{{c}^{2}}{\Gamma }_{m}\sum_{n=-\infty }^{+\infty }{D}_{m-n}({{{\bf{E}}}}_{n}\cdot {{\mathbf{\theta }}}){{{\mathbf{\theta }}}}^{*},$$

(11) and {_D__m_} $$\bar{D}={D}_{{{\rm{p}}}}{\left[\bar{\bar{I}}-0.5{\bar{\bar{\Gamma }}}_{\parallel }\left({\bar{\bar{E}}}^{{\dagger} }{\bar{\bar{\Gamma

}}}_{+}\bar{\bar{E}}-\bar{\bar{E}}{\bar{\bar{\Gamma }}}_{-}^{{\dagger} }{\bar{\bar{E}}}^{{\dagger} }\right)\right]}^{-1}\bar{\delta },$$ (12) with _ω__m_ = _ω_0 + _m__ω_d. Different

frequency components E_m_ are coherently coupled through a dynamic inversion _D__m_−_n_ oscillating at the frequency difference. Here, \(\bar{D}\) and \(\bar{\delta }\) are column vectors

with elements \({(\bar{D})}_{m}={D}_{m}\) and \({(\bar{\delta })}_{m}={\delta }_{m}\), where _δ__m_ is the Kronecker delta with _δ_0 = 1 and _δ__m_≠0 = 0; \(\bar{\bar{I}}\) is the identity

matrix; \(\bar{\bar{E}}\) is a full matrix with elements \({(\bar{\bar{E}})}_{mn}={{{\bf{E}}}}_{m-n}\cdot {{\mathbf{\theta }}}\); † denotes matrix conjugate transpose; \({\bar{\bar{\Gamma

}}}_{\parallel }\) and \({\bar{\bar{\Gamma }}}_{\pm }\) are diagonal matrices with \({({\bar{\bar{\Gamma }}}_{\parallel })}_{mn}={\delta }_{m-n}{\gamma }_{\parallel }/(m{\omega

}_{{{\rm{d}}}}+i{\gamma }_{\parallel })\) and \({({\bar{\bar{\Gamma }}}_{\pm })}_{mn}={\delta }_{m-n}{\Gamma }_{\pm m}\), where _Γ__m_ = _Γ_(_ω__m_) = _γ_⊥/(_ω__m_ − _ω__b__a_ + _i__γ_⊥) was

defined earlier. Solving Eqs. (11, 12) for {E_m_(R)}, {_D__m_(R)}, _ω_0, and _ω_d yields all properties of the laser comb, including the frequency spectrum, temporal dynamics, spatial

profiles, and input-output curves. To match the number of equations and the number of unknowns, we fix two gauge variables by recognizing that when E(R, _t_) is a solution, _e__i__ϕ_E(R, _t_

 − _t_0) with any real-valued _ϕ_ and _t_0 is also a solution. We name this formalism “periodic-inversion ab initio laser theory” (PALT), which overcomes the stationary-inversion limitation

of SALT. Note there is no sharp transition between an ordinary two-mode laser and an EP comb. An ordinary laser operating in the two-mode regime away from degeneracies is a trivial limit

cycle with two dominant frequency components and is also rigorously described by Eqs. (8–12). Such a laser features a small _ζ_ factor, so the second threshold \({D}_{2}^{{{\rm{th}}}}\) from

the stability analysis reduces to the SALT threshold (Supplementary Sec. 4), and the intensities of the additional frequency components (_m_ ≠ 0, 1) are small enough to be neglected. When

_ζ_ is raised, \({D}_{2}^{{{\rm{th}}}}\) smoothly moves, and the additional frequency components above \({D}_{2}^{{{\rm{th}}}}\) smoothly increase. Up to now, we have considered MB equations

with an ensemble of two-level atoms. In Supplementary Sec. 5, we generalize the MB equations to account for the band structure in semiconductor gain media and correspondingly generalize the

PALT formalism, which does not change the conclusion on comb formation near an EP. EP COMB EXAMPLE We now use explicit full-wave examples for illustration. We adopt a

parity-time-symmetric-like configuration3,4,63, where a gain cavity is coupled to a passive cavity with material loss (Fig. 2a). Supplementary Sec. 6 lists the system parameters. The

coupling and the gain-loss contrast are ingredients for an EP1,2,3,4,5. Distributed Bragg reflectors (DBRs) are used to enclose the two cavities and to separate them. The gain cavity

consists of AlGaAs (refractive index \(\sqrt{{\varepsilon }_{c}}=3.4\)64, gain center \({\tilde{\omega }}_{ba}=2\pi c/{\omega }_{ba}=820\) nm, gain width _γ_⊥ = 1013 s−1, and relaxation rate

_γ_∥ = 109 s−1)65. The PALT formalism applies to any pumping profile _D_p(R); to improve the accuracy of the slow finite-difference time-domain (FDTD) simulations that we perform for

validation, here we adopt a smooth profile \({D}_{{{\rm{p}}}}(x)=0.5{D}_{\max }[1-\cos (2\pi x/L)]\). The other cavity consists of passive GaAs (\(\sqrt{{\varepsilon }_{c}}=3.67\))64 with a

material absorption characterized by a conductivity _σ_. The system is homogeneous in the transverse directions (_y_ and _z_), so it reduces to a 1D problem with

\({{{\bf{E}}}}_{m}({{\bf{r}}})={E}_{m}(x)\hat{z}\). In Fig. 2b, c, we show the two eigen frequencies \(\{{\tilde{\omega }}_{0},{\tilde{\omega }}_{1}\}\) of the linear operator

\(\hat{O}\left(\omega \right)\) of Eq. (4) as a function of the pumping strength \({D}_{\max }\) and the length of the passive cavity, _L_2 = 1340 nm + Δ. To illustrate the presence of an

EP, in this figure (and this figure only) we adopt a linear gain _D_0(_x_) = _D_p(_x_) with no saturation, yielding two Riemann sheets that meet at an EP at \({D}_{\max

}=0.0126,\Delta=0.01\,\,{\mbox{nm}}\,\), \({\tilde{\omega }}_{0}={\tilde{\omega }}_{1}={\tilde{\omega }}_{{{\rm{EP}}}}=2\pi \times 365.43\,\,{\mbox{THz}}\,-i0.0356\,{{\mbox{ps}}}^{-1}\)

(green circle). Next, we fix the length of the passive cavity at _L_2 = 1340 nm (Δ = 0), for which the pump dependence of the two eigenvalues is shown by the red (_n_ = 0) and blue (_n_ = 1)

curves in Fig. 2b–d. At pumping strength \({D}_{\max }={D}_{1}^{{{\rm{th}}}}=0.0124\) (red and blue filled circles in Fig. 2d), \({\tilde{\omega }}_{0}\) reaches the real-frequency axis,

and _E_0(_x_) ∝ _ψ_0(_x_) turns on as the first lasing mode; the Petermann factor there is \({K}_{0}\equiv | \langle {\varepsilon }_{c}| {\psi }_{0}{| }^{2}\rangle /\langle {\varepsilon

}_{c}{\psi }_{0}^{2}\rangle {| }^{2}=28\). Above the first threshold (\({D}_{1}^{{{\rm{th}}}}\, < \,{D}_{\max } < {D}_{2}^{{{\rm{th}}}}\)), the red and blue dashed lines in Fig. 2b–d

show the would-be eigenvalue trajectories with a hypothetical linear gain, in which case the system enters a PT-broken phase where one mode is localized in the pumped cavity, and the other

mode is localized in the lossy cavity. Gain saturation, however, clamps the saturated gain at the same level as the overall loss, which fixes the two nonlinearity-frozen eigenvalues

\(\{{\tilde{\omega }}_{0},{\tilde{\omega }}_{1}\}\) near where they are at \({D}_{1}^{{{\rm{th}}}}\) (red and blue filled circles in Fig. 2d), and this single-mode laser stays close to a

nonlinear EP without entering the PT-broken phase. As the pumping strength reaches above \({D}_{\max }\, > \,{D}_{2}^{{{\rm{th}}}}={D}_{{{\rm{c}}}}^{{{\rm{th}}}}=0.064\), the population

inversion starts to oscillate (Fig. 3e), and a frequency comb emerges (Fig. 3g). Given the proximity to an EP, the repetition rate ∣_ω_d∣ ≈1.35 × 1011 rad/s at

\({D}_{{{\rm{c}}}}^{{{\rm{th}}}}\) is around 400 times smaller than the FSR of the overall cavity, and the dynamic inversion factor _ζ_ ≈0.26 is sizeable. For a complete characterization, we

show in Fig. 4a the evolution of the intensity at different frequencies as a function of the pumping strength. To keep the frequency difference ∣_ω_d∣ small, we raise the absorption level

_σ_ when \({D}_{\max }\, > \,{D}_{{{\rm{c}}}}^{{{\rm{th}}}}\) (Fig. 4b, c). The two center comb lines {_ω_0, _ω_1} lie close to the two near-degenerate active-cavity resonances from SALT

in Eq. (4), \(\{{{\rm{Re}}}({\tilde{\omega }}_{0}),\,{{\rm{Re}}}({\tilde{\omega }}_{1})\}\); the remaining comb lines are generated by the nonlinear gain through four-wave mixing and are not

lined up with any additional cavity modes (Supplementary Fig. 3). The spatial profiles at different frequencies are almost identical (Fig. 3c); they remain comparable to the profiles near

the EP in the single-mode regime \({D}_{1}^{{{\rm{th}}}}\, < \,{D}_{\max } < \, {D}_{2}^{{{\rm{th}}}}\) where the two modes almost coalesce, without entering the PT-broken phase.

Supplementary Sec. 6 shows the intensity and gain profiles at all frequencies and their relative phases. It is commonly assumed21,25,26,58,59 that the stationary-inversion approximation

(SIA) of SALT is valid when ∣_ω_d∣ > _γ_∥, namely when the beat notes oscillate faster than the gain relaxation rate. However, such a reasoning does not account for the EP-enhanced

frequency generation, as captured by the dynamic inversion factor _ζ_ in Eq. (7). In the present example, ∣_ω_d∣ ≈1.35 × 1011 rad/s is two orders of magnitude greater than _γ_∥ = 109 s−1,

but SALT (blue circle in Fig. 3g and red dashed line in Fig. 4a) already fails above the comb threshold. As described in Sec. Dynamic inversion and comb formation near an exceptional point

and shown in Fig. 2d, SALT predicts the laser to stay single-mode because _ψ_1(_x_) has almost the same spatial profile as the lasing mode _E_0(_x_) ∝ _ψ_0(_x_) near an EP, so it experiences

the same gain clamping as _E_0(_x_) and cannot turn on; this would indeed be the laser behavior when the system is near an EP but not close enough. In the present example, given the very

close proximity to an EP and the resulting large dynamic inversion factor _ζ_ ≈0.26, what actually turns on at the comb threshold \({D}_{2}^{{{\rm{th}}}}={D}_{{{\rm{c}}}}^{{{\rm{th}}}}\) is

not an isolated resonance _ψ_1 of the operator \(\hat{O}\left(\omega \right)\) in Eq. (4) but the multi-spectral multi-modal perturbation \({E}_{1}(x){e}^{-i{\omega

}_{1}t}+{E}_{-1}(x){e}^{-i{\omega }_{-1}t}\) described in Sec. Dynamic inversion and comb formation near an exceptional point, which is a superposition of multiple resonances and can amplify

by additionally utilizing the dynamic gain \({D}_{\pm 1}(x){e}^{\mp i{\omega }_{{{\rm{d}}}}t}\) of Eq. (5). As a comparison to the near-EP laser above, we also consider an ordinary

single-cavity laser (Fig. 3b) sandwiched between two DBR partial mirrors, operating in the two-mode regime. The active cavity has the same AlGaAs gain. At pumping strength \({D}_{\max }\,

> \,{D}_{2}^{{{\rm{th}}}}=0.033\), two modes that differ by one longitudinal order lase (Fig. 3d) and produce a sinusoidal beating pattern (Fig. 3f). Here, the population inversion is

static (Fig. 3f), and only two peaks appear in the spectrum (Fig. 3h). There is no EP nearby in the parameter space. The frequency separation \(| {\omega }_{{{\rm{d}}}}| \approx \pi

c/\sqrt{{\varepsilon }_{c}}L\approx 5.4\times 1{0}^{13}\) rad/s equals the free spectral range (FSR) of the cavity and is over four orders of magnitude greater than _γ_∥, leading to a

negligible dynamic inversion factor _ζ_ ≈ 3 × 10−13. The Petermann factor is _K_ = 1.0 here; the gain only balances the radiation loss and does not introduce mode non-orthogonality. For such

a two-mode laser away from degeneracies, PALT reduces to SALT (blue circles in Fig. 3h). EPs feature a boosted sensitivity13,14,15,16,17,18, which also amplifies the numerical error,

requiring an unusually high precision when solving Eqs. (11–12). We find a finite-difference discretization25 and the threshold constant-flux basis24 to both require an impractically large

basis to reach a satisfactory accuracy near an EP. To improve the numerical efficiency, here we develop a volume-integral formalism that employs accurate semi-analytic Green’s function of

the passive system to solve Eqs. (11, 12) (Supplementary Sec. 7). To validate our prediction and to verify the stability of the single-mode and the comb solutions, we additionally carry out

direct integration of the MB equations, Eqs. (1–3), using FDTD, where we evolve the system until all transient behaviors settle away (Supplementary Sec. 8). The time-consuming FDTD

simulations agree quantitatively with all of the PALT predictions (Figs. 3–4). Figure 4d shows the field evolution in FDTD when the pump is raised across the comb threshold. Since the EP

comb repetition rate _f_d = ∣_ω_d∣/(2_π_) is not tied to the cavity FSR, we can adjust it freely, for example, by tuning the material absorption as shown in Fig. 5. This is not possible with

mode-locked combs, Kerr combs, and quantum cascade laser combs. In the preceding example, we bring the laser close to an EP. Supplementary Sec. 9 shows that the behavior is the same when we

tune the system parameters with a higher precision such that the system has an almost exact EP above the first threshold, \({D}_{{{\rm{EP}}}} > {D}_{1}^{{{\rm{th}}}}\). With increasing

pump (while fixing the other system parameters), such a laser reaches the comb threshold \({D}_{{{\rm{c}}}}^{{{\rm{th}}}}\) and develops into a stable EP comb soon after

\({D}_{1}^{{{\rm{th}}}}\). The exact-EP single-mode lasing state is unreachable as it lies at a higher pump (namely, \({D}_{{{\rm{EP}}}}\, > \,{D}_{{{\rm{c}}}}^{{{\rm{th}}}}\gtrsim

{D}_{1}^{{{\rm{th}}}}\)) and is unstable. DISCUSSION In this work, we answer the question of what happens to a laser close to an EP. Based on the full-wave MB equations, we show that the

spectral degeneracy and the spatial coalescence of modes near an EP work with the nonlinearity of the gain medium to induce oscillations in the population inversion, resulting in an “EP

comb.” The EP comb features a continuously tunable repetition rate, an ultra-compact cavity size, and a self-starting operation with no need for an external modulator or continuous-wave

laser. The PALT formalism fully describes both the spatial complexity and the temporal dynamics of such a limit-cycle laser state, overcoming the stationary-inversion limitation of SALT.

This EP comb phenomenon uniquely bridges the subjects of non-Hermitian photonics, laser physics, nonlinear dynamics, and frequency combs. As EP sensors are more sensitive closer to an

EP13,14,15,16,17,18, it may be desirable to operate such a sensor as close to an EP as possible. This work shows that when an EP laser is brought sufficiently close to an EP, it necessarily

develops into a comb above a pump threshold. In such a comb regime, the optimal sensing scheme and the parametric dependence are nontrivial and can be the subject of a future study. Existing

realizations of EP lasers had mode spacing above 100 GHz; given the \({\omega }_{{{\rm{d}}}}^{-4}\) scaling of the dynamic inversion factor _ζ_ in Eq. (7), the _ζ_’s there were too small to

induce the multi-spectral multi-modal instability responsible for comb formation, so those lasers exhibited static single-mode behavior. Further reduction of the mode spacing requires finer

tuning but is possible. In fact, the self-pulsation observed in an InAs-quantum-dot Fano laser66 may have been an EP comb since that system has the features of an EP comb (self-starting

comb formation in a compact microcavity) and all the EP ingredients: two modes with similar frequencies (one from a line-defect waveguide and one from a nanocavity), near-field coupling

between the two modes, and differential gain (as only the waveguide is pumped). The repetition rate ∣_ω_d∣ of the EP comb is determined by the stability eigenvalue problem (Supplementary

Sec. 4) at the threshold \({D}_{{{\rm{c}}}}^{{{\rm{th}}}}\) and by solving the nonlinear Eqs. (11, 12) self-consistently above \({D}_{{{\rm{c}}}}^{{{\rm{th}}}}\). While it is hard to extract

insights from these complex equations, empirically we found the distance between the two linear SALT eigenvalues of Eq. (4) to provide a crude approximation, \(| {\omega }_{{{\rm{d}}}}|

\approx | {\tilde{\omega }}_{1}-{\tilde{\omega }}_{0}|\), near \({D}_{{{\rm{c}}}}^{{{\rm{th}}}}\). Close to an EP, the two linear eigenvalues are sensitive to all parameters of the system,

so _ω_d can be tuned by changing the absorption, coupling strength, refractive index, etc. The repetition rate can also be reduced by considering larger cavities. The minimal repetition rate

is limited by the laser linewidth, which can be reduced with standard methods. The limit of the linewidth itself would be an interesting subject for future investigations. The divergent

Petermann factor is known to broaden the linewidth50,51,56,57,67. With an EP comb, we expect even richer noise properties since the dynamic population inversion can modify the spontaneous

emission beyond noise models that assume a linear gain54,68 or a stationary inversion42,51,57,69,70. Additionally, the relation between noise and atomic populations is commonly derived at a

local thermal equilibrium51,69, but such an equilibrium is no longer reached when the inversion fluctuates faster than the spontaneous emission rate. An EP comb provides a doorway to other

nonlinear dynamics phenomena such as bistability, period doubling, and chaos. Future work can study the stability of the EP comb, its bifurcation properties, and the transition to other

dynamic regimes. The comb spectrum may be further analyzed and optimized. The PALT formalism can also describe lasers near Hermitian degeneracies due to symmetry, going beyond perturbation

theory26 and stability analysis58,59. We expect even richer behaviors near higher-order EPs and in spatially complex systems such as random lasers and chaotic-cavity lasers. METHODS

DERIVATION OF PALT We show that the PALT ansatz in Eqs. (8–10) forms an exact solution of the MB equations. In doing so, we also derive Eqs. (11, 12). We substitute Eqs. (8–10) into the MB

equations, Eqs. (1–3), and match terms with the same time dependence. Solving Eq. (1), we get $${D}_{m}={D}_{{{\rm{p}}}}{\delta }_{m}+\frac{1}{2}\frac{{\gamma }_{\parallel }}{m{\omega

}_{d}+i{\gamma }_{\parallel }}\sum_{n=-\infty }^{+\infty }\left({{{\bf{E}}}}_{-m+n}^{*}\cdot {{{\mathbf{\theta }}}}^{*}{P}_{n}-{{{\bf{E}}}}_{m-n}\cdot {{\mathbf{\theta

}}}{P}_{-n}^{*}\right),$$ (13) where _δ__m_ is the Kronecker delta with _δ_0 = 1 and _δ__m_≠0 = 0. From Eq. (2), we get $${P}_{m}={\Gamma }_{m}\sum_{n=-\infty }^{+\infty

}{D}_{n}{{{\bf{E}}}}_{m-n}\cdot {{\mathbf{\theta }}},$$ (14) where _Γ__m_ = _Γ_(_ω__m_) = _γ_⊥/(_ω__m_ − _ω__b__a_ + _i__γ_⊥) and _ω__m_ = _m__ω_d + _ω_0. From Eq. (3), we get $$-\nabla

\times \nabla \times {{{\bf{E}}}}_{m}+\frac{{\omega }_{m}^{2}}{{c}^{2}}\left({\varepsilon }_{c}+\frac{i\sigma }{{\omega }_{m}{\varepsilon }_{0}}\right){{{\bf{E}}}}_{m}=-\frac{{\omega

}_{m}^{2}}{{c}^{2}}{P}_{m}{\hat{{{\mathbf{\theta }}}}}^{*}.$$ (15) This confirms that all of the MB equations, Eqs. (1–3), are satisfied with no approximation. Substituting Eq. (14) into Eq.

(15), we get Eq. (11), where we have applied the commutativity of convolution, $$\sum_{n=-\infty }^{+\infty }{D}_{n}{{{\bf{E}}}}_{m-n}\cdot {{\mathbf{\theta }}}=\sum_{n=-\infty }^{+\infty

}{D}_{m-n}{{{\bf{E}}}}_{n}\cdot {{\mathbf{\theta }}}.$$ (16) To eliminate the gain-induced polarization, we first recognize that since _D_(R, _t_) is real-valued, its Fourier components have

to be symmetric, \({D}_{n}^{*}={D}_{-n}\). With this fact, we take the complex conjugate of Eq. (14) and then replace the dummy variable _n_ by  − _n_, $${P}_{-m}^{*}={\Gamma

}_{-m}^{*}\sum_{n=-\infty }^{+\infty }{D}_{n}^{*}{{{\bf{E}}}}_{-m-n}^{*}\cdot {{\mathbf{\theta }}}\\={\Gamma }_{-m}^{*}\sum_{n=-\infty }^{+\infty }{D}_{-n}{{{\bf{E}}}}_{-m-n}^{*}\cdot

{{\mathbf{\theta }}}\\={\Gamma }_{-m}^{*}\sum_{n=-\infty }^{+\infty }{D}_{n}{{{\bf{E}}}}_{-m+n}^{*}\cdot {{\mathbf{\theta }}}.$$ (17) Eqs. (13, 14, 17) can be summarized in matrix form as

$$\bar{D}={D}_{{{\rm{p}}}}\bar{\delta }+\frac{1}{2}{\bar{\bar{\Gamma }}}_{\parallel }({\bar{\bar{E}}}^{{\dagger} }\bar{P}-\bar{\bar{E}}{\bar{P}}_{-}^{*}),$$ (18) $$\bar{P}={\bar{\bar{\Gamma

}}}_{+}\bar{\bar{E}}\bar{D},$$ (19) $${\bar{P}}_{-}^{*}={\bar{\bar{\Gamma }}}_{-}^{{\dagger} }{\bar{\bar{E}}}^{{\dagger} }\bar{D},$$ (20) where † denotes matrix conjugate transpose, with *

Column vectors: \({(\bar{P})}_{m}={P}_{m}\), \({({\bar{P}}_{-}^{*})}_{m}={P}_{-m}^{*}\), \({(\bar{D})}_{m}={D}_{m}\), and \({(\bar{\delta })}_{m}={\delta }_{m}\). * Matrices:

\({(\bar{\bar{E}})}_{mn}={{{\bf{E}}}}_{m-n}\cdot \hat{{{\mathbf{\theta }}}}\), \({({\bar{\bar{\Gamma }}}_{\parallel })}_{mn}={\delta }_{m-n}{\gamma }_{\parallel }/(m{\omega

}_{{{\rm{d}}}}+i{\gamma }_{\parallel })\), \({({\bar{\bar{\Gamma }}}_{\pm })}_{mn}={\delta }_{m-n}{\Gamma }_{\pm m}\). Substituting Eqs. (19, 20) into Eq. (18), we can solve for \(\bar{D}\)

to obtain Eq. (12). SLOW-GAIN LIMIT In the slow-gain limit of ∣_ω__d_∣ ≫ _γ_∥, all entries of the diagonal matrix \({\bar{\bar{\Gamma }}}_{\parallel }\) are approximately 0 except

\({({\bar{\bar{\Gamma }}}_{\parallel })}_{00}=-i\). In this limit, Eq. (12) simplifies to \(\bar{D}\approx {D}_{0}\bar{\delta }\) with $${D}_{0}({{\bf{r}}})\approx

\frac{{D}_{{{\rm{p}}}}({{\bf{r}}})}{1+{\sum}_{m}| {\Gamma }_{m}{{{\bf{E}}}}_{m}({{\bf{r}}})\cdot {{\mathbf{\theta }}}{| }^{2}}.$$ (21) Then, Eq. (19) yields _P__m_ ≈ _Γ__m__D_0(E_m_ ⋅ Θ), so

Eq. (11) becomes $$\left[-\nabla \times \nabla \times+\frac{{\omega }_{m}^{2}}{{c}^{2}}\left({\varepsilon }_{c}+\frac{i\sigma }{{\omega }_{m}{\varepsilon }_{0}}+{\Gamma

}_{m}{D}_{0}{{{\mathbf{\theta }}}}^{*}{{\mathbf{\theta }}}\cdot \right)\right]{{{\bf{E}}}}_{m}\approx 0.$$ (22) These Eqs. (21, 22) reduce to SALT24,25 in the single-mode or two-mode regime

(with two indices, _m_ = 0, 1; E_m_ with _m_ ≠ 0 or 1 has to be zero unless _ω__m_ happens to be the resonant frequency of a third lasing mode). FAST-GAIN LIMIT In the fast-gain limit where

the lasing bandwidth is much smaller than both _γ_∥ and _γ_⊥, we can show that \({\bar{\bar{\Gamma }}}_{\parallel }\approx -i\bar{\bar{I}}\), \({\bar{\bar{\Gamma }}}_{\pm }\approx {\Gamma

}_{0}\bar{\bar{I}}\), and \({\bar{\bar{E}}}^{{\dagger} }\bar{\bar{E}}=\bar{\bar{E}}{\bar{\bar{E}}}^{{\dagger} }\). In this limit, Eq. (12) simplifies to $$\bar{D}\approx

{D}_{{{\rm{p}}}}{(\bar{\bar{I}}+| {\Gamma }_{0}{| }^{2}{\bar{\bar{E}}}^{{\dagger} }\bar{\bar{E}})}^{-1}\bar{\delta },$$ (23) where we have applied \({\Gamma }_{0}-{\Gamma }_{0}^{*}=-2i|

{\Gamma }_{0}{| }^{2}\). Eq. (23) yields $$\bar{D}+| {\Gamma }_{0}{| }^{2}{\bar{\bar{E}}}^{{\dagger} }\bar{\bar{E}}\bar{D}\approx {D}_{{{\rm{p}}}}\bar{\delta }.$$ (24) The entries of the

column vector \({\bar{\bar{E}}}^{{\dagger} }\bar{\bar{E}}\bar{D}\) are the Fourier components of \(| {{\bf{E}}}({{\bf{r}}},t)\cdot \hat{{{\mathbf{\theta }}}}{| }^{2}D({{\bf{r}}},t)\).

Therefore, if we multiply Eq. (24) to the left with the row vector \([...,\,{e}^{2i{\omega }_{{{\rm{d}}}}t},\,{e}^{i{\omega }_{{{\rm{d}}}}t},\,1,\,{e}^{-i{\omega

}_{{{\rm{d}}}}t},\,{e}^{-2i{\omega }_{{{\rm{d}}}}t},...]\), we obtain the time evolution \(D({{\bf{r}}},\,t)+| {\Gamma }_{0}{{\bf{E}}}({{\bf{r}}},\,t)\cdot \hat{{{\mathbf{\theta }}}}{|

}^{2}D({{\bf{r}}},\,t)\approx {D}_{{{\rm{p}}}}({{\bf{r}}})\), namely $$D({{\bf{r}}},\,t)\approx \frac{{D}_{{{\rm{p}}}}({{\bf{r}}})}{1+| {\Gamma }_{0}{{\bf{E}}}({{\bf{r}}},\,t)\cdot

\hat{{{\mathbf{\theta }}}}{| }^{2}}.$$ (25) In this fast-gain limit, the instantaneous population inversion is given by the instantaneous intensity at that time. DATA AVAILABILITY The data

of PALT calculation and FDTD simulation results presented in the paper are available on OSF database [https://osf.io/jptza/]. CODE AVAILABILITY Codes that reproduce the results in this

study, including the PALT integral equation solver, stability eigenvalue solver, and Maxwell–Bloch FDTD simulations, are available on GitHub [https://github.com/complexphoton/PALT].

REFERENCES * Moiseyev, N. _Non-Hermitian Quantum Mechanics_ (Cambridge Univ. Press, 2011). * Heiss, W. D. The physics of exceptional points. _J. Phys. A Math. Theor._ 45, 444016 (2012).

Article  ADS  MathSciNet  Google Scholar  * Feng, L., El-Ganainy, R. & Ge, L. Non-Hermitian photonics based on parity–time symmetry. _Nat. Photon._ 11, 752–762 (2017). Article  ADS  CAS

  Google Scholar  * El-Ganainy, R. et al. Non-Hermitian physics and PT symmetry. _Nat. Phys._ 14, 11–19 (2018). Article  CAS  Google Scholar  * Miri, M.-A. & Alù, A. Exceptional points

in optics and photonics. _Science_ 363, eaar7709 (2019). Article  MathSciNet  CAS  PubMed  Google Scholar  * Liertzer, M. et al. Pump-induced exceptional points in lasers. _Phys. Rev. Lett._

108, 173901 (2012). Article  ADS  CAS  PubMed  Google Scholar  * Peng, B. et al. Loss-induced suppression and revival of lasing. _Science_ 346, 328–332 (2014). Article  ADS  CAS  PubMed 

Google Scholar  * Feng, L., Wong, Z. J., Ma, R.-M., Wang, Y. & Zhang, X. Single-mode laser by parity-time symmetry breaking. _Science_ 346, 972–975 (2014). Article  ADS  CAS  PubMed 

Google Scholar  * Hodaei, H., Miri, M.-A., Heinrich, M., Christodoulides, D. N. & Khajavikhan, M. Parity-time-symmetric microring lasers. _Science_ 346, 975–978 (2014). Article  ADS  CAS

  PubMed  Google Scholar  * Peng, B. et al. Chiral modes and directional lasing at exceptional points. _Proc. Natl Acad. Sci. USA_ 113, 6845–6850 (2016). Article  ADS  CAS  PubMed  PubMed

Central  Google Scholar  * Miao, P. et al. Orbital angular momentum microlaser. _Science_ 353, 464–467 (2016). Article  ADS  CAS  PubMed  Google Scholar  * Zhang, Z. et al. Tunable

topological charge vortex microlaser. _Science_ 368, 760–763 (2020). Article  ADS  CAS  PubMed  Google Scholar  * Chen, W., Kaya Özdemir, Ş., Zhao, G., Wiersig, J. & Yang, L. Exceptional

points enhance sensing in an optical microcavity. _Nature_ 548, 192–196 (2017). Article  ADS  CAS  PubMed  Google Scholar  * Hodaei, H. et al. Enhanced sensitivity at higher-order

exceptional points. _Nature_ 548, 187–191 (2017). Article  ADS  CAS  PubMed  Google Scholar  * Hokmabadi, M. P., Schumer, A., Christodoulides, D. N. & Khajavikhan, M. Non-Hermitian ring

laser gyroscopes with enhanced Sagnac sensitivity. _Nature_ 576, 70–74 (2019). Article  ADS  PubMed  Google Scholar  * Lai, Y.-H., Lu, Y.-K., Suh, M.-G., Yuan, Z. & Vahala, K.

Observation of the exceptional-point-enhanced Sagnac effect. _Nature_ 576, 65–69 (2019). Article  ADS  CAS  PubMed  Google Scholar  * Kononchuk, R., Cai, J., Ellis, F., Thevamaran, R. &

Kottos, T. Exceptional-point-based accelerometers with enhanced signal-to-noise ratio. _Nature_ 607, 697–702 (2022). Article  ADS  CAS  PubMed  Google Scholar  * Suntharalingam, A.,

Fernández-Alcázar, L., Kononchuk, R. & Kottos, T. Noise resilient exceptional-point voltmeters enabled by oscillation quenching phenomena. _Nat. Commun._ 14, 5515 (2023). Article  ADS 

CAS  PubMed  PubMed Central  Google Scholar  * Roy, A., Jahani, S., Langrock, C., Fejer, M. & Marandi, A. Spectral phase transitions in optical parametric oscillators. _Nat. Commun._ 12,

835 (2021). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Schumer, A. et al. Topological modes in a laser cavity through exceptional state transfer. _Science_ 375, 884–888

(2022). Article  ADS  CAS  PubMed  Google Scholar  * Fu, H. & Haken, H. Multifrequency operations in a short-cavity standing-wave laser. _Phys. Rev. A_ 43, 2446–2454 (1991). Article  ADS

  CAS  PubMed  Google Scholar  * Türeci, H. E., Stone, A. D. & Collier, B. Self-consistent multimode lasing theory for complex or random lasing media. _Phys. Rev. A_ 74, 043822 (2006).

Article  ADS  Google Scholar  * Türeci, H. E., Ge, L., Rotter, S. & Stone, A. D. Strong interactions in multimode random lasers. _Science_ 320, 643–646 (2008). Article  ADS  PubMed 

Google Scholar  * Ge, L., Chong, Y. D. & Stone, A. D. Steady-state ab initio laser theory: generalizations and analytic results. _Phys. Rev. A_ 82, 063824 (2010). Article  ADS  Google

Scholar  * Esterhazy, S. et al. Scalable numerical approach for the steady-state ab initio laser theory. _Phys. Rev. A_ 90, 023816 (2014). Article  ADS  Google Scholar  * Ge, L., Tandy, R.

J., Stone, A. D. & Türeci, H. E. Quantitative verification of ab initio self-consistent laser theory. _Opt. Express_ 16, 16895–16902 (2008). Article  ADS  PubMed  Google Scholar  *

Cundiff, S. T. & Ye, J. Colloquium: femtosecond optical frequency combs. _Rev. Mod. Phys._ 75, 325–342 (2003). Article  ADS  CAS  Google Scholar  * Del’Haye, P. et al. Optical frequency

comb generation from a monolithic microresonator. _Nature_ 450, 1214–1217 (2007). Article  ADS  PubMed  Google Scholar  * Kippenberg, T. J., Gaeta, A. L., Lipson, M. & Gorodetsky, M. L.

Dissipative Kerr solitons in optical microresonators. _Science_ 361, eaan8083 (2018). Article  PubMed  Google Scholar  * Parriaux, A., Hammani, K. & Millot, G. Electro-optic frequency

combs. _Adv. Opt. Photon._ 12, 223–287 (2020). Article  Google Scholar  * Hugi, A., Villares, G., Blaser, S., Liu, H. C. & Faist, J. Mid-infrared frequency comb based on a quantum

cascade laser. _Nature_ 492, 229–233 (2012). Article  ADS  CAS  PubMed  Google Scholar  * Silvestri, C., Qi, X., Taimre, T., Bertling, K. & Rakić, A. D. Frequency combs in quantum

cascade lasers: An overview of modeling and experiments. _APL Photonics_ 8, 020902 (2023). Article  ADS  CAS  Google Scholar  * Opačak, N. et al. Nozaki–Bekki solitons in semiconductor

lasers. _Nature_ 625, 685–690 (2024). Article  ADS  PubMed  Google Scholar  * Zaitsev, O. & Deych, L. Diagrammatic semiclassical laser theory. _Phys. Rev. A_ 81, 023822 (2010). Article 

ADS  Google Scholar  * Malik, O., Makris, K. G. & Türeci, H. E. Spectral method for efficient computation of time-dependent phenomena in complex lasers. _Phys. Rev. A_ 92, 063829 (2015).

Article  ADS  Google Scholar  * Ge, L. & El-Ganainy, R. Nonlinear modal interactions in parity-time (PT) symmetric lasers. _Sci. Rep._ 6, 24889 (2016). Article  ADS  CAS  PubMed  PubMed

Central  Google Scholar  * Teimourpour, M. H., Khajavikhan, M., Christodoulides, D. N. & El-Ganainy, R. Robustness and mode selectivity in parity-time (PT) symmetric lasers. _Sci. Rep._

7, 10756 (2017). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Kominis, Y., Choquette, K. D., Bountis, A. & Kovanis, V. Exceptional points in two dissimilar coupled diode

lasers. _Appl. Phys. Lett._ 113, 081103 (2018). Article  ADS  Google Scholar  * Horstman, L., Hsu, N., Hendrie, J., Smith, D. & Diels, J.-C. Exceptional points and the ring laser

gyroscope. _Photon. Res._ 8, 252–256 (2020). Article  Google Scholar  * Bai, K. et al. Nonlinearity-enabled higher-order exceptional singularities with ultra-enhanced signal-to-noise ratio.

_Natl. Sci. Rev._ 10, nwac259 (2022). Article  PubMed  PubMed Central  Google Scholar  * Drong, M. et al. Spin vertical-cavity surface-emitting lasers with linear gain anisotropy: prediction

of exceptional points and nontrivial dynamical regimes. _Phys. Rev. A_ 107, 033509 (2023). Article  ADS  CAS  Google Scholar  * Bai, K. et al. Nonlinear exceptional points with a complete

basis in dynamics. _Phys. Rev. Lett._ 130, 266901 (2023). Article  ADS  MathSciNet  CAS  PubMed  Google Scholar  * Ji, K. et al. Tracking exceptional points above laser threshold. _Nat.

Commun._ 14, 8304 (2023). * Benzaouia, M., Stone, A. D. & Johnson, S. G. Nonlinear exceptional-point lasing with ab initio Maxwell-Bloch theory. _APL Photonics_ 7, 121303 (2022). Article

  ADS  CAS  Google Scholar  * Haken, H. _Laser Light Dynamics_ (North-Holland, 1985). * Hess, O. & Kuhn, T. Maxwell-Bloch equations for spatially inhomogeneous semiconductor lasers. I.

Theoretical formulation. _Phys. Rev. A_ 54, 3347–3359 (1996). Article  ADS  CAS  PubMed  Google Scholar  * Sauvan, C., Wu, T., Zarouf, R., Muljarov, E. A. & Lalanne, P. Normalization,

orthogonality, and completeness of quasinormal modes of open systems: the case of electromagnetism [invited]. _Opt. Express_ 30, 6846–6885 (2022). Article  ADS  CAS  PubMed  Google Scholar 

* El-Ganainy, R., Khajavikhan, M. & Ge, L. Exceptional points and lasing self-termination in photonic molecules. _Phys. Rev. A_ 90, 013802 (2014). Article  ADS  Google Scholar  * Boyd,

R. W. _Nonlinear Optics_ (Academic Press, 2020). * Petermann, K. Calculated spontaneous emission factor for double-heterostructure injection lasers with gain-induced waveguiding. _IEEE J.

Quantum Electron._ 15, 566–570 (1979). Article  ADS  MathSciNet  Google Scholar  * Siegman, A. E. Excess spontaneous emission in non-Hermitian optical systems. I. Laser amplifiers. _Phys.

Rev. A_ 39, 1253–1263 (1989). Article  ADS  CAS  Google Scholar  * Wenzel, H., Bandelow, U., Wunsche, H.-J. & Rehberg, J. Mechanisms of fast self pulsations in two-section DFB lasers.

_IEEE J. Quantum Electron._ 32, 69–78 (1996). Article  ADS  CAS  Google Scholar  * Berry, M. V. Mode degeneracies and the Petermann excess-noise factor for unstable lasers. _J. Mod. Opt._

50, 63–81 (2003). Article  ADS  CAS  Google Scholar  * Lee, S.-Y. et al. Divergent Petermann factor of interacting resonances in a stadium-shaped microcavity. _Phys. Rev. A_ 78, 015805

(2008). Article  ADS  Google Scholar  * Pick, A. et al. General theory of spontaneous emission near exceptional points. _Opt. Express_ 25, 12325–12348 (2017). Article  ADS  PubMed  Google

Scholar  * Wang, H., Lai, Y.-H., Yuan, Z., Suh, M.-G. & Vahala, K. Petermann-factor sensitivity limit near an exceptional point in a Brillouin ring laser gyroscope. _Nat. Commun._ 11,

1610 (2020). Article  ADS  PubMed  PubMed Central  Google Scholar  * Smith, D. D., Chang, H., Mikhailov, E. & Shahriar, S. M. Beyond the Petermann limit: prospect of increasing sensor

precision near exceptional points. _Phys. Rev. A_ 106, 013520 (2022). Article  ADS  CAS  Google Scholar  * Burkhardt, S., Liertzer, M., Krimer, D. O. & Rotter, S. Steady-state ab initio

laser theory for fully or nearly degenerate cavity modes. _Phys. Rev. A_ 92, 013847 (2015). Article  ADS  Google Scholar  * Liu, D. et al. Symmetry, stability, and computation of degenerate

lasing modes. _Phys. Rev. A_ 95, 023835 (2017). Article  ADS  Google Scholar  * Strogatz, S. H. _Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and

Engineering_ 2nd edn (CRC Press, 2015) * Gao, X., He, H., Sobolewski, S. & Hsu, C. W. Ab initio theory for exceptional-point lasers and periodic-inversion lasers. In _2023 Conference on

Lasers and Electro-Optics (CLEO)_ (2023). * Gao, X., He, H., Sobolewski, S. & Hsu, C. W. Frequency comb generation with lasers near exceptional points. In _Optica Nonlinear Optics

Topical Meeting 2023_ (2023). * Sweeney, W. R., Hsu, C. W., Rotter, S. & Stone, A. D. Perfectly absorbing exceptional points and chiral absorbers. _Phys. Rev. Lett._ 122, 093901 (2019).

Article  ADS  CAS  PubMed  Google Scholar  * Aspnes, D. E., Kelso, S. M., Logan, R. A. & Bhat, R. Optical properties of AlGaAs. _J. Appl. Phys._ 60, 754–767 (1986). Article  ADS  CAS 

Google Scholar  * Yao, J., Agrawal, G. P., Gallion, P. & Bowden, C. M. Semiconductor laser dynamics beyond the rate-equation approximation. _Opt. Commun._ 119, 246–255 (1995). Article 

ADS  CAS  Google Scholar  * Yu, Y., Xue, W., Semenova, E., Yvind, K. & Mork, J. Demonstration of a self-pulsing photonic crystal Fano laser. _Nat. Photon._ 11, 81–84 (2017). Article  ADS

  CAS  Google Scholar  * Zhang, J. et al. A phonon laser operating at an exceptional point. _Nat. Photon._ 12, 479–484 (2018). Article  ADS  CAS  Google Scholar  * Zhang, M. et al. Quantum

noise theory of exceptional point amplifying sensors. _Phys. Rev. Lett._ 123, 180501 (2019). Article  ADS  CAS  PubMed  Google Scholar  * Henry, C. Theory of spontaneous emission noise in

open resonators and its application to lasers and optical amplifiers. _J. Lightwave Technol._ 4, 288–297 (1986). Article  ADS  Google Scholar  * Pick, A., Cerjan, A. & Johnson, S. G. Ab

initio theory of quantum fluctuations and relaxation oscillations in multimode lasers. _J. Opt. Soc. Am. B_ 36, C22–C40 (2019). Article  CAS  Google Scholar  Download references

ACKNOWLEDGEMENTS We thank M. Khajavikhan, A. D. Stone, L. Ge, S. G. Johnson, and M. Yu for helpful discussions. This work was supported by the National Science Foundation CAREER award

(ECCS-2146021) and the University of Southern California. A.C. acknowledges support from the US Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and

Engineering. This work was performed, in part, at the Center for Integrated Nanotechnologies, an Office of Science User Facility operated by the US Department of Energy (DOE) Office of

Science. Sandia National Laboratories is a multimission laboratory managed and operated by National Technology & Engineering Solutions of Sandia, LLC, a wholly-owned subsidiary of

Honeywell International, Inc., for the US DOE’s National Nuclear Security Administration under contract DE-NA-0003525. The views expressed in the article do not necessarily represent the

views of the US DOE or the United States Government. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Ming Hsieh Department of Electrical and Computer Engineering, University of Southern

California, Los Angeles, CA, 90089, USA Xingwei Gao, Hao He, Scott Sobolewski & Chia Wei Hsu * Center for Integrated Nanotechnologies, Sandia National Laboratories, Albuquerque, NM,

87185, USA Alexander Cerjan Authors * Xingwei Gao View author publications You can also search for this author inPubMed Google Scholar * Hao He View author publications You can also search

for this author inPubMed Google Scholar * Scott Sobolewski View author publications You can also search for this author inPubMed Google Scholar * Alexander Cerjan View author publications

You can also search for this author inPubMed Google Scholar * Chia Wei Hsu View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS X.G. developed

the theory on the _ζ_ factor, stability analysis, PALT, integral equation solver, and performed the SALT and PALT calculations. H.H., assisted by A.C., developed the FDTD code. X.G., H.H.,

and S.S. performed the FDTD simulations. H.H. developed the spectral analysis of the FDTD results. C.W.H. conceived of the project. C.W.H. and A.C. supervised the project. C.W.H. and X.G.

wrote the paper with inputs from the other coauthors. All authors discussed the results. CORRESPONDING AUTHORS Correspondence to Xingwei Gao or Alexander Cerjan. ETHICS DECLARATIONS

COMPETING INTERESTS The authors declare no competing interests. PEER REVIEW PEER REVIEW INFORMATION _Nature Communications_ thanks Qinghui Yan, and the other, anonymous, reviewer(s) for

their contribution to the peer review of this work. A peer review file is available. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional

claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION PEER REVIEW FILE RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed

under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate

credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article

are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and

your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this

licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Gao, X., He, H., Sobolewski, S. _et al._ Dynamic gain and frequency

comb formation in exceptional-point lasers. _Nat Commun_ 15, 8618 (2024). https://doi.org/10.1038/s41467-024-52957-4 Download citation * Received: 08 April 2024 * Accepted: 26 September 2024

* Published: 04 October 2024 * DOI: https://doi.org/10.1038/s41467-024-52957-4 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable

link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative