Excited state non-adiabatic dynamics of large photoswitchable molecules using a chemically transferable machine learning potential

ABSTRACT Light-induced chemical processes are ubiquitous in nature and have widespread technological applications. For example, photoisomerization can allow a drug with a photo-switchable

scaffold such as azobenzene to be activated with light. In principle, photoswitches with desired photophysical properties like high isomerization quantum yields can be identified through

virtual screening with reactive simulations. In practice, these simulations are rarely used for screening, since they require hundreds of trajectories and expensive quantum chemical methods

to account for non-adiabatic excited state effects. Here we introduce a _diabatic artificial neural network_ (DANN), based on diabatic states, to accelerate such simulations for azobenzene

derivatives. The network is six orders of magnitude faster than the quantum chemistry method used for training. DANN is transferable to azobenzene molecules outside the training set,

predicting quantum yields for unseen species that are correlated with experiment. We use the model to virtually screen 3100 hypothetical molecules, and identify novel species with high

predicted quantum yields. The model predictions are confirmed using high-accuracy non-adiabatic dynamics. Our results pave the way for fast and accurate virtual screening of photoactive

compounds. SIMILAR CONTENT BEING VIEWED BY OTHERS CHARTING ELECTRONIC-STATE MANIFOLDS ACROSS MOLECULES WITH MULTI-STATE LEARNING AND GAP-DRIVEN DYNAMICS VIA EFFICIENT AND ROBUST ACTIVE

LEARNING Article Open access 13 May 2025 MOLECULAR EXCITED STATES THROUGH A MACHINE LEARNING LENS Article 20 May 2021 DEEP-NEURAL-NETWORK SOLUTION OF THE ELECTRONIC SCHRÖDINGER EQUATION

Article 23 September 2020 INTRODUCTION Light is a powerful tool for manipulating molecular systems. It can be controlled with high spatial, spectral and temporal precision to facilitate a

variety of processes, including energy transfer, intermolecular reactions, and photoisomerization1. These processes are used in areas as diverse as synthesis, energy storage, display

technology, biological imaging, diagnostics and medicine1,2,3. Photoactive drugs, for instance, are photoswitchable compounds whose bioactivity can be toggled through light-induced

isomerization. Precise spatiotemporal control of bioactivity allows photoactive drugs to be delivered in high doses with minimal off-target activity and side effects. Such therapeutics are a

promising path for the treatment of cancer, neurodegenerative diseases, bacterial infections, diabetes, and blindness4,5. Theory plays a key role in explaining and predicting photochemistry

because empirical heuristics learned from thermally activated ground state processes typically do not apply to excited states3. Computer simulations based on quantum mechanics can achieve

impressive accuracy in the prediction of experimental observables. These include the isomerization efficiency and absorption spectrum of photoswitchable compounds6, which are key quantities

in the design of photoactive drugs. However, ab initio methods in photochemistry are severely limited by their computational cost7. In order to gather meaningful statistics for one molecule,

hundreds of replicate simulations are needed, each of which involves thousands of electronic structure calculations performed in series with sub-femtosecond timesteps. The individual

quantum chemical calculations are particularly demanding, requiring excited state gradients and some treatment of multireference effects. In some cases, both the ground and excited state

gradients are required at each time step8,9. Using ab initio methods to compute photochemical properties of tens or hundreds molecules is impractical, and photodynamic simulations have not

yet been used for large-scale virtual screening. Among the most accurate and expensive electronic structure methods are multireference perturbation techniques10,11,12,13,14,15, but their

cost and requirement for manual active space selection limit their use in virtual screening. The photochemistry community has made exciting developments over several years to overcome both

of these hurdles. For example, reduced scaling techniques16,17 and graphics processing units18 can significantly accelerate multi-reference calculations. The density matrix renormalization

group (DMRG)19,20 and multi-reference density functional theory (DFT) methods21,22,23 have expanded the size of systems that can be treated with high accuracy. DMRG has also been used to

automate the selection of active spaces for multi-reference methods24,25. Less accurate but more affordable black-box methods include spin-flip time-dependent DFT (SF-TDDFT)26 and hole-hole

Tamm-Dancoff DFT27, among others28,29,30,31,32,33. Despite these developments, the cost of non-adiabatic simulations remains high. As discussed below, even SF-TDDFT is prohibitively

expensive for virtual screening. Semi-empirical methods34,35,36 are currently the only affordable approach for large-scale screening. They provide qualitatively correct results across many

systems, but are ultimately bounded by their approximations, with average energy errors of 15 kcal/mol35. A different approach is to use data-driven models in place of quantum chemistry (QC)

calculations. Machine learning (ML) models trained on quantum chemical data can now routinely predict ground state energies and forces with sub-chemical accuracy37,38,39, and take only

milliseconds to make predictions. These models have been successfully used in a variety of ground state simulations38,40,41. They have also been used to accelerate non-adiabatic simulations

in a number of model systems42,43,44,45,46,47,48. However, excited state ML has not yet offered affordable photodynamics for hundreds of molecules of realistic size, which is the ultimate

goal for predictive simulation in photopharmacology. Further, no excited state interatomic potentials have been developed that are transferable to different compounds. They therefore require

thousands of QC calculations for every new species to serve as training data. Here we make significant progress toward affordable, large-scale photochemical simulations and virtual

screening with ML. To develop a transferable potential we focus on molecules from the same chemical family, studying derivatives of azobenzene, a prototypical photoswitch. The derivatives

studied here contain up to 100 atoms, making them the largest systems fit with excited state ML potentials to date. Combining an equivariant neural network38 and a physics-informed diabatic

model, together with data generated by combinatorial exploration of chemical space, and configurational sampling through active learning, we produce a model that is transferable to large,

unseen derivatives of azobenzene. This yields computational savings in excess of six orders of magnitude. Predicted isomerization quantum yields of unseen species are correlated with

experimental values. The model is used to predict the quantum yield for over 3100 hypothetical species, revealing rare molecules with high _cis_-to-_trans_ and _trans_-to-_cis_ quantum

yields. RESULTS AZOBENZENE PHOTOSWITCHES This work focuses on the photoswitching of azobenzene derivatives, but the methods are general and can be applied to other chemistries and other

excited state processes. Azobenzene derivatives can exist as _cis_ or _trans_ isomers. The conformations are local minima in the ground state, but not in the excited state. Photoexcitation

of either can therefore induce isomerization into the other (see the potential energy schematics in Figs. 1(a) and 2(b)). A key experimental observable is the quantum yield, defined as the

probability that excitation leads to isomerization. The yield depends critically on the dynamics near conical intersections (CIs), configurations in which the excitation energy is zero. In

these regions the electrons can return to the ground state with non-zero probability. Many approaches have been developed over several decades to model such non-adiabatic transitions. These

include ab initio multiple spawning49 and cloning50; Ehrenfest dynamics8,9; coherent switching with decay of mixing51; the variantional multi-configurational Gaussian method52; exact

factorization53,54,55,56,57; the multi-configuration time-dependent Hartree (MCTDH) method58,59; Gaussian MCTDH60; and trajectory surface hopping61. A recent review of these methods can be

found in ref. 3. Surface hopping is a popular approach because of its simplicity and efficiency. In this method, independent trajectories are simulated with stochastic hops between potential

energy surfaces (PESs). Depending on the curvature of the PESs and the location of the hop, a trajectory can end in the original isomer or in a new isomer (Figs. 1(a) and 2(b)). The quantum

yield is the proportion of trajectories that end in a new isomer. Our goal is to predict the quantum yield of azobenzene derivatives after excitation from the singlet ground state (_S_0) to

the first singlet excited state (_S_1). This can be accomplished with the surface hopping approach described above, using a fast surrogate ML model to generate the PESs. The impact of

considering only the first excited state is discussed in Supplementary Note 3. ML ARCHITECTURE AND TRAINING Our model is based on the PaiNN neural network38, which uses equivariant

message-passing to predict molecular properties. In this approach, an initial feature vector is generated for each atom using its atomic number. The vector is then updated through a set of

neural network operations involving “messages”, which incorporate the distance, orientation, and features of atoms within a cutoff distance. A series of updates leads to information being

aggregated from increasingly distant atoms. Once the updates are complete, the atomic features are mapped to molecular energies using a neural network. This architecture can be used to

predict energies and, through automatic differentiation, the forces for each state. However, models that predict adiabatic energies have a basic shortcoming for non-adiabatic molecular

dynamics (NAMD). Since surface hopping is largely controlled by the energy gap when it is close to zero, small errors in the energies can lead to exponentially large errors in the hopping

probability62,63. This in turn can cause large errors in observable quantities like the quantum yield. This point is discussed in further detail in Supplementary Methods A. Further, since

CIs are non-differentiable cusps in the energy gap, they are difficult to fit with neural networks. For _N_ atoms in a molecule, the network must predict two different energies that are

exactly equal in 3_N_ − 8 dimensions. We found this to be particularly challenging for _trans_ species that are outside the training set. As shown in Supplementary Note 6, small errors in

the gap lead to the incorrect prediction that many species never hop to the ground state. To remedy this issue we introduce a model based on diabatic states, which we call DANN (diabatic

artificial neural network; Fig. 2(a)). The approach builds on previous work using neural networks for diabatization64,65,66. Much of the previous work could only be used for specific system

types, such as semi-rigid molecules65 and coupled monomers, and is thus not applicable to azobenzene. None of the methods have been used for large systems with significant conformational

changes64,66, such as azobenzene derivatives. Further, our work uses diabatization to ease the fitting of adiabatic states across chemical space. In particular, it addresses the issue of gap

overestimation near conical intersections of unseen species, as described in Supplementary Notes 1 and 6. Our work uses diabatization to address this problem, whereas previous work only

used diabatization in single, model species. We also note that gap overestimation in unseen species is both a newly-identified and newly-addressed problem, as previous work in ML-NAMD

focused on single species only42,43,44,45,46,47,48. The diabatic energies form a non-diagonal Hamiltonian matrix, \({{{\mathbf{H}}}}_{d}\), which is diagonalized to yield adiabatic energies.

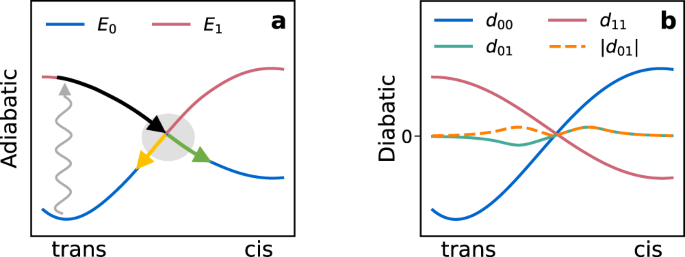
When a 2 × 2 sub-block of \({{{\mathbf{H}}}}_{d}\) has diagonal elements that cross, and off-diagonal elements that pass through zero, a CI cusp is generated (Fig. 1). The diabatic energies

that generate the cusp are smooth, which makes them easier to fit with an interpolating function than the adiabatic energies. In the DANN architecture, smoothness is imposed through a loss

function related to the non-adiabatic coupling vector (NACV). The loss minimizes the value that the NACV takes when it is rotated from the adiabatic basis (Eq. (3)) into the diabatic basis.

The NACV measures the change in overlap between two wavefunctions after a small nuclear displacement. If the NACV between two states is zero, then their wavefunctions must change slowly in

response to a nuclear perturbation. Therefore, their energies cannot form the cusp in Fig. 1(a), and must instead resemble the smooth energies in Fig. 1(b). The DANN model was trained on

SF-TDDFT26 calculations for 567,037 geometries, using the 6-31G* basis67 and BHHLYP68 exchange-correlation functional. Unlike traditional TDDFT69, SF-TDDFT provides an accurate description

of the CI region70, and, unlike multi-reference methods, is fairly fast and requires no manual parameter selection. The configurations were sampled from 8,269 azobenzene derivatives, of

which 164 were taken from the experimental literature. The remaining molecules were generated from combinatorial substitution using common literature patterns (Supplementary Tables X and

XI). The data generation process is shown in Fig. 2. Initial data was generated through ab initio NAMD with 164 species from the literature, together with normal-mode sampling and

distortions of the combinatorial species to near-CI regions. The remaining data was generated through active learning. In each cycle we trained a committee of models, used one model to

perform NN-NAMD, and used the committee variance and energy gap to choose NAMD geometries for new quantum chemistry calculations. The cycle was repeated five times in total; further details

can be found in the Methods section. VALIDATION To test whether the model could reproduce experimental results for unseen molecules, we evaluated it on species that were outside the training

set. The test set contained 40 species (20 _cis_/_trans_ pairs), including 33 with experimental _S_1 quantum yields in non-polar solution. Non-polar solution was chosen because it is the

closest to the gas-phase conditions simulated here. Solvent effects can be easily incorporated into the model through transfer learning to implicit solvent calculations. This was previously

shown to require new calculations for only a small proportion of the training set40. The performance of the model is summarized in Table 1. Statistics are shown for both seen and unseen

species. The former contains species that are in the training set, but geometries that are outside of it. The geometries were selected with the balanced sampling criteria described in

Supplementary Note 9. Geometries from unseen species were generated with DANN-NAMD using the final trained model. Half of the DANN-NAMD geometries were selected randomly from the full

trajectory and half by proximity to a CI (Supplementary Eq. (13)). 100 configurations were chosen for each molecule. For species in the training set, all quantities are accurate to within

approximately 1 kcal/mol(/Å). Apart from the NACV, all quantities have _R_2 correlation coefficients close to 1. The _R_2 of the NACV is 0.84. This may be somewhat low because diabatization

cannot remove the curl component of the NACV in the diabatic basis71,72. This would also explain the low _R_2 value for the NACV in ref. 45, which computed it as the gradient of a scalar.

For molecules outside the training set, all quantities apart from the energies have an error below 3 kcal/mol(/Å). The energy gaps and ground state forces have _R_2 correlation coefficients

near 1. The gap error of 1.89 kcal/mol should be contrasted with the error of 15 kcal/mol for the semi-empirical method in ref. 35. The errors in the excited state forces are slightly

larger, but still quite low. The correlation coefficient for the force NACV \({\overrightarrow{h}}_{01}\) is rather poor. As described in Supplementary Note 6, the yields of _trans_

derivatives are better correlated with experiment when using Zhu-Nakamura surface hopping than Tully’s method. The latter uses the NACV and the former does not, so part of the difference may

be explained by the high error in the force NACV. Nevertheless, there is still reasonable agreement between Tully’s method and experiment, suggesting that errors in the force NACV do not

spoil the dynamics. Figure 3(a) shows snapshots from an example DANN-NAMD trajectory, and panel (b) shows random samples of the hopping geometries. Reactive hopping geometries are shown on

top, and non-reactive ones are shown below. The molecule is the (aminomethyl)pyridine derivative 26, with the species numbering given in Supplementary Data 2 and 3. The overlays show

_cis_-_trans_ isomerization proceeding through inversion-assisted rotation, consistent with previous work73. The dominant motion is rotation, with the CNNC dihedral angle increasing in

magnitude from −10∘ at equilibrium to −86∘ at the hopping points. Significant changes also occur in the CNN and NNC angles, with each transitioning from 123∘ to either 113∘ or 135∘. The

predicted PES in the branching space \((\overrightarrow{g},\overrightarrow{h})\) is shown beside the geometries. \(\overrightarrow{h}\) is the direction of the force NACV and

\(\overrightarrow{g}\propto {\nabla }_{R}({{\Delta }}{E}_{01})\) is the direction of the gap gradient. Each vector was computed with automatic differentiation using Eq. (1). The diabatic

energies, adiabatic energies, and gap are shown from top to bottom. We see that the model generates a true CI, in which the _S_0 and _S_1 energies are exactly equal. Further, the degeneracy

is lifted in both the \(\overrightarrow{g}\)- and \(\overrightarrow{h}\)-directions, so that the _S_1 energy and gap each form a characteristic cone. These hallmarks of CIs are built into

the model because the adiabatic energies are eigenvalues of a diabatic matrix. For example, the cone emerges from the fact that _d_11 − _d_00 and _d_01 each pass linearly through zero in

different directions74. Figure 3(c) indicates that the predicted and experimental quantum yields of unseen species are correlated. The yields are for the 33 _cis_ and _trans_ species with

experimental data in Supplementary Data 1. The _R_2 value is 0.42, and the Spearman rank correlation coefficient _ρ_ is 0.74. While the _R_2 value is somewhat low, the Spearman rank

correlation is high. The Spearman coefficient measures the accuracy with which the model ranks species by quantum yield. _ρ_ only compares orderings, while _R_2 compares the model error to

the error of a mean predictor. This means that _ρ_ is a more forgiving metric, and also a more relevant metric for virtual screening. Since _cis_ isomers have yields two to three times

higher than _trans_ isomers, the high value of _ρ_ means that the model properly separates the isomers into low- and high-yield groups. Further, as shown in Supplementary Figs. 5 and 7, the

model produces meaningful rankings among _trans_ species. The correlation coefficients are _ρ_ = 0.32 using Tully’s method61 and _ρ_ = 0.57 using the Zhu-Nakamura approach75. The model is

largely able to differentiate between high- and low-yield _trans_ derivatives. Several such molecules are of interest. They are color-coded in the plots, with the legend given below. A full

list of predictions is given in Supplementary Data 1. We see, for example, that the (aminomethyl)pyridine derivatives 1 and 35 are both predicted to have near-zero yields. These species do

not isomerize from _trans_ to _cis_, because strong N-H hydrogen bonds lock the planar _trans_ conformation in place76. Replacing the NH group in 1 with N - CH3 gives species 25. This

molecule isomerizes because there is no hydrogen bonding. This, too, is predicted by the model. Further, the hepta-tert-butyl derivative 17 has an experimental and predicted yield of zero.

This is likely because of steric interactions among the bulky tert-butyl groups. While able to account for these two different mechanisms, the model fails to predict the subtle electronic

effects in species 11 and 29. Resonance interactions between oxygen lone pairs and the azo group modify the PES, such that there is no rotational CI77. There is instead a concerted inversion

CI, which occurs too early along the path between _trans_ and _cis_ to allow for isomerization. The changes in the PES may either be too small or too specific to the substituents for the

model to predict without fine tuning. Finally, derivatives with high yields are partly distinguished from those with low but non-zero yields. An example is 21, whose experimental yield of

10% is half that of _trans_-azobenzene. The model properly identifies this molecule as having a low yield, but also mistakenly does the same for several high-yield species. The accuracy for

unseen species could always be improved with transfer learning, in which the model is fine-tuned with a small number of calculations from a single molecule (discussed below). This would

increase the computational cost, but would still be orders of magnitude less expensive than ab initio NAMD. While meaningful correlations are produced for _trans_ species, the same is not

true of _cis_ molecules (_ρ_ = 0.02). This may be because there are no _cis_ derivatives with zero yield. Nevertheless, the model properly identifies 20 as having the highest yield. Further,

it does not mistakenly assign a zero yield to any derivative. This is noteworthy because, as shown in Fig. 4(a) and (b), some hypothetical _cis_ species are predicted to have zero yield.

Synthesis of non-switching _cis_ derivatives and comparison to predictions could therefore be of interest in the future. Overall, we observe moderate correlation between predicted and

experimental yields. The Spearman correlation is high when including both isomers, moderate for _trans_ isomers, and low for _cis_ isomers. The _R_2 value, a measure of numerical error

compared to that of a mean predictor, is moderate when including both isomers and near-zero when separating them. Indeed, the MAEs of the mean predictor are 9.5%, 10.3%, and 17.7% for

_trans_, _cis_, and all species, respectively. The model MAEs before (after) subtracting the mean signed error are 14.4% (13.5%), 11.5% (11.2%) and 13.2% (13.0%). In addition to model error,

sources of error include inaccuracies in SF-TDDFT, approximations in surface hopping, solvent effects, and experimental uncertainty. These are discussed in depth in Supplementary Note 3.

Each source of error affects both _R_2 and _ρ_, but is expected to have a larger effect on _R_2. The rank correlation with experiment is encouraging given the difficulty of the task, as

captured by the sensitivity of the yield to model errors in the PES75, and given the sources of error outside the model. Further, as discussed below, DANN provides an excellent starting

point for fine-tuned, molecule-specific models that can be used for high-accuracy simulations of single species. Figure 3(d) shows that DANN-NAMD is extremely fast. The plot shows the node

time, defined as _t_calc/_n_calc, where _t_calc is the calculation time per geometry, and _n_calc is the number of parallel calculations that can be performed on a single node. We see that

ML speeds up calculations by five to six orders of magnitude. The direct comparison of the pre-trained model node times and QC node times is appropriate because the model generalizes to

unseen species. This means that it incurs no extra QC cost for any future simulations. The minimum speedup corresponds to the smallest molecules (14 heavy atoms or 24 total atoms), and the

maximum to the largest molecules (70 heavy atoms or 99 total atoms). This reflects the different scaling of the QC and ML calculations. Empirically we see that DANN scales as _N_0.49 for _N_

heavy atoms, while SF-TDDFT scales as _N_2.8. These values come from fitting the timings to _t_ = _A_ ⋅ _N__x_, where _t_ is the computational time, _A_ and _x_ are fitted constants, and

_N_ is the number of heavy atoms. DANN’s apparent sub-linear scaling is an artifact of diagonalizing \({{{\mathbf{H}}}}_{d}\); when the diagonalization is removed, the scaling becomes

linear. This is the expected scaling for a message-passing neural network with a fixed cutoff radius. Evidently diagonalizing \({{{\mathbf{H}}}}_{d}\) introduces a large overhead with weak

dependence on system size. Nevertheless, we see that DANN is still quite fast. VIRTUAL SCREENING Having shown that the model is fast and generalizes in the chemical and configurational space

of azobenzenes, we next used it for virtual screening of hypothetical compounds. We first retrained the network on all available data, including species that were originally held out, for a

total of 631,367 geometries in the training set. We then predicted the quantum yields of 3100 combinatorial species generated through literature-informed substitution patterns, as in ref.

78. This screen served two purposes. The first was to gather statistics about the distribution of photophysical properties of azobenzenes at a scale not accessible to experiments or

traditional simulations. The second was to identify molecules with rare desirable properties. In particular, we sought to find molecules with high _c_ → _t_ or _t_ → _c_ quantum yields and

redshifted absorption spectra. The former is important because increasing the ratio QY_a_→_b_/QY_b_→_a_, where QY is the quantum yield, can lead to more complete _a_ → _b_ transformation

under steady state illumination. This is critical for precise spatial control of drug activity when the two isomers have different biological effects79. Redshifting is a crucial requirement

for photo-active drugs, since human tissue is transparent only in the near-IR79. The results are shown in Fig. 4. Panels (a) and (c) show the predicted yield vs. mean gap. For each species

we averaged the gap over the configurations sampled during neural network ground state MD. The thermal averaging led to a typical blueshift of 0.2–0.3 eV relative to the gaps of single

equilibrium geometries. The mean excitation energies are 2.95 eV for _cis_ derivatives and 2.84 eV for _trans_ species; the gaps are 2.98 eV and 2.97 eV for the respective unsubstituted

compounds. The average gaps and their differences are similar to experimental measurements for azobenzene80. The average _c_ → _t_ and _t_ → _c_ yields are 54% and 24%, respectively, while

those of the unsubstituted species are 59% and 37%. These are consistent with experimental results in non-polar solution, for which the base compound has yields of 44–55% and 23–28%80; the

former is closer to 55% on average. However, the yield of the base _trans_ compound is overestimated with respect to both theory and experiment6,75,80. The mean (median) proportion of

trajectories ending in the ground state after 2 ps are 92% (100%) for _cis_ species and 31% (17%) for _trans_ species. The standard deviations are 25% and 30%, respectively. Panels (b) and

(d) show the yield plotted against the isomeric stability, defined as _E__t__r__a__n__s_ − _E__c__i__s_ for _trans_ isomers and _E__c__i__s_ − _E__t__r__a__n__s_ for _cis_ isomers. The

energy _E_ is the median value of the configurations sampled in the ground state; we used the median to reduce the effect of outlier geometries. On average the _trans_ isomers are more

stable than the _cis_ isomers by 0.66 eV (15.3 kcal/mol), which is similar to experimental values over 10 kcal/mol for azobenzene81. The stability is of interest for three reasons. First, a

large absolute value indicates that one isomer is dominant at room temperature. This is essential for photoactive drugs, and is the case for regular azobenzene. Second, an inverted

stability, in which _cis_ is more stable than _trans_, allows for stronger absorption at longer wavelengths. This is because the dipole-forbidden _n_ − _π_* (_S_1) transition is

significantly stronger for _cis_ than for _trans_80. Third, in photopharmacology, one often wants to deliver a drug in inactive form, and activate it with light in a localized region. If

_trans_ happens to be active and _cis_ inactive, then localized activation is only possible if _cis_ is more stable. Several species of interest are shown in Fig. 4. The molecules 165 and

166 have predicted _c_ → _t_ yields of 75 ± 6% and 72 ± 6%, respectively, which are well above the _cis_ average of 55%. The species 169 and 170 have predicted _t_ → _c_ yields of 66 ± 7%

and 63 ± 10%, respectively, which are three times the average _trans_ yield. Molecule 167 is highly redshifted, with a mean predicted gap of 2.26 eV (548 nm), and a standard deviation of

0.87 eV. QC calculations on the geometries sampled with DANN gave a gap of 2.26 ± 0.61 eV, in good agreement with predictions. The mean gap is lower than the median of 2.52 eV, which

reflects the presence of several ultra-low gap structures. The low gap and large variance mean that 167 may be able to absorb in the near IR. The redshifting is likely because of the six

electron donating groups, which increase the HOMO energy, together with the crowding of the four _ortho_ substituents. The latter distorts the molecule, leading to twisted configurations

with smaller gaps. Finally, species 168 is more stable in _cis_ form than _trans_ form. The predicted _cis_ stability is − 0.79 eV (−18 kcal/mol), in good agreement with the QC prediction of

−0.92 eV (−21 kcal/mol). As mentioned above, this inverted stability can be a desirable property for photopharmacology. To validate the yield results, we performed DANN-NAMD using highly

accurate species-specific models. As described in Supplementary Note 13 B, we generated a model for each species by refining the base network with data from that species alone. The data was

generated through several active learning cycles, resulting in 1200–2500 training geometries for each compound. We used this approach in place of ab initio NAMD because of the latter’s

prohibitive cost for large molecules. The QC computational cost for fine-tuning was at most 3% of that of an ab initio simulation, and hence far less demanding. The average gradient

calculation for a molecule with 50 atoms took 58 min for two surfaces using 8 cores, and the average NACV calculation took 55 min. Fine-tuning with 2000 geometries for a medium-sized

molecule would thus take 30,000 core hours. For ab initio NAMD, a conservative estimate of 100 trajectories run for 1 ps each, with only one gradient computed per frame, would take 780,000

core hours. We also computed the yields of _cis_ and _trans_ azobenzene for comparison. For these species we used full ab initio simulations, because of the central role of the unsubstituted

compound as a reference point and because simulations were fairly affordable for such small molecules. Issues with spin contamination also hampered the fine-tuning process for these

compounds (see Supplementary Note 13 B). Initially we generated refined models for species 165, 166, 169 and 170. It became clear early on that only 165 and 169 had high yields, and so we

focused on those molecules thereafter. Using molecule-specific models, we computed the quantum yields of 165 and 169 to be 66 ± 1% and 37 ± 1%, respectively. The computed yields for _cis_

and _trans_ azobenzene are 60 ± 4% and 26 ± 3%, respectively, which are in excellent agreement with experiment80. Both of the new molecules have higher quantum yields than the associated

base compounds. The improvement is particularly large for species 169: its yield is 11 points higher than _trans_ azobenzene, which is a relative enhancement of 42 percent. We show below

that that this significant increase has an intuitive physical explanation. The dynamics of the four molecules are shown in Fig. 5. Panels (a) and (b) show the CNNC dihedral angle vs. time

for azobenzene, and panels (d) and (e) show the same for the derivatives. Both the substituted and unsubstituted _cis_ isomers rapidly proceed through a rotational CI, but the derivative

rotates much more quickly. Indeed, we see that the isomerization of the derivative is complete within 75 fs, while the base compound takes nearly 130 fs. The excited state lifetimes are 34.2

 ± 0.3 fs and 63 ± 3 fs for the derivative and base compound, respectively, indicating that the former reaches the CI earlier than the latter. These observations may explain the enhanced

yield, since a higher rotational velocity leads to more efficient isomerization82. We also note that the derivative rotates in only the counter-clockwise direction, while _cis_ azobenzene

rotates in both directions, but this is not expected to affect the yield. The two _trans_ molecules behave in qualitatively different ways. In _trans_ azobenzene, the distribution of

dihedral angles slowly widens with time (Fig. 5(b)). This is consistent with a rotational barrier6,75, as different trajectories overcome the barrier at different times, and so the torsion

angle becomes uniformly distributed. Additionally, as seen in the marginal dihedral distribution of Fig. 5(c), many of the geometries hop near 180∘. This agrees with ref. 6, which identified

a non-reactive planar CI and a reactive twisted CI as the main hopping points for _trans_ azobenzene. The non-reactive CI leads exclusively back to _trans_, while the reactive CI leads to

_cis_ and _trans_ in different proportions. Using the method described in Supplementary Note 13 C, we found that 26% of the trajectories proceed through the planar CI and 74% through the

rotational CI. This is similar to the distribution reported in ref. 75. Approximately 36% of the rotational trajectories generate _cis_ azobenzene, giving an overall yield of 26%. This is in

good agreement with previous computational and experimental values6. By contrast, nearly all trajectories of 169, including non-reactive trajectories, rotate significantly. This can be seen

in the marginal dihedral distribution in Fig. 5(f), in which the hops are tightly localized around 180 ± 77∘. Only 5% of the trajectories hop at the planar CI, which is five times lower

than the base compound. Additionally, the yield of the rotational trajectories increases from 36 to 40%. The inhibition of the planar CI pathway, together with the enhancement of the

rotational yield, leads to an overall yield increase from 26 to 37%. While the enhanced reactive yield does not have a simple explanation, the reason for the planar pathway inhibition can be

clearly seen in Fig. 5(e). Whereas the rotation of 51 is stochastic, leading to a uniform distribution of angles, the rotation of 169 is initially concerted. Nearly all trajectories rotate

in unison to a dihedral angle of 180 ± 45∘ at 300 fs. Past 300 fs, hopping begins and the trajectories separate from each other. Hence they proceed through the rotational reactive CI, and

become distributed between 0∘ and 360∘ after hopping. The planar non-reactive CI is avoided because of the molecule’s initial rotation. This explanation is consistent with the presence of

bulky _ortho_ groups, which twist the equilibrium structure and hence weaken the N=N double bond. This lowers the excited state barrier to rotation, which leads to an initial torsion and

hence increases the yield. DISCUSSION The DANN model shows high accuracy and transferability among azobenzene derivatives. One limitation is that the unseen species contained functional

groups that were present to some degree in the training set. Model performance was generally higher for more highly represented functional groups, though some groups were highly represented

yet difficult to fit, while others were weakly represented and well-fit (Supplementary Note 4). Moreover, the model cannot be applied to other chemical families without additional training

data. Further, as shown in Supplementary Note 6, it substantially overestimates the excited state lifetime for a number of _trans_ derivatives. On the other hand, semi-empirical methods

provide qualitatively correct predictions across a variety of chemistries, but cannot match DANN’s in-domain accuracy, and cannot be improved with more reference data. Adding features from

semi-empirical calculations, as done in the OrbNet model83, may therefore prove useful in the future. Recent developments accounting for non-local effects and spin states have improved

neural network transferability39, and could also be beneficial for excited states. The model could be further improved with high-accuracy multi-reference calculations, solvent effects, and

the inclusion of the bright _S_2 state. The use of spin-complete methods in particular is of crucial importance, since spin contamination prevented fine-tuning the model for the base

compounds. It may also have affected the accuracy of the DANN model in general. Thus spin-complete, affordable alternatives are of particular interest27. Active learning could be accelerated

through differentiable sampling with adversarial uncertainty attacks84, which would improve the excited state lifetimes. Transfer learning could also be used to improve performance for

specific molecules. Only a small number of ab initio calculations would be required to fine-tune the model for an individual species. Diabatization may also prove to be useful for reactive

ground states. Reaction barriers can often be understood as transitions from one diabatic state to another85. The diabatic basis may make reactive surfaces easier to fit with neural

networks. In conclusion, we have introduced a diabatic multi-state neural network potential trained on over 630,000 geometries at the SF-TDDFT BHHLYP/6-31G* level of theory, covering over

8000 unique azobenzene molecules. We used DANN-NAMD to predict the isomerization quantum yields of derivatives outside the training set, and the results were correlated with experiment. We

also identified several hypothetical compounds with high quantum yields, redshifted excitation energies, and inverted stabilities. The network architecture, diabatization approach, and

chemical and configurational diversity of the training data allowed us to produce a robust and transferable potential. The model can be applied off-the-shelf to new molecules, producing

results that approximate those of SF-TDDFT at orders of magnitude lower computational cost. METHODS NETWORK AND TRAINING As explained in Supplementary Methods A, a unique challenge for

non-adiabatic simulations is their sensitivity to the energy difference between states. Using a typical neural network to predict energies and forces for NAMD leads to some molecules

becoming incorrectly trapped in the excited state. This is partly caused by overestimation of the gap and/or an incorrectly shaped PES in the vicinity of the CI. To address this issue we

introduce an architecture based on diabatic states, whose smooth variation leads to more accurate neural network fitting (Fig. 1(b)). In general diabatic states must satisfy86

$${\left({{{{{{{{\bf{U}}}}}}}}}^{{{{\dagger}}} }\left[{\nabla

}_{R}{{{\mathbf{H}}}}_{d}\right]{{{{{{{\bf{U}}}}}}}}\right)}_{nm}=\left\{\begin{array}{l}-{\overrightarrow{f}}_{n},{{{{{{{\rm{if}}}}}}}}\ n=m\\

{\overrightarrow{h}}_{nm},{{{{{{{\rm{if}}}}}}}}\ n\,\ne\, m.\end{array}\right.$$ (1) where ∇_R_ is the gradient with respect to \(\overrightarrow{R}\), U diagonalizes the diabatic

Hamiltonian through $${\left({{{{{{{{\bf{U}}}}}}}}}^{{{{\dagger}}} }{{{\mathbf{H}}}}_{d}{{{{{{{\bf{U}}}}}}}}\right)}_{nm}={E}_{n}{\delta }_{nm},$$ (2) and \({\overrightarrow{f}}_{n}=-{\nabla

}_{R}{E}_{n}\) is the adiabatic force for the _n_th state. The dependence on \(\overrightarrow{R}\) has been suppressed for ease of notation. \({\overrightarrow{h}}_{nm}\) is the force

NACV, $${\overrightarrow{h}}_{nm}(\overrightarrow{R}) =\left\langle {\psi }_{n}(\overrightarrow{r};\overrightarrow{R})\left|{\nabla

}_{R}\hat{H}(\overrightarrow{r},\overrightarrow{R})\right|{\psi }_{m}(\overrightarrow{r};\overrightarrow{R})\right\rangle \\

=({E}_{m}(\overrightarrow{R})-{E}_{n}(\overrightarrow{R}))\,{\overrightarrow{k}}_{nm}(\overrightarrow{R}),$$ (3) where \(\hat{H}(\overrightarrow{r},\overrightarrow{R})\) is the clamped

nucleus Hamiltonian, \({\psi }_{n}(\overrightarrow{r};\overrightarrow{R})\) is the _n_th adiabatic wavefunction, and the matrix element is an integral over the electronic degrees of freedom

\(\overrightarrow{r}\). The vector \({\overrightarrow{k}}_{nm}(\overrightarrow{R})\) is the derivative coupling: $${\overrightarrow{k}}_{nm}(\overrightarrow{R})=\left\langle {\psi

}_{n}(\overrightarrow{r};\overrightarrow{R})\left|\right.{\nabla }_{R}{\psi }_{m}(\overrightarrow{r};\overrightarrow{R})\right\rangle$$ (4) Combined with the following reference geometry

conditions (Supplementary Methods C), $$\begin{array}{l}({E}_{0},\,{E}_{1})=\left\{\begin{array}{ll}({d}_{00},\,{d}_{11}), &{{{{{{{\rm{if}}}}}}}}\overrightarrow{R}\in trans\\

({d}_{22},\,{d}_{00}), &{{{{{{{\rm{if}}}}}}}}\overrightarrow{R}\in cis,\end{array}\right.\end{array}$$ (5) we arrive at three sets of constraints, Eqs. (1), (2), and (5). In principle

only Eqs. (1) and (2) are required for the states to be diabatic. However, we found the reference loss to provide a minor improvement in the gap near CIs (Supplementary Table I). We use a

neural network to map the nuclear positions \({\overrightarrow{R}}_{i}\) and charges _Z__i_ to the diabatic matrix elements _d__n__m_, and a loss function to impose Eqs. (1), (2) and (5).

The adiabatic energies _E__n_ are generated by diagonalizing \({{{\mathbf{H}}}}_{d}\), and the forces and couplings by applying Eq. (1) and using automatic differentiation. The design of the

network is shown schematically in Fig. 2(a). The general form of the diabatic loss function is

$${{{{{{{\mathcal{L}}}}}}}}={{{{{{{{\mathcal{L}}}}}}}}}_{{{{{{{{\rm{core}}}}}}}}}+{{{{{{{{\mathcal{L}}}}}}}}}_{{{{{{{{\rm{ref}}}}}}}}}+{{{{{{{{\mathcal{L}}}}}}}}}_{{{{{{{{\rm{nacv}}}}}}}}}.$$

(6) Here \({{{{{{{{\mathcal{L}}}}}}}}}_{{{{{{{{\rm{core}}}}}}}}}\) penalizes errors in the adiabatic energies, forces, and gaps, \({{{{{{{{\mathcal{L}}}}}}}}}_{{{{{{{{\rm{ref}}}}}}}}}\)

imposes Eq. (5) and \({{{{{{{{\mathcal{L}}}}}}}}}_{{{{{{{{\rm{nacv}}}}}}}}}\) imposes Eq. (1) for _n_ ≠ _m_. The terms are defined explicitly in Supplementary Eqs. (1)–(3). For the network

itself we adopt the PaiNN equivariant architecture38. In this approach a set of scalar and vector features for each atom are iteratively updated through a series of convolutions (Fig. 2(a)).

In the message block, the features of each atom gather information from atoms within a cutoff distance, using the interatomic displacements. The scalar and vector features for each atom are

then mixed in the update phase. Hyperparameters can be found in Supplementary Table IV. Most were taken from ref. 38, but some were modified based on experiments with azobenzene geometries.

Further details of the PaiNN model can be found in ref. 38. Once the elements of \({{{\mathbf{H}}}}_{d}\) are generated, the diabatic matrix is diagonalized to yield the transformation

matrix U and the adiabatic energies _E__n_. The vector quantities \({\overrightarrow{f}}_{n}\) and \({\overrightarrow{h}}_{nm}\) are given by Eq. (1). When non-adiabatic couplings are not

required, the \({\overrightarrow{f}}_{n}\) can be calculated by directly differentiating the _E__n_. This is more efficient than Eq. (1), since it requires only _M_ad = 2 < _M_d(_M_d + 

1)/2 = 6 gradient calculations. This approach was used for NAMD runs, which required only diabatic energies, adiabatic energies, and adiabatic forces, while Eq. (1) was used for training.

DATA GENERATION AND ACTIVE LEARNING Data was generated in two different ways. First, we searched the literature for azobenzene derivatives that had been synthesized and tested

experimentally. This yielded 164 species (82 _cis_ and 82 _trans_). For these species we performed ab initio NAMD, yielding geometries that densely sampled configurational space. Second, to

enhance chemical diversity, we generated nearly 10,000 species through combinatorial azobenzene substitution. This was done using 48 common literature substituents and four common

substitution patterns (Supplementary Tables X and XI). We then performed geometry optimizations, normal mode sampling, and inversion/rotation about the central N=N bond to generate

configurations. QC calculations were performed on 25,212 combinatorial geometries. All calculations were performed with Q-Chem 5.387, using SF-TDDFT26 with the BHHLYP functional68 and 6-31G*

basis67. Two neural networks were trained on the initial data and used to perform DANN-NAMD. Initial positions and velocities for DANN-NAMD were generated from classical MD with the

Nosé-Hoover thermostat88,89. The initial trajectories were unstable because the networks had not been trained on high-energy configurations. To address this issue we used active

learning40,41 to iteratively improve the network predictions (Fig. 2(b)). After each trajectory we performed new QC calculations on a sample of the generated geometries. For all but the last

two rounds of active learning, geometries were selected according to the variance in predictions of two different networks, where the networks were initialized with different parameters and

trained with different random batches. In the last two rounds, half the geometries were selected by network variance, and half by proximity to a CI. Further details are given in

Supplementary Note 12. The new data was then added to the training set and used to retrain the networks. The cycle was repeated three times with all species and another two times with

azobenzene alone. In all, we computed ground state gradients, excited state gradients, and NACVs with SF-TDDFT for 641,367 geometries. 96% of the geometries were from the 164 literature

species. In total, 88% were generated through ab initio NAMD and 8% through active learning. The remaining 4% were from the combinatorial species. 1.5% were generated through geometry

optimizations, 1.5% through inversion/rotation, and 1% through normal-mode sampling. We initially set out to train a model using energies and forces alone. Since analytic NACVs are

unavailable for many ab initio methods, an adiabatic architecture could have been used with a wider variety of methods. NACVs also add computational overhead, and so generating training data

for an adiabatic model would have taken less time. To this end we initially used the Zhu-Nakamura (ZN) surface hopping method82, which only requires adiabatic energies and forces. However,

the issues with adiabatic models described in Supplementary Note 6 led us to develop the diabatic approach. Since diabatic states can be used with any surface hopping method, we used the

diabatic model to perform Tully’s fewest switches (FS) surface hopping61 after the last round of active learning. All results in the main text use the FS method. A comparison of FS and ZN

results is given in Supplementary Note 6. DATA AVAILABILITY The quantum chemistry data generated in this study has been deposited in the Materials Data Facility database at

https://doi.org/10.18126/unc8-336t. A detailed description of how to load and interpret the data is given in the README file. Source data of experimental and predicted quantum yields are

provided in the Supplementary Information/Source Data file. CODE AVAILABILITY Trained models and computer code are available in the Neural Force Field repository at

https://github.com/learningmatter-mit/NeuralForceField. Notebook tutorials explain how to train the models and perform DANN-NAMD. REFERENCES * Evans, R. C., Douglas, P. & Burrow, H. D.

_Applied photochemistry_ (Springer, 2013). * Kolpak, A. M. & Grossman, J. C. Azobenzene-functionalized carbon nanotubes as high-energy density solar thermal fuels. _Nano Lett._ 11,

3156–3162 (2011). Article  ADS  CAS  PubMed  Google Scholar  * Mai, S. & González, L. Molecular photochemistry: Recent developments in theory. _Angewandte Chemie Int. Ed_ 59, 16832–16846

(2020). Article  CAS  Google Scholar  * Broichhagen, J., Frank, J. A. & Trauner, D. A roadmap to success in photopharmacology. _Acc. Chem. Res._ 48, 1947–1960 (2015). Article  CAS 

PubMed  Google Scholar  * Lerch, M. M., Hansen, M. J., van Dam, G. M., Szymanski, W. & Feringa, B. L. Emerging targets in photopharmacology. _Angewandte Chemie Int. Edition_ 55,

10978–10999 (2016). Article  CAS  Google Scholar  * Yu, J. K., Bannwarth, C., Liang, R., Hohenstein, E. G. & Martínez, T. J. Nonadiabatic dynamics simulation of the wavelength-dependent

photochemistry of azobenzene excited to the n_π_* and _π__π_* excited states. _J. Am. Chem. Soc._ 142, 20680–20690 (2020). Article  CAS  PubMed  Google Scholar  * Bannwarth, C., Yu, J. K.,

Hohenstein, E. G. & Martínez, T. J. Hole–hole Tamm–Dancoff-approximated density functional theory: A highly efficient electronic structure method incorporating dynamic and static

correlation. _J. Chem. Phys._ 153, 024110 (2020). Article  PubMed  CAS  Google Scholar  * Tully, J. C. Mixed quantum–classical dynamics. _Faraday Discussions_ 110, 407–419 (1998). Article 

ADS  CAS  Google Scholar  * Shalashilin, D. V. Quantum mechanics with the basis set guided by Ehrenfest trajectories: Theory and application to spin-boson model. _J Chem. Phys._ 130, 244101

(2009). Article  ADS  PubMed  CAS  Google Scholar  * Nakano, H. Quasidegenerate perturbation theory with multiconfigurational self-consistent-field reference functions. _J. Chem. Phys._ 99,

7983–7992 (1993). Article  ADS  CAS  Google Scholar  * Finley, J., Malmqvist, P., Roos, B. O. & Serrano-Andrés, L. The multi-state CASPT2 method. _Chem. Phys. Lett._ 288, 299–306 (1998).

Article  ADS  CAS  Google Scholar  * Angeli, C., Cimiraglia, R., Evangelisti, S., Leininger, T. & Malrieu, J.-P. Introduction of n-electron valence states for multireference

perturbation theory. _J. Chem. Phys._ 114, 10252–10264 (2001). Article  ADS  CAS  Google Scholar  * Malmqvist, P. A., Pierloot, K., Shahi, A. R. M., Cramer, C. J. & Gagliardi, L. The

restricted active space followed by second-order perturbation theory method: Theory and application to the study of CuO2 and

\({{{{{{{{\rm{C{u}}}}}}}_{2}{{\rm{O}}}}}}_{{{{{{{{\rm{2}}}}}}}}}\) systems. _J. Chem. Phys._ 128, 204109 (2008). Article  ADS  PubMed  CAS  Google Scholar  * Shiozaki, T., Győrffy, W.,

Celani, P. & Werner, H.-J. Communication: Extended multi-state complete active space second-order perturbation theory: Energy and nuclear gradients. _J. Chem. Phys._ 135, 081106–081106

(2011). Article  ADS  PubMed  CAS  Google Scholar  * Ma, D., Manni, G. L., Olsen, J. & Gagliardi, L. Second-order perturbation theory for generalized active space self-consistent-field

wave functions. _J. Chem. Theory Comput._ 12, 3208–3213 (2016). Article  CAS  PubMed  Google Scholar  * Song, C. & Martínez, T. J. Reduced scaling extended multi-state CASPT2

(XMS-CASPT2) using supporting subspaces and tensor hyper-contraction. _J. Chem. Phys._ 152, 234113 (2020). Article  ADS  CAS  PubMed  Google Scholar  * Song, C., Neaton, J. B. &

Martínez, T. J. Reduced scaling formulation of CASPT2 analytical gradients using the supporting subspace method. _J. Chem. Phys._ 154, 014103 (2021). Article  ADS  CAS  PubMed  Google

Scholar  * Seritan, S. et al. TeraChem: Accelerating electronic structure and ab initio molecular dynamics with graphical processing units. _J. Chem. Phys._ 152, 224110 (2020). Article  ADS

  CAS  PubMed  PubMed Central  Google Scholar  * Marti, K. H. & Reiher, M. New electron correlation theories for transition metal chemistry. _Phys. Chem. Chem. Phys._ 13, 6750–6759

(2011). Article  CAS  PubMed  Google Scholar  * Sharma, S. & Chan, G. K.-L. Spin-adapted density matrix renormalization group algorithms for quantum chemistry. _J. Chem. Phys._ 136,

124121 (2012). Article  ADS  PubMed  CAS  Google Scholar  * Marian, C. M., Heil, A. & Kleinschmidt, M. The DFT/MRCI method. _Wiley Interdisciplinary Rev.: Comput. Mol. Sci._ 9, e1394

(2019). Google Scholar  * Manni, G. L. et al. Multiconfiguration pair-density functional theory. _J. Chem. Theory Comput._ 10, 3669–3680, 2014. * Gagliardi, L. et al. Multiconfiguration

pair-density functional theory: A new way to treat strongly correlated systems. _Acc. Chem. Res._ 50, 66–73 (2017). Article  CAS  PubMed  Google Scholar  * Stein, C. J. & Reiher, M.

Automated selection of active orbital spaces. _J. Chem. Theory Comput._ 12, 1760 (2016). Article  CAS  PubMed  Google Scholar  * Stein, C. J. & Reiher, M. autoCAS: A program for fully

automated multiconfigurational calculations. _J. Comput. Chem,_ 40, 2216 (2019). CAS  Google Scholar  * Shao, Y., Head-Gordon, M. & Krylov, A. I. The spin–flip approach within

time-dependent density functional theory: Theory and applications to diradicals. _J. Chem. Phys._ 118, 4807–4818 (2003). Article  ADS  CAS  Google Scholar  * Yu, J. K., Bannwarth, C.,

Hohenstein, E. G. & Martínez, T. J. Ab initio nonadiabatic molecular dynamics with hole–hole Tamm–Dancoff approximated density functional theory. _J. Chem. Theory Comput._ 16, 5499–5511

(2020). Article  CAS  PubMed  Google Scholar  * Li, S. L., Marenich, A. V., Xu, X. & Truhlar, D. G. Configuration interaction-corrected Tamm–Dancoff approximation: A time-dependent

density functional method with the correct dimensionality of conical intersections. _J. Phys. Chem. Lett._ 5, 322–328 (2014). Article  CAS  PubMed  Google Scholar  * Filatov, M.

Spin-restricted ensemble-referenced Kohn–Sham method: basic principles and application to strongly correlated ground and excited states of molecules. _Wiley Interdisciplinary Rev.: Comput.

Mol. Sci._ 5, 146–167 (2015). CAS  Google Scholar  * Yang, Y., Shen, L., Zhang, D. & Yang, W. Conical intersections from particle–particle random phase and Tamm–Dancoff approximations.

_J. Phys. Chem. Lett._ 7, 2407–2411 (2016). Article  CAS  PubMed  PubMed Central  Google Scholar  * Shu, Y., Parker, K. A. & Truhlar, D. G. Dual-functional Tamm–Dancoff approximation: a

convenient density functional method that correctly describes _S_1/_S_0 conical intersections. _J. Phys. Chem. Lett._ 8, 2107–2112 (2017). Article  CAS  PubMed  Google Scholar  * Lee, S.,

Filatov, M., Lee, S. & Choi, C. H. Eliminating spin-contamination of spin-flip time dependent density functional theory within linear response formalism by the use of zeroth-order

mixed-reference (MR) reduced density matrix. _J. Chem. Phys._ 149, 104101 (2018). Article  ADS  PubMed  CAS  Google Scholar  * Teh, H.-H. & Subotnik, J. E. The simplest possible approach

for simulating _S_0–_S_1 conical intersections with DFT/TDDFT: Adding one doubly excited configuration. _J. Phys. Chem. Lett._ 10, 3426–3432 (2019). Article  CAS  PubMed  Google Scholar  *

Cusati, T. et al. Semiempirical Hamiltonian for simulation of azobenzene photochemistry. _J. Phys. Chem. A_ 116, 98–110 (2012). Article  CAS  PubMed  Google Scholar  * Inamori, M.,

Yoshikawa, T., Ikabata, Y., Nishimura, Y. & Nakai, H. Spin-flip approach within time-dependent density functional tight-binding method: Theory and applications. _J. Comput. Chem._ 41,

1538–1548 (2020). Article  CAS  PubMed  Google Scholar  * de Wergifosse, M., Bannwarth, C. & Grimme, S. A simplified spin-flip time-dependent density functional theory approach for the

electronic excitation spectra of very large diradicals. _J. Phys. Chem. A_ 123, 5815–5825 (2019). Article  PubMed  CAS  Google Scholar  * Qiao, Z., Welborn, M., Anandkumar, A., Manby, F. R.

& Miller III, T. F. OrbNet: Deep learning for quantum chemistry using symmetry-adapted atomic-orbital features. _J. Chem. Phys._ 153, 124111 (2020). Article  ADS  CAS  PubMed  Google

Scholar  * Schütt, K., Unke, O. & Gastegger, M. Equivariant message passing for the prediction of tensorial properties and molecular spectra. In _International Conference on Machine

Learning_, 9377-9388. PMLR, (2021). * Unke, O. T. et al. Spookynet: Learning force fields with electronic degrees of freedom and nonlocal effects. _Nat. Commun._ 12, 1–14 (2021). Article 

CAS  Google Scholar  * Ang, S. J., Wang, W., Schwalbe-Koda, D., Axelrod, S. & Gómez-Bombarelli, R. Active learning accelerates ab initio molecular dynamics on reactive energy surfaces.

_Chem_ 7, 738 (2021). Article  CAS  Google Scholar  * Wang, W., Yang, T., Harris, W. H. & Gómez-Bombarelli, R. Active learning and neural network potentials accelerate molecular

screening of ether-based solvate ionic liquids. _Chem. Commun._ 56, 8920 (2020). Article  CAS  Google Scholar  * Chen, W.-K., Liu, X.-Y., Fang, W.-H., Dral, P. O. & Cui, G. Deep learning

for nonadiabatic excited-state dynamics. _J. Phys. Chem. Lett._ 9, 6702–6708 (2018). Article  CAS  PubMed  Google Scholar  * Dral, P. O., Barbatti, M. & Thiel, W. Nonadiabatic

excited-state dynamics with machine learning. _J. Phys. Chem. Lett._ 9, 5660–5663 (2018). Article  CAS  PubMed  PubMed Central  Google Scholar  * Hu, D., Xie, Y., Li, X., Li, L. & Lan,

Z. Inclusion of machine learning kernel ridge regression potential energy surfaces in on-the-fly nonadiabatic molecular dynamics simulation. _J. Phys. Chem. Lett._ 9, 2725–2732 (2018).

Article  CAS  PubMed  Google Scholar  * Li, J. et al. Automatic discovery of photoisomerization mechanisms with nanosecond machine learning photodynamics simulations. _Chem. Sci._ 12,

5302–5314 (2021). * Westermayr, J. Machine learning enables long time scale molecular photodynamics simulations. _Chem. Sci._ 10, 8100–8107 (2019). Article  CAS  PubMed  PubMed Central 

Google Scholar  * Westermayr, J., Gastegger, M. & Marquetand, P. Combining SchNet and SHARC: The SchNarc machine learning approach for excited-state dynamics. _J. Phys. Chem. Lett._ 11,

3828–3834 (2020). Article  CAS  PubMed  PubMed Central  Google Scholar  * Westermayr, J. & Marquetand, P. Machine learning for electronically excited states of molecules. _Chem. Rev._

121, 9873–9926 (2020). Article  PubMed  PubMed Central  CAS  Google Scholar  * Ben-Nun, M., Quenneville, J. & Martínez, T. J. Ab initio multiple spawning: Photochemistry from first

principles quantum molecular dynamics. _J. Phys. Chem. A_ 104, 5161–5175 (2000). Article  CAS  Google Scholar  * Makhov, D. V., Glover, W. J., Martinez, T. J. & Shalashilin, D. V. Ab

initio multiple cloning algorithm for quantum nonadiabatic molecular dynamics. _J. Chem. Phys._ 141, 054110 (2014). Article  ADS  PubMed  CAS  Google Scholar  * Zhu, C., Nangia, S., Jasper,

A. W. & Truhlar, D. G. Coherent switching with decay of mixing: an improved treatment of electronic coherence for non-Born–Oppenheimer trajectories. _J. Chem. Phys._ 121, 7658–7670

(2004). Article  ADS  CAS  PubMed  Google Scholar  * Richings, G. W. et al. Quantum dynamics simulations using Gaussian wavepackets: the vMCG method. _Int. Rev. Phys. Chem._ 34, 269–308

(2015). Article  CAS  Google Scholar  * Abedi, A., Maitra, N. T. & Gross, E. K. U. Exact factorization of the time-dependent electron-nuclear wave function. _Phys. Rev. Lett._ 105,

123002 (2010). Article  ADS  PubMed  CAS  Google Scholar  * Abedi, A., Agostini, F. & Gross, E. K. U. Mixed quantum-classical dynamics from the exact decomposition of electron-nuclear

motion. _EPL Europhys. Lett._ 106, 33001 (2014). Article  ADS  CAS  Google Scholar  * Min, S. K., Agostini, F., Tavernelli, I. & Gross, E. K. U. Ab initio nonadiabatic dynamics with

coupled trajectories: A rigorous approach to quantum (de) coherence. _J. Phys. Chem. Lett._ 8, 3048–3055 (2017). Article  CAS  PubMed  Google Scholar  * Curchod, B. F. E. & Agostini, F.

On the dynamics through a conical intersection. _J. Phys. Chem. Lett._ 8, 831–837 (2017). Article  CAS  PubMed  Google Scholar  * Ha, J.-K., Lee, I. S. & Min, S. K. Surface hopping

dynamics beyond nonadiabatic couplings for quantum coherence. _J. Phys. Chem. Lett._ 9, 1097–1104 (2018). Article  CAS  PubMed  Google Scholar  * Beck, M. H., Jäckle, A., Worth, G. A. &

Meyer, H.-D. The multiconfiguration time-dependent Hartree (MCTDH) method: a highly efficient algorithm for propagating wavepackets. _Phys. Rep._ 324, 1–105 (2000). Article  ADS  CAS  Google

Scholar  * Wang, H. & Thoss, M. Multilayer formulation of the multiconfiguration time-dependent Hartree theory. _J. Chem. Phys._ 119, 1289–1299 (2003). Article  ADS  CAS  Google Scholar

  * Burghardt, I., Meyer, H.-D. & Cederbaum, L. S. Approaches to the approximate treatment of complex molecular systems by the multiconfiguration time-dependent Hartree method. _J. Chem.

Phys._ 111, 2927–2939 (1999). Article  ADS  CAS  Google Scholar  * Tully, J. C. Molecular dynamics with electronic transitions. _J. Chem. Phys._ 93, 1061–1071 (1990). Article  ADS  CAS 

Google Scholar  * Zhu, C. & Nakamura, H. The two-state linear curve crossing problems revisited. II. Analytical approximations for the Stokes constant and scattering matrix: The

Landau–Zener case. _J. Chem. Phys._ 97, 8497–8514 (1992). Article  ADS  CAS  Google Scholar  * Zhu, C. & Nakamura, H. The two-state linear curve crossing problems revisited. III.

Analytical approximations for Stokes constant and scattering matrix: Nonadiabatic tunneling case. _J. Chem. Phys._ 98, 6208–6222 (1993). Article  ADS  CAS  Google Scholar  * Shu, Y. &

Truhlar, D. G. Diabatization by machine intelligence. _J. Chem. Theory Comput._ 16, 6456–6464 (2020). Article  CAS  PubMed  Google Scholar  * Williams, D. M. G. & Eisfeld, W. Neural

network diabatization: A new ansatz for accurate high-dimensional coupled potential energy surfaces. _J. Chem. Phys._ 149, 204106 (2018). Article  ADS  PubMed  CAS  Google Scholar  * Guan,

Y., Zhang, D. H., Guo, H. & Yarkony, D. R. Representation of coupled adiabatic potential energy surfaces using neural network based quasi-diabatic Hamiltonians: 1,2 \({}^{2}A^{\prime}\)

states of LiFH. _Phys. Chem. Chem. Phys._ 21, 14205–14213 (2019). Article  CAS  PubMed  Google Scholar  * Francl, M. M. et al. Self-consistent molecular orbital methods. XXIII. A

polarization-type basis set for second-row elements. _J. Chem. Phys._ 77, 3654–3665 (1982). Article  ADS  CAS  Google Scholar  * Becke, A. D. A new mixing of Hartree–Fock and local

density-functional theories. _J. Chem. Phys._ 98, 1372–1377 (1993). Article  ADS  CAS  Google Scholar  * Levine, B. G., Ko, C., Quenneville, J. & Martínez, T. J. Conical intersections

and double excitations in time-dependent density functional theory. _Mol. Phys._ 104, 1039–1051 (2006). Article  ADS  CAS  Google Scholar  * Lee, S., Shostak, S., Filatov, M. & Choi, C.

H. Conical intersections in organic molecules: Benchmarking mixed-reference spin–flip time-dependent DFT (MRSF-TD-DFT) vs spin–flip TD-DFT. _J. Phys. Chem. A_ 123, 6455–6462 (2019). Article

  CAS  PubMed  Google Scholar  * Mead, C. A. & Truhlar, D. G. Conditions for the definition of a strictly diabatic electronic basis for molecular systems. _J. Chem. Phys._ 77, 6090–6098

(1982). Article  ADS  CAS  Google Scholar  * Baer, M. & Englman, R. A study of the diabatic electronic representation within the Born-Oppenheimer approximation. _Mol. Phys._ 75, 293–303

(1992). Article  ADS  CAS  Google Scholar  * Toniolo, A., Ciminelli, C., Persico, M. & Martínez, T. J. Simulation of the photodynamics of azobenzene on its first excited state:

Comparison of full multiple spawning and surface hopping treatments. _J. Chem. Phys._ 123, 234308 (2005). Article  ADS  CAS  PubMed  Google Scholar  * Köppel, H., Gronki, J. & Mahapatra,

S. Construction scheme for regularized diabatic states. _J. Chem. Phys._ 115, 2377 (2001). Article  ADS  CAS  Google Scholar  * Yue, L., Liu, Y. & Zhu, C. Performance of TDDFT with and

without spin-flip in trajectory surface hopping dynamics: cis_⇌_trans azobenzene photoisomerization. _Phys. Chem. Chem. Phys._ 20, 24123–24139 (2018). Article  CAS  PubMed  Google Scholar  *

Bandara, H. M. D. et al. Proof for the concerted inversion mechanism in the trans → cis isomerization of azobenzene using hydrogen bonding to induce isomer locking. _J. Organic Chem._ 75,

4817–4827 (2010). Article  CAS  Google Scholar  * Bandara H. M. D., Cawley S., Gascón A, & Burdette S. C. Short-circuiting azobenzene photoisomerization with electron-donating

substituents and reactivating the photochemistry with chemical modification. _ Eur. J. Org. Chem._ 2011, 2916–2919 (2011). * Gómez-Bombarelli, R. et al. Design of efficient molecular organic

light-emitting diodes by a high-throughput virtual screening and experimental approach. _Nat. Mater._ 15, 1120–1127 (2016). Article  ADS  PubMed  CAS  Google Scholar  * Velema, W. A.,

Szymanski, W. & Feringa, B. L. Photopharmacology: beyond proof of principle. _J. Am. Chem. Soc._ 136, 2178–2191 (2014). Article  CAS  PubMed  Google Scholar  * Bandara, H. M. D. &

Burdette, S. C. Photoisomerization in different classes of azobenzene. _Chem. Soc. Revi._ 41, 1809–1825 (2012). Article  CAS  Google Scholar  * Dias, A. R. et al. Enthalpies of formation of

cis-azobenzene and trans-azobenzene. _J. Chem. Thermodyn._ 24, 439–447 (1992). Article  CAS  Google Scholar  * Yu, L., Xu, C., Lei, Y., Zhu, C. & Wen, Z. Trajectory-based nonadiabatic

molecular dynamics without calculating nonadiabatic coupling in the avoided crossing case: Trans_⇌_cis photoisomerization in azobenzene. _Phys. Chem. Chem. Phys._ 16, 25883–25895 (2014).

Article  CAS  PubMed  Google Scholar  * Qiao, Z. et al. Multi-task learning for electronic structure to predict and explore molecular potential energy surfaces. arXiv preprint

arXiv:2011.02680 (2020). * Schwalbe-Koda, D., Tan, A. R. & Gómez-Bombarelli, R. Differentiable sampling of molecular geometries with uncertainty-based adversarial attacks. _Nat. Commun._

12, 1–12 (2021). * Van Voorhis, T. et al. The diabatic picture of electron transfer, reaction barriers, and molecular dynamics. _Ann. Rev. Phys. Chem._ 61, 149–170 (2010). Article  CAS 

Google Scholar  * Schuurman, M. S. & Yarkony, D. R. On the vibronic coupling approximation: A generally applicable approach for determining fully quadratic quasidiabatic coupled

electronic state Hamiltonians. _J. Chem. Phys._ 127, 094104 (2007). Article  ADS  PubMed  CAS  Google Scholar  * Shao, Y. et al. Advances in molecular quantum chemistry contained in the

Q-Chem 4 program package. _Mol. Phys._ 113, 184–215 (2015). Article  ADS  CAS  Google Scholar  * Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. _J.

Chem. Phys._ 81, 511–519 (1984). Article  ADS  Google Scholar  * Hoover, W. G. Canonical dynamics: Equilibrium phase-space distributions. _Phys. Rev. A_ 31, 1695 (1985). Article  ADS  CAS 

Google Scholar  Download references ACKNOWLEDGEMENTS We thank Wujie Wang, Daniel Schwalbe-Koda, Shi Jun Ang (MIT), Kristof Schütt, and Oliver Unke (Technische Universität Berlin) for

scientific discussions and access to computer code. Harvard Cannon cluster, MIT Engaging cluster, and MIT Lincoln Lab Supercloud cluster at MGHPCC are gratefully acknowledged for

computational resources and support. Financial support from DARPA (Award HR00111920025) and MIT-IBM Watson AI Lab is acknowledged. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of

Chemistry and Chemical Biology, Harvard University, Cambridge, MA, 02138, USA Simon Axelrod & Eugene Shakhnovich * Department of Materials Science and Engineering, Massachusetts

Institute of Technology, Cambridge, MA, 02139, USA Simon Axelrod & Rafael Gómez-Bombarelli Authors * Simon Axelrod View author publications You can also search for this author inPubMed 

Google Scholar * Eugene Shakhnovich View author publications You can also search for this author inPubMed Google Scholar * Rafael Gómez-Bombarelli View author publications You can also

search for this author inPubMed Google Scholar CONTRIBUTIONS S.A. conceived the project, and developed the methodology with R.G.-B. and E.S. S.A. performed the calculations under the

guidance of R.G.-B. S.A. wrote the first draft of the manuscript, and all authors contributed to the final version. CORRESPONDING AUTHOR Correspondence to Rafael Gómez-Bombarelli. ETHICS

DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. PEER REVIEW PEER REVIEW INFORMATION _Nature Communications_ thanks the anonymous reviewers for their contribution

to the peer review of this work. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional

affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION DESCRIPTION OF ADDITIONAL SUPPLEMENTARY FILES SUPPLEMENTARY DATA 1 SUPPLEMENTARY DATA 2 SUPPLEMENTARY DATA 3 RIGHTS AND

PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any

medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The

images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not

included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly

from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Axelrod, S.,

Shakhnovich, E. & Gómez-Bombarelli, R. Excited state non-adiabatic dynamics of large photoswitchable molecules using a chemically transferable machine learning potential. _Nat Commun_

13, 3440 (2022). https://doi.org/10.1038/s41467-022-30999-w Download citation * Received: 27 October 2021 * Accepted: 23 May 2022 * Published: 15 June 2022 * DOI:

https://doi.org/10.1038/s41467-022-30999-w SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative