Harmonization of quality metrics and power calculation in multi-omic studies

ABSTRACT Multi-omic studies combine measurements at different molecular levels to build comprehensive models of cellular systems. The success of a multi-omic data analysis strategy depends

largely on the adoption of adequate experimental designs, and on the quality of the measurements provided by the different omic platforms. However, the field lacks a comparative description

of performance parameters across omic technologies and a formulation for experimental design in multi-omic data scenarios. Here, we propose a set of harmonized Figures of Merit (FoM) as

quality descriptors applicable to different omic data types. Employing this information, we formulate the MultiPower method to estimate and assess the optimal sample size in a multi-omics

experiment. MultiPower supports different experimental settings, data types and sample sizes, and includes graphical for experimental design decision-making. MultiPower is complemented with

MultiML, an algorithm to estimate sample size for machine learning classification problems based on multi-omic data. SIMILAR CONTENT BEING VIEWED BY OTHERS CHALLENGES AND BEST PRACTICES IN

OMICS BENCHMARKING Article 12 January 2024 UNDISCLOSED, UNMET AND NEGLECTED CHALLENGES IN MULTI-OMICS STUDIES Article 21 June 2021 CHARACTERIZING THE OMICS LANDSCAPE BASED ON 10,000+

DATASETS Article Open access 25 January 2025 INTRODUCTION The genomics research community has been increasingly proposing the parallel measurement of diverse molecular layers profiled by

different omic assays as a strategy to obtain comprehensive insights into biological systems1,2,3,4. Encouraged by constant cost reduction, data-sharing initiatives, and availability of data

(pre)processing methods5,6,7,8,9,10,11,12,13, the so-called multi-platform or multi-omics studies are becoming popular. However, the success of a multi-omic project in revealing complex

molecular interconnections strongly depends on the quality of the omic measurement and on the synergy between a carefully designed experimental setup and a suitable data integration

strategy. For example, multi-omic measurements should derive from the same samples, observations should be many, and variance distributions similar if the planned approach for data

integration relies on correlation networks. Frequently, these issues are overlooked, and analysis expectations are frustrated by underpowered experimental design, noisy measurements, and the

lack of a realistic integration method. A thorough understanding of individual omic platform properties and their influence on data integration efforts represents an important, but usually

ignored, aspect of multi-omic experiment planning. Several tools are available to assess omic data quality, even cross-platform, such as FastQC for raw sequencing (seq) reads14,

Qualimap15,16 and SAMstat17 for mapping output, and MultiQC18 that combines many different tools in a single report. However, these tools do not apply to non-sequencing omics (i.e.,

metabolomics) and are not conceived to compare platform performance nor support multi-omic experimental design choices. Figures of Merit (FoM) are performance metrics typically used in

analytical chemistry to describe devices and methods. FoM include accuracy, reproducibility, sensitivity, and dynamic range; descriptors also applied to omic technologies. However, the

definition of each FoM acquires a slightly different specification depending on the omic technology considered, and each omic platform possesses different critical FoM. For example, RNA-seq

usually provides unbiased, comprehensive coverage of the targeted space (i.e., RNA molecules), while this is not the case for shotgun proteomics, which is strongly biased toward abundant

proteins. Importantly, we currently lack both a systematic description of FoM discrepancies across omic assays and a definition of a common performance language to support discussions on the

multi-omic experimental design. FoM are relevant to statistical analyses that aim to detect differential features, due to their impact on the number of replicates required to achieve a

given statistical power. The statistical power of an analysis method, which is the ability of the method to detect true changes between experimental groups, is determined by the within-group

variability, the size of the effect to be detected, the significance level to be achieved, and the number of replicates (or observations) per experimental group, also known as sample size.

All these parameters are highly related to FoM. Estimating power in omic experiments is challenging because many features are assessed simultaneously19. These features may have different

within-condition variability and the significance level must be adapted to account for the multiple testing scenario. Deciding on the effect size to detect may also prove difficult,

especially when the natural dynamic range of the data has changed due to normalization procedures. Moreover, different omic platforms present distinct noise levels and dynamic ranges, and

hence analysis methods might not be equally applicable to all of them. As a consequence, independently computing the statistical power for each omic might not represent the best approach for

a multi-omic experiment, if the different measurements are to be analyzed in an integrative fashion and a joint power study for all platforms seems more appropriate. Although several

methods have been proposed to optimize sample size and evaluate statistical power in single-omic experiments19,20, no such tool exists in the context of multi-omics data. Similarly,

multi-omic datasets are increasingly collected to develop sample class predictors applying machine learning (ML) methods. In this case, the classification error rate (ER), rather than the

significance value, is used to assess performance. In the field of ML, the estimation of the number of samples required to achieve an established prediction error is still an open

question21,22 and there are not yet methods that answer this question for multi-omics applications. In summary, the multi-omics field currently lacks a comparative description of performance

metrics across omic technologies and methods to estimate the number of samples required for their multiple applications. In this work, we propose a formal definition of FoM applicable

across several omics and provide a common language to describe the performance of high-throughput methods frequently combined in multi-omic studies. We leverage this harmonized quality

control vocabulary to develop MultiPower, an approach for power calculations in multi-omic experiments applicable to across omics platforms and types of data. Additionally, we present

MultiML, an R method to obtain the optimal sample size required by ML approaches to achieve a target classification ER. The FoM definitions, together with the MultiPower and MultiML

calculations proposed here constitute a framework for quality control and precision in the design of multi-omic experiments. RESULTS COMPARATIVE DESCRIPTIONS OF OMIC MEASUREMENT QUALITY We

selected seven commonly used FoM that cover different quality aspects of molecular high-throughput platforms (see “Methods” section, Fig. 1, Supplementary Table 1). Figure 2 summarizes the

comparative analysis for these FoM across seven different types of omic platforms, classified as mass spectrometry (MS) based (proteomics and metabolomics) or sequencing based. In this

study, we consider short-read seq-based methods that measure genome variation and dynamic aspects of the genomes, and divided them into feature-based (RNA-seq and miRNA-seq) and region-based

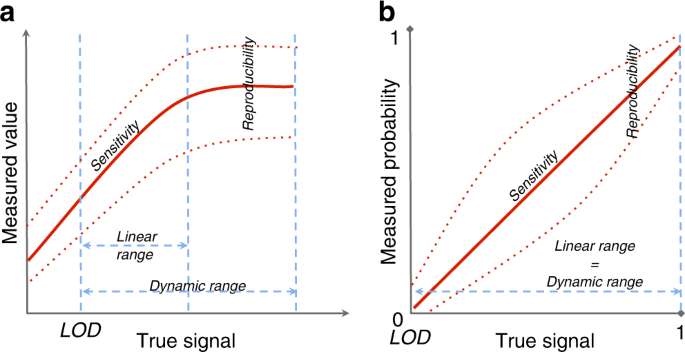
methods (DNA-seq, ChIP-seq, Methyl-seq, and ATAC-seq). Sensitivity is defined as the slope of the calibration line that compares the measured value of an analyte with the true level of that

analyte (Fig. 1). For a given platform and feature, sensitivity is the ability of the platform to distinguish small differences in the levels of that feature. Features with low sensitivity

suffer from less accurate quantification and are more difficult to be significant by differential analysis methods. In metabolomics platforms, sensitivity primarily depends on instrumental

choices, such as the chromatographic column type, the mass detector employed, and the application of compound derivatization23. Targeted proteomic approaches sample many data points per

protein, leading to higher accuracy when compared to untargeted methods24. In nuclear magnetic resonance (NMR), no separation takes place and a low number of nuclei change energy status,

leading the detection of only abundant metabolites and lower sensitivity than liquid chromatography (LC)–MS or gas chromatography (GC)–MS. NMR is capable of detecting ~50–75 compounds in

human biofluid, with a lower sensitivity limit of 5 µmolar (ref. 25), while MS platforms are able to measure hundreds to thousands of metabolites in a single sample. Sensitivity in

sequencing platforms depends on the number of reads associated with the feature, a parameter influenced by sequencing depth. Features with an elevated number of reads are more accurately

measured, and hence smaller relative changes can be detected. For region-based omics, where the goal is to identify genomic regions where a certain event occurs, the above definition is

difficult to apply, and sensitivity is described in terms of true positive rate or recall, i.e., the proportion of true sites or regions identified as such, given the number of reads in the

seq output. Reproducibility measures how well a repeated experiment provides the same level for a specific feature or, when referring to technical replicates, the magnitude of dispersion of

measured values for a given true signal. Traditionally, the relative standard deviation (RSD) is used as a measure of reproducibility, with RSD normally differing over the concentration

range in high-throughput platforms26,27. Generally, reproducibility in sequencing platforms improves at high signal levels, such as highly expressed genes or frequent chromatin-related

events. RSD is roughly constant in relation to signal in MS platforms, although in LC–MS the lifetime of the chromatographic column strongly influences reproducibility, leading to small

datasets being more reproducible than experiments with many samples. This constraint imposes the utilization of internal standards, quality control samples, and retention time alignment

algorithms in these technologies28. Moreover, untargeted LC–MS proteomics quantifies protein levels with multiple and randomly detected peptides, each with a different ER, a factor that

compromises the reproducibility of this technique. On the contrary, NMR is a highly linear and reproducible technique29, and reproducibility issues are associated with slight differences in

sample preparation procedures among laboratories. Sequencing methods normally achieve high reproducibility for technical replicates5 and are further improved as sequencing depth increases.

Reproducibility at the library preparation level depends on how reproducible the involved biochemical reactions are. Critical factors affecting reproducibility include RNA stability and

purification protocols in RNA-seq30, antibody affinity in ChIP-seq6, quenching efficiency in metabolomics31, and proteolytic digestion and on-line separation of peptides in proteomics32,33.

Methyl-seq experiments based on the robust _MspI_ enzymatic digestion and bisulfite conversion usually are more reproducible data than enrichment-based methods, such as methylated DNA

immunoprecipitation (MeDIP)34. Finally, reproducibility for DNA variant calling is associated with the balance between read coverage at each genome position and the technology sequencing

errors. The limit of detection (LOD) of a given platform is the lowest detectable true signal level for a specific feature, while the limit of quantitation (LOQ) represents the minimum

measurement value considered reliable by predefined standards of accuracy35. Both limits affect the final number of detected and quantified features, which in turn impacts the number of

tested features and the significance level when correcting for multiple testing. For MS-based methods, LOD and LOQ depend on the platform, can be very different for each compound, and

normally require changes of instrument or sample preparation protocol for different chemicals. Additionally, sample complexity strongly affects LOD, as this reduces the chance of detecting

low-abundance peptides, while pre-fractionation can reduce this effect at the cost of longer MS analysis time. NMR has usually higher LOD than MS-based methods. Conversely, LOD depends

fundamentally on sequencing depth in seq-based technologies, where more features are easily detected by simply increasing the number of reads. However, there also exist differences in LOD

across features in sequencing assays. Shorter transcripts and regions usually have higher LODs and are more affected by sequencing depth choices. For DNA-seq, the ability to detect a genomic

variant is strongly dependent on the read coverage. MS-based and seq-based methods also differ in the way features under LOD are typically treated. MS methods either apply imputation to

estimate values below the LOD (considered missing values)12, or exclude features when repeatedly falling under the LOD. In sequencing methods, LOD is assumed to be zero and data do not

contain missing values, although, also in this case, features with few counts in many samples risk exclusion from downstream analyses. The dynamic range of an omic feature indicates the

interval of true signal levels that can be measured by the platform, while the linear range represents the interval of true signal levels with a linear relationship between the measured

signal value and the true signal value (Fig. 1). These FoM influence the reliability of the quantification value and, consequently, the differential analysis, as detection of the true effect

size depends on the width of these ranges. In proteomics, molecule fragmentation by data-independent acquisition approaches increases the dynamic range by at least two orders of magnitude.

A typical proteomic sample covers protein abundance over 3–4 to four orders of magnitude, a value that increases for targeted approaches36,37. In metabolomics, linear ranges usually span 3–4

orders of magnitude, while dynamic ranges increase to 4–5 orders and can be extended using the isotopic peak of the analytes. A combination of analytical methods can increase the dynamic

range, as different instruments may better capture either high or low concentration metabolites. NMR has a high dynamic range and can measure highly abundant metabolites with precision,

although it is constrained by a high detection limit. For feature-based sequencing platforms, the dynamic range strongly depends on sequencing depth, and values can range from zero counts to

up to hundreds of thousands, or even millions (in RNA-seq, for some mitochondrial RNA transcripts). However, due to technical biases, linear range boundaries are difficult to establish and

may require the use of calibration RNAs (spike-ins). Moreover, linear ranges may be feature dependent and affected by sequence GC content, which then requires specific normalization. For

region-based sequencing platforms, linear and dynamic ranges coincide, and vary from zero to one. A platform displays good selectivity if the analysis of a feature is not disturbed by the

presence of other features. Selectivity influences the number and quantification of features and, consequently, statistical power. For MS platforms, targeted rather than untargeted methods

obtain the best selectivity. In metabolomics, selected reaction monitoring, a procedure that couples two sequential MS reactions to obtain unique compound fragments and control quantitation

bias using isobaric compounds38, is used to improve selectivity, while in proteomics selectivity strongly depends on sample complexity, which determines whether a given feature is detected

or not. Similarly, in sequencing experiments, selectivity relates to competition of fragments to undergo sequencing. Highly abundant features or regions (e.g., a highly expressed transcript

or a highly accessible chromatin region) may outcompete low-abundant elements. Generally, this problem is difficult to address by means other than increasing the sequencing depth. In the

case of transcriptomics, the application of normalized libraries can partially alleviate selectivity problems; however, at the cost of compromising expression level estimations. Particularly

for DNA-seq, variant detection is compromised at repetitive regions and can be alleviated with strategies that increase read length. Identification refers to the relative difficulty faced

when determining the identity of the measured feature, a critical issue in proteomics and metabolomics. In principle, identification does not affect power calculations, but influences

downstream integration and interpretation. Metabolite identification in untargeted MS-based methods requires comparisons with databases that collect spectra from known compounds39,40,41.

Compound fragments with similar masses and chemical properties often compromise identification, while database incompleteness also contributes to identification failures. A typical

identification issue in lipidomics is that many compounds are reported with the same identification label (i.e., sphingomyelins), but slightly different carbon composition and unclear

biological significance. Conversely, NMR is highly specific. Each metabolite has a unique pattern in the NMR spectrum, which is also often used for identification of unknown compounds. For

untargeted proteomics data, either spectral or sequence databases are used to determine the sequence of the measured peptide. Current identification rates lie at ~40–65% of all acquired

spectra with a false discovery rate (FDR) of 1–5%. In targeted approaches, identification is greatly improved by the utilization of isotopically labeled standards. Proteomics suffers from

the additional complexity of combining peptides to identify proteins, which is not straightforward. In fact, a recent study highlighted identification as one of the major problems in

MS-based proteomics due to differences in search engines and databases42 and to high false-positive rates43. A common identification problem in seq-based methods is the difficulty to

allocate reads with sequencing errors or multiple mapping positions, which is addressed either by discarding multi-mapped reads or by estimating correct assignments using advanced

statistical tools44,45. In ChIP-seq, an identification-related issue is the specificity of the antibody targeting the protein or epigenetic modification. Low antibody specificity may result

in reads mapping to nonspecific DNA sequences, leaving true binding regions unidentified. The ENCODE consortium has developed working standards to validate antibodies for different types of

ChIP assays6. The coverage of a platform is defined here as the proportion of detected features in the space defined by the type of biomolecule (aka feature space). Targeted MS platforms

measure a small subset of compounds with high accuracy; hence the coverage is restricted and lower than for untargeted approaches. As sample complexity is frequently much larger than the

sampling capacity of current instruments, even in untargeted methods, identification is limited to compounds with the highest abundances. Repeating sample measurement excluding the features

identified in the first run is an efficient strategy to improve coverage, although this requires increased instrument runtime and sample amounts. Coverage in seq-based methods strongly

depends on sequencing depth and can potentially reach the complete feature space associated with each library preparation protocol. In RNA-seq, oligodT-based methods recover polyA RNAs,

whereas total RNA requires ribo-depletion, capture of antisense transcripts imposes strand-specific protocols, and microRNAs require specific small RNA protocols. In Methyl-seq, coverage

also relates to the applied protocol. Whole-genome bisulfite sequencing has greater genome-wide coverage of CpGs when compared to Reduced Representation by Bisulfite Sequencing (RRBS), while

RRBS and MeDIP provide greater coverage at CpG islands. In general, region-based sequencing approaches can cover the whole reference genome, with coverage depending on the efficiency of the

protocol employed to enrich the targeted regions. FROM FOM TO EXPERIMENTAL DESIGN The FoM analysis across omics revealed that each omic data type possesses different critical performance

metrics. In MS, FoM mainly depend on the choice of instrument and approach—targeted vs. untargeted—, while FoM in sequencing methods rely on sequencing depth, library preparation, and

eventual bioinformatics post-processing. Although FoM are not a property of data but of the analytical platform, they directly impact data characteristics relevant to experimental design.

Overall, FoM strongly relate to the variability in the measurements, which changes in a feature-dependent manner. FoM also determine the final number of measured features and the magnitude

of detectable change. Hence, reproducibility influences measurement variability; sensitivity, linear, and dynamic range determine the magnitude and precision of the measurements, and are

associated to effect size; the number of features measured by the omic platform is given by the LOD, selectivity, identification, and coverage. These three parameters, variability, effect

size, and number of variables, are the key components of power calculations in high-throughput data used by MultiPower to estimate sample size in multi-omic experiments. Figure 3a

illustrates the relationship between platform properties, FoM, power parameters, and MultiPower, while Fig. 3b presents an overview of the MultiPower algorithm (see “Methods” section for

details). MULTIPOWER ESTIMATES SAMPLE SIZE FOR A VARIETY OF EXPERIMENTAL DESIGNS We applied MultiPower to the STATegra data46 (Supplementary Note 1) to illustrate power assessment of an

existing multi-omic dataset. Figure 4 compares the number of features (_m_), expected percentage of features with a significant signal change (_p_1), and variability measured as pooled

standard deviation (PSD). Note that the number of features measured by each omic platform varies by several orders of magnitude, from 60 metabolites to 52,788 DNase-seq regions (Fig. 4a).

This, together with the expected percentage of differentially abundant features (Fig. 4b), affects statistical power when multiple testing correction is applied. Given that PSD is different

for each feature (Fig. 4c), users can set the percentile of PSD for power estimations (see “Methods” section). In this example, PSD equals the third quartile, which is a conservative choice.

We used MultiPower to calculate the optimal number of replicates for each omic imposing a minimum power of 0.6 per technology, an average power of at least 0.8, an FDR of 0.05, an initial

Cohen’s _d_ of 0.8, and same sample size across platforms. MultiPower estimated the optimal number of replicates to be 16 (Fig. 4d, Table 1), which is the number of replicates required by

DNase-seq to reach the indicated minimum power. Power estimates were lowest for DNase-seq, followed by proteomics and miRNA-seq, while features with variability below the _P_60 percentile,

DNase-seq, proteomics, and miRNA-seq displayed power values above 0.8 (Fig. 4e). The power plots also indicated that metabolomics and RNA-seq data had the highest power, implying that  the 

detection of differentially expressed (DE) features for these omics is expected to be easier. As costs for generating 16 replicates per omic might be prohibitive, alternatives can be

envisioned such as allowing a different number of replicates per omic—at the expense of sacrificing power in some technologies—, accepting a higher FDR, or detecting larger effect sizes. For

instance, with four replicates per condition and omic, significant changes were detected at a Cohen’s _d_ of 1.98 (Fig. 4f). Figure 4g depicts a per omic summary of the effective power at

the optimal sample size (_n_ = 16) with a Cohen’s _d_ of 0.8, and at a sample size (_n_ = 4) with a larger Cohen’s _d_. Results showed that a reduction in the number of replicates can

counteract the loss of power if accepting an increase in the magnitude of change to be detected. Finally, MultiPower estimates were further validated by calculating power and Cohen’s _d_

with the published replicate numbers in STATegra (_n_ = 3), and verifying the agreement in magnitude and direction of change between RNA-seq and RT-PCR for six B-cell differentiation marker

genes46 (Supplementary Fig. 1). Experimental designs with different sample sizes per omic may limit statistical analysis options, but might be unavoidable or preferred in certain studies. We

assessed this possibility with the STATegra dataset assuming the same cost for each technology and keeping the rest of the parameters identical to the previous example. MultiPower analysis

revealed that miRNA-seq and DNase-seq required the highest sample size (_n_ = 17), while only six and nine replicates per group were required by metabolomics and RNA-seq, respectively

(Supplementary Table 2, Supplementary Fig. 2). Power plots revealed that decreasing the sample size for miRNA-seq, DNase-seq, or proteomics results in a strong reduction in power. Again, an

alternative to reducing power is to increase the magnitude of change to detect that was initially set to Cohen’s _d_ = 0.8 (Supplementary Fig. 2c). For example, for a sample size not higher

than _n_ = 5, the graph indicates a Cohen’s _d_ of 1.59 for all omics. Additionally, MultiPower can also handle different costs per omic platform and use this information to propose larger

sample sizes for inexpensive technologies (Supplementary Tables 3 and 4, Supplementary Fig. 3). Human multi-omic cohort studies such as The Cancer Genome Atlas database (TCGA) usually

collect data from a large number of subjects, where biological variability is naturally higher than in controlled experiments. In such studies, not all subjects may have measurements at all

omic platforms and when integrating data decisions should be made to either select individuals profiled by all omic assays—to keep a complete multi-omic design—or to allow a different number

of individuals per platform. We illustrate the utility of our method in cohort studies by using MultiPower to estimate power for the integrative analysis of four omic platforms available

for the TCGA Glioblastoma dataset47 (Supplementary Note 1). MultiPower indicated that _n_ = 24 (Supplementary Table 5, Supplementary Fig. 4) is the optimal sample size for complete designs.

In this case, Methyl-seq set the required sample size due to the high number of features, low expected percentage of DE features and high variability of this dataset. As the optimal sample

size is similar to the number of samples available in the less prevalent omics modality (only 22 samples are available for proneural tumor in methylation data), the joint analysis of current

data is not expected to suffer from a major lack of power (Supplementary Fig. 5). However, smaller sample sizes would dramatically impact the number of detected DE features (Supplementary

Fig. 5), further validating the results of the MultiPower method. Given that power is affected by the number of omic features (Fig. 3a), an alternative to adjusting power here is the

exclusion of methylation features with low between-group variance, as this reduces the magnitude of the multiple testing correction effect on the loss of power. MultiPower helps to assess

these options. For example, keeping only methylation sites with an absolute log2 fold change >0.05 for the power analysis resulted in a reduction of the optimal sample size from 24 to 22

(Supplementary Table 6). MULTIML PREDICTS SAMPLE SIZE FOR MULTI-OMIC BASED PREDICTORS Multi-omics datasets may be used in cohort studies to classify biological samples into, for instance,

disease subtypes or to predict drug response. In these cases, the analysis goal is not to detect a size effect but to achieve a specified prediction accuracy. MultiML computes the optimal

sample size for this type of problem. Briefly, MultiML uses a pilot multi-omics dataset to estimate the relationship between sample size and prediction error, which is then used to infer the

sample size required to reach a target classification ER (Fig. 5a, “Methods” section). MultiML is a flexible framework that (i) predicts sample sizes using different combinations of omics

platforms to obtain the best predictive set, as omics technologies may have similar or complementary information content for a given classification scenario; (ii) accepts user-provided

machine learning algorithms beyond the implemented partial least squares discriminant analysis (PLS-DA) and random forest (RF) methods; and (iii) offers job parallelization options to speed

up calculations when high-performance computing resources are available. We illustrate MultiML performance using TCGA Glioblastoma data47. Omic features were used to predict tumor subtypes

with RF, and the target classification error rate (ERtarget) was set to 0.01. Sample sizes were calculated for combinations of two to five omics platforms. We found that the number of

samples required to obtain ERtarget decreased as the number of omics data platforms increased, suggesting that complementary information was captured by the multi-omics approach resulting in

a more efficient predictor (Fig. 5b). Figure 5c shows the classification ER curve fitted by MultiML for a predictor with four omics. A quadratic pattern is observed, where ERs rapidly

decrease as the number of samples increases to reach a stable classification performance. This graph can be used to calculate the number of samples required at different ER levels. To

validate the estimations given by MultiML, we mimicked a prediction scenario where we took fractions of the Glioblastoma data and used MultiML to estimate the sample size for ERtarget equal

to the ER of the complete dataset (MinER) or greater. Then, for the predicted sample sizes, we obtained their actual ER from the data and compared them to ERtarget to evaluate the accuracy

of the MultiML estimate, and if the magnitude of the input dataset affected this accuracy. As expected, MultiML accuracy increased with the size of the input data and the number of included

omics types (Fig. 5d). Accurate predictions (deviations < 5%) were obtained with 50 samples in a three omics combination. Results were similar for other values of ERtarget (Supplementary

Fig. 6). We concluded that the sample size could be accurately predicted when input data represents ~40–60% of the required sample size. DISCUSSION As multi-omic studies become more common,

guidelines have been proposed for dealing with experimental issues (i.e., sample management) associated with specific omics data types48. However, the field has yet to address aspects that

are essential to understand the complexity of multi-omic analysis, such as the definition of performance parameters across omic technologies and the formulation of an experimental design

strategy in multi-omic data scenarios. In this study, we addressed both issues by proposing FoM as a language to compare omic platforms, and by providing algorithms to estimate sample sizes

in multi-omic experiments aiming at differential features analysis (MultiPower) or at sample classification using ML (MultiML). FoM have traditionally been used in analytical chemistry to

describe the performance of instruments and methods. These terms can also be intuitively applied to sequencing platforms, but we noticed that the meaning and relevance of FoM slightly differ

for both types of technologies. Here, we explain FoM definitions across omic platforms and discuss which of these metrics are critical to each data type. Detection limit, selectivity,

coverage, and identification are FoM with critical influence on the number of features comprising the omics dataset, which in turn affects the power of the technology to identify features

with true signal changes. Power diminishes as the number of features increases due to the application of multiple testing corrections to control false positives. Reproducibility and dynamic

range may also be very different across platforms, and these have a direct impact on the within-condition variability and across-condition differences of the study. Moreover, while

sequencing depth critically affects many of the described FoM of sequencing platforms, in MS-based methods, the choice of a targeted or untargeted method strongly influences FoM values. The

number of features detected by the omic platform together with the different measurement variabilities across features and the magnitude of change to be detected, represent major components

of power calculations for omics data. The highly heterogeneous nature of these factors across omics platforms calls for specific methods for power calculations in multi-omic experiments,

which is addressed by MultiPower. MultiPower solves the optimization problem of obtaining the sample size that minimizes the cost of the multi-omic experiment, while ensuring both a required

power per omic and a global power. As any power computation approach, MultiPower indicates the sample size required to detect a targeted effect size given a significance threshold.

MultiPower graphically represents the relationship between sample size, dispersion, and statistical power of each omic, and facilitates exploration of alternative experimental design

choices. Estimates for MultiPower parameters are optimally calculated from pilot data, although they can also be manually provided. The tool accepts normally distributed, count and binary

data to facilitate the integration of omic technologies of different analytical nature. Data should have been properly preprocessed and eventual batch effects, removed. In this study, we

showcase MultiPower functionalities using sequencing, microarray, and MS data, although the method could be applied to other technologies, such as NMR. Importantly, the optimal sample size

can be computed under two different requirements: an equal sample size for all platforms ensuring a common minimal power, or different sample size per omic to achieve the same power. This is

relevant for the choice of downstream statistical analysis. Methods that rely on co-variance analysis typically require uniform sample sizes and MultiPower will provide this while revealing

the differences in power across data modalities. Methods that combine data based on effect estimates allow sample size differences and can benefit from the equally powered effect

estimation. We illustrate the MultiPower method in three scenarios, where different parameterizations are assessed and include both controlled laboratory experiments and cohort data to

highlight the general applicability of the method. By discussing interpretations of power plots and the factors that contribute to sample size results, we provide a means to make informed

decisions on experimental design and to control the quality of their integrative analysis. The MultiPower approach is not directly applicable to ML methods used for sample classification, as

in this case the basic parameters of the power calculation—significance threshold and effect size—are not applicable. Still, sample size estimation is relevant as multi-omic approaches are

frequently used to build classifiers of biological samples. This is not a trivial problem because, aside from FoM, feature relationships within the multivariate space are instrumental in ML

algorithms. The MultiML strategy calculates samples size for multi-omic applications, where the classification ER can be used as a measure of performance. MultiML is itself a learning

algorithm that learns the relationship between sample size and classification error, and uses this to estimate the number of observations required to achieve the desired classification

performance. Hence, pilot data are a requisite for MultiML. Additionally, MultiML has been designed to be flexible for the ML algorithm and to evaluate multiple combinations of omics types

in order to identify optimized multi-omic predictors. Altogether this work establishes, for the first time, a uniform description of performance parameters across omic technologies, and

offers computational tools to calculate power and sample size for the diversity of multi-omics applications. We anticipate MultiPower and MultiML will be useful resources to boost powered

multi-omic studies by the genomics community. METHODS SCOPE OF THE FOM ANALYSIS In this study, we discuss seven FoM, which we broadly classified into two groups: quantitative or analytical

FoM include sensitivity, reproducibility, detection and quantification limit, and linear or dynamic range, and qualitative FoM, which are selectivity, identification, and coverage. To

describe how they apply to omic technologies, we distinguish between MS and seq-based platforms. MS platforms refer to metabolomics and proteomics, which often operate in combination with

LC–MS or GC–MS. MS platforms can be used for “untargeted” (measuring a large number of features including novel compounds) and “targeted” assays. While MS is the platform used in most

proteomics and metabolomics based studies, NMR (refs. 29,49) is also a relevant platform in metabolomics and is incidentally discussed. For sequencing platforms, we also consider two

subgroups: “feature-based” and “region-based”. In feature-based assays (i.e., RNA-seq or miRNA-seq), a genome annotation file defines the target features to be quantified, and hence these

are known a priori. For region-based assays (i.e., ChIP-seq or ATAC-seq), the definition of the target feature to be measured (usually genomics regions) is part of the data analysis process.

Applications of RNA-seq to annotate genomes could be considered a region-based assay. We consider here omic assays with a dynamic component regarding the genotype, such as RNA-seq,

ChIP-seq, ATAC-seq, Methyl-seq, proteomics, and metabolomics, and also genome variation analyses. However, single-cell technologies are not included, as they require a separate discussion.

Analytical FoM quantify the quality of an analytical measurement platform and are defined at the feature level (gene, metabolite, region, etc.). We describe FoM as properties of a

calibration line that displays the relationship between the measured value and the true quantity of the feature in the sample (Fig. 1). In our case, the definition of the true signal differs

between omic platforms. As MS platforms and feature-based seq-based platforms measure the concentration or level of the feature of the gene, protein, or metabolite of interest, the true

signal represents the average level across all cells contained in the sample (Fig. 1a). In contrast, region-based sequencing techniques aim to identify the genomic region, where a given

molecular event occurs, such as the binding of a transcription factor. In this case, the true signal represents the fraction of cells in the sample (or probability), where the event actually

occurs within the given coordinates (Fig. 1b). Lastly, while analytical FoM are defined at the feature level, omic platforms by nature measure many features simultaneously and consequently,

the FoM may not be uniform for all of them. For example, accuracy might be different for low vs. highly expressed genes or polar vs. apolar metabolites. In this study, we consider FoM

globally and discuss how technological or experimental factors affect the FoM of different ranges of features within the same platform. OVERVIEW OF MULTIPOWER METHOD The MultiPower R method

(Fig. 3b) performs a joint power study that minimizes the cost of a multi-omics experiment, while requiring both a minimum power for each omic and an average power for all omics. MultiPower

calculations are defined for a two groups contrast and implemented in the R package to support the application of the method to single and multiple pairwise comparisons. The parameters

required to compute power can be estimated from multi-omic available data (pilot data or data from previous studies) or, alternatively, users can set them. The method considers multiple

testing corrections by adjusting the significance level to achieve the indicated FDR. Additionally, MultiPower accepts normally distributed data, count data or binary data, and optimal

sample size (number of replicates or observations per condition) can be computed either requiring the same or allowing different sample sizes for each omic. In the latter, the monetary cost

is considered as an additional parameter in the power maximization problem. MultiPower can be used to both design a new multi-omic experiment and to assess if an already generated multi-omic

dataset provides enough power for statistical analysis. MultiPower minimizes the total cost of the multi-omics experiment while ensuring a minimum power per omic (_P__i_) and a minimum

average power for the whole experiment (_A_). Equation (1) describes the optimization problem to be solved to estimate the optimal number of biological replicates for each omic (_x__i_):

$$\begin{array}{l}{\mathrm{min}}\mathop {\sum}\limits_{i = 1}^I {2c_ix_i} \\ {\mathrm{subject}}\,{\mathrm{to}}\!\!:\\ f\left( {x_i,\alpha , \ldots } \right) \ge P_i \quad\forall i = 1,

\ldots ,I\\ \frac{{\mathop {\sum }\nolimits_{i = 1}^I f\left( {x_i,\, \alpha , \ldots } \right)}}{I} \ge A\\ x_i \in {\Bbb Z}^ + \end{array}$$ (1) Where _I_ is the number of omics, _c__i_ is

the cost of generating a replicate for omic _i_, _α_ is the significance level, and _f_() represents the power function. We calculate statistical power under the assumption that the means

of two populations are to be compared in the case of count or normally distributed data. Consequently, power is in these cases a function of the sample size (_x__i_) per condition and for a

particular omic _i_, the significance level (_α_), and other parameters that depend on the nature of the omic data type. For normally distributed data, a _t_-test is applied and the power

for omic _i_ is expressed as \(f\left( {x_i,\alpha ,\Delta _i,\sigma _i} \right)\), where Δ_i_ is the true difference of means in absolute value to be detected, and _σ__i_ is the PSD

considering two experimental groups. Count data obtained from sequencing platforms can be modeled as a negative binomial distribution (NB) and an exact test can be applied to perform

differential analysis. In this case, the power of omics _i_ is estimated as described in ref. 50, where power is expressed as \(f\left( {x_i,\alpha ,\phi _i,\mu _i,\omega _i} \right)\),

being _ϕ__i_ the dispersion parameter of the NB that relates variance and mean (see Eq. (2)). The effect size is calculated with the fold change (_ω__i_) between both groups as well as the

average counts (_μ__i_). $$\sigma ^2 = \mu + \mu ^2\phi$$ (2) For binary data with 0/1 or TRUE/FALSE values indicating, for instance, if a mutation is present or not, or if a transcription

factor is bound or not, the goal is comparing the percentages of 1 or TRUE values between two populations. In this case, the parameters needed to estimate power are related to the difference

between proportions to be detected (the effect size) and the sample size, but variability is not considered. As MultiPower considers multiple testing correction to control FDR, the

significance level given to the power function is adapted to this correction (_α*_). We followed the strategy proposed in other studies51,52,53 given by Eq. (3). $$\alpha ^ \ast =

\frac{{r_1\alpha }}{{(m - m_1)(1 - \alpha )}},$$ (3) where _m_ is the number of features in a particular omic, _m__1_ is the number of expected DE features, _r__1_ is the expected number of

true detections, and _α_ is the desired FDR. SAMPLE SIZE SCENARIOS IN MULTIPOWER In multi-omic studies, an assorted range of experimental designs can be found. All omic assays may be

obtained on the same biological samples or individuals, which would result in identical replicates number for all data types. However, this is not always possible due to restrictions in cost

or biological material, exclusion of low-quality samples, or distributed omic data generation. In these cases, sample size differs among omic types and yet the data are to be analyzed in an

integrative fashion. MultiPower contemplates these two scenarios. Under the first scenario, adding the constraint of equal sample size for all omics (_x__i_ = _x_ for all _I_ = 1, …, _I_)

to the optimization problem in Eq. (1) results in a straightforward solution. First, the minimum sample size required to meet the constraint on the minimum power per omic (_x__i_) is

calculated and the initial estimation of _x_ is set to _x_ = maxI{_x__i_}. Next, the second constraint on the average power is evaluated for _x_. If true, the optimal sample size is _x_opt =

 _x_. Otherwise, _x_ is increased until the constraint is met. Note that, under this sample size scenario, the cost per replicate does not influence the optimal solution _x_opt. Under the

second scenario, allowing different sample sizes for each omic, the optimization problem in Eq. (1) becomes a nonlinear integer programming problem, as the statistical power is a nonlinear

function of _x__i_. The optimization problem can be transformed into a 0–1 linear integer programming problem by defining the auxiliary variables \(z_n^i\) for each omic _i_ and each

possible sample size _n_ from 2 to a fixed maximum value _n__i_max, where \(z_n^i = 1\) when the sample size for omic _i_ is _n_. The new linear integer programming problem can be formulated

as follows: $$\begin{array}{l}{\mathrm{min}}\mathop {\sum}\limits_{i = 1}^I {2c_i} \left( {\mathop {\sum }\limits_{n = 2}^{n_{\mathrm{max}}^i} nz_n^i} \right)\\

{\mathrm{subject}}\,{\mathrm{to}}\!\!:\\ \mathop {\sum}\limits_{n = 2}^{n_{\mathrm{max}}^i} {f_i} \left( n \right)z_n^i \ge P_i \, \, \forall i = 1, \ldots ,I\\ \frac{{\mathop {\sum

}\nolimits_{i = 1}^I \mathop {\sum }\nolimits_{n = 2}^{n_{\mathrm{max}}^i} f_i(n)z_n^i}}{I} \ge A\\ \mathop {\sum}\limits_{n = 2}^{n_{\mathrm{max}}^i} {z_n^i} = 1{\quad}i = 1, \ldots ,I\\

z_n^i\, \in \{ 0,1\}\quad\forall i\,\, \forall n\end{array},$$ (4) where _f__i_(_n_) is the power for sample size _n_, given the parameters of omic _i_. MULTIPOWER IMPLEMENTATION The

MultiPower R package implements the described method together with several functionalities to support both the selection of input parameters required by the method and the subsequent

interpretation of the results. The R package and user’s manual are freely available at https://github.com/ConesaLab/MultiPower. The MultiPower package requires different parameters to

compute the optimal sample size. As the choice of parameters can be challenging, MultiPower can estimate them from pilot or similar existing data. The multi-omic pilot data must have two

groups and at least two replicates per group. The algorithm assumes data are already preprocessed, normalized, and free of technical biases. Both normally distributed and count data are

accepted. We recommend raw count data to be provided for sequencing technologies as MultiPower deals with the sequencing depth bias. However, when count data contains other sources of

technical noise, we recommend previous transformations to meet normality (e.g., with log or voom transformation) and indicating MultiPower that data are normally distributed. We also

recommend removing low count features from sequencing data. For data containing missing values, these must be removed or imputed before running MultiPower. MultiPower also accepts binary

data (e.g., SNP data, ChIP-seq transcription binding data, etc.). In this case, values must be either 0–1 or TRUE/FALSE. Each data type requires a different sample size computation. For

normally distributed data, MultiPower uses the _power.t.test()_ function from _stats_ R package (based on a classical _t_-test), while the _sample_size()_ and _est_power()_ functions from R

Bioconductor _RnaSeqSampleSize_ package54 are used for count data, where a NB test is applied. For binary data, the _power.prop.test()_ function from stats R package is used. Moreover,

MultiPower transforms parameters provided by the user to fit specific arguments required by these functions, in such a way that magnitudes are maintained roughly comparable for all data

types. The power function for normally distributed data depends on the effect size, i.e., the true difference of means to be detected (delta parameter, Δ). The delta parameter depends on the

dynamic range of the omic and may be nonintuitive following data preprocessing. On the contrary, the fold change and mean counts are used in count data to estimate power. Therefore,

MultiPower uses instead the Cohen’s _d_ (_d__0__)_ value to homogenize input parameters. Cohen’s _d_ is defined as Δ/_σ_ and does not depend on the scale of the data as occurs for the Δ

value. Therefore, the same value can be chosen for all omic platforms. Cohen55 and Sawilowsky56 proposed the classification presented in Supplementary Table 7 to establish a Cohen’s _d_

value. MultiPower computes the Cohen’s _d_ value for all omic features and applies this value to estimate the set M1 of DE features (those with _d_ > _d_0), which are called pseudo-DE

features. We recommend setting the same Cohen’s _d_ initial value (_d_0) for all the omics although MultiPower allows different values for each one of them. The equivalent to Cohen’s _d_

when comparing proportions in groups A and B is Cohen’s _h_, which can be defined as _h_ = |φ_A_ _−_ φ_B_|, where φ_i_ = 2 arcsin √_pi_, and _pi_ is the proportion of 1 or TRUE values in

group _i_. Classification in Supplementary Table 7 is also valid for Cohen’s _h_. The multiple testing correction is applied to each omic analysis (see Eq. (3)), taking the significance

level set by the user as FDR value. The user must also provide the expected percentage of DE features (_p_1) for each omic. Given the number of features in a particular omic (_m_), the

expected number of DE features can be simply represented as _m_1 = _mp_1. The RnaSeqSampleSize package50 estimates the expected number of true detections _r_1 for count data. For normal or

binary data, _r_1 = _m_1 is assumed(as in ssize.fdr R/CRAN package57). The intrinsic characteristics of each omic feature may result in different power values for each one of them. To have a

unique power estimation per omic, an average power parameter from the distribution of such parameters across pseudo-DE features must be provided. For normally distributed data, the PSD

parameter (_σ_) is computed as the percentile _P__k_ of the PSDs for all the pseudo-DE features, where _P__k_ is set by the user (default value _P_75). Thus, the Δ estimation should equal

the chosen PSD. However, to avoid dependence on a single value, MultiPower evaluates all the pseudo-DE features with PSD between percentiles _P__k_−5 and _P__k_+5 and the _P_100 − _k_ of the

corresponding Δ values is taken as conservative choice. For count data, MultiPower estimates the parameter _w_ that considers the different sequencing depth between samples as _w_ = 

_D__B__/D__A_, where _D__i_ is the geometric mean of the sequencing depth of the samples in group _i_ divided by median of the sequencing depth of all samples (MSD). To compute the rest of

parameters, count values are normalized by dividing them by this ratio, that is, the sequencing depth of the corresponding sample divided by MSD. To be consistent with the previous choice

for normally distributed data, the variance per condition (_σ_2) is also estimated as the percentile _P__k_ of the variances for all pseudo-DE features and conditions. Mean counts (_μ_) are

obtained as the percentile _P_100−_k_ of mean counts in the reference group (A) corresponding to pseudo-DE features with variance between percentiles _P__k_−5 and _P__k_+5. The dispersion

parameter (_ϕ_) is then derived from Eq. (2). Finally, the fold change of pseudo-DE features (_ω_) is estimated as the percentile _P_100−_k_ of the fold changes corresponding to pseudo-DE

features with a PSD between percentiles _P__k_−5 and _P__k_+5. For binary data, the proportions chosen to estimate power correspond to the _P_100−_k_ of pseudo-DE features for Cohen’s _d_,

and are stored in the delta output parameter of MultiPower. As variability is not considered for this data type, dispersion power plots are not generated in this case. Once the power

parameters are obtained for each omic and the user sets the minimum power per omic and the average power for the experiment, the optimization problem in Eq. (4) is completely defined and

MultiPower makes use of _lpmodeler_ and _Rsymphony_ R packages to solve it. Note that the application of these packages to solve the problem is only needed when the number of replicates for

each omic differs. MultiPower returns a summary table with the provided and/or estimated power parameters, the obtained optimal sample size, and corresponding power per omic. POWER

PARAMETERS IN THE ABSENCE OF PRIOR DATA While parameter estimation from previous data is recommended for MultiPower analysis, this might not always be feasible. In this case, MultiPower

requires parameters to be provided by users, which could be challenging. Here, we provide recommendations for critical MultiPower parameters. The average value for the standard deviation per

omic feature and condition partially depends on the reproducibility of omics technology. Overestimating this parameter guarantees that the sample size fits the power needed but may lead to

too large sample sizes. According to our experience, a good value for the standard deviation is 1. Value for the expected proportion of DE features per omic should be set according to

results seen in similar studies. A high percentage is expected for cell differentiation processes or diseases like cancer, while small perturbations or other types of diseases may induce

fewer changes. Typical values for the minimum fold change between conditions and the mean of counts for the DE features when using count data are 2 and 30, respectively, but again these

values depend on the sequencing depth of the experiment and the magnitude of the expected molecular changes. POWER STUDY After obtaining the optimal sample size with MultiPower, some

questions may still arise, especially when this sample size exceeds the available budget for the experiment: * How much reduction of the sample size can we afford without losing too much

power? * If power cannot be decreased but the sample size has to be reduced, how will this reduction influence the effect size to be detected? * Can we remove any omic platform with

negligible changes between conditions, since this platform imposes a too large optimal sample size? To provide answers to these and similar questions, MultiPower returns several diagnostic

plots (see Fig. 4d–g for instance). The power vs. sample size plot shows variations in power as a function of the sample size. The power vs. dispersion plot also displays the power curves

but for different dispersion values (PSD in normal data or _ϕ_ parameter in count data). In both plots, the power for the estimated optimal sample size or the fixed dispersion value is

represented by a square dot. If the optimal sample size estimated by MultiPower exceeds the available budget, researchers may opt for increasing the effect size (given by the Cohen’s _d_) to

be detected and allowing a smaller sample size without modifying the required power. To perform this analysis, the _postMultiPower()_ function can be applied, which computes the optimal

sample size for different values of Cohen’s _d_, from the initial value set by the user to _d_max = min_i in I_{_P_90_i_(_d_)}, where _P_90_i_(_d_) is the 90th percentile of the Cohen’s _d_

values for all the features in omic _i_. This choice ensures sufficient pseudo-DE features to estimate the rest of the parameters needed to compute power. MULTIPOWER FOR MULTIPLE COMPARISONS

Although MultiPower algorithm is essentially defined for a two groups comparison, the MultiPower R package supports experimental designs with multiple groups. Assuming that a pilot dataset

is available, the _MultiGroupPower()_ function automatically performs all the possible pairwise comparisons (or those comparisons indicated by the user) and returns both a summary of the

power and optimal sample size for each comparison, and a numerical and graphical global summary for all the comparisons. In this global summary, the global optimal sample size is computed as

the maximum of optimal sizes obtained for the individual comparisons. Therefore, the solution given by MultiPower method does not allow a different sample size for each group. Users must be

aware that different optimal sample size could be obtained in this case. MULTIML METHOD The MultiML method deals with a multi-omic sample size estimation problem, in which we have prior

data consisting of a list of _O_ omic data matrices of dimension _N_ observations × _P_ predictor variables, and a categorical response variable Y providing the class each observation

belongs to (Fig. 5). The number of observations and variables can differ across omics. MultiML estimates the optimal sample size required to minimize the classification ER. MultiML allows 

users to perform analyses for different combinations of the _O_ available omics. In each combination, the algorithm selects the common observations across omics, _N_max. Next, an increasing

number of observations (from two observations per class to the total number of observations _N_max) are selected to build a class predictor using the ML algorithm, sampling strategy (SS),

and cross-validation (CV) method indicated by the user. The algorithm incorporates a LASSO variable selection step to reduce the number of predictors and computation time. LASSO regression

is incorporated at the performance evaluation step to avoid overfitting. This process is repeated 15 times as default, and for each iteration the classification ER of the predictor is

computed. These data are used to build a polynomial model that describes the relationship between ER and the number of observations in the multi-omics dataset, which can be then used to

estimate the sample size required for a given ERtarget. Supplementary Fig. 7 shows the pseudocode of the MultiML algorithm. MULTIML IMPLEMENTATION MultiML is implemented as a set of R

functions that calculate the classification ERs at increasing number of observations, fit the sample size predictive model and graphically display results. Auxiliary functions are included

to prepare multi-omic data and optimize computational requirements. The main function is _ER_calculator()_, which basically takes multi-omic pilot data and returns the estimated sample size.

This function requires an ERtarget, which is the maximum classification ER that the user is willing to accept in the study. When not provided by the user, MultiML takes the ER value

obtained from the pilot data. Users may select from two CV methods, tenfold and leave-one-out CV, and prediction performance results are averaged across iterations. MultiML can operate with

any user-supplied ML algorithm, provided that this is a wrapped R function with input and output formats supported by MultiML. By default, MultiML includes RF and PLS-DA as ML options. For

RF the R package _randomForest_58 is required. In this method, the classification ER is calculated after constraining all selected omics variables into a wide matrix. For PLS-DA the

_mixOmics_ R package59 is required. In this case, each omics data matrix is reduced to its significant variables and analysis is performed maintaining a three-way _N_ × _P_ × _O_ structure,

where _N_ are individuals, _P_ are the significant variables, and _O_ are the different omics in the study. If PLS-DA is selected as ML method, the SSs may or not be balanced, returning

either an overall classification ER or a balanced ER calculated on the left-out samples. For RF method, only ER is available as both methods give similar results. MultiML also provides

different prediction distances for PLS-DA and RF used to assign a category to samples. For PLS-DA, maximum distance, distance to the centroid, and Mahalanobis distance were implemented.

These prediction distances can be defined as a model with _H_ components. Given _N_newInds new individuals and their corresponding omic data matrix XNEWINDS, the predicted response variable

ŶNEWINDS can be computed as follows: $$\widehat {\mathbf{Y}}_{{\mathbf{newinds}}} = {\mathbf{X}}_{{\mathbf{newinds}}} \times {\mathbf{W}}\left( {{\mathbf{D}}^{\mathbf{T}}{\mathbf{W}}}

\right)^{ - {\mathrm{1}}}{\mathbf{B}}$$ (5) where W is a _p_ (variables) × _H_ matrix containing the loading vectors associated with X; D is a _p_ × _H_ matrix containing the regression

coefficients of X on its _H_ latent components; and B is an _H_ × _n_ (individuals) matrix containing the regression coefficients of Y on the _H_ latent components associated to X. The

predicted scores (Tpred) are computed as: $${\mathbf{T}}_{{\mathbf{pred}}} = {\mathbf{X}}_{{\mathbf{newinds}}} \times {\mathbf{W}}\left( {{\mathbf{D}}^{\mathbf{T}}{\mathbf{W}}} \right)^{ -

{\mathbf{1}}}$$ (6) In turn, for RF, out-of-bag (OOB) estimate was included60. The RF classifier is trained using bootstrap aggregation, where each new tree is fit from a bootstrap sample of

the training observations _z__i_ = (_x__i__, y__i_). The OOB error is the average error for each _z__i_ calculated using predictions from the trees that do not contain _z__i_ in their

respective bootstrap sample. The prediction distances are then applied to assign a category to each new sample. To reduce the number of omics variables and computational time, a generalized

linear model via penalized maximum likelihood is applied. The regularization path is computed for the LASSO penalty using the _glmnet_ R package61. This variable selection step is performed

on a random selection of _n_ observations and repeated as many times as required (15 by default) to retain the _q_ variables that best explain the classification vector Y. The algorithm then

takes a new set of _n_′_i_ observations and, uses only the _q_ variables to calculate the classification ER using the ML and CV method chosen by the user (Fig. 5). The sample size

prediction curve is estimated with the vector of ERs \(\overline {{\mathbf{ER}}_{{\mathbf{ti}}}}\) and the vector of number of samples ΤI. The accuracy of MultiML depends on the number of

ticks obtained to fit the sample size prediction curve. The algorithm starts with a low (5) number of ticks and iteratively increases them until the addition of new ticks does not improve

the accuracy of the sample size prediction curve. The algorithm termination protocol implemented in MultiML, forces a stop when at least 12% of the range of values of three consecutive

models (ticks addition steps) are equal. Finally, a first-order-smoothed penalized P-spline calculation is performed to model the relationship between the number of samples and the

classification ER (refs. 62,63). The degrees of freedom of this model are the number of observation subsets evaluated (ticks) minus 1. The model is used to predict the sample size required

to obtain a given classification error. MultiML is a computationally intensive algorithm. The function _RequiredTimeTest()_ allows users to estimate the time required to run the full

predictive model at the local installation. For users who can benefit from parallelization options, we have implemented the _slurm_creator()_ R function that creates a. sh script to run

MultiML calculations in a SLURM cluster. Moreover, MultiMIL can be run incrementally. The function _Previous_CER()_ allows the utilization of a previous MultiML result with _N_ samples in a

new MultiML calculation that expands the size of the prior dataset by _M_ samples, thereby significantly accelerating the calculation of the new model. MULTIML OUTPUT MultiML returns all

numerical data of the ML models created to fit the sample size prediction model. This includes the evaluated subsets of observations and data types, the classification ER values obtained at

each iteration, and the predicted sample size together with the margin of error of the prediction. Additionally, the function _ErrorRatePlot()_ prints graphically the relationship between

different sample sizes and their corresponding classification ERs. An example is shown in Fig. 5c. The plot also includes the fitted penalized smooth spline model to graphically obtain the

sample size for an ERtarget not achievable with the pilot dataset. The user can also create a comparative plot of all omic combinations to determine the best contributing data modality to an

accurate classification by using _Comparative_ERPlot()_ function. REPORTING SUMMARY Further information on research design is available in the Nature Research Reporting Summary linked to

this article. DATA AVAILABILITY The STATegra data used in this manuscript are available from: Gene Expression Omnibus with accession numbers GSE75417, GSE38200, GSE75394, GSE75393, and

GSE75390; https://identifiers.org/pride.project:PXD003263; and https://identifiers.org/metabolights:MTBLS283. The TCGA glioblastoma data used in this manuscript are available from

https://www.cancer.gov/about-nci/organization/ccg/research/structural-genomics/tcga/studied-cancers/glioblastoma. CODE AVAILABILITY The MultiPower and MultiML methods are available at GitHub

repository https://github.com/ConesaLab/MultiPower. REFERENCES * Thingholm, L. B. et al. Strategies for integrated analysis of genetic, epigenetic, and gene expression variation in cancer:

addressing the challenges. _Front. Genet._ 7, 2 (2016). Article  PubMed  PubMed Central  CAS  Google Scholar  * Blatti, C., Kazemian, M., Wolfe, S., Brodsky, M. & Sinha, S. Integrating

motif, DNA accessibility and gene expression data to build regulatory maps in an organism. _Nucleic Acids Res._ 43, 3998–4012 (2015). Article  CAS  PubMed  PubMed Central  Google Scholar  *

Fagan, A., Culhane, A. C. & Higgins, D. G. A multivariate analysis approach to the integration of proteomic and gene expression data. _Proteomics_ 7, 2162–2171 (2007). Article  CAS 

PubMed  Google Scholar  * Conesa, A., Prats-Montalbán, J. M., Tarazona, S., Nueda, M. J. & Ferrer, A. A multiway approach to data integration in systems biology based on Tucker3 and

N-PLS. _Chemometrics Intell. Lab. Syst._ 104, 101–111 (2010). Article  CAS  Google Scholar  * Conesa, A. et al. A survey of best practices for RNA-seq data analysis. _Genome Biol._ 17, 13

(2016). Article  PubMed  PubMed Central  CAS  Google Scholar  * Landt, S. G. et al. ChIP-seq guidelines and practices of the ENCODE and modENCODE consortia. _Genome Res._ 22, 1813–1831

(2012). Article  CAS  PubMed  PubMed Central  Google Scholar  * Wei, Z., Zhang, W., Fang, H., Li, Y. & Wang, X. esATAC: an easy-to-use systematic pipeline for ATAC-seq data analysis.

_Bioinformatics_ 34, 2664–2665 (2018). Article  CAS  PubMed  PubMed Central  Google Scholar  * Sun, Z. et al. SAAP-RRBS: streamlined analysis and annotation pipeline for reduced

representation bisulfite sequencing. _Bioinformatics_ 28, 2180–2181 (2012). Article  CAS  PubMed  PubMed Central  Google Scholar  * Xia, J. & Wishart, D. S. Using MetaboAnalyst 3.0 for

comprehensive metabolomics data analysis. _Curr. Protoc. Bioinformatics_ 55, 14.10.1:14.10.91 (2016). * Davidson, R. L., Weber, R. J. M., Liu, H., Sharma-Oates, A. & Viant, M. R.

Galaxy-M: a Galaxy workflow for processing and analyzing direct infusion and liquid chromatography mass spectrometry-based metabolomics data. _Gigascience_ 5, 10 (2016). Article  PubMed 

PubMed Central  CAS  Google Scholar  * Goeminne, L. J. E., Gevaert, K. & Clement, L. Experimental design and data-analysis in label-free quantitative LC/MS proteomics: a tutorial with

MSqRob. _J. Proteom._ 171, 23–36 (2018). Article  CAS  Google Scholar  * Codrea, M. C. & Nahnsen, S. Platforms and pipelines for proteomics data analysis and management. _Adv. Exp. Med

Biol._ 919, 203–215 (2016). Article  CAS  PubMed  Google Scholar  * Park, Y., Figueroa, M., Rozek, L. & Sartor, M. MethylSig: a whole genome DNA methylation analysis pipeline.

_Bioinformatics_ 30, 2414–2422 (2014). Article  CAS  PubMed  PubMed Central  Google Scholar  * Andrews S. FASTQC. _A Quality Control Tool for High Throughput Sequence Data_.

http://www.bioinformatics.babraham.ac.uk/projects/fastqc/ (2014). * García-Alcalde, F. et al. Qualimap: evaluating next-generation sequencing alignment data. _Bioinformatics_ 28, 2678–2679

(2012). Article  PubMed  CAS  Google Scholar  * Okonechnikov, K., Conesa, A. & Garcia-Alcalde, F. Qualimap 2: advanced multi-sample quality control for high-throughput sequencing data.

_Bioinformatics_ 32, 292–294 (2016). CAS  PubMed  Google Scholar  * Lassmann, T., Hayashizaki, Y. & Daub, C. O. SAMStat: monitoring biases in next generation sequencing data.

_Bioinformatics_ 27, 130–131 (2011). Article  CAS  PubMed  Google Scholar  * Ewels, P., Magnusson, M., Lundin, S. & Käller, M. MultiQC: summarize analysis results for multiple tools and

samples in a single report. _Bioinformatics_ 32, 3047–3048 (2016). Article  CAS  PubMed  PubMed Central  Google Scholar  * Poplawski, A. & Binder, H. Feasibility of sample size

calculation for RNA-seq studies. _Brief. Bioinform._ 19, 713–720 (2018). CAS  PubMed  Google Scholar  * Li, C.-I., Samuels, D. C., Zhao, Y.-Y., Shyr, Y. & Guo, Y. Power and sample size

calculations for high-throughput sequencing-based experiments. _Brief. Bioinform._ 19, 1247–1255 (2018). Article  CAS  PubMed  Google Scholar  * Banko, M. & Brill, E. Scaling to very

very large corpora for natural language disambiguation. In _Proceedings of the 39th Annual Meeting of the Association for Computational Linguistics_ 26–33 (Association for Computational

Linguistics, France, 2001). * Figueroa, R. L., Zeng-Treitler, Q., Kandula, S. & Ngo, L. H. Predicting sample size required for classification performance. _BMC Med. Inf. Decis. Mak._ 12,

8 (2012). Article  Google Scholar  * Dunn, W. B. & Ellis, D. I. Metabolomics: current analytical platforms and methodologies. _TrAC Trends Anal. Chem._ 24, 285–294 (2005). Article  CAS

  Google Scholar  * Chang, C.-Y. et al. Protein significance analysis in selected reaction monitoring (SRM) measurements. _Mol. Cell. Proteomics_ 11, M111.014662

https://doi.org/10.1074/mcp.M111.014662 (2012). * Markley, J. L. et al. The future of NMR-based metabolomics. _Curr. Opin. Biotechnol._ 43, 34–40 (2017). Article  CAS  PubMed  Google Scholar

  * Rocke, D. M. & Lorenzato, S. A two-component model for measurement error in analytical chemistry. _Technometrics_ 37, 176–184 (1995). Article  MATH  Google Scholar  * Van Batenburg,

M. F., Coulier, L., van Eeuwijk, F., Smilde, A. K. & Westerhuis, J. A. New figures of merit for comprehensive functional genomics data: the metabolomics case. _Anal. Chem._ 83, 3267–3274

(2011). Article  PubMed  CAS  Google Scholar  * Dunn, W. B. et al. Procedures for large-scale metabolic profiling of serum and plasma using gas chromatography and liquid chromatography

coupled to mass spectrometry. _Nat. Protoc._ 6, 1060–1083 (2011). Article  CAS  PubMed  Google Scholar  * Keun, H. C. _NMR-based Metabolomics_ P001–P368 (The Royal Society of Chemistry,

2018). * Tarazona, S., Garcia-Alcalde, F., Dopazo, J., Ferrer, A. & Conesa, A. Differential expression in RNA-seq: a matter of depth. _Genome Res._ 21, 2213–2223 (2011). Article  CAS 

PubMed  PubMed Central  Google Scholar  * Kim, S. et al. Evaluation and optimization of metabolome sample preparation methods for Saccharomyces cerevisiae. _Anal. Chem._ 85, 2169–2176

(2013). Article  CAS  PubMed  Google Scholar  * Köcher, T., Swart, R. & Mechtler, K. Ultra-high-pressure RPLC hyphenated to an LTQ-Orbitrap Velos reveals a linear relation between peak

capacity and number of identified peptides. _Anal. Chem._ 83, 2699–2704 (2011). Article  PubMed  CAS  Google Scholar  * Boja, E. S. & Rodriguez, H. Mass spectrometry-based targeted

quantitative proteomics: achieving sensitive and reproducible detection of proteins. _Proteomics_ 12, 1093–1110 (2012). Article  CAS  PubMed  Google Scholar  * Olkhov-Mitsel, E. & Bapat,

B. Strategies for discovery and validation of methylated and hydroxymethylated DNA biomarkers. _Cancer Med._ 1, 237–260 (2012). Article  CAS  PubMed  PubMed Central  Google Scholar  *

Armbruster, D. A. & Pry, T. Limit of blank, limit of detection and limit of quantitation. _Clin. Biochem. Rev._ 29, S49–S52 (2008). PubMed  PubMed Central  Google Scholar  * Arsova, B.,

Zauber, H. & Schulze, W. X. Precision, proteome coverage, and dynamic range of Arabidopsis proteome profiling using (15)N metabolic labeling and label-free approaches. _Mol. Cell.

Proteomics_ 11, 619–628 (2012). Article  CAS  PubMed  PubMed Central  Google Scholar  * Kuhn, E. et al. Interlaboratory evaluation of automated, multiplexed peptide immunoaffinity enrichment

coupled to multiple reaction monitoring mass spectrometry for quantifying proteins in plasma. _Mol. Cell. Proteomics_ 11, M111.013854 https://doi.org/10.1074/mcp.M111.013854 (2012). *

Kondrat, R. W., McClusky, G. A. & Cooks, R. G. Multiple reaction monitoring in mass spectrometry/mass spectrometry for direct analysis of complex mixtures. _Anal. Chem._ 50, 2017–2021

(1978). Article  CAS  Google Scholar  * Wishart, D. S. et al. HMDB: the human metabolome database. _Nucleic Acids Res._ 35, D521–D526 (2007). Article  CAS  PubMed  PubMed Central  Google

Scholar  * Kopka, J. et al. [email protected]: the golm metabolome database. _Bioinformatics_ 21, 1635–1638 (2005). Article  CAS  PubMed  Google Scholar  * Scholz, M. & Fiehn, O. SetupX–a

public study design database for metabolomic projects. _Pac. Symp. Biocomput_. 12, 169–180 (2007). * Bell, A. W. et al. A HUPO test sample study reveals common problems in mass

spectrometry-based proteomics. _Nat. Methods_ 6, 423–430 (2009). Article  CAS  PubMed  PubMed Central  Google Scholar  * Elias, J. E. & Gygi, S. P. Target-decoy search strategy for

increased confidence in large-scale protein identifications by mass spectrometry. _Nat. Methods_ 4, 207–214 (2007). Article  CAS  PubMed  Google Scholar  * Roberts, A., Feng, H. &

Pachter, L. Fragment assignment in the cloud with eXpress-D. _BMC Bioinformatics_14, 358 (2013). Article  CAS  Google Scholar  * Mortazavi, A., Williams, B. A., McCue, K., Schaeffer, L.

& Wold, B. Mapping and quantifying mammalian transcriptomes by RNA-Seq. _Nat. Methods_ 5, 621–628 (2008). Article  CAS  PubMed  Google Scholar  * Gomez-Cabrero, D. et al. STATegra, a

comprehensive multi-omics dataset of B-cell differentiation in mouse. _Sci. Data_ 6, 256 (2019). Article  PubMed  PubMed Central  Google Scholar  * Verhaak, R. G. W. et al. Integrated

genomic analysis identifies clinically relevant subtypes of glioblastoma characterized by abnormalities in PDGFRA, IDH1, EGFR, and NF1. _Cancer Cell_ 17, 98–110 (2010). Article  CAS  PubMed

  PubMed Central  Google Scholar  * Altmäe, S. et al. Guidelines for the design, analysis and interpretation of ‘omics’ data: focus on human endometrium. _Hum. Reprod. Update_ 20, 12–28

(2014). Article  PubMed  Google Scholar  * Reo, N. V. NMR-based Metabolomics. _Drug Chem. Toxicol._ 25, 375–382 (2002). Article  CAS  PubMed  Google Scholar  * Li, C.-I., Su, P.-F. &

Shyr, Y. Sample size calculation based on exact test for assessing differential expression analysis in RNA-seq data. _BMC Bioinformatics_ 14, 357–357 (2013). Article  PubMed  PubMed Central

  Google Scholar  * Storey, J. D. A direct approach to false discovery rates. _J. R. Stat. Soc. Ser. B_ 64, 479–498 (2002). Article  MathSciNet  MATH  Google Scholar  * Jung, S.-H. Sample

size for FDR-control in microarray data analysis. _Bioinformatics_ 21, 3097–3104 (2005). Article  CAS  PubMed  Google Scholar  * Storey, J. D. & Tibshirani, R. Estimating the positive

false discovery rate under dependence, with applications to DNA microarrays. _Stanford Stat. Rep._ 28 (2001). * Zhao, S., Li, C.-I., Guo, Y., Sheng, Q. & Shyr, Y. RnaSeqSampleSize: real

data based sample size estimation for RNA sequencing. _BMC Bioinformatics_ 19, 191 (2018). Article  PubMed  PubMed Central  CAS  Google Scholar  * Cohen, J. _Statistical Power Analysis for

the Behavioral Sciences_ (L. Erlbaum Associates, 1988). * Sawilowsky, S. New effect size rules of thumb. _J. Mod. Appl. Stat. Methods_ 8, 597–599 (2009). Article  Google Scholar  * Liu, P.

& Hwang, J. T. Quick calculation for sample size while controlling false discovery rate with application to microarray analysis. _Bioinformatics_ 23, 739–746 (2007). Article  CAS  PubMed

  Google Scholar  * Breiman, L. Random forests. _Mach. Learn._ 45, 5–32 (2001). Article  MATH  Google Scholar  * Rohart, F., Gautier, B., Singh, A. & Lê Cao, K.-A. mixOmics: An R package

for ‘omics feature selection and multiple data integration. _PLoS Comput. Biol._ 13, e1005752–e1005752 (2017). Article  ADS  PubMed  PubMed Central  CAS  Google Scholar  * James, G.,

Witten, D., Hastie, T. & Tibshirani, R. _An Introduction to Statistical Learning_ Vol. 112 (Springer, 2013). * Friedman, J. H., Hastie, T. & Tibshirani, R. Regularization paths for

generalized linear models via coordinate descent. _J. Stat. Softw._ 33, 1–22 (2010). * Meyer, M. C. Inference using shape-restricted regression splines. _Ann. Appl. Stat._ 2, 1013–1033

(2008). Article  MathSciNet  MATH  Google Scholar  * Ramsay, J. O. Monotone regression splines in action. _Stat. Sci._ 3, 425–441 (1988). Article  Google Scholar  Download references

ACKNOWLEDGEMENTS This work has been funded by FP7 STATegra project agreement 306000 and Spanish MINECO grant BIO2012–40244. In addition, work in the Imhof lab has been funded by the (DFG;

CIPSM and SFB1064). The work of L.B.-N. has been funded by the University of Florida Startup funds. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Applied Statistics, Operations

Research and Quality, Universitat Politècnica de València, Valencia, Spain Sonia Tarazona * Microbiology and Cell Science Department, Institute for Food and Agricultural Research,

University of Florida, Gainesville, FL, USA Leandro Balzano-Nogueira & Ana Conesa * Unit of Computational Medicine, Department of Medicine, Solna, Center for Molecular Medicine,

Karolinska Institutet, Stockholm, Sweden David Gómez-Cabrero & Jesper Tegnér * Science for Life Laboratory, Solna, Sweden David Gómez-Cabrero & Jesper Tegnér * Mucosal & Salivary

Biology Division, King’s College London Dental Institute, London, UK David Gómez-Cabrero * Navarrabiomed, Complejo Hospitalario de Navarra (CHN), Universidad Pública de Navarra (UPNA),

IdiSNA, Pamplona, Spain David Gómez-Cabrero * Protein Analysis Unit, Biomedical Center, Faculty of Medicine, LMU Munich, Planegg-Martinsried, Germany Andreas Schmidt & Axel Imhof *

Munich Center of Integrated Protein Science LMU Munich, Planegg-Martinsried, Germany Axel Imhof * Division Analytical Biosciences, Leiden/Amsterdam Center for Drug Research, Leiden, The

Netherlands Thomas Hankemeier * Biological and Environmental Sciences and Engineering Division, Computer, Electrical and Mathematical Sciences and Engineering Division, King Abdullah

University of Science and Technology, Thuwal, Saudi Arabia Jesper Tegnér * Swammerdam Institute for Life Sciences, University of Amsterdam, Amsterdam, The Netherlands Johan A. Westerhuis *

Department of Statistics, Faculty of Natural Sciences, North-West University (Potchefstroom Campus), Potchefstroom, South Africa Johan A. Westerhuis * Genetics Institute, University of

Florida, Gainesville, FL, USA Ana Conesa Authors * Sonia Tarazona View author publications You can also search for this author inPubMed Google Scholar * Leandro Balzano-Nogueira View author

publications You can also search for this author inPubMed Google Scholar * David Gómez-Cabrero View author publications You can also search for this author inPubMed Google Scholar * Andreas

Schmidt View author publications You can also search for this author inPubMed Google Scholar * Axel Imhof View author publications You can also search for this author inPubMed Google Scholar

* Thomas Hankemeier View author publications You can also search for this author inPubMed Google Scholar * Jesper Tegnér View author publications You can also search for this author

inPubMed Google Scholar * Johan A. Westerhuis View author publications You can also search for this author inPubMed Google Scholar * Ana Conesa View author publications You can also search

for this author inPubMed Google Scholar CONTRIBUTIONS S.T.: contributed to FOM analysis, implemented and tested MultiPower method, and drafted the manuscript; L.B.-N.: implemented and tested

the MultiML method, and drafted the manuscript; D.G.-C: contributed to FOM analysis, tested MultiPower, and MultiML methods; A.S.: contributed to FOM analysis of proteomics data; A.I.:

contributed to FOM analysis of proteomics data; T.H.: discussed FOM analysis of metabolomics data; J.T.: supervised parts of the work; J.A.W.: contributed to FOM definition and analysis; and

A.C.: supervised, coordinated the work, and drafted the manuscript. All authors contributed to and approved the final version of the manuscript. CORRESPONDING AUTHOR Correspondence to Ana

Conesa. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PEER REVIEW INFORMATION _Nature Communications_ thanks Timothy Ebbels,

Daniel Rotroff and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional

claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION REPORTING SUMMARY RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed

under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate

credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article

are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and

your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this

license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Tarazona, S., Balzano-Nogueira, L., Gómez-Cabrero, D. _et al._

Harmonization of quality metrics and power calculation in multi-omic studies. _Nat Commun_ 11, 3092 (2020). https://doi.org/10.1038/s41467-020-16937-8 Download citation * Received: 27 July

2018 * Accepted: 29 May 2020 * Published: 18 June 2020 * DOI: https://doi.org/10.1038/s41467-020-16937-8 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this

content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative