Understanding rate effects in injection-induced earthquakes

ABSTRACT Understanding the physical mechanisms that underpin the link between fluid injection and seismicity is essential in efforts to mitigate the seismic risk associated with subsurface

technologies. To that end, here we develop a poroelastic model of earthquake nucleation based on rate-and-state friction in the manner of spring–sliders, and analyze conditions for the

emergence of stick-slip frictional instability—the mechanism for earthquakes—by carrying out a linear stability analysis and nonlinear simulations. We find that the likelihood of triggering

earthquakes depends largely on the rate of increase in pore pressure rather than its magnitude. Consequently, fluid injection at constant rate acts in the direction of triggering seismic

rupture at early times followed by aseismic creep at late times. Our model implies that, for the same cumulative volume of injected fluid, an abrupt high-rate injection protocol is likely to

increase the seismic risk whereas a gradual step-up protocol is likely to decrease it. SIMILAR CONTENT BEING VIEWED BY OTHERS INTERDEPENDENT EFFECTS OF FLUID INJECTION PARAMETERS ON

TRIGGERED ASEISMIC SLIP AND SEISMICITY Article Open access 03 December 2022 ROLE OF CRITICAL STRESS IN QUANTIFYING THE MAGNITUDE OF FLUID-INJECTION TRIGGERED EARTHQUAKES Article Open access

10 September 2024 THE PHYSICAL MECHANISMS OF INDUCED EARTHQUAKES Article 05 December 2023 INTRODUCTION Subsurface fluid-injection operations have been recognized to carry a risk of inducing

earthquakes since the 1960s1. While most of the injection-induced earthquakes are micro-tremors, they can occasionally be of large magnitude, such as the Prague _M_w 5.7 earthquake in 20112,

the Pawnee _M_w 5.8 earthquake in 20163, and the Pohang _M_w 5.5 earthquake in 20174, among others. The occurrence of induced earthquakes of large magnitude has motivated development of

different operational strategies for seismic hazard mitigation. In particular, an early attempt to control seismicity at the Rangely oil field suggested maintaining the magnitude of fluid

pressure below a critical threshold5, based on a Coulomb failure model that links the magnitude of fluid pressure to the occurrence of induced earthquakes6. This model, however, does not

address the evolution of the rupture and whether a fault slips seismically or aseismically. It was also insufficient to explain seismicity at Cogdell oil field, for instance, where

earthquakes were observed in regions of low rather than high fluid pressure7. A different strategy to control seismicity involved maintaining the cumulative volume of injected fluid below a

critical threshold8, based on empirical observations and modeling linking the cumulative volume of injected fluid to the maximum magnitude of induced earthquakes9. This model, however, is at

odds with the 2017 Pohang earthquake, as its magnitude exceeded the size estimated from the injected volume by 500 times10. A growing number of field observations suggests that managing

fluid injection rates may be a promising tool to mitigate the occurrence of induced earthquakes. It is observed that low-rate wells, for instance, are much less likely to be associated with

earthquakes than high-rate wells, and that the critical rate above which earthquakes are induced is likely dependent on reservoir properties11,12. It is also observed that temporal variation

in injection rates is generally correlated with the frequency of earthquakes1,13,14,15, and that abrupt increases in injection rates tend to shortly precede the occurrence of

earthquakes16,17,18. While attempts have been made to explain some of these observations with seismicity-rate models19,20,21 and 2D numerical simulations of coupled flow-geomechanics22,23,

the physical mechanisms behind the link between the rate of fluid injection and the occurrence of induced earthquakes remain poorly understood. Seismicity-rate models based on the

triggering-front concept consider the large-scale spatiotemporal effects of nonlinear diffusion on the probability of a given magnitude earthquake using Gutenberg–Richter statistics24, but

do not address the dynamics of the rupture and, in particular, whether a fault slips seismically or aseismically. Characterizing fault slip mode is essential to mitigate the seismic risk

associated with subsurface operations, as it has been observed that an increase in pore pressure magnitude leads to seismic slip in some sites1,2,3,4,5,25 and aseismic slip in

others7,26,27,28,29,30. Here we develop a poroelastic model of induced earthquake nucleation in the manner of spring–sliders31,32,33,34,35 based on rate-and-state friction32,36, and we study

the effect of injection rate on stick-slip frictional behavior—the mechanism for seismic slip37. Our model shows that the likelihood of triggering earthquakes depends critically on the rate

of increase in pore pressure. We find that fluid injection at constant rate acts in the direction of triggering seismic rupture at early times followed by aseismic creep at late times. This

finding is qualitatively consistent with laboratory observations of sliding between saturated rocks at both transient and steady-state pore pressure conditions38,39,40, and may explain

field observations of triggered and induced seismicity from subsurface operations in different geologic settings1,11,12,13,14,16,17,18. RESULTS AND DISCUSSION POROELASTIC SPRING–SLIDER MODEL

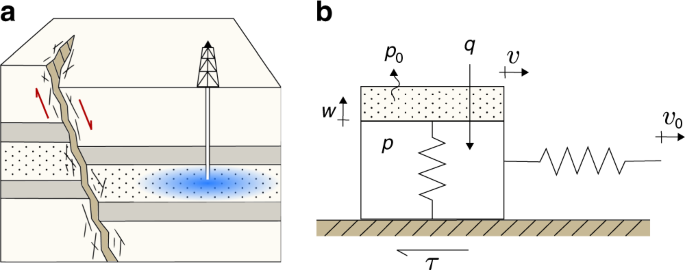
When fluid is injected into a faulted reservoir, the pore pressure change induces effective stress variations in the reservoir and surrounding rock (Fig. 1a). To model the effects of

variations in effective normal stress on a creeping fault segment, we develop a poroelastic spring–slider model of frictional slip (Fig. 1b). Our model consists of a slider of unit base area

that is pulled by a spring whose end is constrained to move at a steady slip rate. The spring stiffness accounts for the elastic interaction of the sliding surface with the surrounding

rock. The slider represents the injection-driven deformation process, where a piston is loaded vertically and compresses a spring inside a fluid-filled space. The vertical spring is

analogous to the rock skeleton, while the fluid inside the slider represents fluid in the rock pores subject to increase from fluid injection and decrease from pressure diffusion. Our model

accounts for the poroelastic coupling between the shear and effective normal stresses along the fault. Frictional evolution is modeled by the rate-and-state constitutive laws32,36, which are

capable of reproducing a wide range of observed seismic and aseismic fault behaviors ranging from preseismic slip and earthquake nucleation to coseismic rupture and earthquake afterslip41.

These laws propose that the frictional shear stress is a function of the effective normal stress and a coefficient of friction that is dependent on slip rate and the state of the sliding

surface. Since the effective normal stress varies as a result of fluid injection, we adopt Linker and Dieterich’s42 formulation for the coefficient of friction and couple it with a

poroelastic model of pore pressure and rock deformation. We derive the poroelastic model from the principles of mass and momentum conservation, and find that pore pressure satisfies a

diffusion equation that leads to transient behavior at early times and steady-state behavior at late times. The dimensional equations describing the dynamic motion of the poroelastic

spring–slider system with an evolving pore pressure take the form (see Supplementary Note 1 for the derivation of the equations): $$\dot{U}={V}_{0}-V,$$ (1) $$\dot{V}=\frac{1}{{\left(T/2\pi

\right)}^{2}}\left[U-\frac{1}{{k}_{{\rm{s}}}} \left({\mu }_{* }+\hat{a}{\,}{\mathrm{ln}}\,\frac{V}{{V}_{* }}+\Theta \right)(\Sigma -P)\right],$$ (2) $${\dot{\Theta

}}=-\frac{V}{{d}_{{\rm{c}}}} \left(\Theta +{\hat{b}}{\,}{\mathrm{ln}}\,\frac{V}{{V}_{* }} \right)+{\hat{\alpha }}\frac{{\dot{P}}}{(\Sigma -P)},$$ (3)

$$\dot{P}=\frac{{k}_{{\rm{n}}}^{{\rm{eff}}}k}{\eta L}({P}_{0}-P)+{k}_{{\rm{n}}}^{{\rm{eff}}}Q.$$ (4) where _U_ is the relative displacement between the load point and the slider,

\({\dot{\,\,( )}}\) denotes time derivative, _V_0 is the loading velocity, _V_ is slip rate, _T_ is the vibration period, _k_s is the shear stiffness, _V_* is a normalizing slip rate, _μ_*

is a constant appropriate for steady-state at slip rate _V_*, \(\hat{a}\) and \(\hat{b}\) are experimentally derived parameters relating friction to changes in slip rate and state,

respectively, Θ is a state variable describing the sliding surface, Σ is the total stress, _P_ is the pressure inside the slider (pore pressure), _d_c is the characteristic slip distance,

\(\hat{\alpha }\) is a scaling factor ranging from 0 to _μ_42,43, \({k}_{{\rm{n}}}^{{\rm{eff}}}\) is the effective normal stiffness (related to the uniaxial bulk modulus or the reciprocal of

the uniaxial specific storage per diffusion length in a continuum), _k_ is the permeability, _η_ is fluid dynamic viscosity, _L_ is the pressure diffusion length, _P_0 is the ambient

pressure, and _Q_ is the volumetric injection rate per unit area. Choosing the following characteristic quantities: _u_c = _d_c, _v_c = _V_*, _μ_c = _μ_*, _p_c = _P_0, _τ_c = _μ_*(Σ − _P_0),

_θ_c = _μ_*, and _t_c = _d_c/_V_*, the equations describing the dynamic motion of the system, in dimensionless form, become (see Supplementary Note 2): $$\dot{u}={v}_{0}-v,$$ (5)

$$\dot{v}=\frac{1}{{\epsilon }^{2}}\left[u-\frac{1}{\kappa } (1+a{\,}{\mathrm{ln}}\,v+\theta )(\sigma -p)\right],$$ (6) $${\dot{\theta }}=-v(\theta +b{\,}{\mathrm{ln}}\,v)+\alpha

\frac{{\dot{p}}}{(\sigma -p)},$$ (7) $$\dot{p}=c({p}_{0}-p)+rq,$$ (8) where _κ_ = (_k_s_d_c)/_τ_c, \(a=\hat{a}/{\mu }_{{\rm{c}}}\), \(b=\hat{b}/{\mu }_{{\rm{c}}}\), \(\alpha =\hat{\alpha

}/{\mu }_{{\rm{c}}}\), _ϵ_ = (_T_/2_π_)/_t_c, \(c={t}_{{\rm{c}}}/(\eta L/{k}_{{\rm{n}}}^{{\rm{eff}}}/k)\), \(r={t}_{{\rm{c}}}{k}_{{\rm{n}}}^{{\rm{eff}}}\), and _q_ = _Q_/_p_c. The parameter

_κ_ is the normalized shear stiffness, and _a_, _b_, _α_ are normalized frictional parameters. The parameter _ϵ_ is the normalized oscillation period or ratio of inertial to state-evolution

timescales, which may range from 10−8 to 10−6 depending on rupture diameter and shear wave speed. The parameter _c_ is the normalized diffusivity or ratio of the pore pressure to the

state-evolution timescales, which may range from 10−4 to 101 depending on reservoir permeability, uniaxial bulk modulus, and well-fault distance. The parameter rq is the normalized injection

rate, which may range from 10−5 to 10−1 depending on injection rate and reservoir size. STABILITY ANALYSIS The stability of steady frictional sliding to small perturbations in velocity,

which determines whether motion is by slow steady-sliding or violent stick-slip, depends on the evolution of the frictional resistance. Stick-slip occurs whenever a change of frictional

resistance with sliding occurs at a rate greater than the loading system is capable of following31. At a constant pore pressure, linear stability analysis of the system about steady-state

leads to the stability condition by Ruina32. Pore pressure, however, is not constant in time and its evolution depends on the injection rate and on the poroelastic and hydraulic parameters

of the rupture. To quantify this, we carry out a linear stability analysis of the system about a quasi steady-state where sliding is steady but pore pressure is evolving as a result of fluid

injection. We find that motion is by stick-slip when the dimensionless shear stiffness of the loading system is lower than a critical value (_κ_ < _κ_crit) given by $${\kappa

}_{{\rm{crit}}}=(b-a)(\sigma -p)+\frac{\alpha }{{v}_{0}}\dot{p},$$ (9) and is by steady-sliding otherwise (_κ_ > _κ_crit). Variables _p_ and \(\dot{p}\) are dimensionless pore pressure

magnitude and pore pressure rate, respectively, at any point in time. Accordingly, frictional instability for the spring–poroslider system with an evolving pore pressure depends not only on

the magnitude of pore pressure, but also on the rate of change of pore pressure (Supplementary Notes 3, 4, 5, and 6 for the analysis of QSSA, derivation of Eq. (9), and validation against

nonlinear simulations). As pore pressure evolves from initial to steady-state conditions in response to fluid injection, we find that the competing effects of _p_ and \(\dot{p}\) exhibit a

transition in their dominance over frictional instability (Fig. 2a). The destabilizing effect of \(\dot{p}\) dominates when pore pressure grows rapidly at early times, resulting in an

increase in critical stiffness (dashed curve in Fig. 2a). It then decreases as pore pressure diffuses and approaches steady state, giving rise to the stabilizing effect of _p_, which

explains the decrease in critical stiffness at late times (dotted curve in Fig. 2a). This result is generally consistent with a linear stability analysis of slow slip with mildly

rate-strengthening friction in a poroelastic continuum44, in which undrained slip-induced poroelastic pressure has a destabilizing effect and a sufficiently fast equilibration process has a

stabilizing effect. In our analysis, the early-time destabilizing effect of \(\dot{p}\) is likely attributed to a short-term effect on contact interlocking, where a decrease in effective

normal stress results in fault opening and loss of asperity contacts45. The late-time stabilizing effect of _p_, in contrast, is likely attributed to a long-term effect on interface locking.

A low effective normal stress tends to reduce the degree of interface locking, and thus limit the magnitude of stress drops46,47,48. This behavior is also qualitatively consistent with

laboratory observations of sliding between saturated rocks at both transient and steady-state pore pressure conditions. The early-time destabilizing effect agrees with experimental studies

showing that a gradual increase in pore pressure results in unstable slip during the transient-state, and that the degree of instability measured by the total slip, slip rate, and shear

stress drop correlates with the rate of pore pressure increase38,39. The late-time stabilizing effect also agrees with another experimental study, showing that sliding between two rock

surfaces is much more stable at high than at low steady-state pore pressure40. Sliding is observed to be by slow, steady-type motion at high pore pressure, and by stick-slip at low pore

pressure. This behavior, however, is different from the observations of shearing granular fault gouge materials49,50, where the frictional parameter _a_−_b_ is observed to decrease in

magnitude with increasing steady-state pore pressure, an effect related to shear-induced dilatancy strengthening and pore compaction creep. APPLICATION TO THE DENVER EARTHQUAKES Our

findings, if they are applicable to natural faults, hold interesting and important implications for induced seismicity. The poroelastic spring–slider may be viewed as a simple model of a

fault segment in contact with a reservoir, steady-sliding as an analog of aseismic creep, and stick-slip as a seismic wave-producing rupture cycle33,37. The spring stiffness scales inversely

with the size of the fault segment51. Within this view, our findings may be generalized to indicate that a slowly creeping fault segment is destabilized and nucleates an earthquake if its

size exceeds a critical value known as the nucleation length, which is inversely proportional to the critical stiffness in Eq. (9). To bridge the gap between the analysis of the idealized

poroelastic spring–slider model and the real world, we extend our instability criterion from dimensionless to dimensional form, and identify values of dimensionless parameters _c_ and rq

that correspond to a real-world setting. The 1960s Denver earthquakes is a good example of a real-world setting, where it is well-documented that injection of wastewater into the fractured

Precambrian granite gneiss underneath the Rocky Mountain Arsenal triggered the earthquakes and where injection rate is directly related to the frequency of earthquakes52,53. We find that

reasonable estimates of _c_ and rq for this setting are in the order of 10−2 to 10−1 and 10−3 to 10−1, respectively. We then assess the effect of fluid pressurization by evaluating its

contribution to the critical stiffness in Eq. (9). We find that a reasonable estimate for the increase in critical stiffness at early times is ~300%, which indicates that the weakening

effect from fluid pressurization is likely significant in this setting (see Supplementary Note 7 for more details on the application to the Denver earthquakes). When earthquakes nucleate on

a fault with velocity-weakening friction, in general, aseismic creep may begin in sections of favorable stress conditions. The aseismically creeping segment then slowly grows in size until

it reaches the nucleation length, and then it breaks out rapidly into a seismic wave-producing rupture54. A significant increase in critical stiffness, or equivalently decrease in nucleation

length, from fluid pressurization may further facilitate or exacerbate this breakout—potentially increasing the likelihood of triggering earthquakes. INFLUENCE OF RESERVOIR PROPERTIES ON

INJECTION-INDUCED SEISMICITY To study the influence of reservoir properties on the critical injection rate, above which earthquakes are induced, we model the occurrence of earthquakes as a

function of dimensionless injection rate \(rq={d}_{{\rm{c}}}{k}_{{\rm{n}}}^{{\rm{eff}}}Q/({p}_{{\rm{c}}}{V}_{* })\) and normalized diffusivity

\(c={d}_{{\rm{c}}}{k}_{{\rm{n}}}^{{\rm{eff}}}k/(\eta L{V}_{* })\) for velocity-weakening conditions, _b_ − _a_ > 0. We find that the dimensionless critical injection rate is directly

proportional to the diffusivity _c_ in the high-diffusivity limit, and independent of it in the low-diffusivity limit (Fig. 2b). These findings suggest that reservoir regions with low

hydraulic diffusivity are more prone to induced seismicity than regions with high hydraulic diffusivity—a result that qualitatively agrees with the triggering-front concept24 (see

Supplementary Note 8 for more details on the phase diagram of injection-induced seismicity). INFLUENCE OF INJECTION STRATEGY ON INDUCED SEISMICITY The earthquake likelihood is strongly

dependent on the duration of injection. For a fixed total injected volume, a shorter injection duration (or, equivalently, a higher injection rate) results in a higher likelihood of

earthquake triggering (Supplementary Note 9). To further understand how injection rate may be used to minimize or mitigate the seismic hazard, we simulate three different injection

scenarios, and examine the stability of each. Figure 3 demonstrates how injecting the same volume of fluid can have very different seismic potential depending on the injection profile. We

observe that injecting at constant rate in scenario (A) causes the critical stiffness to increase at early times, potentially triggering earthquakes, and decrease at late times, potentially

resulting in the cessation of earthquakes. In addition, we observe a dramatic drop in critical stiffness upon stopping injection followed by recovery to the value prior to injection.

Scenario (B) shows that a higher injection rate yields higher critical stiffness, implying an increased risk of seismicity for this higher injection rate. Scenario (C), where the injection

rate ramps up in stages, seems to be most stable because the maximum critical stiffness is lower than its value in both (A) and (B). If the duration of each stage is not sufficiently long

for pressure to stabilize at the fault, the ramp-up injection strategy does not counteract the destabilizing effect of the rate of pore pressure increase at each injection rate increment. In

the Basel enhanced geothermal site, for example, the duration of injection stages was 1 day55, while the time for pressure to stabilize at the fault is longer than 1 month—a conservative

estimate based on the distance to the nearest fault segment to the injection well and the permeability of the fractured rock25,55. This suggests that a gradual increase in injection rate,

where pore pressure is allowed to stabilize between injection stages, may be the safest injection strategy. SUMMARY AND OUTLOOK In summary, our model points to the underlying mechanism by

which the rate of fluid pressurization, and hence the rate of effective normal stress unloading, may explain several injection-induced seismicity observations1,11,12,13,14,16,17,18. An

abrupt or large increase in injection rate tends to intensify the early-time destabilizing effect of the rate of change in pore pressure on frictional sliding, whereas a gradual or small

increase in injection rate tends to lessen it. Our findings, as a whole, suggest injection strategies to mitigate the seismic risk associated with a wide range of subsurface operations, from

wastewater injection to geologic CO2 sequestration. Of course, a complex interplay of different mechanisms such as heterogeneous fault stresses, stress changes from aseismic slip, spatial

growth of pore pressure diffusion, and static and dynamic stress transfer often play a role in the occurrence and, in particular, the timing of an earthquake4. This emphasizes the need to

continue to develop and test new models for the forecast and control of induced seismicity10. METHODS METHODS DESCRIBED IN THE SUPPLEMENTARY INFORMATION All methods and data are described in

the Supplementary Information, including: (1) Derivation of the poroelastic spring–slider equations; (2) Governing equations in dimensionless form; (3) Linear stability analysis; (4)

Nonlinear simulations; (5) Analytical vs. numerical estimates of critical stiffness; (6) Detailed discussion on the quasi-steady-state approximation; (7) Application to the Denver

earthquakes; (8) Phase diagram of injection-induced seismicity; and (9) Earthquake likelihood vs. injection duration. DATA AVAILABILITY All relevant data are available upon reasonable

request from the authors. CODE AVAILABILITY The simulation code is available upon reasonable request from the authors. REFERENCES * Healy, J., Rubey, W., Griggs, D. & Raleigh, C. The

Denver earthquakes. _Science_ 161, 1301–1310 (1968). Article  ADS  CAS  PubMed  Google Scholar  * Keranen, K. M., Weingarten, M., Abers, G. A., Bekins, B. A. & Ge, S. Sharp increase in

central Oklahoma seismicity since 2008 induced by massive wastewater injection. _Science_ 345, 448–451 (2014). Article  ADS  CAS  PubMed  Google Scholar  * Yeck, W. L. et al. Oklahoma

experiences largest earthquake during ongoing regional wastewater injection hazard mitigation efforts. _Geophys. Res. Lett._ 44, 711–717 (2017). Article  ADS  Google Scholar  * Grigoli, F.

et al. The November 2017 Mw 5.5 Pohang earthquake: a possible case of induced seismicity in South Korea. _Science_ 360, 1003–1006 (2018). Article  ADS  CAS  PubMed  Google Scholar  *

Raleigh, C., Healy, J. & Bredehoeft, J. An experiment in earthquake control at Rangely, Colorado. _Science_ 191, 1230–1237 (1976). Article  ADS  CAS  PubMed  Google Scholar  * Hubbert,

K. M. & Rubey, W. W. Role of fluid pressure in mechanics of overthrust faulting: I. mechanics of fluid-filled porous solids and its application to overthrust faulting. _Geol. Soc. Am.

Bull._ 70, 115–166 (1959). Article  ADS  Google Scholar  * Davis, S. D. & Pennington, W. D. Induced seismic deformation in the Cogdell oil field of West Texas. _Bull. Seismol. Soc. Am._

79, 1477–1495 (1989). Google Scholar  * Hofmann, H. et al. First field application of cyclic soft stimulation at the Pohang Enhanced Geothermal System site in Korea. _Geophys. J. Int._ 217,

926–949 (2019). Article  ADS  Google Scholar  * McGarr, A. Maximum magnitude earthquakes induced by fluid injection. _J. Geophys. Res. Solid Earth_ 119, 1008–1019 (2014). Article  ADS 

Google Scholar  * Lee, K.-K. et al. Managing injection-induced seismic risks. _Science_ 364, 730–732 (2019). Article  ADS  CAS  PubMed  Google Scholar  * Frohlich, C. Two-year survey

comparing earthquake activity and injection-well locations in the Barnett Shale, Texas. _Proc. Natl Acad. Sci. USA_ 109, 13934–13938 (2012). Article  ADS  CAS  PubMed  Google Scholar  *

Weingarten, M., Ge, S., Godt, J. W., Bekins, B. A. & Rubinstein, J. L. High-rate injection is associated with the increase in US mid-continent seismicity. _Science_ 348, 1336–1340

(2015). Article  ADS  CAS  PubMed  Google Scholar  * Improta, L., Valoroso, L., Piccinini, D. & Chiarabba, C. A detailed analysis of wastewater-induced seismicity in the Val d’Agri oil

field (Italy). _Geophys. Res. Lett._ 42, 2682–2690 (2015). Article  ADS  Google Scholar  * Langenbruch, C. & Zoback, M. D. How will induced seismicity in Oklahoma respond to decreased

saltwater injection rates? _Sci. Adv._ 2, e1601542 (2016). Article  ADS  PubMed  PubMed Central  Google Scholar  * Barbour, A. J., Norbeck, J. H. & Rubinstein, J. L. The effects of

varying injection rates in Osage County, Oklahoma, on the 2016 Mw 5.8 Pawnee earthquake. _Seismol. Res. Lett._ 88, 1040–1053 (2017). Article  Google Scholar  * Cuenot, N., Dorbath, C. &

Dorbath, L. Analysis of the microseismicity induced by fluid injections at the EGS site of Soultz-sous-Forêts (Alsace, France): implications for the characterization of the geothermal

reservoir properties. _Pure Appl. Geophys._ 165, 797–828 (2008). Article  ADS  Google Scholar  * Kim, W.-Y. Induced seismicity associated with fluid injection into a deep well in Youngstown,

Ohio. _J. Geophys. Res. Solid Earth_ 118, 3506–3518 (2013). Article  ADS  Google Scholar  * Tang, L., Lu, Z., Zhang, M., Sun, L. & Wen, L. Seismicity induced by simultaneous abrupt

changes of injection rate and well pressure in Hutubi gas field. _J. Geophys. Res. Solid Earth_ 123, 5929–5944 (2018). Article  ADS  Google Scholar  * Langenbruch, C., Weingarten, M. &

Zoback, M. D. Physics-based forecasting of man-made earthquake hazards in Oklahoma and Kansas. _Nat. Commun._ 9, 3946 (2018). Article  ADS  PubMed  PubMed Central  CAS  Google Scholar  *

Norbeck, J. & Rubinstein, J. L. Hydromechanical earthquake nucleation model forecasts onset, peak, and falling rates of induced seismicity in Oklahoma and Kansas. _Geophys. Res. Lett._

45, 2963–2975 (2018). Article  ADS  Google Scholar  * Zhai, G., Shirzaei, M., Manga, M. & Chen, X. Pore-pressure diffusion, enhanced by poroelastic stresses, controls induced seismicity

in Oklahoma. _Proc. Natl Acad. Sci. USA_ 116, 16228–16233 (2019). Article  ADS  CAS  PubMed  Google Scholar  * Torberntsson, K., Stiernström, V., Mattsson, K. & Dunham, E. M. A finite

difference method for earthquake sequences in poroelastic solids. _Comput. Geosci._ 22, 1351–1370 (2018). Article  MATH  MathSciNet  Google Scholar  * Pampillón, P., Santillán, D., Mosquera,

J. C. & Cueto-Felgueroso, L. Dynamic and quasi-dynamic modeling of injection-induced earthquakes in poroelastic media. _J. Geophys. Res. Solid Earth_ 123, 5730–5759 (2018). Article  ADS

  Google Scholar  * Shapiro, S. & Dinske, C. Scaling of seismicity induced by nonlinear fluid-rock interaction. _J. Geophys. Res. Solid Earth_ https://doi.org/10.1029/2008JB006145

(2009). * Majer, E. L. et al. Induced seismicity associated with enhanced geothermal systems. _Geothermics_ 36, 185–222 (2007). Article  Google Scholar  * Guglielmi, Y., Cappa, F., Avouac,

J.-P., Henry, P. & Elsworth, D. Seismicity triggered by fluid injection–induced aseismic slip. _Science_ 348, 1224–1226 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Cornet, F.,

Helm, J., Poitrenaud, H. & Etchecopar, A. Seismic and aseismic slips induced by large-scale fluid injections. _Pure Appl. Geophys._ 150, 563–583 (1997). Article  ADS  Google Scholar  *

Bourouis, S. & Bernard, P. Evidence for coupled seismic and aseismic fault slip during water injection in the geothermal site of Soultz (France), and implications for seismogenic

transients. _Geophys. J. Int._ 169, 723–732 (2007). Article  ADS  Google Scholar  * Zoback, M. D. et al. The importance of slow slip on faults during hydraulic fracturing stimulation of

shale gas reservoirs. _In SPE Americas Unconventional Resources Conference_ (Society of Petroleum Engineers, 2012). * Wei, S. et al. The 2012 Brawley swarm triggered by injection-induced

aseismic slip. _Earth Planet. Sci. Lett._ 422, 115–125 (2015). Article  ADS  CAS  Google Scholar  * Byerlee, J. The mechanics of stick-slip. _Tectonophysics_ 9, 475–486 (1970). Article  ADS

  Google Scholar  * Ruina, A. Slip instability and state variable friction laws. _J. Geophys. Res. Solid Earth_ 88, 10359–10370 (1983). Article  Google Scholar  * Rice, J. R. & Tse, S.

T. Dynamic motion of a single degree of freedom system following a rate and state dependent friction law. _J. Geophys. Res. Solid Earth_ 91, 521–530 (1986). Article  Google Scholar  *

Segall, P. & Rice, J. R. Dilatancy, compaction, and slip instability of a fluid-infiltrated fault. _J. Geophys. Res. Solid Earth_ 100, 22155–22171 (1995). Article  Google Scholar  *

Iverson, R. M. Regulation of landslide motion by dilatancy and pore pressure feedback. _J. Geophys. Res. Earth Surf._ 110, F02015 (2005). Article  ADS  Google Scholar  * Dieterich, J. H.

Modeling of rock friction: 1. Experimental results and constitutive equations. _J. Geophys. Res. Solid Earth_ 84, 2161–2168 (1979). Article  Google Scholar  * Brace, W. & Byerlee, J.

Stick-slip as a mechanism for earthquakes. _Science_ 153, 990–992 (1966). Article  ADS  CAS  PubMed  Google Scholar  * Wang, L. et al. Laboratory study on fluid-induced fault slip behavior:

The role of fluid pressurization rate. _Geophys. Res. Lett._ 47, e2019GL086627 (2020). ADS  Google Scholar  * French, M. E., Zhu, W. & Banker, J. Fault slip controlled by stress path and

fluid pressurization rate. _Geophys. Res. Lett._ 43, 4330–4339 (2016). Article  ADS  Google Scholar  * Byerlee, J. & Brace, W. Fault stability and pore pressure. _Bull. Seismol. Soc.

Am._ 62, 657–660 (1972). Google Scholar  * Marone, C. Laboratory-derived friction laws and their application to seismic faulting. _Annu. Rev. Earth Planet. Sci._ 26, 643–696 (1998). Article

  ADS  CAS  Google Scholar  * Linker, M. & Dieterich, J. H. Effects of variable normal stress on rock friction: observations and constitutive equations. _J. Geophys. Res. Solid Earth_

97, 4923–4940 (1992). Article  Google Scholar  * Kilgore, B., Lozos, J., Beeler, N. & Oglesby, D. Laboratory observations of fault strength in response to changes in normal stress. _J.

Appl. Mech._ 79, 031007 (2012). Article  ADS  Google Scholar  * Heimisson, E. R., Dunham, E. M. & Almquist, M. Poroelastic effects destabilize mildly rate-strengthening friction to

generate stable slow slip pulses. _J. Mech. Phys. Solids_ 130, 262–279 (2019). Article  ADS  MathSciNet  Google Scholar  * Wang, W. & Scholz, C. Micromechanics of the velocity and normal

stress dependence of rock friction. _Pure Appl. Geophys._ 143, 303–315 (1994). Article  ADS  Google Scholar  * Moreno, M., Rosenau, M. & Oncken, O. 2010 Maule earthquake slip correlates

with pre-seismic locking of Andean subduction zone. _Nature_ 467, 198–202 (2010). Article  ADS  CAS  PubMed  Google Scholar  * Kitajima, H. & Saffer, D. M. Elevated pore pressure and

anomalously low stress in regions of low frequency earthquakes along the Nankai Trough subduction megathrust. _Geophys. Res. Lett._ 39, L23301 (2012). Article  ADS  Google Scholar  * Segall,

P., Rubin, A. M., Bradley, A. M. & Rice, J. R. Dilatant strengthening as a mechanism for slow slip events. _J. Geophys. Res. Solid Earth_ https://doi.org/10.1029/2010JB007449 (2010). *

Sawai, M., Niemeijer, A. R., Plümper, O., Hirose, T. & Spiers, C. J. Nucleation of frictional instability caused by fluid pressurization in subducted blueschist. _Geophys. Res. Lett._

43, 2543–2551 (2016). Article  ADS  Google Scholar  * Scuderi, M. M. & Collettini, C. The role of fluid pressure in induced vs. triggered seismicity: Insights from rock deformation

experiments on carbonates. _Sci. Rep._ 6, 24852 (2016). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Scholz, C. H. Earthquakes and friction laws. _Nature_ 391, 37 (1998).

Article  ADS  CAS  Google Scholar  * Evans, D. M. The Denver area earthquakes and the Rocky Mountain Arsenal disposal well. _Mt. Geologist_ 3, 23–36 (1966). Google Scholar  * Healy, J.,

Rubey, W., Griggs, D. & Raleigh, C. The Denver earthquakes. _Science_ 161, 1301–1310 (1968). Article  ADS  CAS  PubMed  Google Scholar  * Perfettini, H., Schmittbuhl, J., Rice, J. R.

& Cocco, M. Frictional response induced by time-dependent fluctuations of the normal loading. _J. Geophys. Res. Solid Earth_ 106, 13455–13472 (2001). Article  Google Scholar  * Häring,

M. O., Schanz, U., Ladner, F. & Dyer, B. C. Characterisation of the Basel 1 enhanced geothermal system. _Geothermics_ 37, 469–495 (2008). Article  Google Scholar  Download references

ACKNOWLEDGEMENTS M.A. was supported by a graduate fellowship from Saudi Aramco. R.J. acknowledges funding from ExxonMobil through its membership in the MIT Energy Initiative. AUTHOR

INFORMATION AUTHORS AND AFFILIATIONS * Massachusetts Institute of Technology, 77 Massachusetts Ave, Cambridge, MA, 02139, USA Maryam Alghannam & Ruben Juanes Authors * Maryam Alghannam

View author publications You can also search for this author inPubMed Google Scholar * Ruben Juanes View author publications You can also search for this author inPubMed Google Scholar

CONTRIBUTIONS R.J. designed research; M.A. performed research; M.A. and R.J. analyzed results; and M.A. and R.J. wrote the paper. CORRESPONDING AUTHOR Correspondence to Ruben Juanes. ETHICS

DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PEER REVIEW INFORMATION _Nature Communications_ thanks Matthew Weingarten and the other,

anonymous, reviewer(s) for their contribution to the peer review of this work. Peer review reports are available. PUBLISHER’S NOTE Springer Nature remains neutral with regard to

jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION PEER REVIEW FILE RIGHTS AND PERMISSIONS OPEN ACCESS This article

is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give

appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in

this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative

Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a

copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Alghannam, M., Juanes, R. Understanding rate effects in

injection-induced earthquakes. _Nat Commun_ 11, 3053 (2020). https://doi.org/10.1038/s41467-020-16860-y Download citation * Received: 23 September 2019 * Accepted: 20 May 2020 * Published:

16 June 2020 * DOI: https://doi.org/10.1038/s41467-020-16860-y SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a

shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative