Metamaterial-enabled arbitrary on-chip spatial mode manipulation

ABSTRACT On-chip spatial mode operation, represented as mode-division multiplexing (MDM), can support high-capacity data communications and promise superior performance in various systems

and numerous applications from optical sensing to nonlinear and quantum optics. However, the scalability of state-of-the-art mode manipulation techniques is significantly hindered not only

by the particular mode-order-oriented design strategy but also by the inherent limitations of possibly achievable mode orders. Recently, metamaterials capable of providing

subwavelength-scale control of optical wavefronts have emerged as an attractive alternative to manipulate guided modes with compact footprints and broadband functionalities. Herein, we

propose a universal yet efficient design framework based on the topological metamaterial building block (BB), enabling the excitation of arbitrary high-order spatial modes in silicon

waveguides. By simply programming the layout of multiple fully etched dielectric metamaterial perturbations with predefined mathematical formulas, arbitrary high-order mode conversion and

mode exchange can be simultaneously realized with uniform and competitive performance. The extraordinary scalability of the metamaterial BB frame is experimentally benchmarked by a record

high-order mode operator up to the twentieth. As a proof of conceptual application, an 8-mode MDM data transmission of 28-GBaud 16-QAM optical signals is also verified with an aggregate data

rate of 813 Gb/s (7% FEC). This user-friendly metamaterial BB concept marks a quintessential breakthrough for comprehensive manipulation of spatial light on-chip by breaking the

long-standing shackles on the scalability, which may open up fascinating opportunities for complex photonic functionalities previously inaccessible. SIMILAR CONTENT BEING VIEWED BY OTHERS

EDGE-GUIDED INVERSE DESIGN OF DIGITAL METAMATERIAL-BASED MODE MULTIPLEXERS FOR HIGH-CAPACITY MULTI-DIMENSIONAL OPTICAL INTERCONNECT Article Open access 10 March 2025 ON-CHIP SILICON PHOTONIC

CONTROLLABLE 2 × 2 FOUR-MODE WAVEGUIDE SWITCH Article Open access 13 January 2021 VERSATILE PHOTONIC MOLECULE SWITCH IN MULTIMODE MICRORESONATORS Article Open access 20 February 2024

INTRODUCTION The internet data traffic has increased by more than a thousandfold in the last 20 years. Spatial-division multiplexing (SDM), employing different spatial orthogonal modes, has

been widely explored to tackle the upcoming forecasted “capacity crunch” in optical fiber communications1,2. Ultra-high-capacity data transmission has been demonstrated using single-mode

multicore fibers (MCFs)3, multimode fibers (MMFs)4 as well as their hybrid combination of few-mode multicore fibers (FM-MCFs)5. Besides, efficient mode multiplexing in free space has been

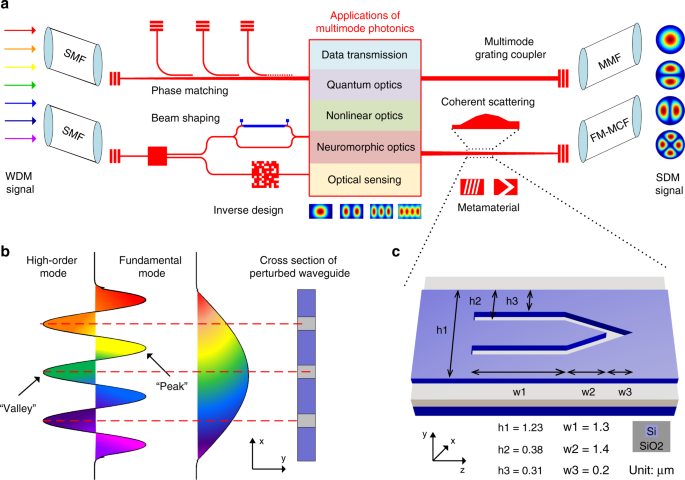
achieved with phase plates and multi-plane light conversion4. As illustrated in Fig. 1a, through introducing the spatial-mode-parallelism dimension to silicon photonic integrated circuits

(PICs), mode-division multiplexing (MDM) can significantly scale the bandwidth density of on-chip interconnects6,7, and also has great potential in MMF communications where the MMF is

excited directly by the multimode waveguide via a multimode grating coupler8. Moreover, mode-selective manipulation has greatly promoted the development of diverse information processing

fields ranging from performance-enhanced optical sensing9,10, neuro-inspired photonic computing11, to novel nonlinear12, and quantum optics devices13,14. For instance, the coupling of

spatial modes with other degrees of freedom (polarization, time, frequency, etc.) allows one to encode and process quantum information in higher dimensions, thus giving rise to more

efficient logic gates and noise resilient communications13,14. Besides, a neuro-inspired photonic reservoir for high-speed chaotic time series prediction has been realized by utilizing the

complex interference between multiple guided modes11. Moreover, the phase-matching condition for four-wave mixing can be satisfied in the visible regime through the dispersion engineering of

high-order waveguide modes, which opens an interesting wavelength window for nonlinear applications15. The essential foundation of multimode silicon photonics is on-chip spatial mode

manipulation, which has attracted tremendous research efforts over the past decade. Traditional techniques schematically shown in Fig. 1a, i.e., phase matching16,17, beam shaping18,19, and

coherent scattering20,21, all exhibit compromised performance in terms of excess losses (ELs), modal crosstalk (CT), fabrication tolerance, and device footprints. More specifically, although

extensive mode (de)multiplexers have been implemented with cascaded asymmetric directional couplers (ADCs)16 as well as subwavelength grating couplers (SWGs)17, the phase-matching condition

can hardly be satisfied and becomes extremely sensitive to fabrication imperfections for high-order modes, due to the large contrast in dispersion slopes between the bus waveguide and the

access waveguide. While the beam shaping method generally needs complicated designs of mode splitting, phase shifting, and mode combining18,19. Moreover, long optical paths are required to

introduce a phase difference of π between adjacent branches. As for the coherent scattering approach, the widely used inverse design method has enabled efficient mode conversion within

ultra-compact footprints22,23 by exploring the full design parameter space of photonic devices with arbitrary topologies24. However, the performance is heavily dependent on the numerical

optimization algorithms. Besides, the generated irregular nanostructures inevitably demand high fabrication accuracy owing to the tiny feature size. Metamaterials, consisting of optical

antenna arrays on the subwavelength scale, can provide advanced control of the optical wavefronts in both free space and integrated waveguides, leading to numerous applications from

high-efficiency holograms, ultrathin cloaks, to analog mathematical computing, nonlinear and topological photonics25,26,27. More recently, metamaterials have been introduced to silicon PICs

as a competitive alternative to control the light propagation on chip, and are particularly attractive in two aspects. On the one hand, metamaterials are capable of scattering guided modes

to new wavevectors within a propagation distance of only several times the wavelength, thus significantly reducing the device footprints28. Meanwhile, broadband mode manipulation can be

guaranteed due to an inverse relation between the device dimension and working bandwidth29. Previously, a diversity of mode converters with impressive performance have been reported by

imposing partially or fully etched nanostructures on metamaterial waveguides30,31,32,33. However, mode manipulation up to the fifth order still remains unachievable. It should be noted that

the abovementioned techniques all face fundamental limitations on scalability. First, these approaches are typically specific mode-order-oriented, which means each single-mode operator

requires a pre-determined structure selection based on analytic theory and intuition, followed by considerable iterations to optimize geometrical parameters, thus inevitably leading to a

long development time and huge trial-and-error costs. Second, arbitrary high-order mode manipulation is inherently not supported, restricted by either the working principle itself, e.g., the

coherent scatting approach, or the available fabrication technologies, e.g., the phase-matching method. Consequently, mode converters reported so far have mainly been constrained to

low-order mode cases. To this end, we develop a universal, simple yet efficient design framework to implement arbitrary on-chip mode conversion and mode exchange simultaneously, based on the

novel topological metamaterial building block (BB) concept. Dielectric perturbations are rationally engineered on metamaterial waveguides to realize the straightforward beam shaping

principle, which induce strong energy coupling between guided modes of interest within an ultra-compact conversion region. Our general strategy features a user-friendly

specification-oriented design, whereby the user simply defines the desired order of mode manipulation, and arbitrary even-order and odd-order mode operators can be directly determined by

programming the topological arrangement of multiple primitive TE0-TE2 BBs with predefined mathematical formulas. As such, uniform good performance with the ELs below 1.5 dB and the CT lower

than −8 dB (−12.5 dB assisted with a taper) from 1500 to 1600 nm has been achieved for arbitrary high-order mode operators in numerical simulations, which is further validated by sufficient

experimental results. To benchmark the extraordinary scalability of the metamaterial BB frame, we have experimentally implemented record high-order mode manipulation up to the twentieth in

silicon nanophotonics, to the best of our knowledge. As a proof-of-concept demonstration of the possible multimode applications for the metamaterial BB framework, high-speed data

transmission of 8-channel 16-quadrature amplitude modulation (16-QAM) signals is successfully verified at a symbol rate of 28 gigabauds (GBaud) and an aggregate data rate of 813 Gb/s with

bit error rates (BERs) under the 7% forward error correction (FEC) threshold of 3.8 × 10−3. RESULTS WORKING PRINCIPLE AND METAMATERIAL BUILDING BLOCK The propagation of electromagnetic waves

in a perturbed metamaterial waveguide can be approximately described by the classical coupled-mode theory (CMT)34,35. Assuming that guided modes propagate along the z direction, the

electric field distribution can be represented by a superposition of all the supported eigenmodes: $$E\left( {x,y,z} \right) = \mathop {\sum}\nolimits_m {A_m(z)\psi _m(x,y)e^{ - j\beta

_mz}}$$ (1) where _m_ is the mode subscript, _A__m_(_z_) is the amplitude, _β__m_ is the propagation constant, and _ψ__m_(_x,y_) is the electric mode profile of the _m_th-order eigenmode,

respectively. Due to the mode coupling, _A__m_(_z_) is dependent on the propagation distance and can be derived from the CMT equations: $$\frac{d}{{dz}}A_m(z) = - j\mathop {\sum}\nolimits_n

{\kappa _{mn}(z)A_n(z)e^{ - j(\beta _n - \beta _m)z}}$$ (2) where _κ__mn_ is the coupling coefficient between the _m_th-order mode and the _n_th-order mode, and defined as: $$\kappa

_{mn}\left( z \right) = \frac{\omega }{4}{\int\!\!\!\!\!\int} {\psi _m^ \ast (x,y){{\Delta }}\varepsilon (x,y,z)\psi _n(x,y)dxdy}$$ (3) where * denotes the complex conjugate, Δ_ε_(_x,y,z_)

is the refractive index perturbation. To realize efficient on-chip mode conversion, metamaterial waveguides should provide the necessary momentum compensation for the wavevector matching

between guided modes of interest. Besides, the spatial distribution of Δ_ε_(_x,y,z_) needs to be carefully engineered to maximize the “field overlap” integral

\({\int\!\!\!\!\!\int}{\int\!\!\!\!\!\int} {\psi _m^ \ast (x,y){{\Delta }}\varepsilon (x,y,z)\psi _n(x,y)dxdy}\) in Eq. (3) coupling coefficient. Therefore, dielectric perturbations are

commonly introduced to the regions where “peaks” or “valleys” are located in the transverse field profile of the high-order mode, as shown in Fig. 1b. In former studies, metamaterial mode

converters have been obtained by periodically varying the refractive index distribution along the propagation direction31,35,36; however, there exists a huge gap for the effective medium

theory mapping37 between the ideal index profile and the physical dielectric structure, constrained especially by the fabrication requirements. Besides, mode manipulation has also been

realized by modifying the supermode field profiles of SWG metamaterial waveguides30, which suffers the time-consuming mode-order-oriented optimization process. Previously, we have

demonstrated that a single dielectric slot can function as a power splitter and a phase shifter simultaneously33, which inspires the implementation of beam shaping principle completely with

metamaterial BBs consisting of fully etched dielectric slots (more information about the origin of metamaterial BBs is provided in Supplementary Note 1). Considering the symmetry property of

electric field profiles of eigenmodes, the TE0-TE2 metamaterial BB38 is designed with a symmetric arrow-like shape, as depicted in Fig. 1c. The two straight arms help to separate the

multimode waveguide into three single-mode channels and well confine the electric field to each field “peak”, while the followed V-shaped groove induces proper phase differences between the

three quasi-TE0 beams and combines them into the desired output mode. In this way, strong energy coupling between involved modes is obtained within an ultra-compact footprint of 1.23 × 2.7 

μm2. Moreover, the processes of mode splitting, phase shifting, and mode combining are independent and reciprocal on the input mode. As a result, the metamaterial BB inherently supports the

functionalities of both mode conversion and mode exchange, which has not been reported in most existent literature (a performance comparison of on-chip mode converters is provided in

Supplementary Note 6). Figure 2a, b presents the simulated mode evolution processes and coupling coefficients for the TE0-to-TE2 and TE2-to-TE0 mode conversion, respectively. It can be seen

that the input mode is gradually converted to the target output mode within a short propagation distance of only 2.7 μm (from 0.15 to 2.85 μm), and the calculated mode purity with the CMT

model matches well with the 3D finite-difference time-domain (3D-FDTD) simulation results. Besides, the coupling coefficient, which is roughly analog to a sinusoidal function, experiences a

transition from negative to positive values, thus ensuring the entire constructive contribution to the desired conversion35. To experimentally verify the TE0-TE2 metamaterial BB, we have

fabricated a silicon PIC consisting of a mode multiplexer with three input ports I0–I2, a TE0-TE2 mode operator, and a mode demultiplexer with three output ports O0–O2, as shown in Fig. 2c.

An extra PIC composed of two back-to-back (B2B) mode (de)multiplexers is also fabricated on the same chip to normalize the transmission spectra of the device. The designs of mode

(de)multiplexers are based on traditional ADCs structures. Figure 2d shows the scanning electron microscope (SEM) image of a TE0-TE2 metamaterial BB. Both the simulated and measured mode

manipulation efficiency are shown in Fig. 2e, f for comparison. In simulations, the ELs are below 1.3 dB and the CT is lower than −15 dB from 1510 to 1590 nm in both scenarios. It should be

noted that the crosstalk from the TE1 mode is extremely low (<−25 dB) and not shown in both plots. The measured ELs for the TE0-to-TE2 mode conversion are below 0.74 dB with the CT lower

than −12.75 dB in the wavelength range of 1510–1590 nm. For the TE2-to-TE0 mode conversion, the measured ELs are below 1.4 dB with the CT lower than −13.98 dB within the same wavelength

band. Especially, in the wavelength range of 1520–1580 nm, the measured ELs are lower than 1.4 dB and the CT is below −15 dB for both input mode cases. Overall, the experimental results

agree well with the simulation results. ARBITRARY HIGH-ORDER MODE OPERATOR The beam shaping principle provides a straightforward route to control arbitrary high-order modes; however, its

great potential has been significantly constrained by the complicated designs based on the traditional Mach–Zehnder interferometer architecture. Here we propose, for the first time, a

practicable universal implementation scheme by programming multiple metamaterial BBs in a simple parallel layout. Taking into consideration the symmetry property of electric field

distributions of eigenmodes, the even-order and odd-order mode operators are addressed separately. We first detail the metamaterial implementations of even-order mode operators. As shown in

Fig. 3a, there exists _N_/2+1 in-phase “peaks” and _N_/2 anti-phase “valleys” in the transverse electric field profile of the TE_N_ mode (_N_ is an even number). To realize the TE0-TE_N_

mode manipulation with the beam shaping technique, _N_/2 metamaterial BBs, containing _N_ dielectric slots in total, are needed to divide the multimode waveguide into _N_+1 single-mode

channels. Besides, in order to maximize the coupling coefficient between the two involved modes, the metamaterial BBs are engineered to exactly point at the positions of field “valleys” (the

implementation scheme of placing the metamaterial BBs at the field “peaks” is discussed in Supplementary Note 3). The symmetric geometry of the even-order mode operator is now determined by

only two parameters, i.e., the central distance between adjacent metamaterial BBs _w__d_ and the waveguide width _w_even. For simplicity, _w__d_ is assumed to be constant and _w_even is

expressed with a uniform formula: $$w_{{\rm{even}}} = w_d\frac{N}{2} + 2w_{{\rm{extra}}}$$ (4) where _w_extra is an extra waveguide width applied on both sides to better confine the mode

field. The optimized results from 3D-FDTD simulations are _w__d_ = 0.92 μm and _w_extra = 0.19 μm, respectively. For the implementation of the TE0-TE_N_ odd-order mode operator, there is

only one possible layout arrangement of metamaterial BBs, given the fact that the electric mode profile of the TE_N_ mode possesses central symmetry with the same number of field “peaks” and

“valleys”. As shown in Fig. 3b, (_N_ + 1)/2 metamaterial BBs are engineered to point at the (_N_ + 1)/2 field “peaks” of the TE_N_ mode, and the metamaterial BB closest to the waveguide

edge partially extends beyond the original waveguide region, as indicated by the “incomplete BB”. From the perspective of geometry structure, it is natural and reasonable to consider that

the TE0-TE_N_ odd-order mode operator can be obtained by directly truncating the TE0-TE_N_+1 even-odd mode operator with a fixed width _w_offset. As a result, the waveguide width _w_odd can

be determined by: $$w_{{\rm{odd}}} = {{d}}\frac{{N + 1}}{2} + 2w_{{\rm{extra}}} - w_{{\rm{offset}}}$$ (5) where _w_offset is the width of the truncated part, and the optimized value is 0.46 

μm. We quantitatively evaluate the mode manipulation efficiency of the universal metamaterial mode operators, and the simulated ELs and CT across a broad wavelength range from 1500 to 1600 

nm are summarized in Fig. 3c, d, respectively. As the mode order increases, both the ELs and CT first increase and eventually converge to a small oscillation range. Explicitly, the

metamaterial mode operator shares uniform performance with the ELs lower than 1.5 dB and CT below −8 dB over a 100 nm wavelength span. Besides, the major contribution of CT comes from the

related TE0, TE2, TE_N_–2, and TE_N_ mode, which can be largely attributed to their similar electric mode profiles of the same symmetry. It should be noted that the simple mathematically

defined layout arrangement of metamaterial BBs is intended to offer an initial design prototype for arbitrary high-order mode manipulation, and the conversion efficiency can be remarkably

enhanced by further optimizing the geometrical parameters for a specific mode. For example, the CT value of the TE0-to-TE_N_ mode conversion can be improved from −8 to −12.5 dB by adding a

properly designed taper (see Supplementary Note 8). Moreover, the device footprint of the metamaterial mode operator is only linearly dependent on the mode order with a constant length of

2.7 μm, hence making it possible for high integration density. Furthermore, it also features excellent thermal stability and good fabrication tolerance to the perturbation width variation of

±15 nm (see Supplementary Note 4). We have fabricated a series of high-order mode operators to experimentally verify the metamaterial BB concept. Mode (de)multiplexers consisting of

cascaded ADCs and SWGs are utilized to characterize the performance of devices. Figure 4a, b presents the SEM images of fabricated TE0-TE5 and TE0-TE10 mode operators and their measured mode

manipulation efficiency, respectively (more experimental results are provided in Supplementary Note 5). In the wavelength range from 1520 to 1580 nm, the TE0-TE5 mode operator can convert

the TE0 input mode into the TE5 output mode with the ELs lower than 3 dB and CT below −7.2 dB, and the major crosstalk is original from the TE3 mode. Meanwhile, it can also convert the TE5

input mode into the TE0 output mode with the ELs lower than 1.7 dB and CT below −8.3 dB. Moreover, the TE0-TE10 mode operator exhibits similar performance with the ELs lower than 3.8 dB and

CT below −7 dB across the wavelength band from 1540 to 1570 nm in both input cases. In general, the measured results are comparable to the numerical simulations. The mode-by-mode

characterization successfully validates the high-order mode manipulation capacity of the proposed metamaterial BBs. It should be noted that the performance degradation suffered by high-order

mode (de)multiplexers actually poses the greatest challenge during the whole performance assessment process. Although record high-order mode (de)multiplexer has been experimentally

demonstrated up to the 15th39, the critical phase-matching condition can hardly be well satisfied for all mode channels simultaneously owing to fabrication imperfections. In order to

validate the extraordinary scalability of the BBs-based design framework, we characterize the performance of high-order mode manipulation (>15th) by directly measuring the total ELs of 2,

6, and 10 cascaded B2B mode operators, which has already been verified to be a useful and effective method30,40. As shown in Fig. 4c, the designed PIC consists of a taper-based mode spot

size converter, multiple cascaded B2B mode operators, and a taper-based high-order mode filter. The TE0 input mode from the single-mode waveguide first gradually evolves into the fundamental

mode of the multimode waveguide, then repeatedly experiences the mode conversion process of TE0-to-TE_n_ and TE_n_-to-TE0 several times, as explained in Fig. 4d, e, and finally transmits

through the mode filter with almost no loss. Since the high-order modes generated in the conversion region are all filtered out, the total ELs measured at the output port directly represent

the mode manipulation efficiency. The measured transmission spectra for 6 cascaded B2B TE0-TE19 and TE0-TE20 mode operators are presented in Fig. 4f, g, respectively (More information is

provided in Supplementary Note 5). It should be noted that the cascaded configuration of mode operators forms a Fabry–Perot-like cavity, resulting in periodic resonances in the transmission

spectra. It is clear that the general trends of experimental results agree with the simulation results, particularly for the positions and shapes of resonance dips. Due to the accumulation

of fabrication errors, the measured total ELs increase almost linearly with the device number, as shown in Fig. 4h. The average ELs for the TE0-TE19 and TE0-TE20 mode conversion are

estimated to be ~0.53 and ~0.63 dB, respectively. HIGH-SPEED DATA COMMUNICATION We take the high-speed data transmission scenario as a proof-of-principle application of the

metamaterial-assisted universal multimode manipulation. An 8-channel BBs-based MDM circuit is fabricated on a silicon-on-insulator (SOI) wafer, as shown in Fig. 5a. The device consists of a

mode multiplexer with eight input ports (marked in red), a multimode waveguide of 60 μm, and a mode demultiplexer with eight output ports (marked in blue). Except for the TE1 mode directly

multiplexed with a TE0-TE1 ADC, the other six high-order modes are obtained with two-stage mode conversion. As illustrated in Fig. 5b, the input TE0 mode will first be converted to a middle

high-order mode through a metamaterial mode operator, which is then coupled into the final desired mode of the bus waveguide with a carefully designed TE_N_-to-TE_N_+1 ADC. To characterize

the MDM chip, the summed crosstalk from the other seven channels is measured for each output port. As shown in Fig. 5c, the CT ranges from −7.6 to −26.2 dB at 1540 nm for all mode channels.

Then, we successfully demonstrate the high-speed data transmission of 28-GBaud 16-QAM optical signals via the 8-channel MDM circuit. The experimental setup is shown in Fig. 5d and described

in detail in the method part. The calculated BERs for eight modes are shown in Fig. 5e, with all below the 7% FEC limit of 3.8 × 10−3. Besides, the corresponding recovered constellation

diagrams are also presented in Fig. 5f, which indicates a good signal quality for all eight channels, and the on-chip data transmission aggregate data rate is measured to be 813 Gb/s.

Following the same development path of SDM fiber communications, the key technology to enhance the channel capacity of on-chip MDM optical interconnects is to manipulate as many waveguide

modes as possible. For example, experimental results have shown an increasing single wavelength net capacity of 192 Gb/s, 1.23 Tb/s, and 1.51 Tb/s in MDM transmission of 3-mode PAM-4

signals41, 11-mode 16-QAM signals42, and 16-mode 16-QAM signals39, respectively. The metamaterial BBs make it possible to efficiently manipulate record high-order modes in practice, thus

significantly boosting the transmission capacity and bandwidth efficiency of on-chip optical links. Moreover, once the multimode fiber-to-chip coupling techniques are improved in the future,

the metamaterial-enabled arbitrary mode manipulation can play an important role in further combining the application scenarios of long-distance information transmission and on-chip data

transmission together. It is worth mentioning that all necessary components for coherent communications have been demonstrated on integrated platforms, including narrow-linewidth laser

sources43, high-speed in-phase/quadrature modulators (IQM)44, and high-speed photodetectors45. Besides, integrated coherent receiver46 and transmitters47 have also been experimentally

reported. Therefore, it is promising to obtain fully integrated MDM communication systems of ultra-high spectral efficiency. DISCUSSION In conclusion, we have proposed a universal

metamaterial-assisted BB framework to manipulate arbitrary on-chip spatial modes. The mathematically predefined topological arrangement of high-order mode operators allows user-friendly

specification-oriented design process. As such, uniform good performance of low ELs, low CT, and broad bandwidth has been achieved in both simulations and experiments. Besides, record

high-order mode manipulation up to the twentieth has been experimentally demonstrated to benchmark the excellent scalability of the metamaterial BBs. Furthermore, high-speed on-chip

8-channel MDM data transmission has been successfully verified with an aggregate data rate of 813 Gb/s (7% FEC). It is worth mentioning that the metamaterial BBs-based designs also feature

compact footprints, eased fabrication process, and good fabrication tolerance. The presented generic mode manipulation approach represents critical progress towards advanced control of more

physical dimensions of optic carriers, and the concept itself can be flexibly transferred to other waveguide platforms (InP, Si3N4, etc.) as well as other wavelength bands (O band,

mid-infrared band, etc.). The fundamentals gained from our on-chip arbitrary spatial mode manipulation may provide inspiration for more versatile metamaterial-assisted BB designs and could

promise a great breakthrough to boost the development of integrated quantum photonics, nonlinear photonics, and optical sensing. MATERIALS AND METHODS DEVICE SIMULATION In the numerical

simulations of CMT model, the transverse electric mode profiles of eigenmodes are obtained with the effective index method48, and the refractive index distribution of metamaterial structures

is generated manually with _n__Si_ = 3.476 and \(n_{{\rm{SiO}}_2} = 1.444\). For the 3D-FDTD simulations (FDTD solutions, Lumerical), we define the metamaterial structures directly with the

default material database, which has considered the material dispersion. And the simulation time is set to be 3000 fs, within which the auto-shutoff criteria can be satisfied. Besides, the

discretization grid is automatically generated with a mesh accuracy index of 4, which provides a good tradeoff between accuracy, memory requirements and simulation time. Other settings

remain the default values. Besides, the ELs and CT are defined as \({\rm{ELs}} = - 10{\rm{log}}_{10}\frac{{P_{{\rm{desired}}}}}{{P_{{\rm{input}}}}}\) and \({{{\mathrm{CT}}}} =

{{{\mathrm{max}}}}\{ 10{\rm{log}}_{10}\frac{{P_{{\rm{other}}}}}{{P_{{\rm{desired}}}}}\}\), where _P_input, _P_desired, and _P_other are the power of the input mode, the desired output mode,

and the other interfering mode, respectively. DEVICE FABRICATION The devices are fabricated on an SOI wafer with a 220 nm top silicon layer on a 3 μm silicon dioxide layer. The designed

patterns are first defined by the electron beam lithography system and then fully etched by using a single-step inductively coupled plasma dry etching. A 1-μm-thick silicon dioxide

protection layer is deposited on top of the devices by plasma-enhanced chemical vapor deposition. MEASUREMENT SETUP Grating couplers are used to interface the silicon waveguides and the

single-mode fibers, with the coupling loss optimized to be 6.5 dB per facet. The input light from a continuous-wave tunable laser source (Keysight 81960A) is directly launched onto the chip

after being polarized by a polarization controller, and the output light is monitored by an optical power meter (Keysight N7744A). For the mode-by-mode characterization of low-order

TE0-TE_n_ (_n_ ≤ 10) mode operator, the fabricated PIC consists of a mode multiplexer with input ports I0−I_n_, a mode operator, and a mode demultiplexer with output ports O0–O_n_. The

injected TE0 mode from the input port _I__j_(_j_ = 0 and _n_) is first multiplexed to the TE_j_ mode (_j_ = 0 and _n_) in the multimode bus waveguide, and then transmits through the

metamaterial mode operator. After mode conversion, all modes are demultiplexed to the TE0 mode and exit the corresponding output port _O__k_(_k_ = 0, 1,…, _n_). The mode transmission from

the TE_j_ mode (_j_ = 0 and _n_) to the TE_k_ mode (_k_ = 0, 1,…, _n_) is finally obtained after normalization with respect to the transmission of the reference circuit. HIGH-SPEED DATA

COMMUNICATION OF 28-GBAUD 16-QAM SIGNAL Multimode silicon photonics has offered new opportunities for extensive research fields ranging from quantum photonics, topological photonics as well

as nonlinear photonics. Here, we take the high-speed data transmission scenario as a proof-of-principle application of the metamaterial-assisted universal multimode manipulation. The

experimental setup is given in Fig. 5d. The output wavelength of the tunable laser is set to be 1540 nm to match the peak wavelength of the grating coupler. A 28-GBaud 16-QAM signal is

generated by the digital-analog converter with a sample rate of 64 GSa/s, and boosted by electronic amplifiers to drive the 22-GHz IQM. The modulated optical signal is then amplified and

time gated by an acousto-optic modulator with a duty cycle of 12.5%. To emulate eight WDM channels with a spacing of 50 GHz, a spectrally shaped amplified spontaneous emission noise is

generated and then combined with the time-gated signal. The obtained WDM signal is amplified and split into eight individual components, which suffer different time delays for signal

decorrelation before being injected into the MDM circuit. At the receiver side, the local oscillator is gated and delayed in a similar manner. Meanwhile, polarization multiplexing and

time-division multiplexing technology are utilized before the output signals detected by a polarization-diverse coherent receiver. The received electric signals are sent into a real-time

oscilloscope to recover the 16-QAM data, where a multiple-in-multiple-output–based digital signal processing algorithm is adopted to mitigate the inter-CT. REFERENCES * Richardson, D. J.,

Fini, J. M. & Nelson, L. E. Space-division multiplexing in optical fibres. _Nat. Photonics_ 7, 354–362, https://doi.org/10.1038/nphoton.2013.94 (2013). Article  ADS  Google Scholar  *

Puttnam, B. J., Rademacher, G. & Luís, R. S. Space-division multiplexing for optical fiber communications. _Optica_ 8, 1186–1203, https://doi.org/10.1364/OPTICA.427631 (2021). Article 

ADS  Google Scholar  * Hayashi, T. et al. Design and fabrication of ultra-low crosstalk and low-loss multi-core fiber. _Opt. Express_ 19, 16576–16592 (2011). Article  ADS  Google Scholar  *

Rademacher, G. et al. Peta-bit-per-second optical communications system using a standard cladding diameter 15-mode fiber. _Nat. Commun._ 12, 4238, https://doi.org/10.1038/s41467-021-24409-w

(2021). Article  ADS  Google Scholar  * Van Uden, R. G. H. et al. Ultra-high-density spatial division multiplexing with a few-mode multicore fibre. _Nat. Photonics_ 8, 865–870,

https://doi.org/10.1038/nphoton.2014.243 (2014). Article  ADS  Google Scholar  * Luo, L. W. et al. WDM-compatible mode-division multiplexing on a silicon chip. _Nat. Commun._ 5, 3069,

https://doi.org/10.1038/ncomms4069 (2014). Article  ADS  Google Scholar  * Liu, Y. J. et al. Arbitrarily routed mode-division multiplexed photonic circuits for dense integration. _Nat.

Commun._ 10, 3263, https://doi.org/10.1038/s41467-019-11196-8 (2019). Article  ADS  Google Scholar  * Tong, Y. Y. et al. Efficient mode multiplexer for few-mode fibers using integrated

silicon-on-insulator waveguide grating coupler. _IEEE J. Quantum Electron._ 56, 8400107, https://doi.org/10.1109/JQE.2019.2950126 (2020). Article  Google Scholar  * Hoppe, N. et al. Design

of an integrated dual-mode interferometer on 250 nm silicon-on-insulator. _IEEE J. Sel. Top. Quantum Electron._ 23, 8200508 (2017). Article  Google Scholar  * Hadibrata, W. et al. Compact,

high-resolution inverse-designed on-chip spectrometer based on tailored disorder modes. _Laser Photonics Rev._ 15, 2000556 (2021). Article  ADS  Google Scholar  * Sunada, S. & Uchida, A.

Photonic neural field on a silicon chip: large-scale, high-speed neuro-inspired computing and sensing. _Optica_ 8, 1388–1396, https://doi.org/10.1364/OPTICA.434918 (2021). Article  ADS 

Google Scholar  * Kittlaus, E. A., Otterstrom, N. T. & Rakich, P. T. On-chip inter-modal Brillouin scattering. _Nat. Commun._ 8, 15819, https://doi.org/10.1038/ncomms15819 (2017).

Article  ADS  Google Scholar  * Feng, L. T. et al. On-chip coherent conversion of photonic quantum entanglement between different degrees of freedom. _Nat. Commun._ 7, 11985,

https://doi.org/10.1038/ncomms11985 (2016). Article  ADS  Google Scholar  * Mohanty, A. et al. Quantum interference between transverse spatial waveguide modes. _Nat. Commun._ 8, 14010,

https://doi.org/10.1038/ncomms14010 (2017). Article  ADS  Google Scholar  * Zhao, Y. et al. Visible nonlinear photonics via high-order-mode dispersion engineering. _Optica_ 7, 135–141,

https://doi.org/10.1364/OPTICA.7.000135 (2020). Article  ADS  Google Scholar  * Dai, D. X. et al. 10-Channel mode (de)multiplexer with dual polarizations. _Laser Photonics Rev._ 12, 1700109

(2017). Article  ADS  Google Scholar  * He, Y. et al. Silicon high-order mode (De) multiplexer on single polarization. _J. Lightwave Technol._ 36, 5746–5753,

https://doi.org/10.1109/Jlt.2018.2878529 (2018). Article  ADS  Google Scholar  * Huang, Y. Y., Xu, G. Y. & Ho, S. T. An ultracompact optical mode order converter. _IEEE Photonics

Technol. Lett._ 18, 2281–2283, https://doi.org/10.1109/Lpt.2006.884886 (2006). Article  ADS  Google Scholar  * Park, J. B., Yeo, D. M. & Shin, S. Y. Variable optical mode generator in a

multimode waveguide. _IEEE Photonics Technol. Lett._ 18, 2084–2086, https://doi.org/10.1109/LPT.2006.883203 (2006). Article  ADS  Google Scholar  * Liu, V., Miller, D. A. B. & Fan, S. H.

Ultra-compact photonic crystal waveguide spatial mode converter and its connection to the optical diode effect. _Opt. Express_ 20, 28388–28397, https://doi.org/10.1364/OE.20.028388 (2012).

Article  ADS  Google Scholar  * Chen, D. G. et al. Low-loss and fabrication tolerant silicon mode-order converters based on novel compact tapers. _Opt. Express_ 23, 11152–11159,

https://doi.org/10.1364/OE.23.011152 (2015). Article  ADS  Google Scholar  * Jia, H. et al. Inverse-design and demonstration of ultracompact silicon meta-structure mode exchange device. _ACS

Photonics_ 5, 1833–1838, https://doi.org/10.1021/acsphotonics.8b00013 (2018). Article  Google Scholar  * Jia, H. et al. Ultra-compact dual-polarization silicon mode-order converter. _Opt.

Lett._ 44, 4179–4182, https://doi.org/10.1364/OL.44.004179 (2019). Article  ADS  Google Scholar  * Piggott, A. Y. et al. Inverse design and demonstration of a compact and broadband on-chip

wavelength demultiplexer. _Nat. Photonics_ 9, 374–377, https://doi.org/10.1038/nphoton.2015.69 (2015). Article  ADS  Google Scholar  * Staude, I. & Schilling, J. Metamaterial-inspired

silicon nanophotonics. _Nat. Photonics_ 11, 274–284, https://doi.org/10.1038/nphoton.2017.39 (2017). Article  ADS  Google Scholar  * Kildishev, A. V., Boltasseva, A. & Shalaev, V. M.

Planar photonics with metasurfaces. _Science_ 339, 1232009 (2013). Article  Google Scholar  * Jahani, S. & Jacob, Z. All-dielectric metamaterials. _Nat. Nanotechnol._ 11, 23–36,

https://doi.org/10.1038/nnano.2015.304 (2016). Article  ADS  Google Scholar  * Li, Z. Y. et al. Controlling propagation and coupling of waveguide modes using phase-gradient metasurfaces.

_Nat. Nanotechnol._ 12, 675–683 (2017). Article  ADS  Google Scholar  * Mansuripur, M. The uncertainty principle in classical optics. _Opt. Photonics N._ 13, 44–48 (2002). ADS  MATH  Google

Scholar  * Guo, J. S. et al. Ultra-compact and ultra-broadband guided-mode exchangers on silicon. _Laser Photonics Rev._ 14, 2000058, https://doi.org/10.1002/lpor.202000058 (2020). Article 

ADS  Google Scholar  * Ohana, D. et al. Dielectric metasurface as a platform for spatial mode conversion in nanoscale waveguides. _Nano Lett._ 16, 7956–7961,

https://doi.org/10.1021/acs.nanolett.6b04264 (2016). Article  ADS  Google Scholar  * Wang, H. W. et al. Compact silicon waveguide mode converter employing dielectric metasurface structure.

_Adv. Optical Mater._ 7, 1801191, https://doi.org/10.1002/adom.201801191 (2019). Article  Google Scholar  * Zhao, Y. T. et al. Ultra-compact silicon mode-order converters based on dielectric

slots. _Opt. Lett._ 45, 3797–3800, https://doi.org/10.1364/OL.391748 (2020). Article  ADS  Google Scholar  * Yariv, A. & Yeh, P. _Optical Waves in Crystals: Propagation and Control of

Laser Radiation._ (Wiley, Hoboken, 1983). Google Scholar  * Ohana, D. & Levy, U. Mode conversion based on dielectric metamaterial in silicon. _Opt. Express_ 22, 27617–27631,

https://doi.org/10.1364/OE.22.027617 (2014). Article  ADS  Google Scholar  * Greenberg, Y. & Karabchevsky, A. Spatial eigenmodes conversion with metasurfaces engraved in silicon ridge

waveguides. _Appl. Opt._ 58, F21–F25, https://doi.org/10.1364/AO.58.000F21 (2019). Article  Google Scholar  * Rytov, S. Electromagnetic properties of a finely stratified medium. _Sov. Phys.

JEPT_ 2, 466–475 (1956). MathSciNet  MATH  Google Scholar  * Xiang, J. L. et al. Scalable metasurface building blocks for arbitrary on-chip high-order mode manipulation. _2020 European

Conference on Optical Communications (ECOC)._ 1–4 (IEEE, Brussels, 2020). Google Scholar  * He, Y. et al. Record high-order mode-division-multiplexed transmission on chip using

gradient-duty-cycle subwavelength gratings. _Optical Fiber Communication Conference._ F3A.2 (OSA Technical Digest, Washington, 2021). Google Scholar  * Zhang, G. W. & Liboiron-Ladouceur,

O. Scalable and low crosstalk silicon mode exchanger for mode division multiplexing system enabled by inverse design. _IEEE Photonics J._ 13, 6601013,

https://doi.org/10.1109/JPHOT.2021.3061112 (2021). Article  Google Scholar  * Hsu, Y. et al. 2.6 Tbit/s on-chip optical interconnect supporting mode-division-multiplexing and PAM-4 signal.

_IEEE Photonics Technol. Lett._ 30, 1052–1055, https://doi.org/10.1109/LPT.2018.2829508 (2018). Article  ADS  Google Scholar  * Huang, H. Z. et al. Demonstration of terabit coherent on-chip

optical interconnects employing mode-division multiplexing. _Opt. Lett._ 46, 2292–2295, https://doi.org/10.1364/OL.424727 (2021). Article  ADS  Google Scholar  * Marin-Palomo, P. et al.

Microresonator-based solitons for massively parallel coherent optical communications. _Nature_ 546, 274–279, https://doi.org/10.1038/nature22387 (2017). Article  ADS  Google Scholar  * Xu,

M. Y. et al. High-performance coherent optical modulators based on thin-film lithium niobate platform. _Nat. Commun._ 11, 3911, https://doi.org/10.1038/s41467-020-17806-0 (2020). Article 

ADS  Google Scholar  * Lischke, S. et al. Ultra-fast germanium photodiode with 3-dB bandwidth of 265 GHz. _Nat. Photonics_ 15, 925–931, https://doi.org/10.1038/s41566-021-00893-w (2021).

Article  ADS  Google Scholar  * Wang, Y. L. et al. Ultrahigh-speed graphene-based optical coherent receiver. _Nat. Commun._ 12, 5076, https://doi.org/10.1038/s41467-021-25374-0 (2021).

Article  ADS  Google Scholar  * Dong, P. et al. Monolithic silicon photonic integrated circuits for compact 100+ Gb/s coherent optical receivers and transmitters. _IEEE J. Sel. Top. Quantum

Electron._ 20, 6100108, https://doi.org/10.1109/JSTQE.2013.2295181 (2014). Article  ADS  Google Scholar  * Abu-Elmaaty, B. E. et al. General silicon-on-insulator higher-order mode converter

based on substrip dielectric waveguides. _Appl. Opt._ 58, 1763–1771, https://doi.org/10.1364/AO.58.001763 (2019). Article  ADS  Google Scholar  Download references ACKNOWLEDGEMENTS The

authors thank H. K. Tsang for very fruitful discussions. This work was supported by National Key R&D Program of China (2019YFB2203101), Natural Science Foundation of China (NSFC)

(62175151 and 61835008), Natural Science Foundation of Shanghai (19ZR1475400), and Open Project Program of Wuhan National Laboratory for Optoelectronics (2018WNLOKF012). AUTHOR INFORMATION

AUTHORS AND AFFILIATIONS * State Key Laboratory of Advanced Optical Communication Systems and Networks, Department of Electronic Engineering, Shanghai Jiao Tong University, Shanghai,

200240, China Jinlong Xiang, Zhiyuan Tao, Xingfeng Li, Yaotian Zhao, Yu He, Xuhan Guo & Yikai Su Authors * Jinlong Xiang View author publications You can also search for this author

inPubMed Google Scholar * Zhiyuan Tao View author publications You can also search for this author inPubMed Google Scholar * Xingfeng Li View author publications You can also search for this

author inPubMed Google Scholar * Yaotian Zhao View author publications You can also search for this author inPubMed Google Scholar * Yu He View author publications You can also search for

this author inPubMed Google Scholar * Xuhan Guo View author publications You can also search for this author inPubMed Google Scholar * Yikai Su View author publications You can also search

for this author inPubMed Google Scholar CONTRIBUTIONS X.G., J.X., and Z.T. developed the concept and conceived the experiments. J.X. and Z.T. performed the theoretical and numerical

analyses. J.X. and Y.Z. fabricated and characterized the devices. J.X., X.L., and Y.H. carried out the transmission measurements and analyzed the results. X.G., J.X., and Y.S analyzed the

data and contributed to writing and finalizing the article. CORRESPONDING AUTHORS Correspondence to Xuhan Guo or Yikai Su. ETHICS DECLARATIONS CONFLICT OF INTEREST The authors declare no

competing interests. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION FOR METAMATERIAL ENABLED ARBITRARY ON-CHIP SPATIAL MODE MANIPULATION RIGHTS AND PERMISSIONS OPEN ACCESS This article

is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give

appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in

this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative

Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a

copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Xiang, J., Tao, Z., Li, X. _et al._

Metamaterial-enabled arbitrary on-chip spatial mode manipulation. _Light Sci Appl_ 11, 168 (2022). https://doi.org/10.1038/s41377-022-00859-9 Download citation * Received: 10 December 2021 *

Revised: 15 May 2022 * Accepted: 21 May 2022 * Published: 01 June 2022 * DOI: https://doi.org/10.1038/s41377-022-00859-9 SHARE THIS ARTICLE Anyone you share the following link with will be

able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing

initiative