The static structure of polyrotaxane in solution investigated by contrast variation small-angle neutron scattering

ABSTRACT Polyrotaxane (PR) possesses a supramolecular structure in which cyclic molecules are threaded into an axial polymer. In this study, the static structure of PR dissolved in a good

solvent was investigated using contrast variation small-angle neutron scattering. The conformation of the axial linear polymer and the alignment of cyclic molecules within the axial polymer

were evaluated quantitatively with the help of a detailed derivation of scattering theory. The decomposed partial scattering functions of the cyclic molecules and the axial polymer and the

cross-correlation between cyclic molecules and an axial polymer strongly supported the idea that the alignment of cyclic molecules threaded on the axial polymer is random. On the basis of

experimental observation, the entropic origin of the stiffening of PR due to the array of cyclic molecules is discussed. SIMILAR CONTENT BEING VIEWED BY OTHERS MOLECULAR DYNAMICS AND

STRUCTURE OF POLYROTAXANE IN SOLUTION Article 27 January 2021 ELECTRON-PHONON COUPLING AND VIBRATIONAL PROPERTIES OF SIZE-SELECTED LINEAR CARBON CHAINS BY RESONANCE RAMAN SCATTERING Article

Open access 27 August 2022 CHARACTERIZING BLOCK-COPOLYMER MICELLES USED IN NANOMEDICINES VIA SOLUTION STATIC SCATTERING TECHNIQUES Article Open access 31 May 2021 INTRODUCTION The

investigation of polymer solutions has long retained a fundamental place in the research of polymers.1 Because polymers cannot exist in a gaseous state, a simple experimental method for the

characterization of a single polymer chain must be performed with dilute polymer solutions, in which the polymer molecules are well separated. Theoretically, the mean-square end-to-end

distances, viscosity and dynamics of a single polymer chain have been intensively studied.2, 3 The first statistical mechanical approach for determining the configuration of a polymer in

solution was developed by Kuhn;4 Flory then introduced the excluded-volume effect for the description of real polymer chains in good solvents.5 Some time later, the theory for the dilute

solution behavior of flexible polymers was almost complete.1 However, the problems of stiff or semiflexible polymers still remained. These problems were solved by Yamakawa who proposed the

helical worm-like chain model to describe the equilibrium conformational and dynamic properties of all kinds of real polymers across a large breadth of length scales; that is, the theory can

bridge the gap between atomic-level models and continuum theories.3, 6 The field of supramolecular chemistry has developed rapidly in recent times.7 Supramolecular species are held together

and organize themselves by means of non-covalent binding interactions, such as intermolecular forces and electrostatic or hydrogen bonding. Polyrotaxane (PR), which is a topological

copolymer composed of cyclic molecules threaded into a linear polymer chain, is one of the most promising supramolecules.8 The cyclic molecules in PR are mechanically interlocked by capping

the axial chain with bulky end groups, and their degrees of freedom involve slide, rotation and transfer because of the diffusion of monomer units of the axial polymer. These unique kinetic

properties have been used for the development of novel functional materials.9 For example, slide-ring gel has been produced by chemically crosslinking several cyclic molecules on different

axial polymers.10 The properties of slide-ring gel are quite unique; for example, high extensibility, high swelling properties and high resistance to external stress.11 Unlike conventional

covalent macromolecules, the physical properties of PR have just begun to be studied and are not yet well understood. A few small-angle neutron scattering (SANS) investigations have been

conducted on dilute and semidilute solutions of PR.12, 13, 14, 15, 16 It has been found that the persistent length of PR is much longer than that of a flexible polymer with the same contour

length, and the conformation of PR is much affected by the inclusion ratio of the cyclic molecules13 and the concentration of PR itself.15, 16 Because PR possesses a binary-component

supramolecular structure, a direct observation of the individual structures and dynamics of the cyclic molecules and the axial polymer in PR has been difficult with conventional experimental

techniques. The aim of this study was to elucidate the detailed static structure of PR by means of contrast variation SANS (CV-SANS). Using neutrons as a probe, the contrast variation

technique can be feasible on the basis of hydrogen/deuterium replacement to tune the visibility of different components in the system. By applying CV-SANS, the measured scattering

intensities with different scattering contrasts can be decomposed into the partial scattering functions of each component, and detailed analyses of the partial scattering functions lead to

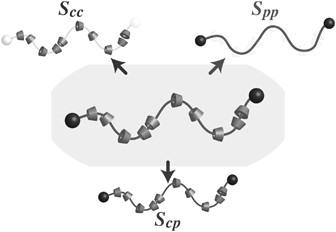
fine structural understanding of the components. Regarding the observable partial scattering function in PR, two self-correlation functions for cyclic molecules and an axial polymer, as well

as one cross-correlation function between cyclic molecules and the axial polymer, must be considered. In Figure 1, a schematic picture of the partial scattering functions of PR is depicted.

Before this paper, a short article was published to introduce this study briefly.17 In this paper, we first derive the form factor for cyclic molecules threaded into the axial polymer by

taking account of the one-dimensional distribution of cyclic molecules on the axis. At the same time, the form factor of the axial polymer and the cross-correlation between cyclic molecules

and the axis could be derived in a manner similar to the derivation of the form factor for cyclic molecules. The total evaluation of the partial scattering functions enables us to determine

the radius of gyration of the axial polymer and the one-dimensional array of the cyclic molecules in PR. SCATTERING THEORY In this section, the scattering functions for PR are derived. The

backbone of the scattering functions consists of two parts: the Kratky–Porod worm-like chain model18 obtained by Yamakawa and Yoshizaki,19 and the random copolymer model derived by Endo and

Shibayama.20 The worm-like chain model is a good model for very stiff polymers, where the correlation between the two bond vectors and decays exponentially as with the length of the bond

vector _l_ and the persistence length _l_p. This model should be applicable to semiflexible PR. The chain thickness of PR, which affects the scattering curve in a high-Q range, is

indispensable; however, it can be practically incorporated into the scattering function as described below. It is necessary to consider the three different scattering contributions

individually, namely, two self-correlations of the axial polymer and the beaded cyclic molecules and the cross-correlation between the axis and the beads. We will summarize the worm-like

chain model and the random copolymer model first, after which the scattering functions for the beads, the axis and the cross-correlation will be derived one by one. WORM-LIKE CHAIN MODEL The

worm-like chain model obtained by Yoshizaki _et al._19 is an empirical equation connecting the Debye function for a Gaussian chain at low _Q_ and the form factor of a rod at high _Q_ in

continuity; that is with the magnitude of the scattering vector _Q_ (=4π sin(_θ_/2)/_λ_; scattering angle _θ_, wavelength of incident beam _λ_), contour length _L_ and persistence length

_l_p. The static segment (Kuhn) length _b_ is related to the persistence length by _l_p=_b_/2. The Debye function _P_Debye(_Q_, _L_, _l_p) is defined as where _u_=_R_g2_Q_2, with the radius

of gyration of the linear polymer _R_g given by The form factor _P_Rod(_Q_, _L_) in Equation (2) is written as with the sine integral . The cross-over region between _P_Debye(_Q_, _L_, _l_p)

and _P_Rod(_Q_, _L_) in Equation (2) is corrected by functions _χ_(_Q_, _L_, _l_p) and _Γ_(_Q_, _L_, _l_p). The factor _χ_(_Q_, _L_, _l_p) is given by and _Γ_(_Q_, _L_, _l_p) is expressed

as a function of _Q_, _L_, _l_p and 35 coefficients calculated by Yoshizaki and Yamakawa.19 THE RANDOM COPOLYMER MODEL The random copolymer model of type A–B was derived by Endo _et al._ on

the basis of Gaussian statistics.20 In the case of a linear random copolymer with monomer-A and monomer-B, the partial scattering function of monomer-A is described by discretization of the

Debye function with interval _l_0 as where _N_ is the segment number (that is, _N_=_L_/_b_) and _n_0 is related to the interval _l_0 as _l_0=_N_/_n_0. In this definition, _l_0 × _l_p

corresponds to the length of a single monomer unit. _A__m/n_(_k_) is an _n_0-dimensional vector defined by for the _k_th interval. The ensemble average is with the length fraction of

monomer-A component _Φ_A. In the case of a purely random process for the distribution of monomers, _A__m_(_i_)·_A__n_(_j_) in Equation (7) can be substituted by ; then, an analytic form of

Equation (7) is obtained as with _x_=_Q_2_R_g2 and _N_=1+(1−_Φ_A)/(_Φ_A_n_0). PARTIAL SCATTERING FUNCTIONS FOR POLYROTAXANE The scattering intensity _I_(_Q_) of PR in solution is given by

where C and P indicate cyclic molecules and the axial polymer in PR, respectively. Δ_ρ__i_ (_i_=C, P) is the scattering contrast between component-_i_ and the solvent, that is,

Δ_ρ__i_=_ρ__i_–_ρ_S with the scattering length densities of component-_i_, _ρ__i_ and that of the solvent, _ρ_S. _S__ij_(_Q_) denotes the partial scattering function in PR, namely,

_S_CC(_Q_) and _S_PP(_Q_), which represent the intracorrelation of cyclic molecules and the axial polymer, respectively; _S_CP(_Q_) expresses the intercorrelation (or cross-correlation)

between cyclic molecules and the axial polymer. In Figure 1, a conceptual scheme of the partial scattering functions is illustrated. Derivation of each _S__ij_(_Q_) will be described below

without considering the intermolecular interaction. The partial scattering function of the axial polymer, _S_PP(_Q_), can be approximated by the worm-like chain model given by Equation (2):

where _n_PR is the number density of PR and _V_P is the volume of the axial polymer. For the description of the partial scattering function of cyclic molecules, _S_CC(_Q_), we need to

integrate the random copolymer model into the worm-like chain model. The unification can be carried out with substitution of Equation (7) for Equation (3); at the same time, the form factor

of a rod given by Equation (5) must be replaced by See Equations (A6) and (A7) in Appendix A. Finally, _S_CC(_Q_) is given by where _V_C is the total volume of the cyclic molecules threaded

on the single axial polymer. _χ_(_Q_, _L_, _l_p) and _Γ_(_Q_, _L_, _l_p) in Equation (14) are assumed to be identical to those given by Yoshizaki and Yamakawa.19 In the event that the cyclic

molecules distribute randomly on the axial polymer, the analytic forms given by Equations (10) and (A8) can be used. The intercorrelation between cyclic molecules and the axial polymer,

_S_CP(_Q_), can also be calculated with the worm-like chain model; that is, _S_CP(_Q_) can be described as where and with where _A__n_(_j_) defined by Equation (8) represents the probability

density of the axial polymer, that is, _A__n_(_j_)=1 for any _j_. Furthermore, by assuming that cyclic molecules can locate equally at any site in the axial polymer, we can replace

_A__m_(_i_) by its ensemble average . In this case, is obtained, where _P_CP(_Q_) can be simplified as DISTRIBUTION OF CYCLIC MOLECULES ON THE AXIAL POLYMER As discussed in the above

section, the partial scattering functions, _S_CC(_Q_) and _S_CP(_Q_), can reflect the row of cyclic molecules on the axial polymer. The distribution of cyclic molecules on the axial polymer

can be evaluated by quantitative analyses of _S_CC(_Q_) and _S_CP(_Q_) using Monte Carlo simulations. To investigate biased alignments of the cyclic molecules, we define the conditional

probability that two cyclic molecules are successively placed as _φ_cc and the conditional probability that two cyclic molecules are not successively placed as _φ_c. By defining the total

length fraction of the cyclic molecules as _Φ_c, we can relate _Φ_c to _φ_cc and _φ_c as follows: In the model, _Φ_c>_φ_cc indicates a repulsive interaction between cyclic molecules, and

Φc <_φ_cc indicates an attractive interaction between cyclic molecules. The Monte Carlo simulation for _S_CC(_Q_) can be performed by using Equations (8) and (14), where _A__m,n_(_k_) is

given by and where _φ__k_ is a generated random number between 0 and 1. In this simple model, however, the expected value for _A__m_(_i_) is constant, independently of _φ_cc and _φ_c. In

other words, the ensemble value <_A__m_(_i_)> is always constant for any values of _φ_cc and _φ_c so that _S_CP(_Q_) cannot be affected by the arrangement of the cyclic molecules.

Therefore, it is only possible to obtain information about the array of cyclic molecules by analyzing _S_CC(_Q_) with this method. INTERPOLYMER INTERACTION By condensing the concentration of

polymers in solution, the polymers gradually start to overlap each other above the overlap concentration _c_*. In the event that the concentration of the polymers is far below _c_*, the

static scattering intensities _I_(_Q_) can be described with the form factor _P_poly(_Q_): where _I_0 is the forward scattering intensity, which can be calculated as _I_0=_n_ × _V_2 × _Δρ_2

with the number density of the polymer _n_, the volume of the polymer _V_ and the scattering contrast between the polymer and the solvent _Δρ_. If the concentration of the polymer is in the

vicinity of _c_*, Equation (24) is invalid because of the effect of interpolymer interactions. The Zimm formula treats the interpolymer interaction with the second virial coefficient _A_2,

which is given by where _M_ is the molecular weight of the polymer, and _c_ is the mass-concentration of the solute. For polymer solutions, _A_2 can be related to the excluded volume _ν_ as

with Avogadro's number _N_A and the molar mass of the monomer, _m_. Equation (25) was originally derived with single contact approximation and an assumption that 2_A_2_Mc_ is very small

compared with unity;21 therefore, the applicable concentration should be rather diluted. In fact, the expression given by Equation (25) has been proved to be valid at much higher

concentrations theoretically,21 and we have also experimentally confirmed its validity in PR solutions.16 The Ornstein–Zernike (O-Z) formula is also typically applied for semidilute polymer

solutions, where _I_(_Q_) ∝ (1+_ξ_2_Q_2)−1 (with the correlation length _ξ_);22 however, it has been experimentally confirmed that the O-Z formula does not fit PR solutions well because of

the considerably large persistence length and thickness of PR.16 Therefore, Equation (25) will be combined with Equations (12), (14) and (19) to analyze the partial scattering functions

quantitatively. EXPERIMENTAL PROCEDURE MATERIALS In this study, PR was composed of poly(ethylene glycol) (PEG) as the axial polymer and α-cyclodextrin (αCD) as the cyclic molecule. To

execute contrast variation experiments, we synthesized two types of PRs, namely, h-PR consisting of hydrogenated poly(ethylene glycol) (h-PEG) and d-PR consisting of fully deuterated

poly(ethylene glycol) (d-PEG). Hydrogenated PEG was purchased from Fluka (Buchs, Switzerland), and the deuterated polymer was purchased from Cambridge Isotope Laboratories Inc (Andover, MA,

USA); their polydispersity indices were <1.2. αCD was purchased from Nihon Shokuhin Kako Co. Ltd (Tokyo, Japan) (αCD content >99%). The degree of polymerization of both hydrogenated

and deuterated PEG was 800, which corresponds to 3.5 × 104 g mol−1 with hydrogenated PEG conversion. PEG in PR was end-capped with adamantine to prevent the threaded αCDs from escaping. The

average number of αCDs per chain was determined as 108 by 1H nuclear magnetic resonance analysis, which is equivalent to ∼27% coverage in length. The detailed synthesis procedure is given

elsewhere.23 SMALL-ANGLE NEUTRON SCATTERING CV-SANS measurements were performed on the SANS-U diffractometer of the Institute for Solid State Physics, the University of Tokyo, installed in

the neutron guide hall at the JRR-3 research reactor of the Japan Atomic Energy Agency in Tokai, Japan.24 Experiments were carried out at 4- and 1-m sample-to-detector lengths by using

neutrons of 7.0 Å wavelength with _Δλ_/_λ_=0.10 full-width at half-maximum, which covered the range of scattering wave numbers _Q_ from 0.01 Å−1 to 0.3 Å−1. The scattered neutrons were

detected by a two-dimensional multiwired 3He detector; thereafter, necessary data corrections such as dark counts (electronic noise and so on) subtraction and cell-scattering subtraction

were performed. After these corrections, the data sets were normalized to an absolute scale using the incoherent scattering of a polyethylene thin plate as a standard sample, and circular

averaging of the two-dimensional data and incoherent scattering subtraction proceeded. CONTRAST VARIATION EXPERIMENTS Contrast variation experiments were executed by preparing four solvents

with mixtures of hydrogenated and deuterated dimethylsulfoxide (h/d-DMSO), which consisted of 85, 90, 95 and 100 volume % d-DMSO. The corresponding scattering length densities were 4.46 ×

1010, 4.73 × 1010, 4.99 × 1010 and 5.25 × 1010 cm−2, respectively. In addition, two kinds of axial polymers were used, hydrogenated and deuterated PEG, as mentioned above, to improve the

reliability. In Figure 2, the scattering length densities of the components are summarized as a function of the volume fraction of d-DMSO in the solvent, _φ_d−DMSO. The scattering length

densities were estimated from the chemical structures and mass densities of the substances. Mass densities were measured using a DMA5000 density meter (Anton Paar, Graz, Austria) with sample

solutions at 25 °C: these densities were 1.14 g cm−3 for h-PEG, 1.59 g cm−3 for αCD and 1.10 g cm−3 for h-DMSO. The densities for deuterated materials were calculated by replacing protons

with deuteriums. The evaluated scattering length densities were 6.46 × 109 and 7.14 × 1010 cm−2 for h-PEG and d-PEG, respectively, and 1.97 × 1010 cm−2 for αCD. The volume fraction of PR in

all solutions was 8%. The temperature of the samples was regulated to be 25 °C by a water-circulating thermostat bath with an accuracy of ±0.1 °C. The decomposition of the intensities into

the partial scattering functions can be executed by _singular value decomposition_ for each _Q_ value by knowing each contrast as precisely as possible. The experimental and theoretical

details of the method are described elsewhere.25 RESULTS AND DISCUSSION Figure 3 shows the scattering intensities observed in the contrast variation experiments for the eight samples, the

structures of which were identical and scattering length densities of PEG and the solvents were different. Obvious characteristics of the curves are upward convexity for the samples with

h-PEG and downward convex for samples with d-PEG. This difference is because the sign of the cross-term Δ_ρ_c in Equation (11) is always negative under any experimental conditions, but

Δ_ρ__p_ is positive for d-PEG and negative for h-PEG as shown in Figure 2. In Equation (11), therefore, the contrast factor _S_CP(_Q_) becomes positive for h-PEG and negative for d-PEG,

which is the origin of the different shapes of the scattering intensities. From this observation, the sign of _S_CP(_Q_) can be estimated to be positive. The average intensity of each curve

decreases with the decreasing volume fraction of d-DMSO in the solvent, _φ_d−DMSO, which corresponds to a decrease in the scattering contrast between PR and the solvent with decreasing

_φ_d−DMSO. The obtained partial scattering functions of αCD, _S_CC(_Q_), PEG, _S_PP(_Q_) and αCD-PEG cross-term, _S_CP(_Q_), are shown in Figure 4a. As mentioned above, _S_CP(_Q_) is

positive and the magnitude is between _S_CC(_Q_) and _S_PP(_Q_), and the relation _S_CC(_Q_)>_S_CP(_Q_)>_S_PP(_Q_) is held. The average value of the square root of the ratio of

_S_CC(_Q_) to _S_PP(_Q_), which corresponds to the volume ratio between αCD and PEG in PR, is 2.9. The calculated ratio based on the nuclear magnetic resonance result is 2.1; thus, these

values roughly coincide, and the error may arise from the effect of the structure factor (intermolecular interaction). Furthermore, the _Q_-dependence of _S_CC(_Q_) is similar to that of

_S_PP(_Q_), which suggests that αCDs randomly distribute on the axial chain. The slopes at Q >0.1 Å−1 are clearly different; that is, the slope of _S_PP(_Q_) is more gradual than those of

_S_CP(_Q_) and _S_CC(_Q_). This is because _S_CP(_Q_) and _S_CC(_Q_) reflect the cylinder-like structure of the threaded αCD. These observations are consistent with the structure of PR;

that is, αCDs are mechanically interlocked by PEG. The reconstructed intensities are compared with the experimental values in Figure 4b, where the reconstructed intensities were calculated

from the obtained partial scattering functions and the evaluated scattering length densities from Equation (11). The reconstructed intensities reproduce the experimental results quite well,

which confirms the good reliability of the overall experimental procedures. To reveal the detailed structure of PR, the partial scattering functions were analyzed individually. Before the

fitting procedure, PR was identified to reduce as many uncertain parameters as possible with the other methods; for example, nuclear magnetic resonance, gel permeation chromatography (GPC),

density measurements and checking values in the literature. The fixed parameters are summarized in Table 1. At first, the persistence length _l_p of PR was determined. The best way to

determine _l_p is by analyzing _S_PP(_Q_), as _S_PP(_Q_) contains only information of the axial part of PR. Unfortunately, the statistical precision of _S_PP(_Q_) is not as good as that of

_S_CP(_Q_) and _S_CC(_Q_) because of a lack of contrast variation experiments in which the polymer is mainly visible. Therefore, _S_CP(_Q_) was analyzed with Equation (25), using Equation

(19) for the determination of _l_p, which is actually the second-best way. The fitting parameters for _S_CP(_Q_) were _l_p and the interaction term 2_A_2_Mc_ (see Equation (25)), and all of

the other parameters could be fixed; therefore, the two parameters could be fitted with high reliability. The determined _l_p from _S_CP(_Q_) is 23±2 Å. This value is rather large compared

with that of PEG, which is 11 Å under similar conditions.16 This unusually long persistence length is one of the characteristics of PR.13, 16 The origin of stiffness will be further

discussed below. The value was used for the fitting of _S_PP(_Q_) with Equation (12) and _S_CC(_Q_) with Equation (14), using Equation (25) for inclusion of the effect of intermolecular

interaction represented by 2_A_2_Mc_. In Figure 5, the partial scattering functions with the resulting fitting curves are shown. The curves can reproduce the experimental results fairly

well. The obtained parameters are summarized in Table 2. The second virial coefficients, _A_2, of each partial scattering function were separately obtained. For the calculation of _A_2 for

_S_CP(_Q_), and were applied, where _M_PEG/αCD and _c_PEG/αCD are the molecular weight and mass concentration of PEG/αCD, respectively. The obtained _A_2 for _S_CC(_Q_) is reasonably

comparable to the results in Mayumi _et al._16 On the other hand, _A_2 values for _S_CP(_Q_) and _S_PP(_Q_) are one order of magnitude larger than that of _S_CC(_Q_). The excluded volume _ν_

can be related to _A_2 through Equation (26); thus, _A_2 ∝ _ν_. Therefore, these relatively large _A_2 values compared with those of bare PEG may directly correspond to the large excluded

volume of PEG in PR because of the coating of αCD. All of the above analyses and subsequent discussions were based on the assumption that the distribution of αCD in PR is random. In other

words, no specific interaction among αCDs is assumed. Then, consistent results were obtained. To investigate the array of αCDs on the axial polymer in more detail, the conditional

probability that two αCDs are successively placed, _φ_cc, defined by Equations (21), (22), (23), was evaluated using Monte Carlo simulations, as explained in §2.5. In Figure 6, the fitting

results are exhibited, together with the fitting curve obtained by assuming a random distribution of αCDs. Sampling was repeated until the relative variation between the _n_th and (_n_+1)th

step became <10−2. Otherwise, the value was the average of 103 samplings. For the fitting procedure, the persistence length _l_p was fixed at 23 Å, preliminarily estimated by _S_CP(_Q_)

fitting; the evaluated parameters are listed in Table 2. No essential difference for the fitting curves was observed between the results assuming random or biased distribution, and

_φ_cc=0.25 was achieved, which is quite close to the average length fraction of αCDs, _Φ_, which is _Φ_=0.27. This result also supports the random distribution of αCDs in PR. Finally, we

discuss briefly the effect of the alignment of the cyclic molecules threaded with the axial polymer on conformation of PR. Let us assume that we have a polymer with contour length _L_ and

Kuhn length _b_. In this case, the statistical segment number _N_ may be defined as _N_=_L_/_b_. Ideally, the conformational entropy _S_p can be given on the basis of Gaussian statistics as

where with the Boltzmann constant _k_B and the length of the end-to-end vector _R_. Next, the effect of arrangement of the cyclic molecules is considered. The maximum number of cyclic

molecules in one molecule of PR is defined as _n_c, and the number fraction of the cyclic molecules in PR is defined as _φ_c. By assuming that the cyclic molecules distribute randomly in PR,

which is strongly supported by our analyses of the partial scattering functions, and that the cyclic molecules are prohibited from moving to the next segment, the number of alignments of

the cyclic molecules, _W_c, is given by The continuous description of Equation (29) is given by with Gamma function _Γ_(_x_) and the relation _x_!=_x_ × Γ(_x_). The total entropy, _S_T, is

then given by In Figure 7, _S_T, _S_p and _S_c are exhibited as functions of _N_ by fixing _n_c=400 and _φ_c=0.25, which are similar to the conditions of PR we used, assuming _R_/_L_ is very

small so that the exponential term in Equation (28) is approximately equal to unity. _S_p and _S_c have different _N_ dependencies: _S_p is a monotonically increasing function of _N_, and

_S_c is a monotonically decreasing function of _N_. As a result, the total entropy _S_T has a minimum. For increasing entropy to reduce the free energy, _N_ may approach 0, which is a

quasi-stable state, or increase beyond the minimum entropy, which is the stable state in this description. A decrease in _N_ corresponds to an enlargement of the persistence length, which is

the same as stiffening PR by purely entropic means. In this discussion, the elastic property of the polymer is missing, which normally limits the increase of _N_, so that the entropic

effect of the array of cyclic molecules may become important in the case that both _N_ and _φ_c are small. In the event that _φ_c becomes larger, the interaction between cyclic molecules

should become considerably important. CONCLUSIONS We investigated the static structure of PR in a good solvent by means of CV-SANS. The partial scattering functions of αCD, _S_CC(_Q_), PEG,

_S_CC(_Q_) and the cross-term between αCD-PEG, _S_CP(_Q_) were extracted by performing contrast variation experiments with high precision. Theoretical equations of each partial scattering

function were derived on the basis of the worm-like chain model by assuming a random distribution of αCDs threaded on PEG. This enabled us to evaluate the detailed structural properties of

PR in solution, such as persistence length of the axial polymer, alignment of αCD on the axis and intermolecular interaction with the quantitative comparison between experimental results and

the theory. Our results strongly support the idea that αCDs distribute randomly on PEG axial chains. The persistence length of PR determined from _S_CP(_Q_), which was 23 Å, and the second

virial coefficient for _S_CC(_Q_) were consistent with our former results.16 The other two second virial coefficients of PEG and the cross-correlation between αCD and PEG were also obtained,

which were one order of magnitude larger than that of _S_CC(_Q_). We conclude that this is because of the specific structure of PR; that is, PEG is coated randomly by αCD. The origin of the

relatively large persistence length of PR was discussed very qualitatively by considering the entropic contribution of the randomly distributing αCD, which behaves in a manner opposite to

that of conformational entropy. This entropic effect may be important for PR with a small inclusion of αCDs. Supramolecules are one of the highly promising candidates for the development of

future molecular devices, and this study has proved that CV-SANS is a unique and efficient tool to explore such complex structures consisting of multiple components with nanoscale

resolution. REFERENCES * Yamakawa, H. _Modern Theory of Polymer Solutions_ (Harper and Row, New York, 1971). Google Scholar  * Doi, M & Edwards, S. F _The Theory of Polymer Dynamics_

(Oxford University Press, Oxford, 1988). Google Scholar  * Yamakawa, H. _Helical Wormlike Chain in Polymer Solutions_ (Springer-Verlag, Berlin, 1997). Book  Google Scholar  * Kuhn, W. Über

die Gestalt fadenförmiger Moleküle in Losungen. _Kolloid-Z._ 68, 2–18 (1934). Article  CAS  Google Scholar  * Flory, P. J. The configuration of real polymer chains. _J. Chem. Phys._ 17,

303–310 (1949). Article  CAS  Google Scholar  * Yamakawa, H. & Fujii, M. Statistical mechanics of helical wormlike chains. I. Differential equations and moments. _J. Chem. Phys._ 64,

5222–5228 (1976). Article  CAS  Google Scholar  * Lehn, J. M. Supramolecular chemistry. _Science_ 260, 1762–1763 (1993). Article  CAS  Google Scholar  * Harada, A., Li, J. & Kamachi, M.

The molecular necklace: a rotaxane containing many threaded α-cyclodextrins. _Nature_ 356, 325–327 (1992). Article  CAS  Google Scholar  * Harada, A., Hashidzume, A., Yamaguchi, H. &

Takashima, Y. Polymeric rotaxanes. _Chem. Rev._ 109, 5974–6023 (2009). Article  CAS  Google Scholar  * Okumura, Y. & Ito, K. The polyrotaxane gel: a topological gel by figure-of-eight

cross-links. _Adv. Mater._ 13, 485–487 (2001). Article  CAS  Google Scholar  * Ito, K. Novel cross-linking concept of polymer network: synthesis, structure, and properties of slide-ring gels

with freely movable junctions. _Polym. J._ 39, 489–499 (2007). Article  CAS  Google Scholar  * Karino, T., Okumura, Y., Ito, K. & Shibayama, M. SANS studies on spatial inhomogeneities

of slide-ring gels. _Macromolecules_ 37, 6177–6182 (2004). Article  CAS  Google Scholar  * Fleury, G., Brochon, C., Schlatter, G., Bonnet, G., Lapp, A. & Hadziioannou, G. Synthesis and

characterization of high molecular weight polyrotaxanes: towards the control over a wide range of threaded a-cyclodextrins. _Soft Matter_ 1, 378–385 (2005). Article  CAS  Google Scholar  *

Jarroux, N., Guegan, P., Cheradame, H. & Auvray, L. High conversion synthesis of pyrene end functionalized polyrotaxane based on poly(ethylene oxide) and α-cyclodextrins. _J. Phys. Chem.

B_ 109, 23816–23822 (2005). Article  CAS  Google Scholar  * Travelet, C., Schlatter, G., Hebraud, P., Brochon, C., Lapp, A., Anokhin, D. V., Ivanov, D. A., Gaillard, C. & Hadziioannou,

G. Multiblock copolymer behaviour of α-CD/PEO-based polyrotaxanes: towards nano-cylinder self-organization of α-CDs. _Soft Matter_ 4, 1855–1860 (2008). Article  CAS  Google Scholar  *

Mayumi, K., Osaka, N., Endo, H., Yokoyama, H., Sakai, Y., Shibayama, M. & Ito, K. Concentration-induced conformational change in linear polymer threaded into cyclic molecules.

_Macromolecules_ 41, 6480–6485 (2008). Article  CAS  Google Scholar  * Mayumi, K., Endo, H., Osaka, N., Yokoyama, H., Nagao, M., Shibayama, M. & Ito, K. Mechanically interlocked

structure of polyrotaxane investigated by contrast variation small-angle neutron scattering. _Macromolecules_ 42, 6327–6329 (2009). Article  CAS  Google Scholar  * Kratky, O. & Porod, G.

Röntgenuntersuchung gelöster Fadenmoleküle. _Rec. Trav. Chim. Pays-Bas._ 68, 1106–1123 (1949). Article  CAS  Google Scholar  * Yoshizaki, T. & Yamakawa, H. Scattering functions of

wormlike and helical wormlike chains. _Macromolecules_ 13, 1518–1525 (1980). Article  CAS  Google Scholar  * Endo, H. & Shibayama, M. Static partial scattering functions for linear and

ring random copolymers. _Polym. J._ 42, 157–160 (2010). Article  CAS  Google Scholar  * Zimm, B. H. The scattering of light and the radial distribution function of high polymer solutions.

_J. Chem. Phys._ 16, 1093–1099 (1948). Article  CAS  Google Scholar  * Daoud, M., Cotton, P., Farnoux, B., Jannink, G., Sarma, G, Benoit, H., Duplessix, R., Picot, C. & de Gennes, P. G.

Solutions of flexible polymers. Neutron experiments and interpretation. _Macromolecules_ 8, 804–818 (1975). Article  CAS  Google Scholar  * Araki, J., Zhao, C. & Ito, K. Efficient

production of polyrotaxanes from a-cyclodextrin and poly(ethylene glycol). _Macromolecules_ 38, 7524–7527 (2005). Article  CAS  Google Scholar  * Okabe, S., Karino, T., Nagao, M., Watanabe,

S. & Shibayama, M. Current status of the 32 m small-angle neutron scattering instrument SANS-U. _Nucl. Instrum. Methods Phys. Res. A_ 572, 853–858 (2007). Article  CAS  Google Scholar  *

Endo, H., Schwahn, D. & Cölfen, H. On the role of block copolymer additives for calcium carbonate crystallization: small angle neutron scattering investigation by applying contrast

variation. _J. Chem. Phys._ 120, 9410–9423 (2004). Article  CAS  Google Scholar  Download references ACKNOWLEDGEMENTS This work was partially supported by the Ministry of Education, Science,

Sports and Culture, Japan (Grant-in-Aid for Scientific Research on Priority Areas, 2006–2010, No. 18068004 and Grant-in-Aid for Scientific Research (S), 2008–2012, No. 20221005). The SANS

experiment was performed with the approval of the Institute for Solid State Physics, The University of Tokyo, at the Japan Atomic Energy Agency, Tokai, Japan (Proposal No. 7607). AUTHOR

INFORMATION Author notes * Hitoshi Endo Present address: 3Current address: Neutron Biophysics Group, Quantum Beam Science Directorate, Japan Atomic Energy Agency, 2-4 Shirane, Shirakata,

Tokai-Mura, Ibaraki 319-1195, Japan., * Noboru Osaka Present address: 4Current address: Department of Organic and Polymer Materials Chemistry, Tokyo University of Agriculture and Technology,

2-24-16 Nakamachi, Koganei, Tokyo 184-8588, Japan., AUTHORS AND AFFILIATIONS * Neutron Science Laboratory, Institute for Solid State Physics, The University of Tokyo, Ibaraki, Japan Hitoshi

Endo, Noboru Osaka & Mitsuhiro Shibayama * Graduate School of Frontier Sciences, The University of Tokyo, Chiba, Japan Koichi Mayumi & Kohzo Ito Authors * Hitoshi Endo View author

publications You can also search for this author inPubMed Google Scholar * Koichi Mayumi View author publications You can also search for this author inPubMed Google Scholar * Noboru Osaka

View author publications You can also search for this author inPubMed Google Scholar * Kohzo Ito View author publications You can also search for this author inPubMed Google Scholar *

Mitsuhiro Shibayama View author publications You can also search for this author inPubMed Google Scholar CORRESPONDING AUTHORS Correspondence to Hitoshi Endo or Koichi Mayumi. APPENDIX A

APPENDIX A FORM FACTOR OF A DISCRETE ROD The scattering amplitude of a rod of length _L_ is given by where the classic coordinate system with the _z_ axis in the direction of the vector _Q_

(_Q·r_=_Qr_ cos_θ_) is used. Then, an analytical form of the form factor of the rod can be obtained: which is identical to Equation (5). We discretize Equation (A1) by assuming that the rod

consists of monomer-A and monomer-B, where the total number of monomers is _n_0 and the length of one monomer unit is _L_/_n_0. The discretization proceeds as follows: Therefore, the

corresponding form factor of a discrete rod composed of monomer-A is obtained by with the _n_0-dimensional vector _A__m/n_(_k_) defined by Equation (8). In the case of a purely random

process for the distribution of monomer-A, _A__m/n_(_k_) can be substituted by the ensemble average defined by Equation (9); then, an analytic form of Equation (A4) can be derived as where

_P_R(_x_)=2Si(_x_)/_x_−{sin(x)/x}2 with the sine integral Si(_x_). In the case of a discrete cylinder with base radius _R_ and length _L_, instead of the discrete rod, Equation (A4) is

modified as where _P_Disk(_x_)={2_J__1_(_x_)/_x_}2 with the first-order cylindrical Bessel function _J_1(_x_). For hollow cylindrical objects such as cyclic molecules, _P_Disk(_x_) can be

substituted by where _R_in is the internal radius and _R_out is the external radius. For the purely random process of the distribution of monomer-A, Equation (A6) can be reduced to RIGHTS

AND PERMISSIONS Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Endo, H., Mayumi, K., Osaka, N. _et al._ The static structure of polyrotaxane in solution investigated by

contrast variation small-angle neutron scattering. _Polym J_ 43, 155–163 (2011). https://doi.org/10.1038/pj.2010.124 Download citation * Received: 15 May 2010 * Revised: 21 October 2010 *

Accepted: 22 October 2010 * Published: 08 December 2010 * Issue Date: February 2011 * DOI: https://doi.org/10.1038/pj.2010.124 SHARE THIS ARTICLE Anyone you share the following link with

will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt

content-sharing initiative KEYWORDS * contrast variation * partial scattering function * polymer solution * polyrotaxane * small-angle neutron scattering * supramolecule