Simulated Apoptosis/Neurogenesis Regulates Learning and Memory Capabilities of Adaptive Neural Networks

Characterization of neuronal death and neurogenesis in the adult brain of birds, humans, and other mammals raises the possibility that neuronal turnover represents a special form of

neuroplasticity associated with stress responses, cognition, and the pathophysiology and treatment of psychiatric disorders. Multilayer neural network models capable of learning alphabetic

character representations via incremental synaptic connection strength changes were used to assess additional learning and memory effects incurred by simulation of coordinated apoptotic and

neurogenic events in the middle layer. Using a consistent incremental learning capability across all neurons and experimental conditions, increasing the number of middle layer neurons

undergoing turnover increased network learning capacity for new information, and increased forgetting of old information. Simulations also showed that specific patterns of neural turnover

based on individual neuronal connection characteristics, or the temporal-spatial pattern of neurons chosen for turnover during new learning impacts new learning performance. These

simulations predict that apoptotic and neurogenic events could act together to produce specific learning and memory effects beyond those provided by ongoing mechanisms of connection

plasticity in neuronal populations. Regulation of rates as well as patterns of neuronal turnover may serve an important function in tuning the informatic properties of plastic networks

according to novel informational demands. Analogous regulation in the hippocampus may provide for adaptive cognitive and emotional responses to novel and stressful contexts, or operate

suboptimally as a basis for psychiatric disorders. The implications of these elementary simulations for future biological and neural modeling research on apoptosis and neurogenesis are

discussed.

While it has long been accepted that neurons in the developing and adult brain die, it has only recently been widely recognized that new cells are also born in adulthood that develop

phenotypes and connectivity characteristic of mature neurons (Markakis and Gage, 1999; Gould et al, 2000). Adult neurogenesis occurs across mammalian species including mouse, rat, monkey,

humans, and others, appearing most robustly in certain brain regions, particularly the dentate gryrus (DG) of the hippocampus and in the olfactory system (Eriksson et al, 1998; Kornack and

Rakic, 2001). The idea that new neurons should positively impact cognition has generated significant interest especially in regard to the hippocampus since this structure is prominently

identified with short- and long-term memory (McClelland et al, 1995), local mechanisms of learning and memory such as long-term potentiation (LTP) and its variants (Wang et al, 1997), brain

adaptations to sex and stress hormones influencing pubertal neurodevelopment and stress responses (Garcia-Segura et al, 1994; McEwen, 2000), and various forms of mental illness including

major depression, post-traumatic stress disorder, and trauma-related personality disorders, and schizophrenia (Bremner et al, 1997; Duman et al, 2000; Eisch, 2002). Increased dentate granule

cell proliferation or survival is associated with increased cognitive performance, social interaction, environmental novelty, sex-steroids, antidepressant medications, and electroconvulsive

treatment (Duman et al, 1999; Gould et al, 2000; Kempermann and Gage, 2002), while decreases are associated with cognitive deficits, social isolation, physical or psychological stress, or

exposure to stress hormones (Duman et al, 2000; Gould et al, 2000; Shors et al, 2001).

Despite accumulating data, the functional significance of neuronal birth and death in the adult brain remains incompletely understood. Given data supporting that neuroadaptations among

permanent neuronal populations serve as a basis for cognitive and emotional learning, memory and behavior (Kandel et al, 1991), the added role or functional necessity of neurogenic events

remains unclear. Moreover, since molecular, neurochemical, pharmacological, and environmental factors identified with the control of apoptotic and/or neurogenic events also impact

traditionally recognized forms of neuroplasticity among permanent neural populations (Schwartz, 1992; Duman et al, 2000; Gould et al, 2000), the design of biological experiments capable of

defining or proving a unique role for neurogenic events in already plastic systems is daunting. Another uncertainty involves the possibility of functional associations of apoptotic and

neurogenic events (Biebl et al, 2000). Few studies have addressed whether the cognitive significance of neurogenesis can be fully understood without regard to a larger paradigm of neuronal

turnover in which both apoptotic and neurogenic events play important roles (Dong et al, 2003; Nottebohm, 2002).

By allowing direct investigation of the learning and memory characteristics of neural systems, neural network simulations are especially useful in understanding and contrasting the

functional significance of alternate forms of plasticity in a manner not easily observable with biological methods (Aakerlund and Hemmingsen, 1998). Network simulations may also represent an

important complimentary approach to direct biological investigations in examining the influence of apoptosis and neurogenesis on cognitive functions of neural systems. Simulations of the

olfactory system by Cecchi et al (2001) revealed that neurogenic events paired with apoptosis by competitive elimination can operate alone as an effective form of neuroplasticity allowing

efficient learning of new information. Building on these findings, we aimed to utilize elementary three-layer neural network simulations that are already capable of robust learning via

incremental neuronal connection plasticity, and to superimpose on these systems simulated apoptotic and neurogenic events in the middle layer. This approach allows comparisons of network

learning with and without various regimens of neuronal turnover. In choosing from among a large diversity of network architectures and functional attributes, we selected standard multilayer

feedforward pattern recognition networks because of their relative simplicity and wide usage, combined with a powerful and intuitively approachable learning capability (Widrow and Lehr,

1998). The simplicity of these networks, while sacrificing the added complexity needed to simulate more biologically accurate networks, offered the possibility of uncovering fundamental or

generic properties that may be generalized to other more complex systems.

We studied three-layer feedforward networks that learn to produce specific firing patterns in the output layer upon the introduction of topographically specific firing patterns in the input

layer (ie alphabetic letters). Learning of whole data sets (alphabets) occurs via a progression of incremental connection strength changes between neurons. With the storage of information,

the ‘maturation’ of individual neurons is observable as the quantifiable growth of axodendritic connection strengths from initial low random values.

Network simulations were used to test the hypothesis that neuronal turnover in information-bearing (‘adult’) networks produces greater performance in learning new information that can be

achieved by ongoing connection plasticity alone. Additionally, we tested whether alternate proportions or patterns of simulated apoptotic/neurogenic events may determine the extent of these

informatic effects. In modeling neuronal turnover in the ‘adult’ condition, we simulated various regimens of apoptosis–neurogenesis in networks after they had first accurately learned an

initial data set, the Roman alphabet. Networks were then tested on their performance in learning a new data set, the Greek alphabet. Under all learning conditions, the incremental weight

change learning algorithm was unaltered to simulate a consistent plastic potential among all neurons, whether mature or information-naïve. Neuronal turnover was modeled as the elimination of

information-laden individual neurons from the middle of the three-layer networks, and their replacement with new information-naïve neurons.

Networks were simulated utilizing MATLAB 6.0® mathematics software with MATLAB Neural Network Toolbox® performed on a PC-compatible Hewlett-Packard Pavilion N5445 (1 MHz) using Windows XP.

Network attributes including numbers of input, middle, and output layer neurons, neuronal input–output computational functions, learning algorithm, initial connection weight values, etc were

set prior to these experiments as recommended by accompanying software documentation (The MathWorks, Inc.) for character recognition learning.

Networks were organized as three-layer feedforward systems in which incremental connection plasticity occurs between the layers, but simulated apoptotic/neurogenic events occur only in the

middle layer. This architecture shares aspects with hippocampal organization where a non-neurogenic input layer (Entorhinal Cortex) projects to the neurogenic middle layer (DG) via

modifiable perforant path axodendritic connections, and DG projects to non-neurogenic CA3 neurons via modifiable mossy fiber axodendritic connections. The simulated input layer comprised 35

neurons fully connected to the middle layer via an array of 35 × 10 axodendritic connections labeled collectively as I–M (input to middle). In turn, 10 middle layer neurons are fully

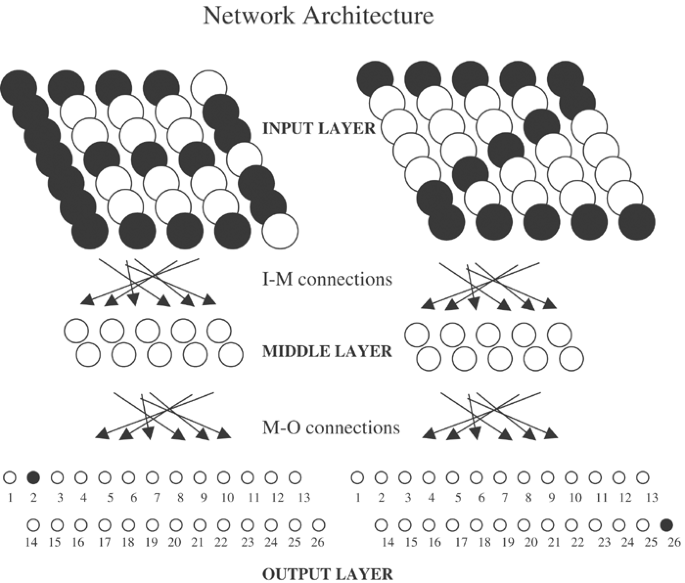
connected to 35 output layer neurons via the M–O (middle to output) axodendritic system. With this architecture (Figure 1), network learning allows topographically arranged neuronal firing

rates of 1 or 0 forming alphabetic letter representations in the input layer (eg ‘B’ or ‘Z’) to produce desired output firing patterns in the output layer (eg fire neuron #2 only or #26

only).

Multilayer feedforward network architecture designed for learning pattern recognition of alphabetic characters are used to study informatic effects of neuronal turnover in the middle layer.

Desired input–output associations of the letters ‘B’ and ‘Z’ from the Roman alphabet are shown. Darkened circles represent neuronal firing rates of 1, while clear circles represent neurons

firing at or near zero.

Analogous to biological neurons, firing of simulated middle and ouput layer neurons is determined first by a summation of input signals from neurons in the previous layer. Each of these

input signals is multiplied by an axodendritic connection weight (w), serving as the computational equivalent of synaptic strength and the critical variable of change during incremental

learning (Figure 2). Summed input information plus a variable bias weight value is then processed by the neuronal input/output transformation function (MATLAB code: ‘logsig’). This

continuous sigmoidal function serves as the computational equivalent of somatodendritic activation of action potentials whereby neuronal firing ranges between 0 (no firing) and 1 (maximal

firing).

Models of individual neurons used in simulated networks. Network input takes the form of values of one or zero presented to individual input layer (IL) neurons and relayed to each of 10

middle layer (ML) neurons via I–M connections. Each middle layer neuron receives an input signal from all 35 input neurons, each of which are multiplied by a connection weight (w) value. A

dendritio-somatic input signal is calculated as the sum of these products plus a bias weight (wb), and is acted upon by an input/output transformation function to produce a middle layer

neuronal output signal. Ouput layer neurons follow a similar design to produce final network output. Incremental changes in connection and bias weights of associated with middle and output

layer neurons mediate network learning.

Before learning, the axodendritic connection weight (w) values of networks are set as low random values ranging between −1 and 1 in the case of I–M connections (MATLAB code: ‘rands’) and

between −0.01 and 0.01 for the M–O connections. These values have previously been established as maximally optimal for learning character recognition in three-layer systems. The much smaller

initial absolute magnitudes of the M–O compared to I–M connections may be considered as reflecting connection states particular to immature, information-naïve neurons where efferent axonal

projections are considerably more underdeveloped compared to afferent axodendritc connections from the previous layer.

Axodendritic connection weight changes during learning in all experiments were determined by gradient descent backpropagation, with variable learning rate (MATLAB code: trainFcn=‘traingda’).

In this algorithm, specified (to be learned) input patterns generate an actual output pattern that is mathematically compared with the desired (to be learned) output patterns, producing an

error quantity. As described elsewhere (Widrow and Lehr, 1998), methods of differential equations are used to determine how small changes in I–M and M–O connection weights can be made to

minimize the error quantity (error gradient descent). One epoch of training consists of one exposure to a set of input patterns (ie the Roman alphabet), corresponding to incremental changes

in connection weights. Use of the variable learning rates option allows the size of the incremental weight changes to vary slightly between epochs depending on the slope of the error

gradient, enhancing learning efficiency.

The chosen data sets were designed according to development theories that new learning involves elaboration of old information (Yates, 1996). The initial training set comprised the set of

input and output representations of 26 letters of the Roman alphabet. Figure 3 shows the topographical configurations of firing patterns of input neurons and the desired output neuron to

fire, corresponding to each letter of the alphabetic data set. The second training set (24 letters of the Greek alphabet) was chosen to be of similar size and complexity as the first

training set, but with some noticeable differences (eg some new characters, fewer number of total characters, new input–output configurations).

Input–Output patterns of the alphabetic data sets. Networks are taught to associate input representations of Roman alphabetic characters presented to the input layer with output patterns

represented in the output layer. Character inputs are topographical arrangements of 1 s (black) and 0 s (white) at each of 35 neurons in the input layer. Output numbers represent the

specified output neuron(s) that activate(s) (fires close to a value of 1) while all others fire at rates close to 0, upon presentation of a given character.

Neuronal turnover was modeled as the removal of a variable number of middle layer neurons and their replacement with information-naïve neurons, maintaining a constant number of middle

neurons at 10. Nascent middle layer neurons were architecturally similar to the neurons they replaced in terms of complete connectivity with input and ouput layers, except their connection

weight (w) values were now rerandomized to low values (between −1 and 1 for I–M connections, between −0.01 and 0.01 for M–O connections). Thus neurogenic middle layer neurons were defined by

immature connectivity states, as was the case for all network neurons before initial learning of the Roman alphabet. Information bearing connections of permanent output layer and mature

middle layer neurons not selected for turnover were left unaltered.

Network memory performance was measured as a quantitative comparison of information recall after learning (actual firing rates of output neurons, given presentation of alphabetic letters to

input layer), with the information on which the net was trained (desired firing rates of output neurons, specified by alphabetic letters), summed over all the letters of a given alphabet.

This quantity, sum of the squared errors (SSE) is defined

Lower SSE values indicate improved memory performance. Learning performance plots SSE with respect to the number of epochs of training and improves when networks require fewer epochs of

training to achieve lower SSEs.

Computations governing input–output activity and the learning procedures were fully deterministic and did not represent a source of variation. Other than experimental effects, some variation

in performance was introduced from the low randomized initialization values assigned to neuronal connection weights in information-naïve networks or neurogenerated neurons. Assignment of

these low, random values optimizes learning potential of information-naïve networks and is analogous to genetic sources of variation in biological studies since they are set prior to

environmental exposure (information learning). To control for this source of genetic-like variation, studies were conducted on groups composed of eight networks first individualized by

virtue of their separately randomized initial weight configurations, and then trained on the Roman alphabet (Figure 4). Experimental groups were then created according to the particular

condition of neuronal turnover imposed on the original group of eight networks. Two-tailed Student's t-tests or ANOVA procedures were used to compare the effects of two or more conditions of

neuronal turnover on memory performance. Repeated measures ANOVA were used for group comparisons of learning performance followed by the post hoc Tukey procedure where applicable. Results

were considered significant at the p=0.05 level.

General experimental design. Eight individualized immature networks, defined by low random connection weight values modeling nascent, information-naïve neurons, undergo the standard

incremental training algorithm to learn the Roman alphabet. These networks are then replicated multiple times and sorted into identical groups exposed to unique conditions of neuronal

turnover and new learning of the Greek alphabet.

Eight individualized ‘immature’ networks were trained on the Roman alphabet to a level of recall performance of SSE=0.01, requiring a group mean of 517±24.9 epochs of training. Each of the

eight nets were then replicated and sorted into five identical groups treated under one of five conditions of apoptosis–neurogenesis where 1, 2, 5, 8, and 10 (all) middle layer neurons

underwent turnover, followed by training on the Greek alphabet. As demonstrated in Figure 5, initial training on Roman was associated with distributed patterns of connection weight growth.

Upon subsequent neuronal turnover and training on the second alphabet (Greek), connection weights of neurogenic middle layer neurons showed similar connection growth, while permanently

intact neurons showed various degrees of connection weight revision.

Serial Hinton graphs of a typical network reveal axodendritic weight changes in middle to output layer connections during learning. Individual Connection weights values are proportional to

the block sizes plotted according to their neuron of origin in the middle layer (x-axis) and connection to neuron in the ouput layer (y-axis). Colors indicate valence of connection weights

(red=negative, green=positive). Connection weights of information-naïve networks, initially too small for graphical representation here, undergo growth that allows storage of the entire

Roman alphabet with high accuracy by 461 epochs. After learning Roman and challenged with new learning of the Greek alphabet, connections undergo further adaptation. Without

‘apoptosis–neurogenesis’, connection changes are subtle by 100 epochs and become more pronounced by 2800 epochs when the network achieves mediocre recall accuracy of Greek (SSE=6.0).

Alternatively, with apoptosis–neurogenesis of middle layer neurons 1–5, implementation of the same incremental learning algorithm drives the axodendritic growth of new neurons into mature

configurations, allowing for improved recall of the new alphabet by 2800 epochs (SSE=3.0).

The results of increasing turnover on recall performance of old information (Roman) before learning the new information (Greek), and learning performance upon training on Greek are shown in

Figure 6. Increasing the number of neurons undergoing turnover generally increased degradation of memory of the Roman alphabet (Figure 6a): with no neurons, SSE=0.1±0.0; 2 neurons,

SSE=17.77±1.60; 5 neurons, SSE=48.32±3.23; 8 neurons, SSE=71.01±5.03, and all 10 neurons SSE=47.85±1.83 (group differences, F4,35=94.07, p